基于冗余测量的空间机械臂关节扭矩传感器研究*

孙玉香,许玉云,曹会彬*,双 丰,高理富,葛运建

(1.中国科学院合肥智能机械研究所仿生感知与先进机器人技术安徽省重点实验室,合肥 230031;2.中国科学技术大学自动化系,合肥 230026)

随着空间站在轨服务、深空探测等空间技术的迅速发展,对空间机械臂技术需求越来越迫切,空间机械臂的智能化可以更好地帮助其完成辅助对接、目标搬运和在轨建设等作业任务。力传感器作为空间机械臂智能化的关键部件之一,安装在机械臂的关节处,可帮助空间机械臂末端实现灵活控制[1-2]。

航天器发射阶段是外载荷最复杂,环境最恶劣,振动最强烈的阶段,是航天动力学环境研究的重点。此时安装在机械臂上的力/力矩传感器在这种强振动下容易发生高倍超载,导致传感器弹性体发生部分或者完全塑性形变,致使传感器损坏[3-4];再者航天器进入太空以后,面临高真空度、高低温交错以及电磁辐射等复杂的外部环境,这些外部环境会影响传感器的测量精度,甚至会损坏传感器。普通地面使用工业级的多维力传感器已经不适合在这样的环境中工作,为了保证空间力矩传感器使用的可靠性,必须研制新的传感器满足航天环境下的使用需求[5-6]。发达国家已经有空间力/力矩传感器成功应用的先例,但是对我国处在技术保密阶段;国内关于力/力矩传感器真正应用到空间机械臂上的鲜有报道,大多处在地面试验研究阶段,但是针对航天特殊环境应用的研究做了大量的工作[6-12],这些研究工作为力/力矩传感器在空间机械臂上的成功应用提供了基础。

扭矩传感器和机械臂关节零件进行一体化设计,可以实现空间机械臂高集成度,轻量化和高可靠的目标。本文为了满足空间机械臂扭矩传感器高抗过载和具备容错能力的使用需求,以空间机械臂关节输出法兰为设计原型,研制了一款一体化的关节扭矩传感器,该传感器采用八根弹性梁均匀地沿圆周方向分布的圆环结构。为了提高传感器高抗过载下的性能,对传感器弹性体进行受力分析,建立传感器扭转刚度和应变的解析模型,根据实际需求对传感器弹性体结构进行优化;为了提高传感器的容错能力,采用双路全桥冗余设计的方法,最后通过实验标定的方法验证了传感器的性能。

1 传感器结构设计及分析

1.1 传感器总体结构设计

关节输出法兰处于空间机械臂转动关节处,具体位置如图1所示。

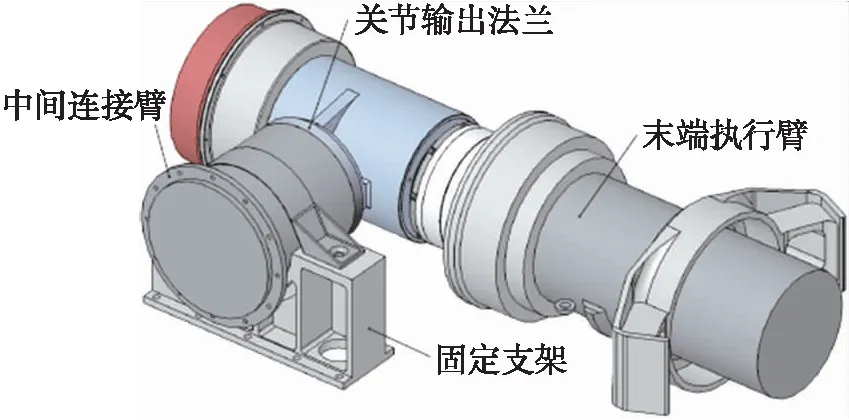
图1 空间机械臂部分模型

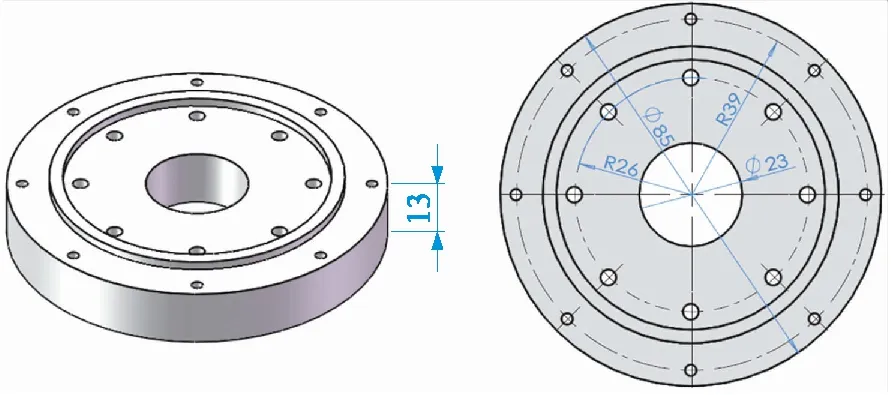
图2 关节输出法兰模型与尺寸图

关节输出法兰零件结构如图2所示,由于要在原关节法兰零件上设计弹性单元,并保持原有零件的内外固定接口的位置不变,要求在外径85 mm、内径23 mm和高度13 mm的区域范围内设计最大量程为50 N·m的扭力测量传感器,电路板要求安装在传感器内部,与此同时传感器要有5倍的过载能力(即传感器承受最大载荷250 N·m不被破坏,载荷释放后,传感器仍可正常使用),最小分辨力矩为0.1 N·m,扭转刚度要求大于4.5×105(N·m)/rad。

根据关节输出法兰的尺寸和安装位置的限制,结合传感器载荷需求,对传感器进行结构设计,详细结构如图3所示。该扭矩传感器主要有3个部分构成:加载环,矩形弹性梁组和固定环,8个弹性梁均匀地分布在加载环和固定环之间,每个弹性梁尺寸相同;弹性梁受载时,最大变形靠近连接固定环的一端,此处为应变片的粘贴地方;为方便采集全桥输出信号,将电路板安装在固定环上,电路板形状为圆环形。

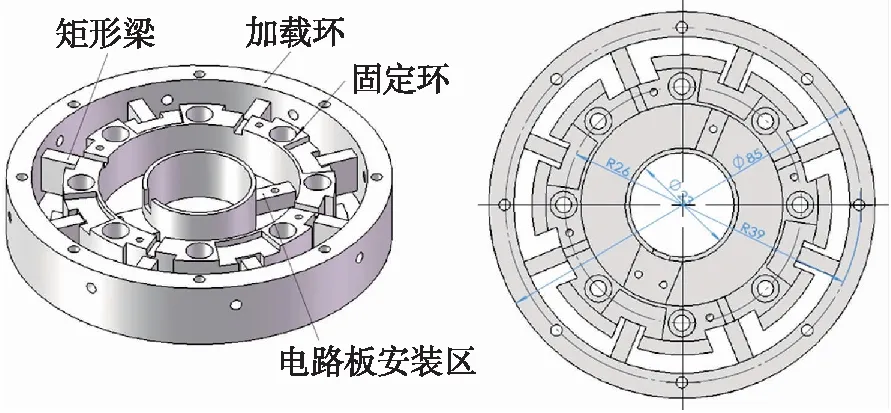
图3 传感器结构与尺寸图

1.2 弹性体受力分析

对传感器进行受力分析,建立传感器的解析模型,揭示载荷、结构与变形之间的本质关系,给传感器结构优化提供方向。

传感器变形主要集中在弹性梁上,加载环和固定环变形很小忽略不计,对传感器结构进行简化,简化后的模型如图4所示,图中传感器最大外径为ro,总体高度为H;矩形梁的尺寸长为a,宽为b,厚为h;固定环的内径为ri,固定环外为径r。

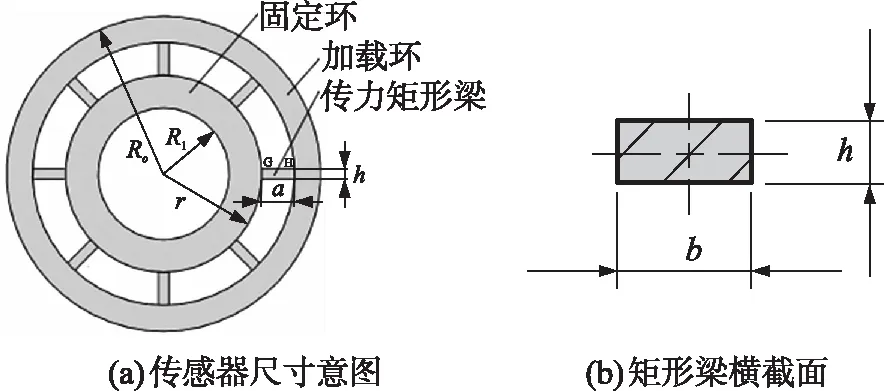
图4 传感器结构简化模型

给传感器加载环施加Mz扭转载荷时,取加载环为研究对象,加载环除了受到Mz的作用,还受到所有八根弹性梁的反作用力;由传感器的结构特点可知每个弹性梁在加载环上的反作用力大小相等,形变相同。以其中一个弹性梁与之接触点为例,取加载环为研究对象,建立受力模型如图5所示。

图5中,F11、F12和M11为单个弹性梁的反作用力,且满足力矩平衡方程:

F11(r+a)+M11=Mz/8

(1)

式中:r为固定环外径;a为弹性梁长度。

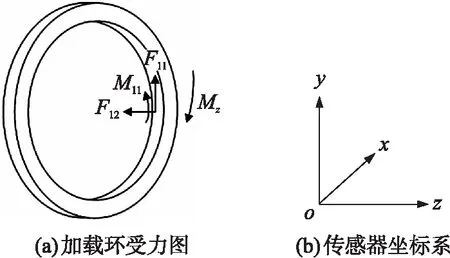
图5 传力环受力分析

以其中任一弹性梁为研究对象,将该梁标记为G、H,建立其受力模型如图6所示。

图6 弹性梁受力模型

(1)弹性梁的弯曲变形

(a)在F11作用下矩形梁的弯曲变形为:

(2)

式中:E为传感器材料的弹性模量;b为弹性梁截面的宽度,h为弹性梁截面的厚度。

由边界条件可知:

(3)

式中:I为弹性梁截面对水平中性轴的惯性矩,I=bh3/12。

(b)在M11作用下弹性梁的弯曲变形为

(4)

(5)

(2)弹性梁的拉压变形

在F12作用下弹性梁G、H的拉压变形为

(6)

式中:A为矩形弹性梁的横截面积,A=bh。

弹性梁G、H在F11和M11共同作用下H端截面的转角为:

(7)

(3)变形协调

加载环在单独力矩Mz作用下产生转角φMZ,根据载荷与结构特点可知:

φMZ=θ

(8)

即:

(9)

加载环转动φMZ的角度,加载环H点在Y轴方向产生位移如下:

Δy≈φMZ(r+a)

(10)

以加载环坐标系为参考坐标系,考虑Y轴方向的变形协调方程。

根据上述分析可知,Y轴方向变形主要是弹性梁G、H在F11和M11共同作用下产生的弯曲变形,即:

(11)

联立(1)和(11)求解得:

(12)

(13)

传感器在Mz作用下,传感器的扭转刚度和矩形梁的应变分别如下:

(14)

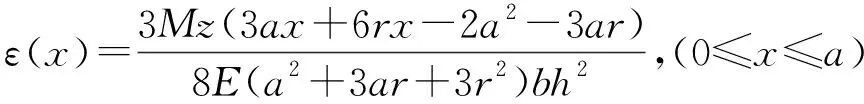
(15)

1.4 传感器结构优化

1.4.1 确定优化目标

灵敏度是评价传感器性能好环的重要指标之一,在满足使用条件下,灵敏度越高越好,灵敏度与传感器的结构尺寸相关,通过优化传感器的结构可以提高传感器的灵敏度[8]。

灵敏度定义为:

(16)

式中:ΔU为全桥输出电压,单位mV;U为传感器激励电压,单位V;K1为应变片灵敏系数;εT为真实应变。全桥电路输出电压为:

(17)

式中:ε1、ε2、ε3、ε4为全桥中应变片的应变,负号表示负方向应变。

将式(17)代入式(16)中,可得:

(18)

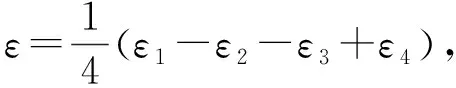
由于MATLAB优化工具箱函数fmincon,优化时要求目标函数趋于最小值,取f=1/S,K1=2将式(15)代入式(18),可得:

(19)

式中:x为应变片的粘贴位置。

1.4.2 变形约束条件

(1)测量最小应变条件

传感器最大量程为Mz,最小分辨力为t,同时由于实际工艺水平,粘贴位置误差等,实际设计时可取理论计算最小值的1.5倍,为满足使用需求,最大量程最小应变:

(20)

式中:UA/D为A/D最大采集电压,单位mV;U为传感器激励电压,单位V;Mz为传感器最大量程;t为传感器最小分辨力;n为电路放大倍数;N为A/D采集的位数。

根据空间机械臂对传感器的需求,A/D采集的位数为N=12位,UA/D=5 000 mV,激励电压U=5 V,电路放大倍数n=250,传感器最大量程为Mz=50 N·m,最小分辨力为t=0.1 N·m,应变片灵敏系数K1=2,代入式(20)可得:

(2)安全最大应变条件

传感器最大应变与传感器材料需用安全系数有关,安全系数为e,又因为本文设计的传感器在经历5倍过载以后,传感器依然可以正常使用,则传感器的最大应变:

(21)

式中:[ε]为保证材料弹性变形的最大应变极限;e为安全因数;p为传感器最大量程过载倍数。

在满量程载荷下,传感器弹性梁的形变在500 μm/m～1 000 μm/m之间具有良好的测量性能。本文要求传感器在承受5倍的满量程载荷后仍可正常使用,即弹性体在250 N·m载荷下依然处在弹性变形范围内,弹性梁形变范围为2 500 μm/m～5 000 μm/m,结合传感器的使用环境,本传感器加工材料采用强度大、弹性极限高,具有良好的综合力学性能TC4,材料的性能参数见表1。

表1 材料性能参数

由于在一般的机械制造中,在静载的情况下,对塑性材料的安全因素取es=1.2～2.5,本文取e=1.5,p=5,由表1可知TC4钛合金材料[ε]为8 454,代入式(21)则:

1.4.3 结构参数设计

在确定的已知参数下,结合扭矩传感器的安装尺寸、贴片尺寸和使用空间等需求,传感器优化范围确定如下:

(22)

以a,b,h,r为变量,以f(x=0.05)最小为优化目标函数,传感器结构优化后的的尺寸见表2。

表2 传感器结构尺寸 单位:mm

1.4.4 有限元仿真

有限元分析软件是检验弹性体结构设计是否合理的一种方法,本文采用ANSYS Workbench软件对弹性体结构进行应变分析,判断弹性体结构是否满足工作要求并找出最佳贴片位置。

首先用Solidwork对传感器弹性体进行三维建模,然后将其导入ANSYS Workbench进行有限元分析。

给传感器施加50 N·m的扭矩,传感器沿各个方向的应变如图7所示,由图7可知每根梁形变大小一致且梁的最大形变位置均靠近连接固定环的一端,将此位置作为应变片的粘贴位置;最大应变为506 μm/m,满足传感器应变优化范围。

图7 Mz=50 N·m时,传感器的应变情况

3 传感器电路设计

扭矩传感器在太空发生故障很难修复,为了提高传感器容错性,结合传感器使用需求,我对传感器进行了双全桥电路冗余设计,即单维扭矩传感器拥有两个测量电路,这样做的优势一方面提高了传感器的容错性能,另一方面利用信息冗余提高传感器的精度,每路采用惠斯通全桥设计,具体设计方式如图8所示。

图8 电路设计

图9 贴片示意图

R1、R2、R3和R4为一组测量电路,R5、R6、R7和R8为另外一组测量电路;R1和R2粘贴在一个梁的两侧,R3和R4贴在另外一根梁的两侧,这两个粘贴应变片的弹性梁沿轴心180°对称,另外一路粘贴方式与此相同,两路相互垂直,应变片在传感器上具体粘贴方式如图9所示,电路板与弹性体如图10所示。

图10 电路板与弹性体

4 传感器标定

4.1 标定方法

传感器的标定是其使用之前的重要工作,是建立力矩和电压之间数学模型的重要依据,严谨的标定过程有助于传感器性能的提高。传感器通过标定帽安装到标定台上(图11),对传感器的每个方向都进行拉伸标定,标定示意图如图12所示。

图12 标定方法示意图

图11 传感器标定安装图

其标定过程如下所述:以图12(a)为例,对P1、P2两个点分别施加大小相等,方向相反的力F1和F2,F1和F2通过钢丝绳加载砝码实现。首先待砝码挂盘平稳后软件取零;然后将F1和F2加载至传感器额定满量程并卸载,待数据稳定后记录数值,重复3次;图12(b)～图12(d)标定步骤与图12(a)的标定方法一致。

4.2 标定结果

(1)线性度分析

以加载的力矩为水平轴,以加载对应的输出电压为垂直轴,将传感器标定的数据在MATLAB里进行最小二乘法线性拟合,得到拟合后的直线如图13所示。得到电桥1、电桥2以及二者的冗余拟合直线如下:

y1-road=19.79x+2 467.81

y2-road=17.96x+2 499.26

yaverage=18.88x+2 483.54

经过计算,它们的最大线性度误差分别为1.81%,1.73%和0.77%,重复性误差分别为1.14%,1.06%和0.89%,迟滞误差分别为1.24%,1.15%和0.95%,通过上面数据可知(表3),通过桥路信息冗余处理有利于降低传感器的线性度误差、重复性误差和迟滞误差。

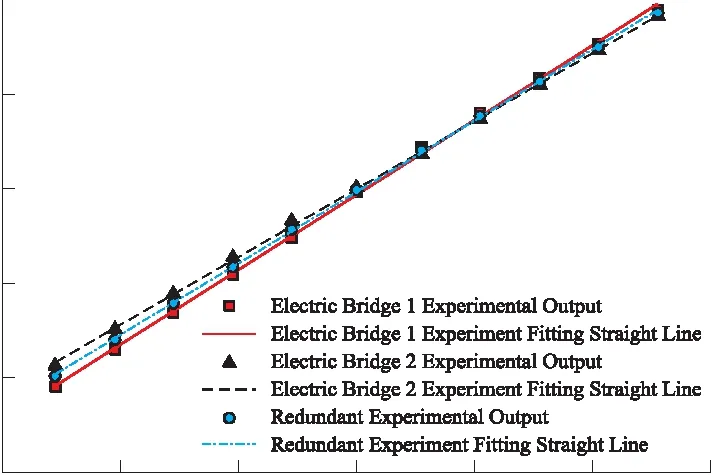
图13 标定结果线性拟合

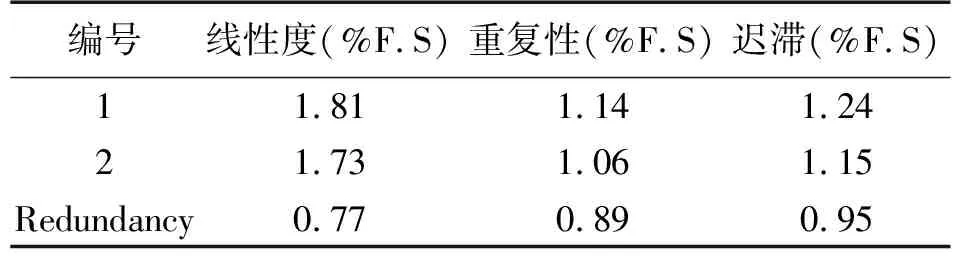
表3 传感器性能参数

(2)抗干扰能力分析

受到工作环境的影响,扭矩传感安装在机械臂上工作时会有Fz的干扰,针对这个问题,我们标定的时候,在Fz方向加载了固定干扰时,对传感器进行标定实验,实验结果如下:

图14显示的是传感器在轴向Fz=100 N和Fz=200 N干扰下传感器经冗余处理后拟直线合情况,其表达式如下:

yFz=0=18.88x+2 483.54

yFz=100 N=18.89x+2 481.93

yFz=200 N=18.89x+2 481.20

图14(a)显示的是没有进行冗余处理之前各路受Fz干扰的输出情况,图14(b)显示的是经过冗余处理以后,传感器的输出线性拟合情况,通过比较可以发现,在有Fz向干扰的情况下,它们的线性拟合直线的结果接近,Fz干扰对传感器扭矩测量影响较小。

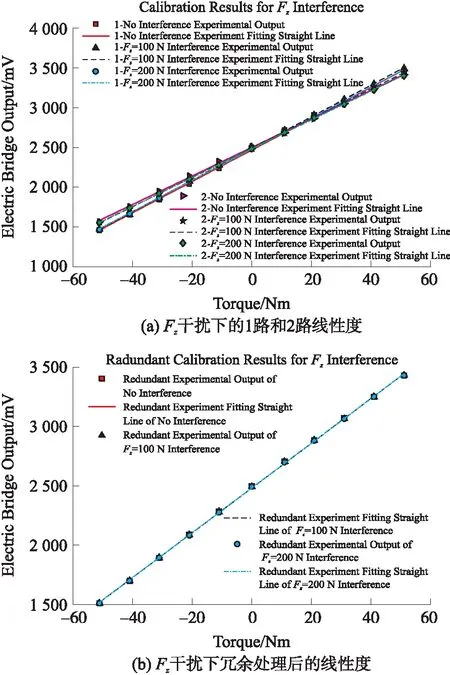
图14 Fz干扰线性度情况

5 结论

本文利用关节输出法兰设计了一款用于空间机械臂的扭矩传感器,建立传感器的扭转刚度和应变的解析模型,结合传感器载荷特点确定了优化范围和目标,对扭矩传感器的结构进行了优化,对传感器电路采用双桥冗余测量方法,经实验标定,经过冗余设计,传感器线性度得到改善,轴向抗干扰能力得到提高,线性度为0.77%;重复性0.89%;滞后为0.95%,满足航天传感器量程大,体积小,抗过载能力强和具有容错能力的特殊需求。