热释电传感器声功率测量的机理研究*

陈 倩,曹永刚,王月兵

(中国计量大学计量测试工程学院,浙江 杭州 310018)

早在2400多年前,热释电现象就已经被人们所发现[1]。但直至19世纪末,热释电效应的理论研究才逐渐被提出。研究表明热释电材料也是一种压电材料,主要集中于单晶、陶瓷及高分子聚合物中[2-3]。其中,热释电单晶材料的居里温度较高,但热释电系数较小;热释电陶瓷材料的制备工艺相对简单且成本较低,但不便于获得自发极化的薄膜;热释电聚合物材料聚偏氟乙烯(PVDF),是19世纪60年代被发现的,其最大优点是薄膜的形状和大小几乎不受工艺条件的限制。

PVDF薄膜制作的传感器中,最常用的是用于超声检测的PVDF压电换能器。另一种是PVDF热释电传感器,它除了形状大小不受限制外,还具有响应快、灵敏度高、制备方便等特点。目前,PVDF热释电传感器已经被广泛应用于多点监控与无线警报、红外传感等领域[4-6];在声学领域,超声功率的准确测量对评估诊疗设备的稳定性及安全性具有重要意义。Zeqiri B等人于2007年率先研制了一种用以检测诊断级超声功率的新型PVDF热释电传感器,通过超声激励成功获得了热释电信号,并对该传感器的热释电性能做了研究,研究表明此方法可被作为第二种标准方法用于声功率测量[7]。

虽然新型PVDF热释电传感器在声功率测量方面显现出了巨大潜力,但目前尚未对传感器声功率测量的机理进行深入研究。因此,本文将围绕超声波与热释电信号的转换机制展开研究。介绍该传感器的基本结构并通过理论计算研究了声传感机理,利用有限元分析法建立了物理模型,运用仿真程序对传感器内部声场分布及薄膜表面温升进行了仿真计算并预测了热释电信号波形及幅值大小。同时,根据仿真结果设计及制备了传感器并搭建了实验测试系统,并对传感器时域及幅值特性进行检测和分析,对PVDF热释电传感器测量声功率的可行性、理论模型的准确性进行了证明。

1 声传感机理

图1为PVDF热释电传感器测量声功率的原理简图。热释电传感器与传统的压电水听器结构类似[8],其最大的特点是选用了高阻尼的复合材料作为背衬,接收的超声信号会在背衬材料较高的粘滞阻力作用下,迅速衰减转化为热能。测量时,聚焦换能器作为声源辐射超声波,并在介质中形成聚焦声场。将PVDF热释电传感器的表面,放置于声场焦域附近。由于PVDF薄膜的声阻抗与水接近,绝大部分的声波将透过薄膜,透射到背衬材料内部,再衰减为热能。伴随着热传递作用,背衬升温将导致PVDF薄膜的温变,利用PVDF的热释电效应进而在传感器的输出端产生热释电信号。

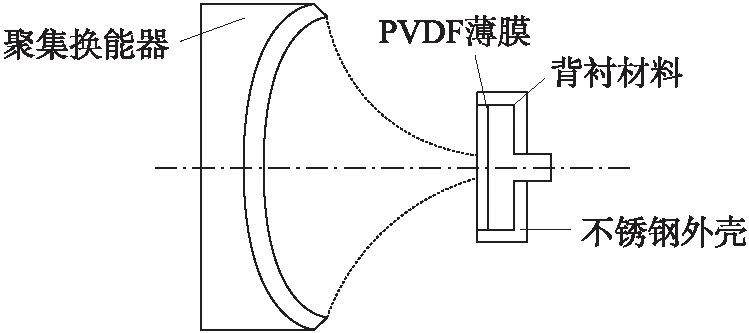
图1 PVDF热释电传感器声功率测量简图

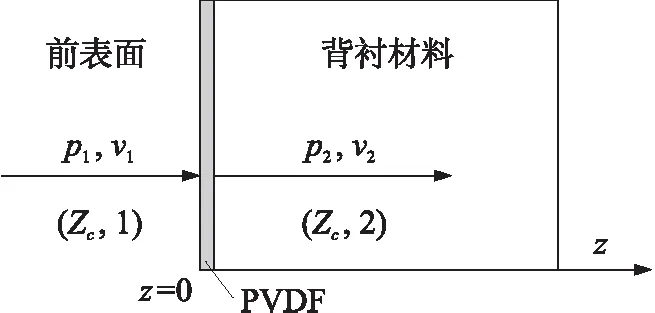
图2 声波穿过PVDF至背衬材料示意图

1.1 超声波的传播

基于波动方程理论,对超声波在介质及传感器内的传播特性进行分析。通常情况下,将聚焦声场焦域内声波近似看作平面波,因此超声波在PVDF热释电传感器表面的传播过程可近似看作垂直入射的过程,从而忽略声波在传感器内部由纵波到横波的转化;此外,传感器中PVDF的厚度仅为a=50.0 μm,a≤λ=2.3 mm(λ为超声波波长),因此可忽略PVDF薄膜对声波的反射、透射和声吸收作用,声波的传递过程可简化如图2所示。

声波在传感器前表面及背衬材料内部(z=d,深度为d)的声压和质点振速分别为p1、p2和v1,v2,根据波动方程,p1,v1表示如下:

p1(z,t)=piaej(ϖt-k1z)+praej(ϖt+k1z)

(1)

(2)

式中:媒质波数k=ϖ/c,ω为角频率,c为声传播速度,pia为入射波幅值,pra为反射波幅值,ZC,1=ρ1c1为传感器前表面媒质的特性声阻抗。

现用传递矩阵来描述传感器前表面与背衬材料内部的状态变量关系(声压和质点振速)的关系,可得p2,v2如下所示[9]:

(3)

式中:背衬材料中的波数k=ϖ/c-jα,α为背衬材料的衰减系数,d为背衬材料内部的一点距前表面的深度,ZC,2=ρ2c2表示传感器内部背衬材料特性声阻抗,ρ2c2分别表示背衬材料的密度及声速。

根据式(3)求得传感器内任意位置的状态变量,进一步可得传感器内任意位置声强向量,具体表述如下:

(4)

1.2 传感器内部温升效应

超声波被背衬材料吸收的过程,就是机械能转换为热能导致材料升温的过程。根据传热方程可获得背衬材料内部某一点处的温变速率,具体表示如下[10]:

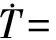
(5)

在声学介质中,qv由声强向量的散度组成。而声波作为平面波在Z轴方向传播,在传感器内部产生的单位体积热qv具体表示如下[11]:

(6)

式中:αbacking表示背衬材料的衰减系数,Iincident和Ireflected分别表示入射与反射声强向量。

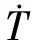
(7)

由于热释电传感器为圆柱形,因此可将上述问题简化成轴对称问题,Z轴上温度上升可通过下式表示:

(8)

式中:K表示材料的热传导系数,ε表示热源厚度,d表示热源直径,r表示薄膜与热源的距离。

1.3 PVDF热释电效应

传感器内部背衬温升由于热传导将背衬温度体变化传递至PVDF薄膜表面,基于PVDF的热释电效应,热能转换成电能。在此过程中,将PVDF薄膜等效为一电流源、电容与电阻并联的关系,等效电路如图3所示[12]。

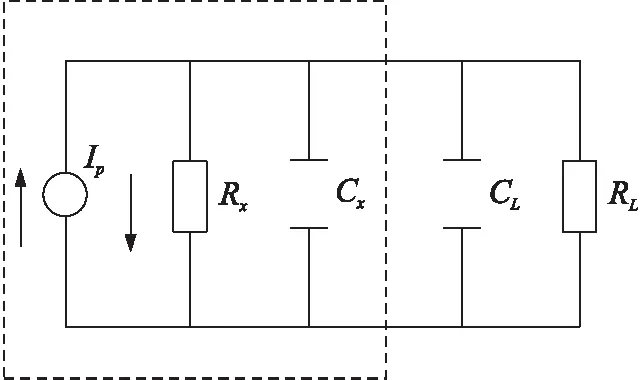
图3 传感器等效电路图

图3中,虚线框表示PVDF等效电路,Cx,RX分别为PVDF内部电容和电阻,IP表示电流源,CL和RL分别为负载电容和电阻,设定热释电信号在负载两端产生的电压U,该电路可用如下微分方程表示[12]:

(9)

式中:pc为热释电系数,S为传感器面积,dΔT/dt表示温度随时间的变化率,Req为传感器内部电阻的并联。

由此可知,传感器输出的热释电电压幅值与声源辐射声功率成正比。

图4 有限元仿真模型

2 有限元仿真分析

基于图1所示的测量原理图,利用有限元分析法建立如图4所示的仿真模型。设置聚焦换能器焦距为28.0 mm,孔径为39.0 mm且工作频率为1.27 MHz。同时将传感器放置于距离换能器28.0 mm位置。设计传感器直径15.0 mm,厚度为10.06 mm,传感器中关于PVDF和背衬材料相关参数列于表1中。

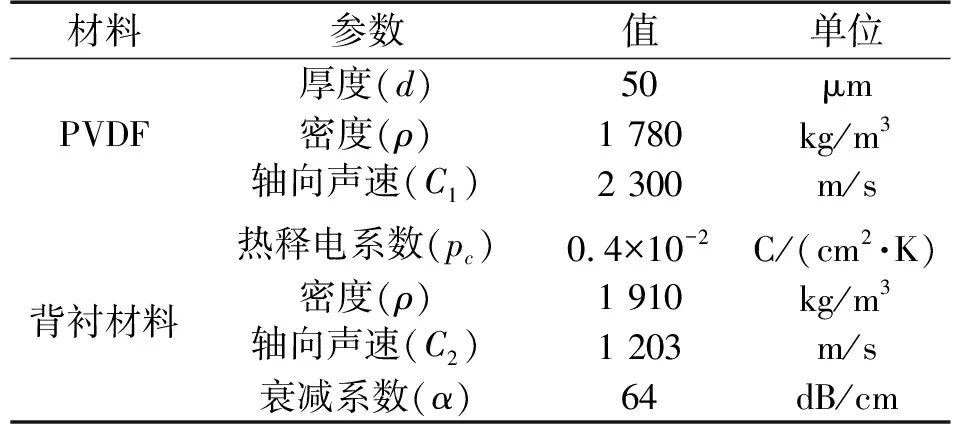
表1 PVDF和背衬材料参数

2.1 声场特性

为了进一步研究声功率测量过程中声波的传递特性,利用建立的有限元模型,选择压力声学模块进行求解,仿真结果如图5所示。超声波经水介质传播到传感器前表面,且声场焦域在传感器表面附近,由图5(a)可见,焦域内的声波波振面几乎平行,可近似看作平面波;而在背衬材料内部,由于较强的衰减作用,声波被迅速衰减吸收。图5(b)给出了沿声轴(Z轴)方向的声压分布,声压最大值出现在传感器表面附近(Z=22.0 mm～25.0 mm),声波在背衬中传播深度约为3.0 mm(Z=28.0 mm),在该点处声波完全被吸收。因此,为了准确测量超声功率,在传感器设计时,应设计背衬材料的厚度大于3.0 mm。

图5 声压分布

2.2 传感器内温升效应

传感器内部的背衬材料由于其粘滞效应将声能转化成热能,从而导致PVDF表面温升变化。为了进一步定量分析,利用有限元分析软件中热学模块,通过式(5)～式(7),求解热能在背衬材料中产生的温度变化。当超声换能器工作时间为1 s时,传感器内部温度场分布如图6(a)所示,温变区域的分布与图5(a)所示背衬材料内部的声场分布基本一致,且传感器内部最大温升值为5 K。此外,PVDF前后表面的温度曲线如图6(b)所示。随着超声辐射时间的增加,背衬材料热量的不断累积导致薄膜两表面温度迅速上升,超声作用停止后,由于热扩散的影响导致温度明显下降。且靠近背衬端的PVDF后表面温升要较前表面更大。

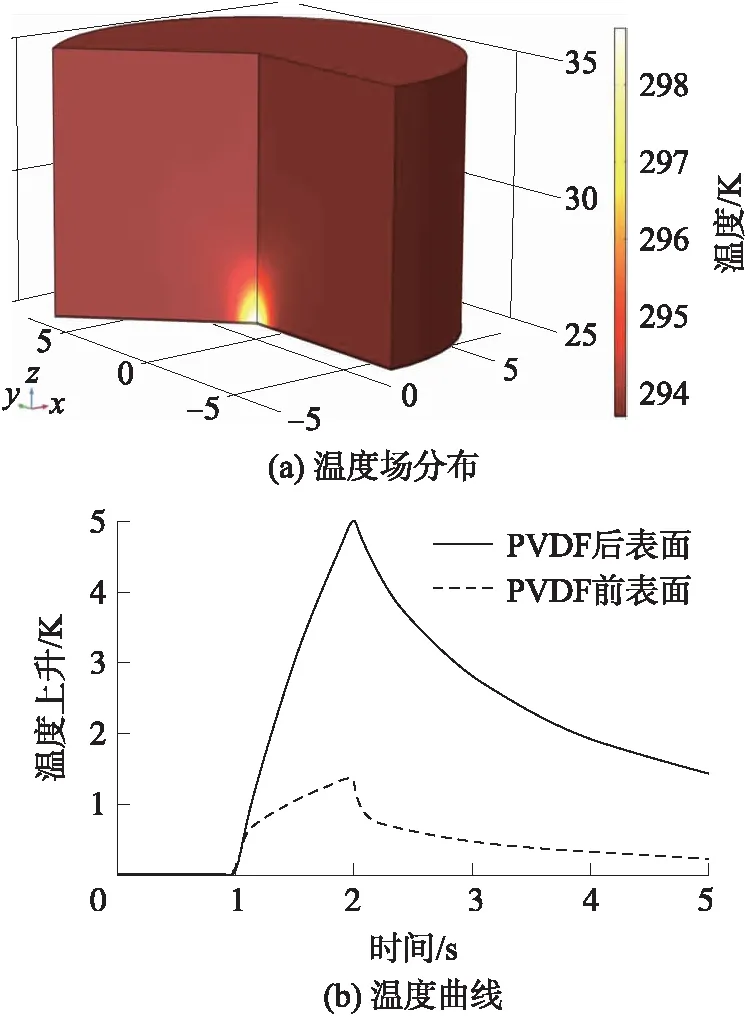
图6 传感内部温度变化

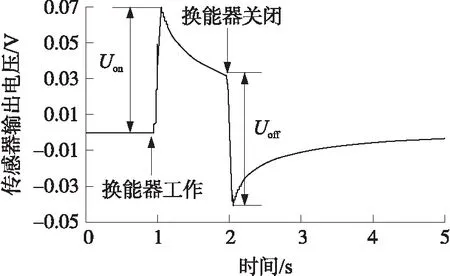
图7 热释电信号波形与幅值

2.3 热释电信号

PVDF薄膜具有热释电效应,从而在薄膜表面产生热释电电压。在上述基础上,应用式(9)对超声换能器辐射下的热释电信号进行了计算。图7表示超声作用在PVDF传感器上1 s,产生的热释电信号波形。如图所示,在开始瞬间(200 ms)热释电信号迅速上升到达峰值。这是由于换能器一旦开始工作,温度迅速上升且温度变化速率很快导致PVDF表面电荷大量积累所产生的突变。当换能器持续工作,温度上升速率变缓从而热释电信号趋于平缓,而一旦换能器停止工作,传感器将失去供能。同时,由于介质间的热交换,温度迅速下降,PVDF 薄膜表面的电荷将会反向运动从而信号出现明显的回落。最终,薄膜达到热平衡且呈电中信状态。理论上Uon(换能器工作后,传感器输出电压的最大值)与Uoff(换能器关闭后,传感器输出的电压最小值)相等,两者都可作为表征超声功率的参数。由此验证了第二部分传感器的声传感机理准确性。

3 实验与结果

为了进一步通过实验验证仿真的可靠性,以表1 所示的物理参数为选材,设计制作了如图1所示的传感器。为实现声功率测量实验搭建了如图8所示的测试系统。球型自聚焦换能器通过函数信号发生器发送电压响应至功率放大器,从而激励换能器工作。由于PVDF同时具有压电效应与热释电效应,而研究表明热释电效应发生在10 Hz以下[13]。因此在传感器输出端配备一模拟低通滤波器滤除高频压电信号从而获得低频热释电信号,最终将数据读取并储存在电脑中。

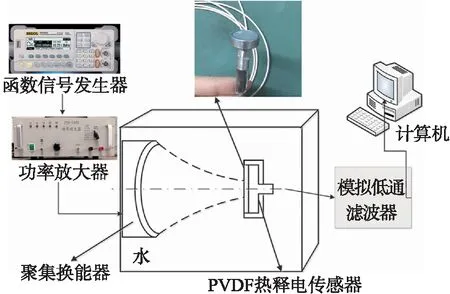
图8 测试系统

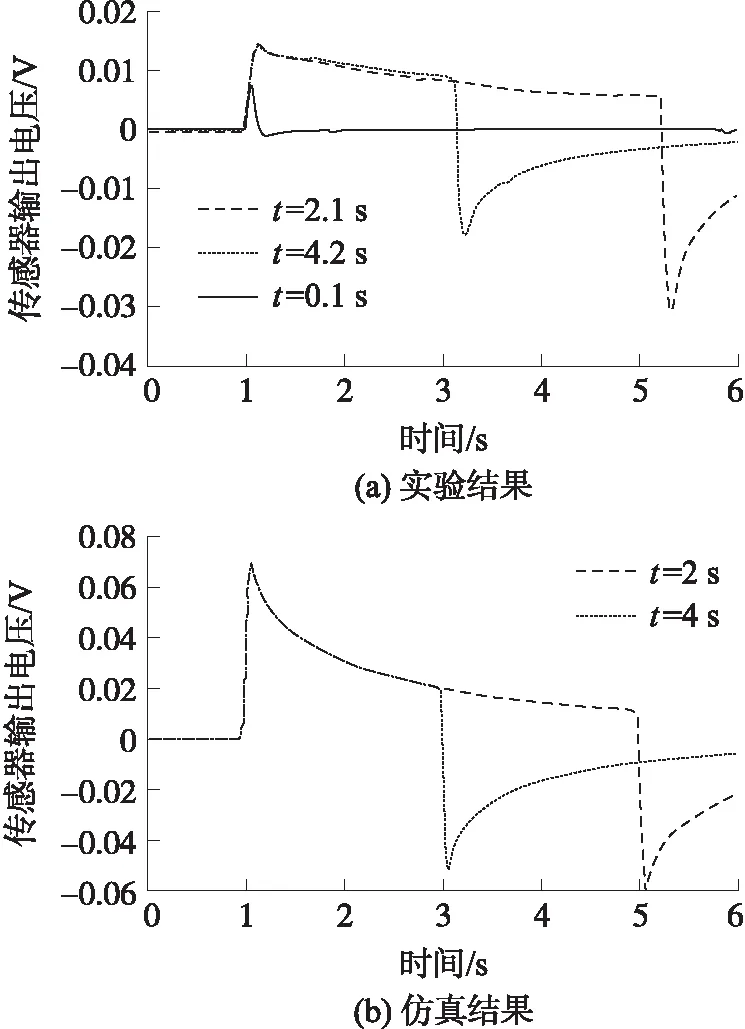
图9 传感器输出信号在不同超声辐射时间下

3.1 热释电信号的时域特性

设置聚焦换能器辐射声功率为135 mW,辐射时间分别为(t=0.1 s,2.1 s,4.2 s),则传感器的输出信号如图9(a)所示。当t=2.1 s和t=4.2 s时,热释电信号波形与仿真结果(图9(b))相似,并且时域信号的波形宽度与超声辐射时间一致,而热释电信号幅值与超声辐射时间无关。但当t=0.1 s时,热释电信号类似于脉冲波,这是由于换能器工作初期材料一直处于升温状态,热释电信号随温变速率的增大而上升但并未达到热敏响应临界点(约200 ms)。此时迅速撤去声源,PVDF表面未能达到热温平衡,从而导致信号迅速回落。

对比多次重复实验与仿真结果,信号在幅值大小上略有差异,因为在理论计算时采用绝热环境,而实际测量时由于传感器浸没在水中,导致传感器与水界面之间存在热交换。另外,由于测量过程中声波在传感器表面存在反射而导致声能量衰减。而测量值Uon与Uoff幅值存在差异,主要因为传感器与水界面之间的对流影响,以及其他混杂现象的存在。

3.2 热释电信号的幅值特性

设置换能器辐射声功率(38.7 mW,83 mW,161 mW),且辐射时间均为0.8 s,实验结果如图10所示。在相同辐射时间,不同超声功率辐射下,热释电波形不会发生改变且波形宽度均相等,而热释电信号幅值与超声辐射功率成正比,超声辐射功率越大则热释电信号幅值(Uon)越大,由此通过实验证实了该热释电传感器可用于声源辐射声功率的检测。

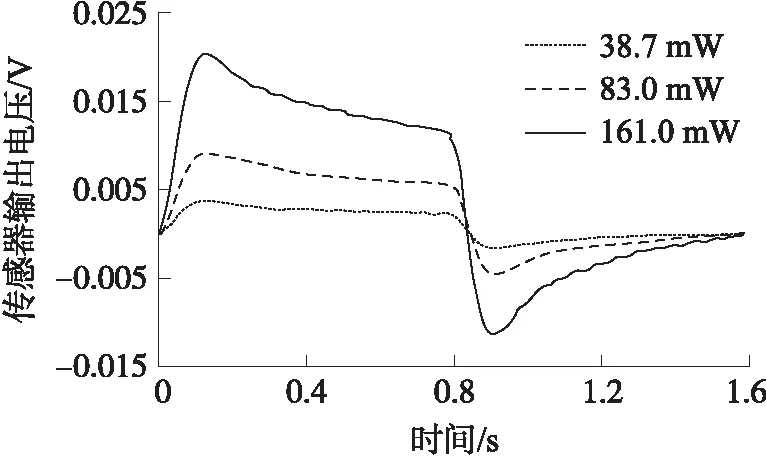
图10 不同声功率下传感器输出信号

4 结论

本文通过建立PVDF热释电传感器声功率测量的物理模型,研究了声波与热释电信号之间的转换机制。同时应用有限元分析软件计算和分析了传感器内部声场及温度分布,并预测了超声作用下热释电传感器输出信号。与此同时,制作了PVDF热释电传感器并搭建了实验测试系统。仿真结果与实验结果对比,表明该物理模型准确可靠,据分析传感器输出热释电信号与超声作用时间无关,而信号幅值与声功率成正比。

根据理论和实验研究表明,新型PVDF热释电传感器测声功率的方法被证实,且提出的物理模型可为进一步研究制造高精度声功率测量及高灵敏度传感器设计提供有利建议。而对于传感器制作工艺的提升及传感器性能评定还有待进一步研究。