基于一致性检验的航空发动机剩余寿命预测
黄 亮,刘君强,贡英杰
(南京航空航天大学民航学院,江苏 南京 211106)
0 引 言
有效地对航空发动机的剩余寿命进行预测,并在预测结果的基础上提早地制定相应的维修及备件计划,能够很大程度上减少维修费用。为降低航空发动机的维修保障费用,保证飞机的运行安全,亟需开展航空发动机剩余寿命预测的有关研究[1]。
寿命预测的研究方向主要可以分为两类:基于数据驱动的方法和基于物理失效模型。发动机的失效是由于材料在高温高压的环境下逐渐退化的结果[2]。随着各类产品变得越来越复杂化,基于物理失效模型的方法很难建立可靠的故障模型来对应产品的失效过程[3]。基于数据驱动相关的方法主要依靠产品运行过程中监测的退化数据,建立相应的退化模型,具有明显的计算和建模优势[4-5]。
目前,寿命预测的研究重点是对监测数据进行分析。文献[6]等运用数据融合的方法,实现了基于可靠性和数据驱动的在线剩余寿命预测;文献[7]则利用Kalman滤波算法融合传感器监测数据,实时地对产品退化状态进行估计。文献[8]设计和分析改进反向传播神经网络来预测发动机剩余寿命。由于Wiener过程可以用来表示退化趋势的非单调性和独立增量性,这引起了国内外学者的极大的关注[9]。目前被大量地用于对高可靠性的复杂产品进行性能退化建模[10-13]。
上述研究丰富了剩余寿命预测理论的研究,但却没有考虑到性能退化的多阶段性以及将维修前的退化监测数据用于维修后的剩余寿命预测。不同样本的信息或同一样本的不同阶段的信息是否可以融合,是基于退化模式的一致性,因此一致性问题在实际工程中是普遍存在的。当退化达到给定阈值时发生故障[14-15],产品可以通过更换一些组件来继续工作。针对现有发动机寿命预测存在的问题,提出了基于多阶段Wiener过程的正态总体均值和变异系数的一致性检测方法,根据一致性检测结果,决定是否可以融合维修前的退化监测数据,从而提高参数估计与剩余寿命预测的准确性。
1 剩余寿命预测模型
1.1 模型分析
若一个非单调的随机过程{X(t),t≥0}同时满足以下性质:X(t)为独立随机增量过程
ΔX=X(t+Δt)-X(t)~N(uΔt,σ2Δt),Δt>0
式中,X(t)是关于时间t的连续函数。那么则称该随机过程{X(t),t≥0}是Wiener过程。
基于Wiener随机过程的性能退化模型表示为
X(t)=ut+σB(t)
(1)
式中,X(t)为t时的性能退化量;u表示Wiener过程的漂移系数;σ表示扩散系数;B(t)是标准布朗运动。
由于实际航空发动机的衰退过程具有随机性和多阶段性,本文选用多阶段的Wiener随机过程构建衰退模型。多阶段的性能退化模型可以表示为
X(t)=[X(0)+X1(t)]·I(0,t1)(t)+
[X(t1)+X2(t-t1)]·I(t1,t2)(t)+…+
[X(tn-1)+Xn(t-tn-1)]·I(tn-1,∞)(t)
(2)
式中,I(t)是示性函数;ti为衰退到退化分界值的时间;X(ti)为ti时的性能退化量;Xn(t-tn-1)为第n个退化阶段的退化函数。
由式(1)和式(2)可知,航空发动机多阶段退化函数X(t)表示为
X(t)=[u1t+σ1B(t)]·I(0,t1)(t)+
[W1+u2(t-t1)+σ2B(t-t1)]·I(t1,t2)(t)+…+
[Wn-1+un(t-tn-1)+σnB(t-tn-1)]·I(tn-1,∞)(t)
(3)
式中,Wk为第k衰退阶段的分界值。
1.2 剩余寿命分布推导
剩余寿命Lt′是指从t′时的退化量X(t′)到其第一次超过失效阈值W所用的时间,Lt′表示为
Lt′=inf{X(t+t′)≥W|X(t′)≤W}=
inf{X(t+t′)-X(t′)≥W-X(t′)}
(4)
式中,Lt′表示t′时刻的剩余寿命;X(t′)和X(t+t′)分别表示在t′和t′+t时刻的性能退化量;W表示失效阈值。
随机变量Lt′的分布是逆高斯分布,其概率密度函数为
(5)
1.3 剩余寿命预测的多阶段性
令ξk表示为X(t)从初始时间到其首次超过第k个阶段分界值Wk的时间,ξk表示为
ξk=inf{t:X(t)≥Wk,t>0}
(6)
根据Wiener过程的齐次马尔可夫性质,则ξk可以改写为
ξk=ξk-1+inf{t:X′(t)≥Wk-Wk-1,t>0}
(7)
式中,X′(t)表示第k个阶段的性能退化模型。
令Δξk=ξk-ξk-1,ΔWk=Wk-Wk-1,则式(7)可以改写为
Δξk=inf{t:X′(t)≥ΔWk,t>0}
(8)
根据式(5)和式(8)可得第k个退化阶段的寿命分布的概率密度函数为
f(Δξk|uk,σk)=
(9)
由式(9)可以求得寿命T的期望表示为
(10)
当t′时的X(t′)满足X(ξk-1)≤X(t′)≤X(ξk)时,Lt′可以表示为
Lt′=(ξk-t′)+Δξk+1+…+Δξn
(11)
2 参数估计
假设共有m个同一种类型的发动机,第i(i≤m)个发动机在第k个阶段的监测时间序列为tik|1,tik|2,…,tik|n,相对应的退化监测值记为yik|1,yik|2,…,yik|n。未知参数uk,σk基于第i个发动机的第k个阶段的监测值的对数似然函数为
(12)
式中,Δtik|j=tik|j-tik|j-1;Δyik|j=yik|j-yik|j-1。
根据式(12)得m个产品的完全对数似然估计为
(13)
极大化l(uk,σk|X,m),对u,σ求偏导得
(14)
3 基于多阶段Wiener过程的正态总体均值的一致性检验
3.1 正态总体的均值区间
如果样本数据y1,y2,…,yn满足正态分布N(u,σ2),其中u,σ2都是未知的,那么称u在置信水平为1-a下的置信区间为正态总体的均值区间。
在等时间间隔下Δt=ti,j-ti,j-1,Wiener过程ΔX~N(uΔt,σ2Δt),ΔX1,ΔX2,…,ΔXn是来自第k个退化阶段的维修前的监测数据,数据的均值和方差计算公式为
(15)
(16)
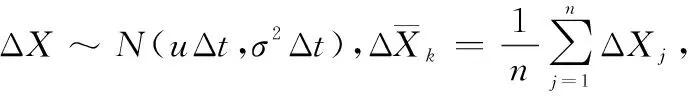
(17)
Uk是自由度为n-1的t分布,对于给定置信水平1-a下,可得
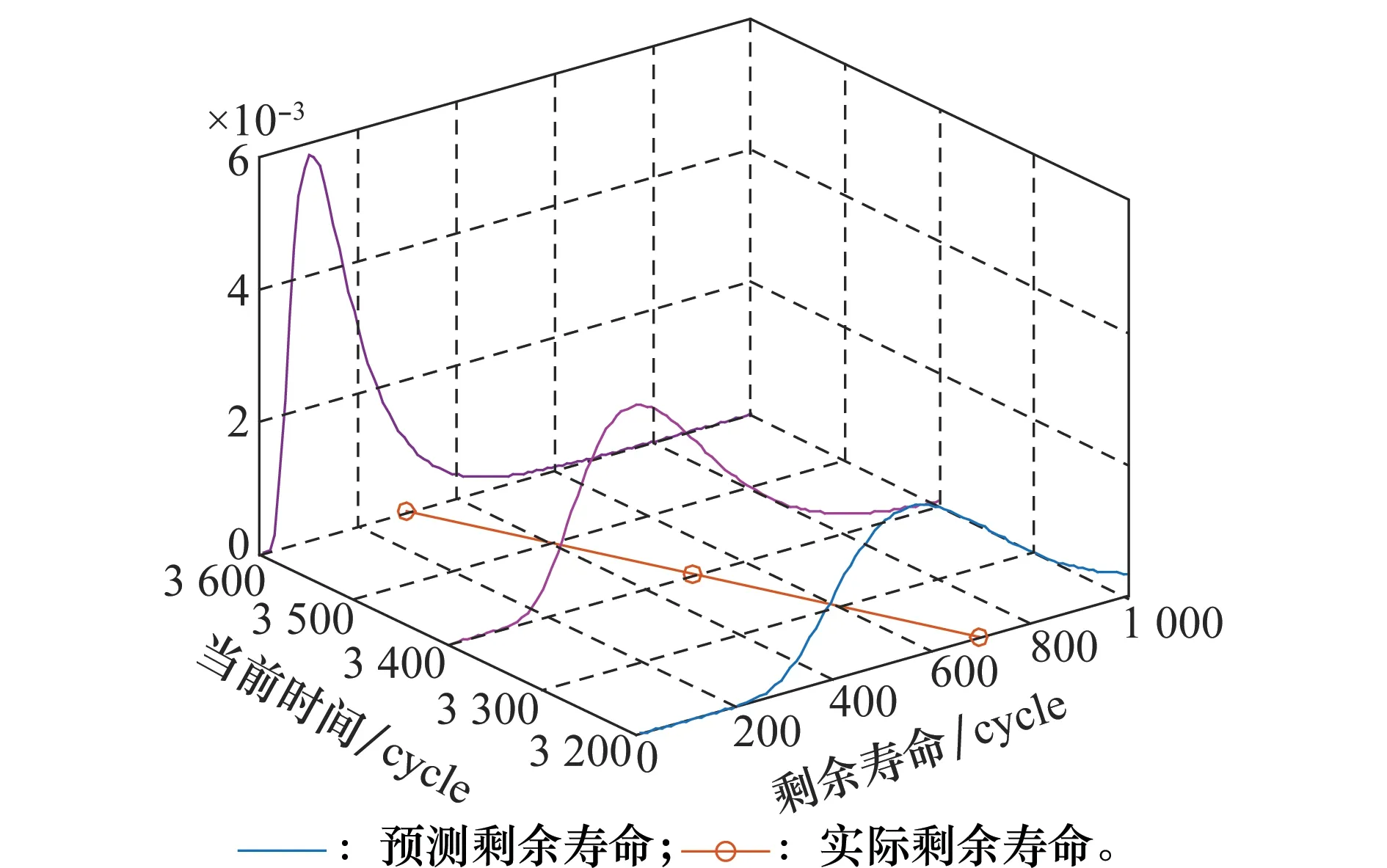
P{-ta/2(n-1) (18) 将式(17)代入式(18)中,此时可以得到 (19) 这时可获得ukΔt的以1-a为置信水平的置信区间 (20) 若对于维修后的监测数据序列y(t)的每个阶段的均值均落在维修前监测数据的正态总体均值ukΔt的置信区间内,则认为这两组监测数据的均值是一致的。该方法考虑了复杂系统性能退化的多阶段性和退化数据均值的随机性,求得每阶段置信水平为1-a的置信区间,从而在一定范围验证维修前后的发动机监测数据的均值是否具有一致性。 当维修前后的监测数据通过了正态总体均值的一致性检测之后,还需进一步检测两组数据的波动是否具有一致性。 不同样本或同一样本不同阶段的信息是否可以融合,是由退化模式的一致性决定。针对一致性验证的问题,在本文中,提出了一种基于Wiener过程变异系数的一致性测试方法。 变异系数定义为 (21) (22) 证明 (23) (24) (25) (26) 所以Hk的概率密度函数为 (27) 证毕 根据证明求得的Hk的概率密度函数,对基于多阶段Wiener过程的变异系数的一致性测试提出如下结论: (4)根据样本观测值计算hk。如果hk处于第k个阶段原假设的置信区间中,则接受原假设。否则拒绝原假设,即表明维修前后的退化数据存在显著差异。 先利用正态总体均值一致性检验方法,检验维修前后退化监测数据的各阶段正态总体均值是否一致,不一致则不融合维修前的数据,若一致则继续用基于变异系数的一致性检测方法检测维修前后各阶段的退化数据的离散程度是否一致,不一致则不融合维修前的数据,若一致则融合维修前的数据。具体步骤如图1所示。 步骤1根据式(20)对发动机维修前后的数据进行正态总体均值的一致性检测,若不通过检验则不融合维修前的退化检测数据。 步骤2若通过正态总体均值检测,则根据式(22)进行基于变异系数的的一致性检测,检测维修前后退化监测数据的离散程度。若不通过,则不融合维修前的退化检测数据。 步骤3若通过基于变异系数的的一致性检测,则融合维修前后的退化监测数据。 步骤4根据进行一致性检测后的数据,依据式(3)建立多阶段的性能退化模型,进行维修后发动机的剩余寿命预测。 图1 基于一致性检验的剩余寿命预测流程Fig.1 Prediction process of residual lifetime based on consistency test 该一致性检验算法考虑了复杂系统性能退化的多阶段性和退化数据均值的随机性,能够有效检验维修前后的数据是否具有一致性,利用变异系数的倒数构造随机变量,因变异系数的值受到数据的方差和平均值的影响,它描述了测定结果的偏差程度。 航空发动机的排气温度裕度(exhaust gas temperature margin,EGTM)是用于监测发动机运行状态的关键指标。由文献[18]的研究结果可知,航空发动机在寿命末期的退化速度加快,退化过程具有多阶段性。 表1为18台某型号发动机的性能退化数据,前12台为维修前的EGTM退化监测数据,后6台为维修后的EGTM退化监测数据。根据发动机厂商设定,EGTM的失效阈值为0℃。 表1 航空发动机的EGTM数据Table 1 EGTM data of aeroengines 图2为这18台发动机的EGTM的退化曲线,根据文献[19]中的启发式分割算法,计算性能退化分界点为27.1 ℃。因此,用两阶段的Wiener过程建立退化建模。 图2 EGTM退化过程Fig.2 Degradation process of EGTM 表估计结果Table 2 Estimated result of 表3 维修后EGTM数据的Table of EGTM data after maintenance 根据1~12号发动机的数据,利用式(14),进行性能退化量总体两阶段的u和σ2的估计,估计的结果如表4所示。 表4 维修前的u和σ2的估计值Table 4 Estimated value of u and σ2 before maintenance 表5 编号16发动机的EGTM数据的值Table 5 Values of and S2 of EGTM data for No.16 engine 表6 编号18发动机的EGTM数据的值Table 6 Values of and S2 of EGTM data for No.18 engine 编号16发动机的第一阶段的h的值为 编号16发动机的第二阶段的h的值为 编号18发动机的第一阶段的h的值为 编号18发动机的第二阶段的h的值为 根据式(27)的Hk的概率密度函数,可求得编号为16发动机的一致性检测的第一阶段置信区间为[-2.603,2.00],-2.348 8在该置信区间内,一致性检测的第二阶段的置信区间为[-4.75,2.07],-1.182 5在该置信区间内,所以编号为16的发动机的维修前后的退化监测数据的波动没有显著差异。 编号为18发动机的一致性检测的第一阶段置信区间为[-2.594,2.00],-0.673 5在该置信区间内,一致性检测的第二阶段的置信区间为[-4.75,2.07],-0.637 4在该置信区间内,所以编号为18的发动机的维修前后的退化监测数据的波动没有显著差异。 根据第6.1节和第6.2节的计算结果可知,编号为16和18的发动机的性能退化路径与维修前的12台发动机性能退化路径没有显著差异,所以可以融合维修前的退化监测数据。下面以16号发动机为例,进行融合维修前数据与不融合维修前数据的剩余寿命预测。 表7 16号发动机融合EGTM数据后的u和σ2估计值Table 7 Estimated value of u and σ2 for NO.18 engine after integrating EGTM data 融合维修前EGTM数据,利用融合后的EGTM数据对衰退模型参数进行估计,并对发动机的剩余寿命进行预测,预测结果如图3和图4所示。 图3 融合EGTM数据后的第一阶段剩余寿命概率密度分布图Fig.3 Probability density distribution of remaining life for the first stage after integrating EGTM data 图4 融合EGTM数据后的第二阶段剩余寿命概率密度分布图Fig.4 Probability density distribution of remaining life for the second stage after integrating EGTM data 为直观反映出融合了维修前的监测数据与未融合维修前的退化监测数据在航空发动机剩余寿命预测问题中的精确性,定义相对误差(relative error,RE)指标为 (28) 式中,RUL为预测的剩余寿命;T为实际的剩余寿命。 两种模型的误差计算结果如表8和图5所示。 表8 预测误差对比Table 8 Predictive error comparison 图5 预测误差对比Fig.5 Predictive error comparison 从表8可知,融合维修前退化数据的寿命预测的平均误差小于未融合维修前退化数据的寿命预测。由图5可知,随着发动机运转时间的增加,融合维修前监测数据的发动机剩余寿命预测的结果更精确。 产生以上误差对比结果的原因是当通过退化数据一致性检验后,此时的剩余寿命预测能够融合维修前的监测数据,使训练模型所用的数据量变多,排除数据的偶然性,求得的模型参数更精确,从而使剩余寿命预测的结果更加准确。 (1) 提出了基于多阶段随机Wiener过程的正态总体均值的数据一致性检验方法,用于验证维修前后退化监测数据的正态总体均值是否具有一致性。 (2) 根据变异系数的倒数构造H随机变量,并导出抽样分布,基于抽样分布提出了一种通用的一致性检验方法。该方法用于验证维修前后退化监测数据的离散程度是否具有一致性。 (3) 当维修前后的退化监测数据通过本文提出的两种一致性检验后,就可将维修前的退化监测数据用于维修后发动机的剩余寿命预测,从而提高剩余寿命预测的精度。3.2 正态总体均值一致性检验
4 基于多阶段Wiener过程的变异系数的一致性检测
4.1 构造含变异系数的随机变量



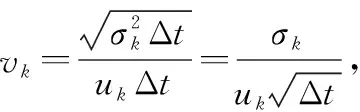





4.2 一致性测试

5 算法步骤
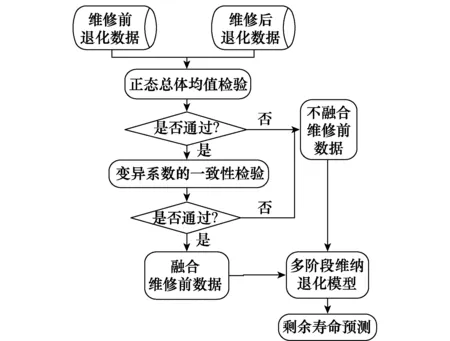
6 实例验证


6.1 基于Wiener过程的正态总体均值的一致性检验
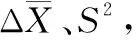


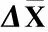

6.2 基于Wiener过程的变异系数的一致性检测

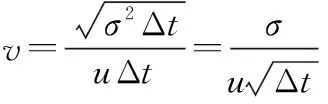



6.3 剩余寿命预测




7 结 论

