融合新型偏好度模型和改进累积前景理论的决策方法
项华春,李京峰,陈云翔,李正欣
(空军工程大学装备管理与无人机工程学院,陕西 西安 710051)
0 引 言
累积前景理论[1-5]自提出以来已被广泛应用,被认为是最有影响力的理论。该理论考虑到人们在不确定条件下的心理行为,被应用于各种决策问题,涉及资产配置[6-9]、交通管理[10-14]、多属性决策[15-19]以及应急决策[20-21]等领域。在多属性决策方面,大多数研究通常基于传统的期望效用理论,该理论假设决策者完全理性,但存在Allias悖论和Ellsberg悖论等无法解释的现象[22]。累积前景理论与期望效用理论有两个主要的偏差:非线性决策权重和损失规避。基于有限理性假设,累积前景理论解决了期望效用理论无法解决的问题,因此成为近年来研究的热点。
文献[22]针对准则值为区间直觉模糊数,准则权重分别为完全未知和部分已知的多准则决策问题,提出一种基于前景理论的决策分析方法;文献[20]针对在风险和不确定性下决策者总是有限理性的,且现有逼近理想解排序法(technique for order performance by similarity to ideal solution,TOPSIS)方法很少关注专家心理行为这一问题,提出了一种基于前景理论的区间动态参考点决策方法;文献[23]针对突发事件的动态性及信息的不确定性等特征,提出基于前景理论的应急方案动态调整方法;文献[24]针对属性权重未知、属性值为犹豫模糊集的决策问题,提出一种前景理论和逼近理想解相结合的多属性决策方法;文献[25]针对复杂环境下决策者对于应急事件做出的决策往往会面临偏好转移的问题,提出一种新的大群体风险型动态应急决策方法;文献[26]针对现实世界中发生紧急事件单个决策者很难做出全面决策且决策者理性有限的问题,引入专家心理行为,提出一种基于前景理论的群决策方法。上述研究丰富和发展了累积前景理论在决策方法上的应用,一定程度上克服了不考虑专家心理行为的局限。但是文献[22-25]所采用的心理参考点均为精确值,未能很好满足不确定性决策问题以及紧急复杂问题的实际和需求。文献[20]虽然进行了改进,将心理参考点变为区间值,但是采用单一专家决策,结果有失合理性。文献[26]在文献[20]的基础上采用专家群体进行决策改进,但专家赋权采用等权重,且属性赋权方法造成一定程度的信息丢失。
因此,针对以上不足,本文提出一种融合新型偏好度模型和改进累积前景理论的决策方法。首先考虑到决策问题的不确定性和复杂性,将属性值和心理参考点改进为区间值;然后根据区间心理参考点的二维几何表示定义新型偏好度模型,简化计算,并基于此确定专家权重和属性权重;由收益值和损失值的计算公式,确定各备选方案的前景值,结合权重向量确定总前景值,进而得到方案排序和最优方案;最后通过案例和方法对比进行验证。
1 基础理论及框架定义
1.1 基础理论
累积前景理论[1]是由Daniel Kahneman和Amos Tversky在1979年提出的前景理论[2]基础上改进得到的行为经济学理论。研究表明,人们的心理行为可以分为风险规避倾向和风险偏好倾向,同时在决策过程中,人们首先确定一个心理参考点(psychological reference point,RP),根据RP确定收益或者损失的心理预期,然后利用收益或损失的潜在价值做出决策,选择具有较高前景价值的备选方案。
根据累积前景理论中参考依赖、敏感度下降和损失规避3个重要原则,提出了S型的价值函数,定义如下。
定义1累积前景理论中以幂形式给出价值函数v(x),表示为
式中,当x≥0时,x表示收益值,当x<0时,x表示损失值;α和β分别表示对收益和损失的敏感程度,且0≤α,β≤1;λ表示风险规避参数,λ>1放大了决策者对损失的敏感程度。
1.2 群决策问题的框架定义
本文提出方法所要用到的相关符号如下所示。
E={e1,e2,…,eK}表示参与决策的专家组,其中ek代表第k个专家,k=1,2,…,K。
A={a1,a2,…,aM}表示备选方案的集合,其中am代表第m个备选方案,m=1,2,…,M。
C={c1,c2,…,cN}表示备选方案属性的集合,其中cn代表第n个备选方案属性,n=1,2,…,N。
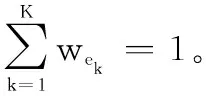
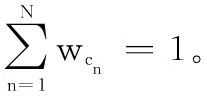
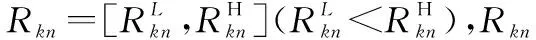
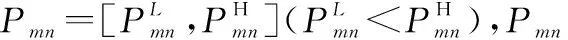
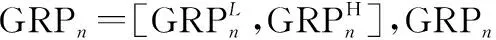
2 方法原理
2.1 新型偏好度模型
本文提出一种新型偏好度模型,该模型以几何表示(面积)为基础进行相关定义,进而设计偏好度公式,最终明确区间心理参考点之间的偏好程度。
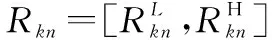
(1)
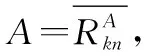
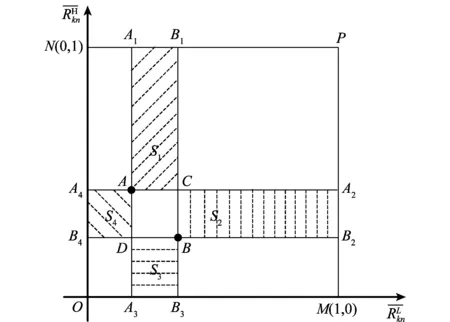
图1 规范化IRP的几何表示Fig.1 Geometric representation of the normalized IRP
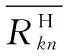
(1) 点A在线段ON上,该情景下正方形MONP被划分为两部分;
(2) 点A在线段OM上,该情景下正方形MONP被划分为两部分;
(3) 点A在线段MP上,该情景下正方形MONP被划分为两部分;
(4) 点A在线段NP上,该情景下正方形MONP被划分为两部分。
观察图1发现,四边形AA1PA2区域内所有点表示的区间心理参考点均大于点A,四边形OA3AA4区域内所有点表示的区间心理参考点均小于点A。然而,四边形NA1AA4和四边形MA2AA3区域内的点与点A之间的大小关系并不确定。

根据规范化后区间心理参考点几何表示中非重叠的四边形区域,IRP的偏好度概念定义如下。
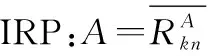
P(A>B)=
(2)
此外,需要注意一种特殊情景。当P(A>B)=0.5时,可以是xA=xB且yA=yB,亦可以是(xA-xB)(yA-yB)<0这两种条件,此时A等价于B,记作A~B。
对于xA=xB且yA=yB,A等价于B是显然的。对于(xA-xB)(yA-yB)<0这一情景,可举例说明,例如,当xA=0.2,yA=0.3;xB=0.3,yB=0.2时,P(A>B)=0.5,作图根据对称性可知,A~B。这与文献[27]中所述直觉模糊数的应用有所差别,不需要求出点A到线段MN的距离作为参考。
2.2 基于新型偏好度模型的属性权重确定
在目前多数研究中,对于不同的决策专家,属性权重被视为相同。然而在实际应用当中,因专家知识、经验及背景的差异,不同属性往往有不同的重要性。如果关于一个属性所有专家意见差异甚微,那么该属性对于决策结果影响不大。相反,如果专家意见差异明显,则该属性在决策进程中扮演重要角色。因此,对于专家意见差异明显的属性应分配较大权重,反之则分配较小权重。
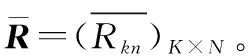
(3)
按照专家意见差异明显的属性应分配较大权重的原则,结合式(3)得到属性权重向量WC=(wc1,wc2,…,wcN),其中
(4)
2.3 基于新型偏好度模型的专家权重确定
专家权重的确定在群决策问题中至关重要,目前,已有许多不同的方法确定专家权重。文献[28]提出模糊层次分析法(fuzzy analytic hierarchy process,FAHP)确定权重,考虑过多主观因素;文献[29]利用熵值法直接求解权重,忽略专家意见;文献[30]提出一种基于距离的群决策方法,忽略了专家在决策过程中的心理行为。同时,这3种权重确定方法均是针对精确值,对本文提出的区间值不适用。
通常情况下,决策专家群体的共识程度大小反映出所有个体之间意见的一致性高低。群组意见的一致性越高,说明决策结果越合理。因此,本文认为专家ek与决策群体之间的意见分歧越小,越应该分配较大的权重,基于此,求解专家权重。
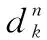
(5)
(6)
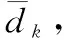
(7)
根据式(7)可以得到决策专家组权重向量WE=(we1,we2,…,weK)。
2.4 专家意见聚合
以上已经指出RP在累积前景理论中的重要性,GRP在基于改进累积前景理论的多属性群决策中同样重要。
由于单个专家形成的区间心理参考点IRP仅仅代表该专家个人意见,若以此为参考进行收益值和损失值的计算往往会造成偏差或者极端现象等情况发生,所得结果过于片面。因此,若把具有不同知识、经验背景的各个专家形成的区间心理参考点IRP,结合各个专家的权重经过加权聚合而来,得到群参考点GRP,代表所有专家的期望,便能综合考虑每位专家的意见,相比单个专家意见更加严谨、合理。其中专家权重向量已由式(7)解得,即WE=(we1,we2,…,weK)。因此,所有专家关于属性cn的区间心理参考点GRPn为
(8)
2.5 收益值和损失值的确定方法
根据累积前景理论,收益值和损失值取决于专家组的心理行为,比如风险规避或风险偏好。为了依据GRPn和Pmn对不同备选方案进行评价,有必要确定二者之间的关系。由于GRPn和Pmn均为区间值,因此有6种可能的位置关系,如表1所示[26]。
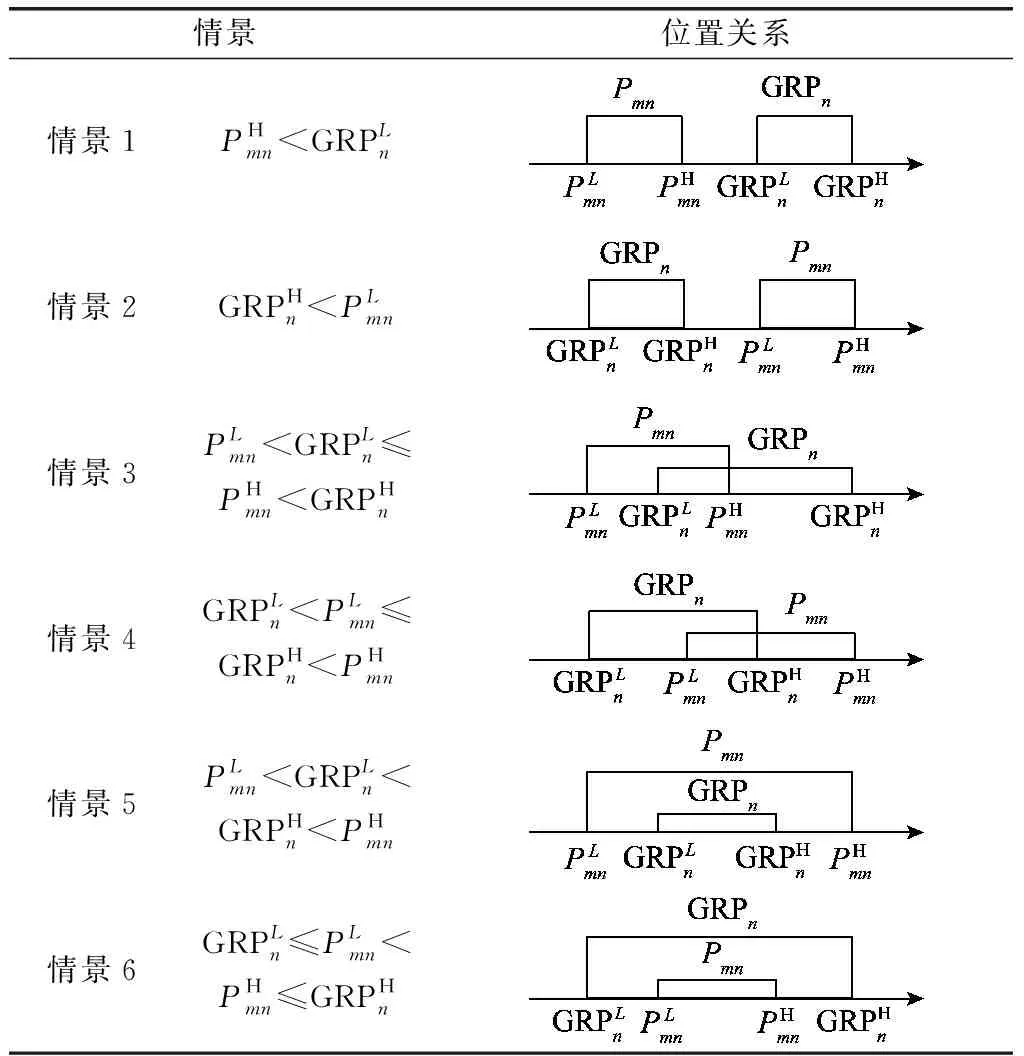
表1 GRPn与Pmn可能的位置关系Table 1 Possible positional relationship between GRPnand Pmn
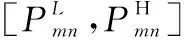
(9)
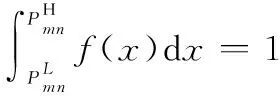
针对表1中6种不同的情景,表2和表3分别给出了对于成本型属性和效益型属性,收益值和损失值的计算公式。记备选方案am关于属性cn的收益值为Gmn,损失值为Lmn。下面仅以表2成本型属性下情景1为例解释说明。

表2 成本型属性在不同情景下的收益值和损失值Table 2 Gains and losses of cost attributes under different cases
Lmn=0,m=1,2,…,M,n=1,2,…,N
(10)
根据定义3,专家的收益为
(11)
已知变量x的概率密度函数,结合式(9)和式(11),得到
(12)

表3 效益型属性在不同情景下的收益值和损失值Table 3 Gains and losses of benefit attributes under different cases
同理,表2中其余5种情景及表3中所有公式的证明均可参考上述过程。需要特别说明的是,关于情景5,最终结果是收益还是损失取决于Gmn与Lmn之和。
2.6 前景值的确定方法
根据文献[1-2],前景值反映了专家的心理行为。当前景值大于等于0时,专家对其判断结果感到满意,否则会对其判断结果感到后悔,通过运用累积前景理论,专家的心理行为被清晰地描述。
基于表2和表3,构造“收益-损失矩阵”(GLM),令GLM=(xmn)M×N,其中xmn代表Gmn或者Lmn。由此,备选方案am关于属性cn的前景值为vmn
(13)
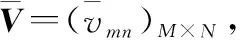
(14)
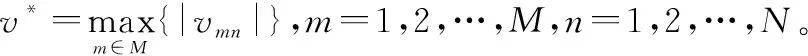
2.7 总前景值的确定方法
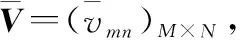
(15)
总前景值OVm越大,备选方案am越优,因此可以得到所有备选方案的排序,进而得到最优备选方案。
综上所述,本文提出的融合新型偏好度模型和改进累积前景理论的决策方法步骤如下:
步骤1问题描述,定义群决策问题的基本框架。
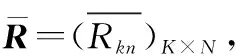
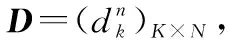
步骤4专家意见聚合。已知决策专家组权重向量WE=(we1,we2,…,weK),由式(8)得到所有专家关于属性cn的区间心理参考点GRPn。
步骤5确定收益值和损失值。根据表1判断GRPn和Pmn的位置关系,然后由表2或者表3的计算公式确定收益值Gmn与损失值Lmn。
步骤6计算前景值。利用步骤5中得到的结果构造“收益-损失矩阵”(GLM),进而由式(13)得到前景值矩阵V=(vmn)M×N,经式(14)进一步规范化处理。
步骤7计算总前景值。由式(15)得到每一个备选方案的总前景值OVm,选择最优方案。
3 案例分析
为了证明本文所提方法在解决多属性群决策问题上的适用性,利用文献[20,26]采用的研究案例(详细内容参考文献[20,26]),并与其他方法进行比较和讨论。
3.1 案例背景
案例以我国西南某地区应对堰塞湖抢险救灾为背景,在未来的72 h内,可能有4个潜在的堰塞湖紧急状态:
(1) 堰塞湖坝体不会破坏;
(2) 堰塞湖坝体1/3将破坏;
(3) 堰塞湖坝体1/2将破坏;
(4) 堰塞湖坝体全部破坏。
针对这种紧急情况,当地政府组织人员从堰塞湖上游和下游最危险的地区撤离到安全地区,并通知处于潜在危险地区的人们准备疏散。同时,提出了4种应急方案,记为A={a1,…,a4},其中包含3个属性[20],记为C={c1,c2,…,c3},c1代表影响人群,c2代表财产损失,c3代表方案成本。
a1:打开闸门的一小部分,以满足堰塞湖洪水排放的要求。
a2:打开闸门数量的一半,增加上下游堰塞湖和水电站的联合调度,减轻堰塞湖的压力。
a3:打开所有闸门,动员大型、重型机械,实施小型爆破,尽可能降低堰塞湖的水位,减小溃坝风险。
a4:打开所有水闸,增加上下游堰塞湖和水电站的联合调度。同时调动大型、重型机械,实施大型爆破,尽可能降低堰塞湖的水位,减小溃坝风险。
根据文献[26]中表7得到区间属性值矩阵P为

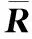

3.2 确定相关权重
(1) 属性权重
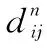
(2) 专家权重

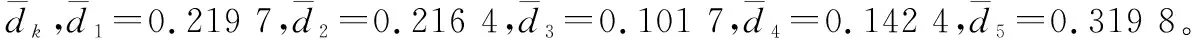
3.3 确定方案排序
通过式(8)聚合专家意见,得到所有专家关于属性cn的区间心理参考点GRPn,即GRP1=[4 521.676,7 169.228],GRP2=[3 337.25,4 396.654],GRP3=[498.524 7,561.679 5]。
由表1中GRPn和Pmn的位置关系和表2、表3的计算公式确定“收益-损失矩阵”(GLM)


通过式(15)和属性权重向量WC=(0.236 0,0.402 1,0.361 9)得到每一个备选方案的总前景值,即OV1=-0.202 3,OV2=0.088 5,OV3=0.174 3,OV4=0.132 2,备选方案排序为a3>a4>a2>a1,即方案a3为最优方案。
3.4 比较分析
为了进一步说明本文所提方法的有效性和可行性,与其他3种方法进行比较。
(1)未考虑专家在决策过程中的心理行为,使用文献[30]提出的基于距离的群体应急决策方法与本文所提方法进行比较。
(2)只考虑单个专家的意见,使用文献[20]提出的基于前景理论的区间动态参考点应急决策方法与本文所提方法进行比较。
(3)将专家权重简单视为等权重,使用文献[26]提出的基于前景理论的群体应急决策方法与本文所提方法进行比较。
3.4.1 对比方法一
由于文献[30]中方法处理的数值均为精确值,为不失公平性,分别选取矩阵P和矩阵R中区间值的下界、上界和中点计算决策结果及相关权重,如表4所示。
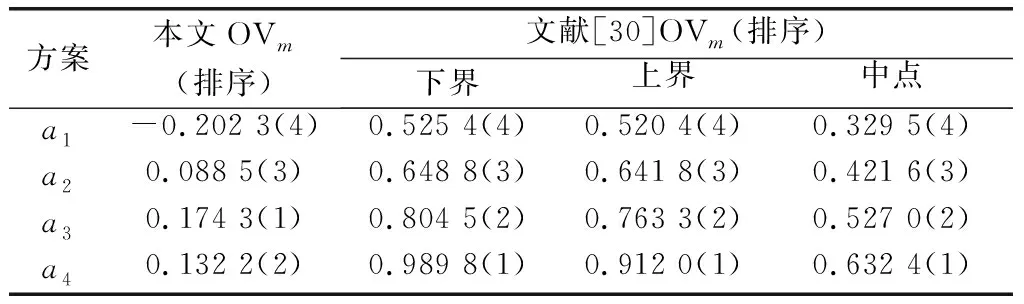
表4 方法一对比结果Table 4 Comparison results of method one
由表4可以发现,按照文献[30]中基于距离的群体应急决策方法计算出的结果与本文所得结果相似,不同点在于最优方案分别是方案a3和方案a4。这是由于本文方法中结合累积前景理论引入了决策专家的心理行为,通过考虑收益值与损失值体现专家心理行为在群决策中的重要意义,也更好地反映了现实社会中人们的思维方式及习惯,然而文献[30]没有融合这一信息。
3.4.2 对比方法二
为体现群决策的重要性,分别利用矩阵R中每个专家提供的区间心理参考点进行计算,对比结果如表5所示。

表5 方法二对比结果Table 5 Comparison results of method two
表5展示了使用文献[20]中方法,5位专家不同的决策结果。由于单一专家对情景的判断容易产生偏差,因此具有不同知识经验的专家决策结果往往不同。使用专家群体,通过分配权重聚合多人意见则会防止极端判断的产生,使决策结果更加可靠、合理。
3.4.3 对比方法三
由于文献[26]未对专家权重如何确定进行讨论,仅使用等权重显然欠缺合理性,且属性权重确定过程中只考虑各专家关于某一属性的正负参考点的距离,专家之间的相互关系没有充分体现,与本文所提方法对比结果如表6所示。

表6 方法三对比结果Table 6 Comparison results of method three
据表6可知,两种方法的排序结果相同,说明了本文的有效性与合理性,但是本文关于属性权重和专家权重的计算更加精确合理。本文属性权重向量为WC=(0.236 0,0.402 1,0.3619),文献[26]的为WC=(0.367 6,0.314 1,0.318 3),显然文献[26]的属性权重区分度不大,没有很好地突出某一属性应为关注重点,而本文的属性权重则较好地实现这一目标;本文专家权重向量为WE=(0.195 1,0.195 9,0.224 6,0.214 4,0.170 0),文献[26]为等权重,即WE=(0.2,0.2,0.2,0.2,0.2),显然将5位专家平等看待违背常识,有失合理性,本文则将5位专家加以区分,权重更加精确、合理,符合实际决策需要。
4 结 论
本文提出了一种融合新型偏好度模型和改进累积前景理论的决策方法。该方法首先以累积前景理论为基础,考虑到专家在决策过程中的心理行为,克服了以往多属性群决策方法中不考虑专家心理行为的局限。其次,将累积前景理论中的心理参考点RP进行改进,从精确值变为区间值GRP,更加符合不确定性决策问题以及紧急复杂问题的实际和需求。最后,本文提供了一种便于计算的新型偏好度模型,基于该模型确定了属性权重和专家权重,使权重更加精确、合理,进而使不同属性之间的区分度更高,专家意见更加一致。通过案例与其他3种方法公平比较,本文提供了更好的决策结果,最终证明了本文所提方法的有效性、可行性和实用性。

