基于模糊约束的军事物资配送多目标路径优化
赵文飞,孙玺菁,司守奎,刘孝磊
(海军航空大学航空基础学院,山东 烟台 264001)
0 引 言
近年来,随着信息化程度的提高、武器装备的不断发展,现代高技术局部战争呈现海、陆、空、天、电等多维态势,战争具有突发性强、节奏快、作战半径大、作战物资消耗大等特点。因此,现代战争要求军事物流系统必须做到快速反应、保障充分,并且随着战场形势的变化需要适时地调整军事物资的保障方案。而军事物资运输调度作为实现战时后勤保障精确化的关键环节,已成为现代信息化战争取胜的必要条件,所以构建合理的军事物资配送网络模型及运输路径的优化问题一直以来是各国军事物流研究的热点[1-4]。
军事物资运输问题往往是非线性多目标规划问题,属于non-deterministic polynomial (NP)问题,目前用于求解该问题的主要方法有遗传算法、蚁群算法、模拟退火等智能算法。例如文献[5]等针对现代军事物流中的车辆路径问题(fuzzy vehicle routing problem,VRP),建立了战时军事物流多目标VRP数学模型,该模型采用非支配排序遗传(non-dminated srting gnetic agorithm-Ⅱ,NSGA-Ⅱ)算法求解;文献[6]研究了车辆装备保障运输网络,提出了基于蒙特卡罗仿真和遗传算法的车辆装备运输网络化模型;文献[7]针对物流配送车辆优化调度问题,建立了多目标的优化模型,并设计了基于多目标的蚁群算法进行求解。而战时军事物资运输的各项参数往往具有模糊不确定性,从而许多学者研究了带模糊参数的VRP[8-13]。文献[8]研究了带模糊时间窗的多目标动态路径优化问题,并利用遗传算法进行求解;文献[9]考虑了一类带回路的模糊多目标车辆路径优化问题,并提出了一种启发式算法;文献[10]针对车辆旅行时间、卸货时间为模糊变量的车辆路径问题,建立了基于可信性测度的模糊机会约束规划模型;文献[11]针对战场军事物资配送中带硬时间窗VRP的模糊性,基于模糊可信性理论建立了多目标模糊期望值模型,并提出了一种改进的约束多目标粒子群优化算法;文献[12] 分析了模糊模型和模糊方法,有效地解决了车辆容量约束条件下的运输和VRP问题。但在战时军事物资运输中,随着战场态势的变换,运输路径上具有模糊性的参数较多,例如运输时间、运输费用和安全系数等参数实际上都是不确定的,具有一定的模糊性。针对这种具有特殊的多模糊约束优化问题,本文建立了模糊约束的多目标军事物资运输模型,并利用改进的多目标量子遗传算法对该模型进行求解。
1 问题的描述及数学模型
1.1 多目标优化问题
多目标优化问题[14](multiple objective problem,MOP)可以描述为这样一个极小化优化模型。
定义1MOP
Minf(x)={f1(x),f2(x),…,fm(x)}
s.t.hi(x)=0; ∀i=1,2,…,p
gj(x)≤0; ∀j=1,2,…,q
x=[x1,x2,…,xn]T∈X
式中,fi:Rn→R,∀i=1,2,…,m为目标函数;约束条件hi,gj为定义在X上的函数:Rn→R。
MOP在优化过程中,一个可行解很难使所有的目标函数达到全局最优,因此怎样定义解集是求解MOP的关键。本文采用的解集是Pareto解,其定义如下。
定义2Pareto支配
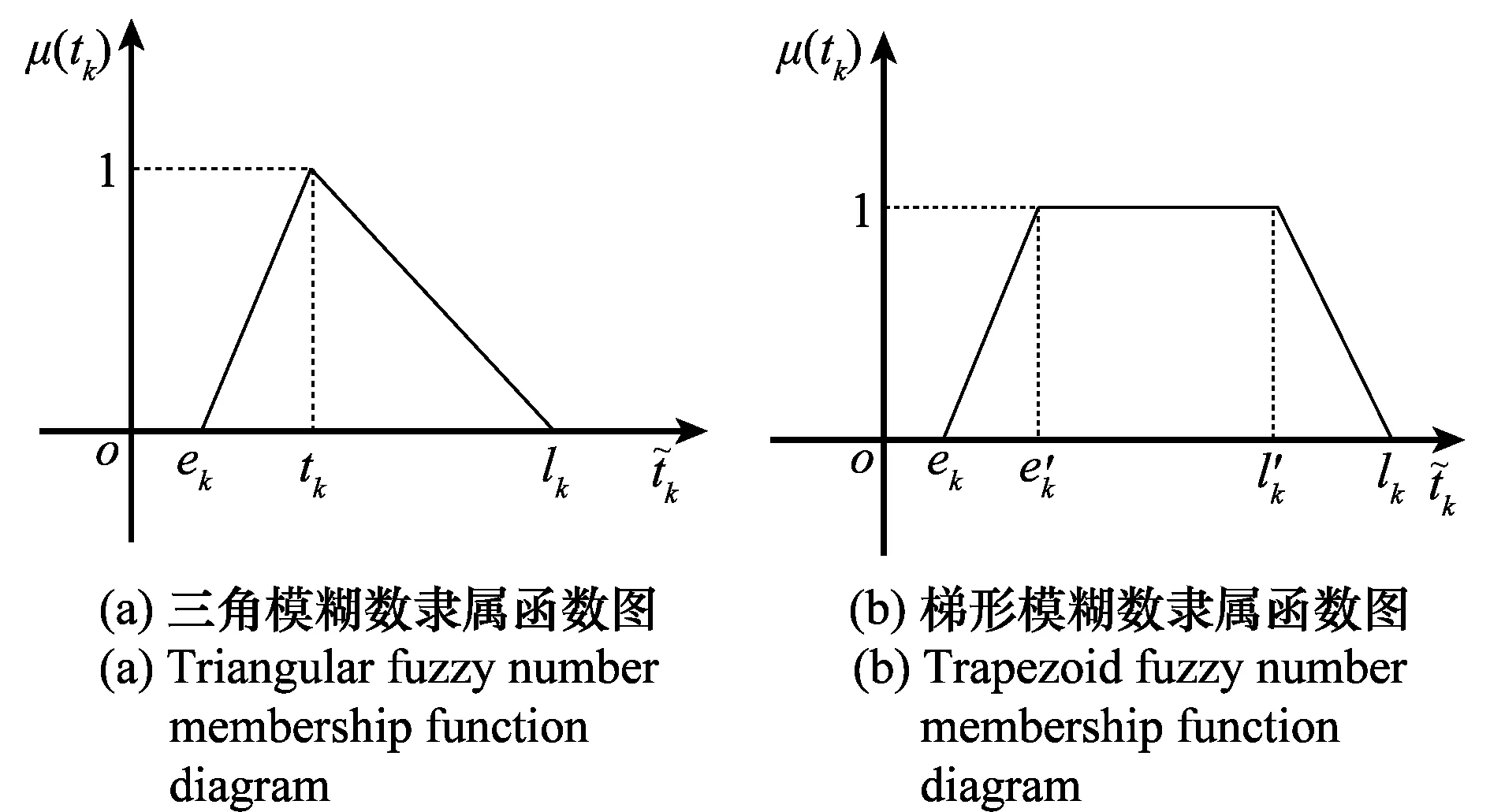
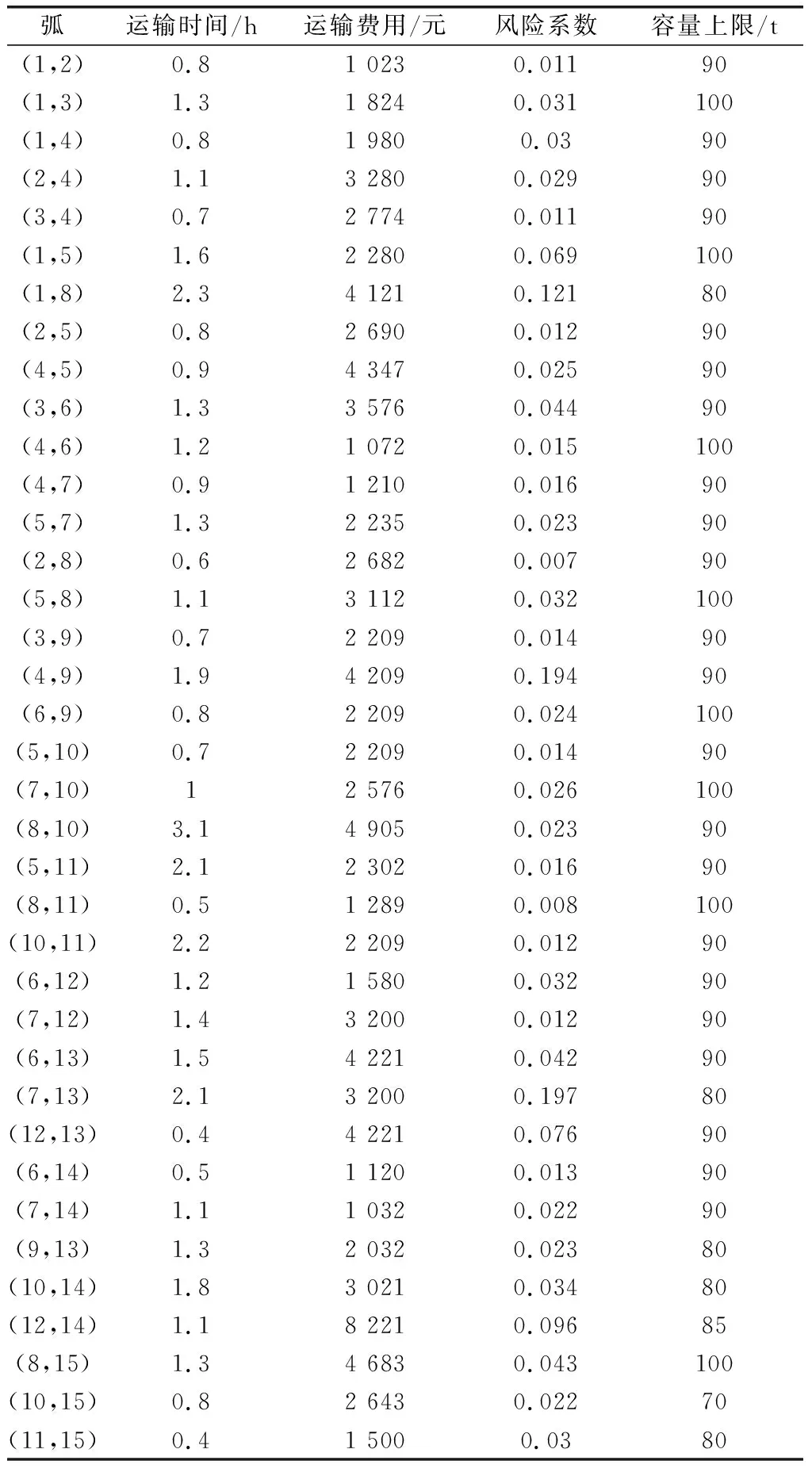
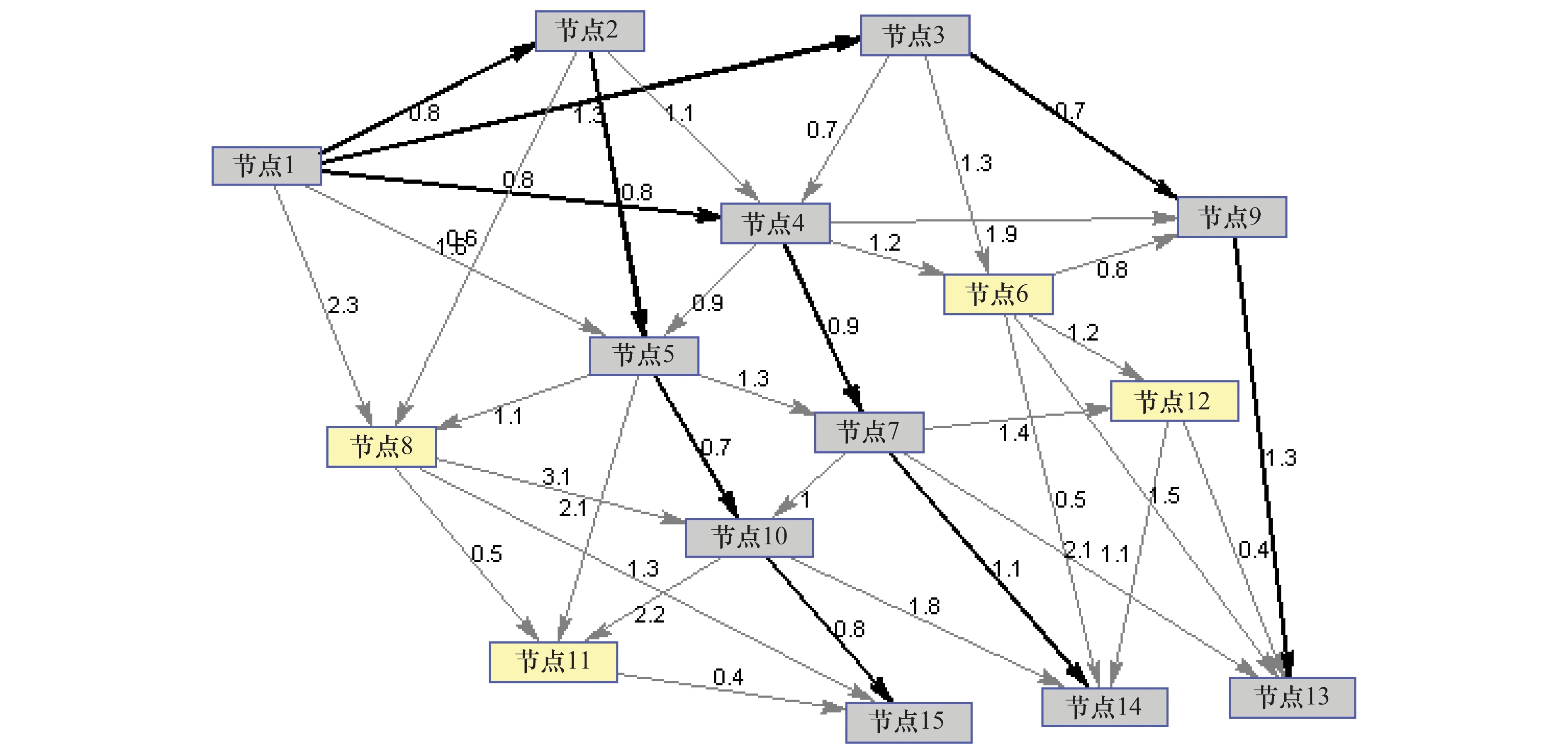
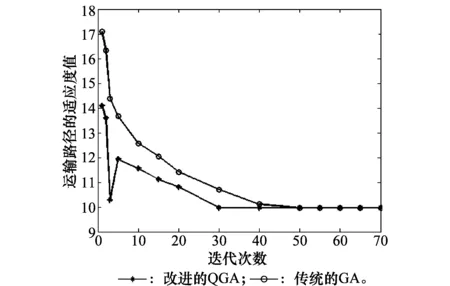
对于任意的可行解x,y,如果fi(x)≤fi(y),∀i=1,2,…,m,且∃j∈{1,2,…,m},使得fj(x) 定义3Pareto解 对于给定的MOP,可行解x为MOP的Pareto解,当且仅当不存在其他可行解y,使得ypx。 所有Pareto最优解的集合称为Pareto最优解集,Pareto最优解集的像(目标函数值)称为Pareto最优前沿。 带模糊约束的多目标军事物资配送路径优化问题可以描述为由某一军事物资配送中心v0向多个战场配送物资的VRP,在满足战场需求、运输路径的容量限制等约束情况下,求运输距离最短、费用最小、安全性能高等多个目标的优化问题。一般可以用运输网络G=(V,A,C)来表示,V表示网络节点集,表示为 V={v0,v1,v2,…,vn,s1,s2,…,sm} 式中,v0表示网络中的源点;S={s1,s2,…,sm}表示网络中的汇点;{v1,v2,…,vn}为运输路径上的节点。A={eij|eij=(vi,vj),其中vi,vj∈V}∈V×V,表示网路的弧集。C={cij|(vi,vj)∈A},cij表示弧eij上所能承受的最大容量。网络G=(V,A,C)实际上表示的是一个一对多的运输保障网络。 1.2.1 带模糊时间窗的运输时间最短的模型 由于战场上军事物资配送问题的特殊性,每个战场(汇点)sk(k=1,2,…,m)往往要求在某一个特定的时间窗[ek,lk]被服务,否则将延误战机。这里我们将每一个战场被服务时间窗口视为一个模糊数,模糊数是定义在实数域上的正规凸模糊集,最常用的模糊数为三角模糊数和梯形模糊数,这两种形式都是根据其隶属函数的几何形状命名的,如图1所示。 图1 三角模糊数和梯形模糊数隶属函数图Fig.1 Triangular fuzzy number and trapezoid fuzzy number membership function diagram 式中,目标函数越大,说明整个战场军事物资保障越及时,约束条件反映了每个战场必须在固定的时间窗口内接收到物资。 事实上,还可以根据战时每一个战场的战略地位不同,对每一个战场分配一个权值λk,这样优化模型更改为 1.2.2 带模糊约束的运输费用最小模型 在经典的运输问题中费用最小的优化模型为 但这只适用于静态的运输网络,战时由于网络路径随时都有可能遭到敌方不同程度的破坏,在运输过程中受多种不确定因素的影响,而仅用一个确定的数额来刻画每一条弧上的单位运输费用不符合实际。为此,这里将单位运输费用wij视为一个三角模糊数。基于该假设可得运输物资费用最小模型为 1.2.3 带模糊约束的风险最小模型 在运输网络中,弧eij受攻击的概率(不安全系数)为qij(0≤qij≤1),则路径P的风险值为 因此风险最小的目标函数为 1.2.4 模型建立 基于以上假设和分析,建立带模糊约束的多目标军事物资运输路径优化模型为 (1) (2) (3) (5) (6) (7) 0≤fij≤cij,∀(vi,vj)∈A (8) (9) (10) (11) 其中,式(1)~式(3)是目标函数;式(4)为运输过程中可行路径的约束条件;式(5)为可行流的约束条件;式(6)为时间约束,要求可行路径总的运输时间必须在指定的时间区间[ek,lk]; 式(7)和式(8)表示流量需满足战场的物资需求和运输道路的容量限制; 式(9)~式(11)为模糊数和参数的设置要求。 求解第1.2.3节建立的带模糊约束的多目标军事物资运输路径优化模型,重点是怎么将带模糊约束的模型转化为确定性模型。文献[15-16]分别利用模糊运算和效用函数将模糊约束转化为清晰的等价类来进行处理;文献[17]利用隶属函数,给出了三角模糊数取值区间的期望值和取值的期望值。本文受Jiménez的启发,将带模糊约束的模型转化为确定性模型来求解。 从而运输费用最小模型可调整为 同理,风险最小模型可修改为 综上所述,带模糊约束的多目标军事物资配送问题可转化为 (12) (13) (14) 其中约束条件依然为式(4)~式(11)。 通过第1节的处理,本文将带模糊约束的多目标物资运输问题转化为一个带不等式的确定性约束的多目标规划问题。针对这个优化问题,将对传统的量子遗传算法(quantum genetic algorithm,QGA)进行改进来求解。事实上,目前很多学者利用QGA 来求解物资运输路径优化问题[18-19]。QGA利用量子计算中的量子比特和量子态叠加等概念和理论[20],将染色体的编码用量子比特的概率幅来表示,使得一个量子比特染色体可以同时表示多个状态,能以较小的种群表示较多的可行解。然后依据当前最优染色体的个体信息,利用量子旋转门对染色体进行有效的更新,而不是采用传统的交叉和变异的操作。本文对传统的QGA算法进行改进,在算法中引入非支配排序和小生境密度,对种群中的个体进行前沿非劣分级,并采用精英保留策略,使得较优的个体能够保存下来,这样能够有效地提高算法的寻优效率。 在经典计算中,采用0和1二进制表示信息,通常称其为比特。在量子计算中,采用|0〉和|1〉表示微观粒子的两种基本状态,称其为量子比特。经典比特与量子比特之间的区别在于,量子比特的状态除了|0〉和|1〉,还可以是其线性组合,通常称为叠加态,即 |φ〉=α|0〉+β|1〉 式中,α和β是一对复常数,称为量子态的概率幅,满足|α|2+|β|2=1。 一个量子比特可同时包含0和1的信息,则m个量子比特可以表示2m个不同的状态。含m个量子比特的个体j可表示为 式中,|αi|2+|βi|2=1;∀i=1,2,…,m。 式中,L为染色体的基因位数;n为每个基因的量子比特数。 实际上在解码中是将量子的不确定性转化为一个确定个体的过程,其表示方式为二进制编码,需进一步将其转化成十进制数,这样染色体的每个基因就对应成一个自然数,而每个自然数就对应于网络中的一个节点。例如|011〉转化为十进制数就是3,它代表网络中节点3。染色体的每个基因都这样处理后,整个染色体就表示成自然数编码,其中自然数的顺序就是运输网络路径中节点的顺序。 在解码的过程中,有可能会出现非法解的情况,主要有两种:编码的重复和越界。因此,在解码的过程中需要适当的修正,对于重复的编码,直接去掉,例如染色体对应的路径P=[012325],重复路径为232,直接去掉修正后为P=[0125];对于越界的编码,则在依概率选取量子态时去掉越界的量子态即可。如果经过修正后得到的解不满足约束条件则直接去掉。 通过第2.2节得到的每一个可行解都有3个评价指标:战场的满意度、运输费用和安全性,为此本文采用非支配排序和小生境密度来评判解的优劣程度。 对于每一个可行解X都设有两个参数Xrank和Xid,其中Xrank为非支配排序,将解分为0,1,…,n个等级,同一个等级非支配序相等,取值越低的解越优秀,例如Xrank 式中,V(X)表示个体X中的所有节点的集合;A(X)为个体X中的所有弧的集合;||表示集合的势。不难看出,Xid越高的解,反映在运输路径上表示该路径与同等解集F中其他路径相似程度较高,即该运输路径上比较拥挤,反之则比较稀疏。 旋转门的更新是量子进化算法的关键。本文设计的量子旋转门为 从而旋转角度为 (15) 种群中的个体可以根据适应度函数值的优劣来进行排序,为了使每一代优秀的个体能够继续保留下来,在迭代时将父代中较为优秀的个体保留下来直接进入子代。具体操作为: 在第t代父代种群Q(t)中,计算每个个体的适应度函数并进行优劣排序,然后根据种群规模确定一定数量的优秀个体用集合Γ(t)表示,再在Q(t)中随机选取个体进行量子变异产生子代种群P(t),其中量子变异以量子旋转门更新的方式进行。最后通过计算集合Z(t)=P(t)∪Γ(t)中个体的适应度函数进行排序,选取满足种群个数的最优个体作为第t+1代父代种群Q(t+1)。 通过前面的讨论和分析,设计本文算法的主要流程如下: 步骤2按照第2.3节的方法,计算种群Q(t)中每个个体的适应度函数并进行排序,选取适应度函数较优的个体记为Γ(t)。 步骤3对种群Q(t)中的每个个体按照第2.4节的方式进行量子变异得到种群P(t)。 步骤4令Z(t)=Γ(t)∪P(t);计算Z(t)中每个个体的适应度函数并排序,选取前N个个体作为新一代种群Q(t+1)。 步骤5若t 因本文所研究问题背景的特殊性,目前没有统一的测试案例,为此选取文献[22]中案例的运输网络来进行仿真实验分析。将案例中运输网络的节点1设为源点,即配送中心,网络中节点13,14,15设为汇点,即模拟为战时的3个战场。由于本文研究的是带模糊约束的多目标路径优化问题,因此在仿真时,需对运输网络中给定的参数进行修正,将运输时间参数ti调整为三角模糊数(tij-0.1 rand,tij,tij+0.1 rand);运输费用参数wij改为三角模糊数(wij-10 rand,wij,wij+10 rand);风险系数qij改为(qij-0.01 rand,qij,qij+0.01 rand)。然后采用第1.3节的处理方法,处理之后的数据如表1所示。3个汇点的模糊时间窗口参数如表2所示。 表1 军事物资配送网络G中各项权值参数Table 1 Weight parameters G of military material distribution network 表2 模糊时间窗口参数明细Table 2 Parameters of fuzzy time window 根据前面建立的数学模型和设计的算法,将运输时间、运输费用和安全性作为单目标进行优化,分别寻找5条较优的路径作为初始种群,利用改进的QGA算法,用Matlab软件编程仿真,迭代100次,得到节点1到节点13,14,15运输最优的路径如图2所示。 图2 最优运输路径Fig.2 Optimal transportation route 从图2中可以看出节点1到节点13,14,15的最优运输路径分别为1→3→9→13,1→4→7→14和1→2→5→10→15,其中各运输路径的相关参数如表3所示。事实上因为每一个汇点都带有模糊时间窗口的限制,所以运输路径的各项参数不一定是最优的。若不考虑模糊时间窗口的约束条件,只考虑运输时间少、费用低和风险系数低的优化问题,则最优的运输路径方案及相关参数如表4所示。 表3 带模糊时间窗口的最优运输路径及相关参数Table 3 Optimal transportation path and related parameters with fuzzy time windows 表4 不带模糊时间窗口的最优运输路径及相关参数Table 4 Optimal transportation path and related parameters without fuzzy time windows 对比表3和表4不难发现,若不考虑汇点带模糊时间窗口的约束条件,节点13的最优运输路径方案不受影响,而表4中节点14和节点15的最优运输路径为1→4→6→14和1→2→8→11→15,其实验参数明显比表3中节点14和节点15的最优运输路径1→4→7→14和1→2→5→10→15要好,但是正因为运输时间少导致不满足节点14和15的时间窗口约束,从而在算法中把这样的路径排除。 此外,将本文提出的改进的QGA与传统的GA进行对比,虽然都能够得到最优的运输路径,但本文提出算法的收敛性效果较好,如图3所示。 图3 适应度值比较Fig.3 Fitness comparison 本文针对战场上带模糊时间窗口、模糊运输费用以及模糊运输风险问题,建立了带模糊约束问题的多目标运输路径优化模型,并利用改进的QGA对其进行求解。虽然多目标运输路径优化问题很难找到绝对最优的运输方案,但仿真结果表明,将改进QGA算法用于求解该问题,决策者能够有效地获得最优的运输方案以及最优的备用运输路径,根据仿真结果中的各项参数值自行择优选择运输方案。本文提出的建模方法和算法能够有效的解决带模糊约束的运输路径优化问题。1.2 带模糊约束的多目标军事物资配送问题
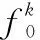
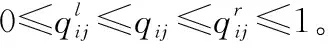
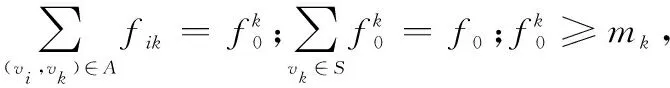

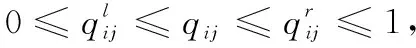
1.3 模型求解
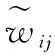
2 算法设计
2.1 量子位
2.2 量子比特编码与解码

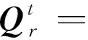
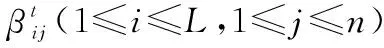
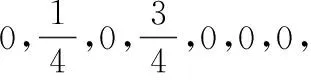
2.3 确定适应度函数
2.4 旋转门的更新
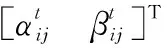

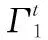
2.5 精英保留策略
2.6 算法流程

3 实例分析



4 结束语

