基于幅度信息的标签多伯努利滤波算法

彭华甫,黄高明,田 威,3,邱 昊

(1.海军工程大学电子工程学院,湖北 武汉 430033; 2.中国人民解放军92773部队,

浙江 温州 325807; 3.中国人民解放军91715部队,广东 广州 510450)

0 引 言

多目标跟踪(multi-target tracking,MTT)的目的是在目标个数时变且未知的条件下,利用传感器获取的量测数据估计所有目标的状态[1-2]。实际应用中,由于传感器本身的特性,目标检测存在虚警、漏检现象,导致量测数据中包含杂波、部分真实目标由于漏检未能获取量测[3-4]。跟踪器需要从杂波污染的量测数据中识别出真实目标量测,利用目标运动模型完成目标跟踪。

由于地杂波、海杂波、大气杂波以及人为电子干扰等因素的影响,实际量测数据不可避免会引入杂波,从而降低目标跟踪效果[5]。在声纳、雷达等应用中,目标量测包括:距离、方位角、多普勒、幅度等信息。通常真实目标回波幅度大于杂波幅度,因此,可利用幅度信息区分目标量测与杂波量测,抑制杂波影响。

针对多目标跟踪问题,传统解决方案是一种自下而上的方法,其将多目标跟踪过程分解为数据关联和状态估计两部分。文献[6]将目标幅度信息引入到概率数据关联(probabilistic data association,PDA)滤波器中,改进了跟踪滤波的性能;随后文献[7-8]分别将幅度信息引入到多假设跟踪(multiple hypothesis tracking,MHT)框架以及Viterbi数据关联框架下,改进了数据关联效果。

然而传统多目标跟踪算法存在“组合爆炸”所导致的计算瓶颈。基于随机有限集(random finite set,RFS)理论[9]的多目标跟踪方法,能够将单目标贝叶斯滤波框架直接扩展至多目标情形,避免了传统方法复杂的数据关联过程,成为目前多目标跟踪领域的研究热点[10-11]。为简化计算,先后提出了概率假设密度(probability hypothesis density,PHD)、势概率假设密度(cardinalized probability hypothesis density,CPHD)滤波器、多目标多伯努利(multi-target multi-Bernoulli,MeMBer)滤波器。为提高杂波环境适应能力,文献[12-13]引入幅度信息,提出了幅度信息概率假设密度(amplitude information-PHD,AI-PHD)滤波算法,以增加少量计算复杂度为代价,有效改进了仅基于方位量测的跟踪算法。由于PHD及CPHD均为多目标后验概率密度函数的矩近似,其目标跟踪精度有限,且序贯蒙特卡罗(sequential Monte-Carlo,SMC)实现时状态提取需要复杂的聚类过程。MeMBer滤波器基于数值近似,具有更高的精度,且状态提取简单。文献[14]通过引入幅度信息,提出了基于随机有限集的幅度信息辅助多伯努利滤波(amplitude information assistant multi-bernoulli filter,AIA-MBerF)算法,提高了目标跟踪精度。这些算法虽然在杂波环境下性能有一定的改善,但囿于PHD及MeMBer滤波器本身的缺陷,仍需要较高的信噪比,且无法直接估计航迹。

近年来,B Ngu Vo等提出了一种广义标签多伯努利(generalized labeled multi-Bernoulli,GLMB)滤波器[15-16]。同PHD、CPHD、MeMBer滤波器相比,GLMB无需共轭近似处理,具有更高的精度,抗干扰性能良好且可直接估计目标航迹。为降低计算量,文献[17]基于量测分组并行处理,提出了LMB滤波算法;文献[18-20]结合吉布斯采样裁剪以及预测更新合并,提出了一种GLMB快速实现算法;文献[21]基于矩近似,提出了τ-LPHD/LCPHD滤波器。为扩展算法的应用范围,文献[22-23]通过引入多模型(multi model,MM),提出了多模型标签多伯努利(multi-model labeled multi-Bernoulli,MM-LMB)滤波算法,提高了对多机动目标跟踪的适用性;文献[24-26]将其应用于多传感器多目标跟踪领域。

本文通过结合幅度信息的杂波抑制能力及GLMB的抗干扰特性,提出了一种基于幅度信息的GLMB滤波(amplitude information-GLMB,AI-GLMB)算法,进一步提高杂波环境下的适应能力,并可直接估计目标航迹,具有更高的跟踪精度。

1 GLMB滤波器及目标模型

1.1 GLMB滤波器

假设Xk和Zk分别为k时刻多目标状态集合和量测集合,Z0:k=Z0,Z1,…,Zk为观测集合序列,πk-1(·|Z0:k-1)、πk|k-1(·|Z0:k-1)和πk(·|Z0:k)分别为多目标先验分布、预测分布及后验分布。则多目标贝叶斯预测和更新方程分别为

πk|k-1(Xk|Z0:k-1)=

(1)

(2)

式中,fk|k-1(·|·)为多目标状态转移函数;gk(·|·)为多目标观测函数。

GLMB通过引入标签信息扩展目标属性,标签RFS状态可表示为

X={(x,l)i}i=1,2,…,N

(3)

式中,x为单个目标状态向量;l为其对应的标签;X∈Xs×L,Xs为目标状态空间,Ls为离散标签空间。则GLMB分布可描述为

(4)

Δ(X)=δ|X|(|L(X)|)

(5)

(6)

式中,C为离散的索引空间;wc(·)为权值函数;pc(·)为单目标状态分布;L为X×L→L的映射函数,即L((x,l))=l,L(X)={L(x):x∈X}为X的标签值集合;|·|为取势计算。

为便于处理,可将GLMB分布简化为δ扩展GLMB(δ-GLMB)分布为

(7)

式中,I∈F(L)为标签集合,F(L)表示L中所有有限子集空间;ε∈Θ为关联索引,Θ为关联空间;每对(I,ε)表示一种关联假设,ω(I;ε)为相应权值;p(x,l;ε)为单目标概率分布。

1.2 目标模型

1.2.1 扩展幅度信息的目标模型

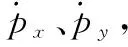
为引入幅度信息,分别对目标状态及量测模型进行扩展,得到相应的扩展形式

(8)

(9)

式中,1+S为回波信号信噪比(signal-to-noise ratio,SNR);a为回波信号幅度,且有

SNR(dB)=10lg(1+S)

(10)

1.2.2 幅度模型

雷达系统中,目标回波信号的SNR往往是随机变化的,依据文献[6]将回波信号幅度建模为瑞利分布,则目标幅度及杂波幅度的概率密度分别表示为

(11)

(12)

假设检测门限为τ,则经过门限检测后,目标及杂波幅度的概率密度可表示为

(13)

(14)

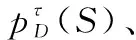
(15)

(16)

2 基于幅度信息的GLMB滤波器

由于目标的幅度信息仅与回波SNR有关,实际中SNR估计困难,可进行简化处理,即

(17)

2.1 基于幅度信息的似然函数建模

(18)

(19)

式中,ga(a|S)、ca(a)分别为检波后目标幅度似然函数及杂波幅度似然函数,有

(20)

(21)

(22)

(23)

实际中,在监视区域内,各目标回波信号的SNR各不同且非固定。假设SNR在dB域[dB1,dB2]范围内为均匀分布,其对应参数S的取值范围为[S1,S2],则目标幅度似然函数可简化表示[6]为

(24)

2.2 AI-GLMB滤波器

假设k-1时刻,多目标后验密度为

πk-1(X)=Δ(X)·

(25)

新生目标概率密度可表示为

(26)

式中

(27)

式中

ωk|k-1(I;ε)=ωP,k(I∩Lk-1;ε)ωB,k(I∩Bk)

ρε,k(l)=<1-pS,k(·,l),pk-1(·,l;ε)>

pk|k-1(x,l;ε)=

1Bk(l)pB,k(x,l)

式中,pS,k(·)为目标存活概率;Lk|k-1=Lk-1∪Bk;1I(·)为定义于集合空间的指示函数

(28)

式中

式中,Lk=Lk|k-1;pD,k(·)为目标探测概率;对于k时刻每组预测假设(I,ε),ζk代表目标到量测的关联映射{l1,l2,…,l|I|}→{0,1,…,|Zk|},当ζk(l)>0时,目标与空量测关联,即该目标漏检;当ζ(l)>0时关联具有唯一性,即ζk(l)=ζk(l′)>0时l=l′。

2.3 AI-GLMB滤波器SMC实现

假设k-1时刻多目标后验分布粒子描述为

(29)

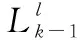
(30)

其中

更新过程中,粒子状态保持不变。k时刻后验分布粒子集为

(31)

其中

3 仿真实验

3.1 参数设置

考虑二维非线性运动场景,目标状态转移矩阵及过程噪声协方差矩阵分别为

式中,σv=0.1 m/s为噪声标准差;Ts=1 s为传感器扫描间隔。

传感器量测包含直角坐标位置和幅度,量测范围为[-1 000,1 000]×[-1 000,1 000],观测矩阵及观测噪声协方差矩阵分别为

式中,σw=5 m为量测噪声标准差。

3.2 仿真实验分析

目标新生、消亡、漏检、虚警等均依相应的概率发生,观测场景中最多同时有8个目标,单次实验目标真实航迹及量测如图1所示。

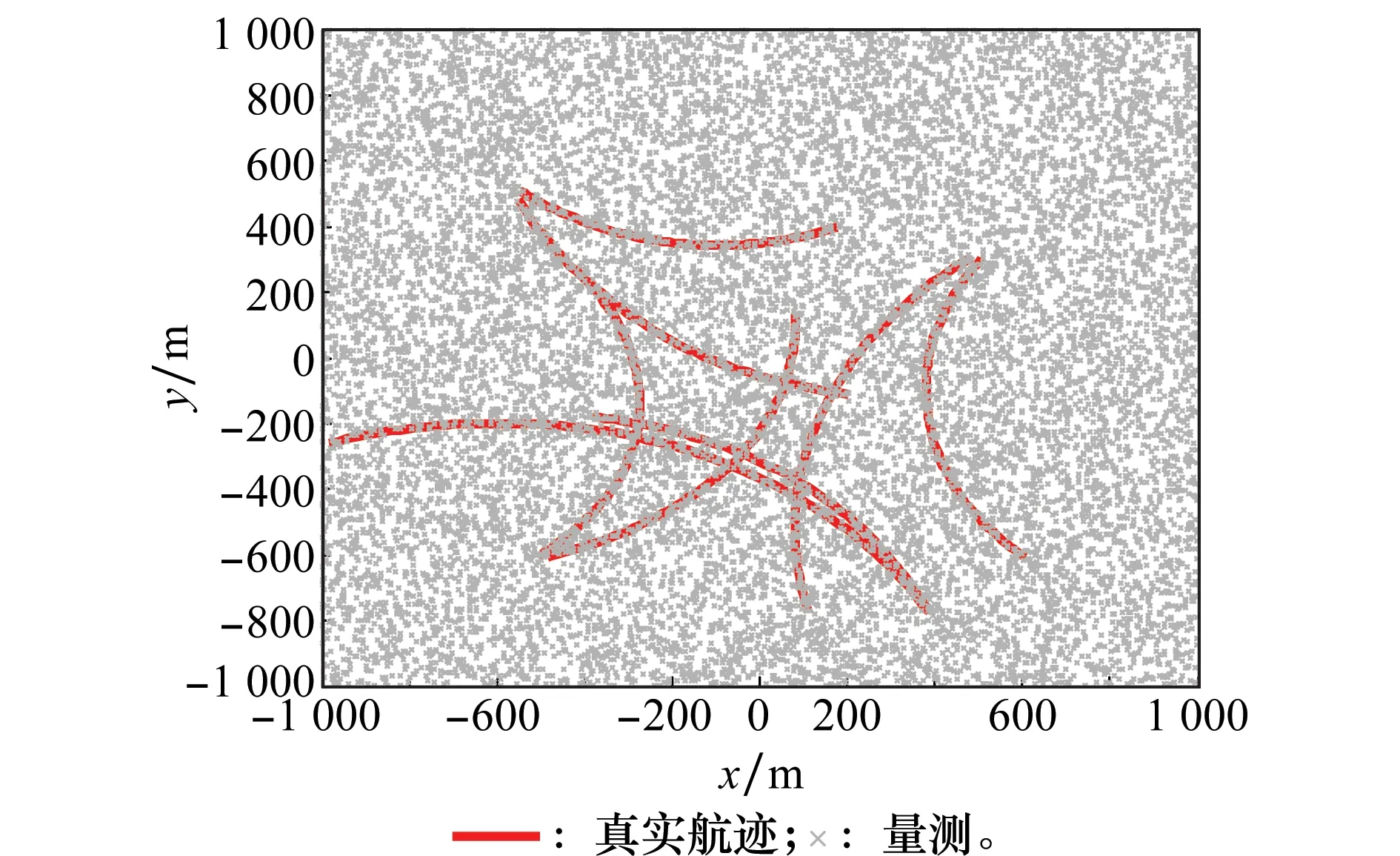
图1 单次实验目标真实航迹与量测Fig.1 True trafectories and measurements of a sigle trial

为直观验证本文算法的跟踪效果,在相同条件下分别采用AI-PHD、GLMB、AI-GLMB算法进行跟踪实验。图2为各算法单次实验结果。可以看出,在高杂波环境下(λ=150),AI-PHD及传统的GLMB算法跟踪性能会衰减,出现目标丢失;而AI-GLMB算法仍能有效跟踪目标。其原因为:PHD基于泊松假设,受杂波影响大,在杂波环境下,AI-PHD虽然采用幅度信息能抑制低幅度杂波的影响,但高幅度杂波仍会影响PHD跟踪性能;GLMB算法基于多假设思想,利用多帧量测信息具有较好的抗干扰性能,但高杂波环境会削弱真实目标权重,导致目标丢失,降低跟踪性能;AI-GLMB算法通过引入幅度信息,改进了似然函数,从而降低了杂波分量的权重,进一步增强杂波抑制能力,相比GLMB算法具有更好的跟踪性能优势。

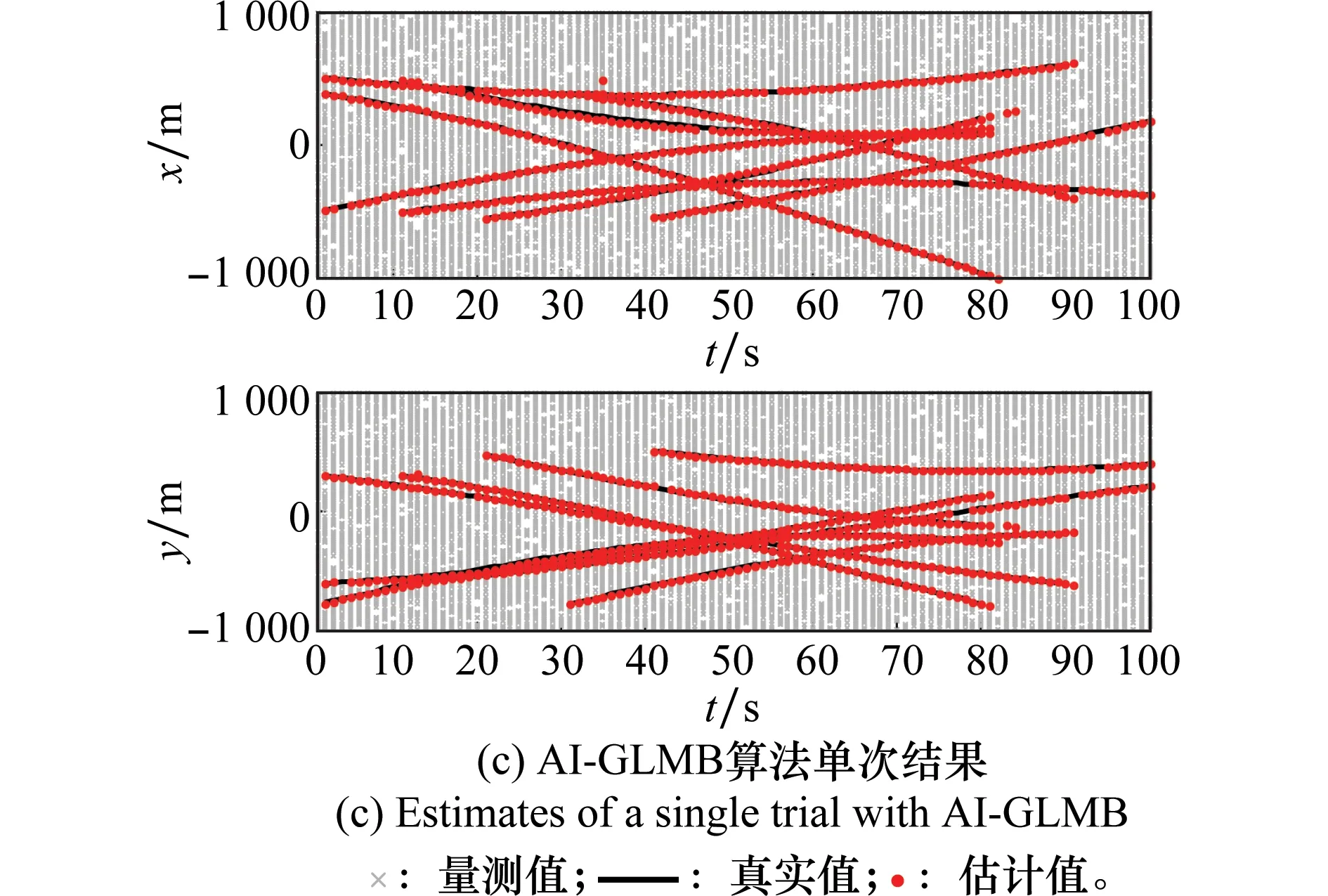
图2 单次实验结果Fig.2 Estimates of a single trial

为比较不同算法的估计性能,分别对AI-PHD、GLMB、AI-CBMeMBer、AI-GLMB算法进行100次蒙特卡罗实验。图3为不同算法势估计方差结果。

图3 势估计方差Fig.3 Variance of cardinality estimates

可以看出:AI-GLMB算法与AI-CBMeMBer算法势估计方差相当,相比AI-PHD及GLMB跟踪算法,方差更小,说明其势估计更稳定。图4为对应的平均最优子模式分配(optimal swb-pattern assignment,OSPA)距离如图4所示。

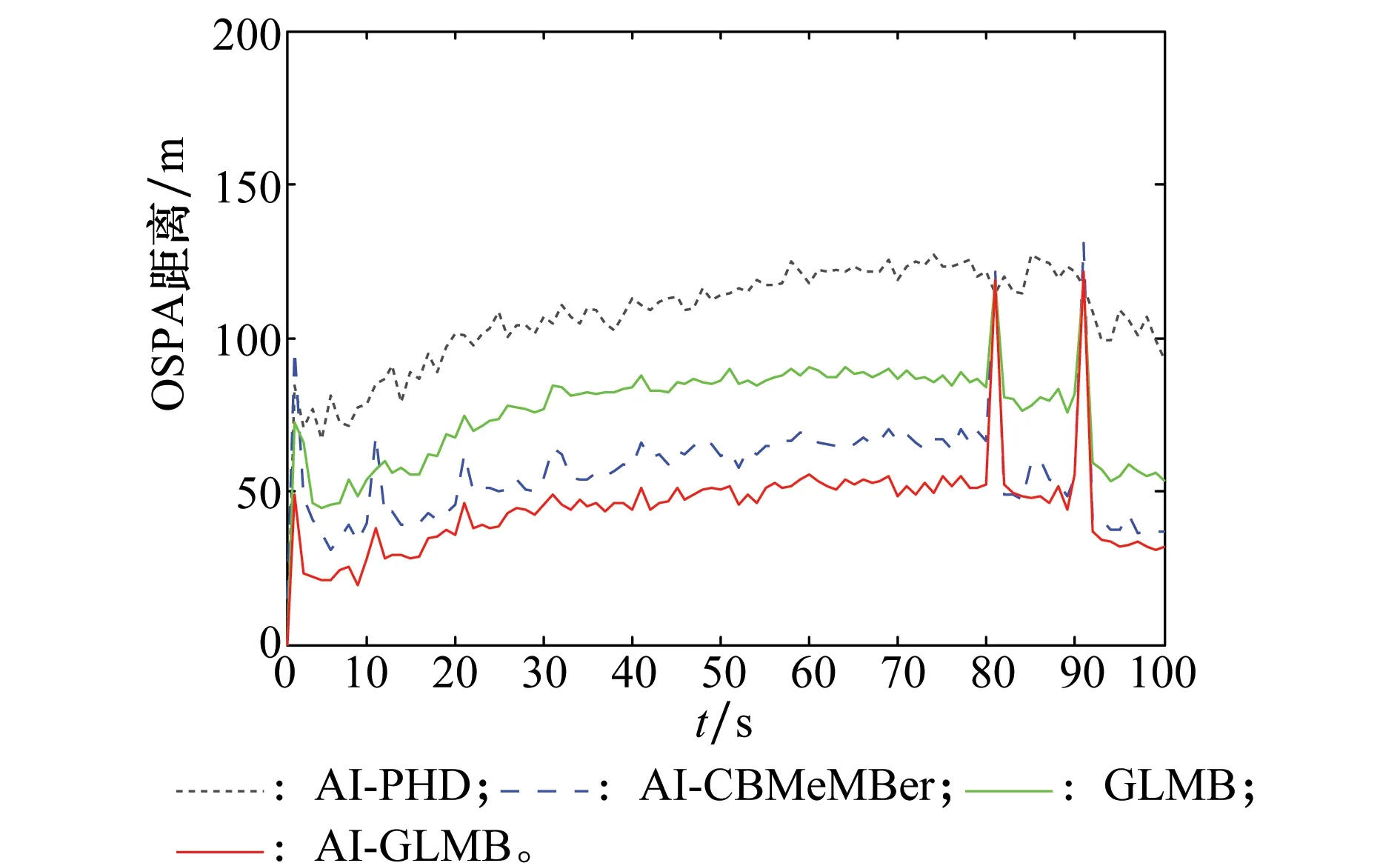
图4 OSPA距离Fig.4 OSPA distance

可知:相比其他3种算法,AI-GLMB算法估计精度最高,这是由于PHD及CBMeMBer滤波器为保证共轭分布,均采用各种近似技术,从而降低了跟踪精度。当目标消失时,同AI-CBMeMBer、GLMB算法类似,AI-GLMB算法会存在目标过估,从而导致其OSPA出现尖峰,对目标消失反应速度较慢。

4 结 论

通常,目标具有较为稳定的AI,而杂波幅度无此特征,因此利用AI可弱化杂波影响,提高跟踪性能。本文通过结合AI的杂波抑制能力及GLMB的抗干扰特性,提出了AI-GLMB滤波器,增强了杂波环境适应性。通过引入AI扩展目标状态,建立幅度似然函数,推导了新的更新方程。针对非线性运动模型,给出了算法的SMC实现方法。仿真结果表明,在强杂波环境下,相比AI-PHD、AI-CBMeMBer及传统的GLMB滤波器,本文算法跟踪精度更高。