基于Laplace先验的复贝叶斯压缩感知ISAR高分辨成像算法
朱晓秀,胡文华,马俊涛,郭宝锋
(陆军工程大学石家庄校区电子与光学工程系,河北 石家庄 050003)
0 引 言
逆合成孔径雷达(inverse synthetic aperture radar,ISAR)具有全天时、全天候、作用距离远和分辨率高等特点,能够获得目标的二维图像,有利于目标分类与识别,在民用和军用领域应用广泛[1]。由雷达成像原理可知,通常采用增加发射信号带宽和增大观测角度范围的方式分别提高距离向和方位向分辨率。在实现ISAR二维成像时,传统的成像算法如距离多普勒(range doppler,RD)算法有一定局限性。一方面,由于ISAR目标的非合作性,为获得方位向高分辨,在观测时间内目标的散射特性可能变化较大[2],利用传统的初相校正方法后不可避免地存在残余相位误差导致图像散焦[3]。另一方面,RD算法实质上是对回波数据进行快速傅里叶变换(fast Fourier transformation,FFT)处理,会产生较高的副瓣影响成像质量,并且对噪声抑制能力不强,在低信噪比(signal-to-noise ratio,SNR)条件下得到的ISAR图像存在较强的干扰噪声。
压缩感知(compressed sensing,CS)理论表明,稀疏信号可由求解l1范数最优化问题得到高概率重构[4]。由于ISAR成像的强散射中心仅占整个成像平面非常少的像素单元,说明具有很强的空域稀疏性[2],这吸引了国内外众多学者研究基于CS理论的ISAR成像方法,并发现利用ISAR图像的稀疏特性可以在提高成像分辨率的同时能有效地降低副瓣和抑制噪声。为解决图像散焦问题,文献[5]在CS理论的基础上提出了一种基于贝叶斯估计的ISAR自聚焦成像方法,将运动误差相位估计和ISAR图像重构转化为l1范数约束问题,通过回波数据矢量化并采用数值迭代方法求解最优化问题实现高精度ISAR成像。文献[6-7]将该方法应用到了稀疏孔径中,实现了稀疏孔径自聚焦高分辨成像。但基于l1范数约束的自聚焦成像方法求解时涉及二维数据矢量化、稀疏字典对角化操作,增加了数据存储量和运算复杂度,且该类算法只利用了目标图像的稀疏特性,有时候不能获得最优稀疏解。文献[8]进一步考虑了目标图像的结构信息,利用图像的联合稀疏先验特征,将ISAR自聚焦成像转化为多测量矢量联合稀疏优化问题,假设目标图像各像元服从复高斯分布,提出了一种基于贝叶斯压缩感知(Bayesian compressed sensing,BCS)的ISAR自聚焦成像方法,进一步改善了自聚焦精度和成像质量。文献[9]表明,在实数域应用联合Laplace分布比Gaussian分布具有更好的稀疏促进作用。但由于ISAR回波信号为复数,采用传统的贝叶斯推理需要将复数转换为实数后进行求解,增加了运算复杂度。
综上所述,现有的算法应用到ISAR成像中存在稀疏效果不强、数据存储量大、运算复杂度高等问题,基于此,本文提出了基于Laplace先验的复(complex BCS,CBCS)ISAR高分辨成像算法。假设目标图像各像元服从复Laplace先验建立稀疏先验模型,直接对复数信号进行贝叶斯推理,并采用分布式计算方法,先逐距离单元求解其对应的目标像,再逐脉冲求解相位误差,在提高成像质量的同时减小了数据存储量和运算复杂度。仿真实验表明,与基于l1范数约束和基于稀疏贝叶斯学习(sparse Bayesian learning,SBL)的自聚焦成像算法相比,本文的算法具有更好的成像效果。
1 信号模型
利用传统的成像算法(如RD算法)实现运动目标ISAR二维成像主要是将回波数据先通过脉冲压缩实现距离向高分辨,再通过目标转动产生的多普勒信息实现方位向高分辨。在进行方位向处理前,需要将目标运动时产生的与成像无关的平动分量进行补偿。假设ISAR回波信号经距离维脉冲压缩之后,已经做过传统的平动补偿处理。由文献[10]可知,包络对齐的精度可以实现小于1/2的距离单元,但相位校正的误差相位补偿精度要求在波长量级,较难达到,因此相位校正后的残余相位误差通常不能忽略,会导致图像散焦,而且在低SNR条件下存在较强的干扰噪声和副瓣,严重影响了成像质量。
ISAR成像时,目标强散射中心虽仅占整个成像平面少量的像素单元,但却贡献了目标散射场的绝大部分能量,说明ISAR成像具有很强的空域稀疏性[2],即可将CS理论应用到ISAR成像中。考虑到噪声和相位误差的存在,基于CS理论的单基地ISAR成像模型的回波数据用矩阵形式表示为[5]
S=EFA+ε
(1)
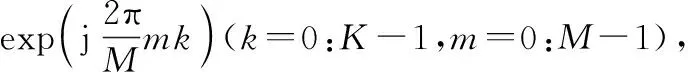
国内外已有不少学者基于CS理论的稀疏重构方法进行了研究,并发现利用ISAR图像的稀疏特性可以有效提高成像分辨率、降低副瓣和抑制噪声[5]。但一般的稀疏重构方法仅从优化的角度进行了高分辨重构,而没有考虑与ISAR图像相关的所有信息,有时无法得到最优稀疏解,重构精度有进一步提高的空间。
2 基于Laplace先验的CBCS ISAR高分辨成像
BCS理论是在CS理论的基础上,充分挖掘和利用目标的先验信息构造信号重构模型,利用贝叶斯统计进行推理,可实现更好的信号恢复效果。由于贝叶斯灵活性高,适用范围广,相比于传统的CS重构算法有一定的优越性,因此本文考虑将BCS理论与ISAR成像相结合,利用ISAR图像的稀疏性和先验信息进行BCS框架建模,并利用相应的重构算法实现图像重构。
目前,在BCS理论重构算法中应用比较广泛的是基于Gaussian先验的SBL算法,即假设目标各像元服从Gaussian先验,通过超参数约束将稀疏先验模型转化为二层概率模型,即可转化为目标像元服从联合Student-t分布,最后能得到具有稀疏系数的解。有研究表明,在实数域应用由Gaussian先验和指数先验共同约束的联合Laplace先验比Gaussian先验具有更好的稀疏促进作用[9]。但其求解方法都是假设处理数据为实数而进行推导的。由于在ISAR成像过程中,雷达接收的回波信号为复数信号,不能直接应用实数域方法进行求解[11],简单解决办法是将复数信号转化为实部和虚部两个部分,然后再分别利用实数域的推理方法进行求解[12],此时,复数模型可变为
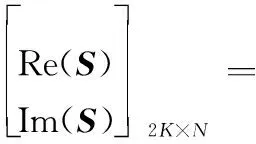
(2)
式中,Re(·)和Im(·)分别表示实部和虚部。可以看出,复数模型转实数模型后,数据存储量变为原来的两倍,运算量也随之增加。而且,由于实部和虚部的重构过程相互独立,存在的估计误差必然会影响其复数相位,进而影响后续的相位自聚焦过程。为避免对复数信号的实部和虚部分别重构,本文假设目标图像各像元服从Laplace先验进行稀疏目标建模,提出了一种直接在复数域处理的基于CBCS的ISAR高分辨成像方法。
2.1 目标图像参数CBCS模型
2.1.1 目标稀疏模型

(3)
对超参数αi可采用指数分布[9]约束,即
(4)
由此,得到新的联合先验为

(5)
式(5)表示像元服从Laplace先验,引入超参数ξ对其中的超参数λ施加Gamma先验分布,即
p(λ|ξ)=Γ(λ|ξ/2,ξ/2)
(6)
采用此分布为了在一定的限制范围内,参数λ的先验分布具有一定的灵活性。
2.1.2 噪声模型
假设ε是复高斯白噪声,其中不同元素为独立同分布随机变量,服从零均值复高斯分布,即其虚部和实部分别独立服从方差为σ2的实高斯分布,则回波信号的条件概率密度函数为
(7)
式中,‖·‖F表示矩阵的Frobenius范数。为获得高斯分布函数的共轭特性,对σ-2施加Gamma先验分布,即
p(σ-2)=Gamma(σ-2|c,d)
(8)

式(5)和式(6)表明,该稀疏先验等价于三级贝叶斯模型,分层模型如图1所示,前两级表示由指数分布和Gaussian分布联合约束的Laplace分布,后一级是对参数λ的约束。所以对像元ai的稀疏先验实际上是通过3层贝叶斯模型ξ→λ→αi→ai依次传递实现的。

图1 CBCS Laplace分层先验模型Fig.1 CBCS Laplace hierarchical prior model
2.2 ISAR高分辨成像求解过程
考虑到回波中不可避免存在平动补偿初相校正后的残余相位误差,将会影响重构算法的性能,进而影响成像质量。因此,有必要结合目标图像稀疏重构和相位误差校正,研究ISAR高分辨成像算法,提高成像质量。由文献[5]可知算法要实现相位自聚焦,就需要利用到完整的回波数据,即每次迭代时必须得到整个二维图像的估计值。传统的算法在实现目标图像重构时采用先将矩阵回波数据矢量化,即将二维回波数据逐距离单元拉直为一维矢量,在每次迭代中利用重构算法实现矢量重构,然后再将重构出的矢量结果转化为二维矩阵形式,即为每次迭代得到的二维目标图像。若采用这种矩阵矢量化处理的思想,式(1)可表示为
(9)
式中,sn、an和εn分别表示第n个距离单元对应的回波矢量、目标图像矢量和噪声矢量。可以看出,回波数据的矢量化、相位误差矩阵和稀疏字典的对角化不仅构造复杂,而且大大增加了存储空间,还会影响后续图像重构时的运算效率。
因此,为避免矩阵矢量化操作,本文在算法求解时提出了分布式计算方法,通过构建新框架,在每次迭代过程中,先逐距离单元利用重构算法处理,将重构结果合成得到二维目标图像后,再逐脉冲处理实现相位误差求解,在一次迭代中就可以实现图像重构和相位自聚焦。这样不用构造复杂的矩阵,减少了数据存储空间,而且在目标图像重构和相位误差求解时相当于每次只处理一个距离单元或一个脉冲的数据,降低了每次的运算量,有效提高了运算效率。本小节将从目标图像重构和相位误差校正两个方面对分布式计算框架的求解方法进行介绍。
2.2.1 目标图像重构
对某特定距离单元数据S·n,其CS模型可表示为
EHS·n=FA·n+ε·n
(10)
式中,EHS·n表示消除相位误差后的数据。
利用式(7)中的条件分布及式(3)、式(4)和式(6)中的稀疏先验信息,根据贝叶斯规则,若给定αn,λ,σ2,其后验分布可分解为
p(A·n,αn,λ,σ2|EHS·n)=
p(A·n|EHS·n,αn,λ,σ2)p(αn,λ,σ2|EHS·n)
(11)
式中,p(A·n|EHS·n,αn,λ,σ2)∝p(A·n,αn,λ,σ2,EHS·n),所以p(A·n|EHS·n,αn,λ,σ2)服从均值为μn,协方差为Σn-λ的复高斯分布[9],即p(A·n|EHS·n,αn,λ,σ2)~CN(A·n|μn,Σn-λ),其中
μn=σ-2Σn-λFHEHS·n
(12)
Σn-λ=(σ-2FHF+Λn-λ)-1
(13)

利用式(11)中的p(αn,λ,σ2|EHS·n)估计超参数αn,λ,σ2。由于p(αn,λ,σ2|EHS·n)=p(α,λ,σ2,EHS·n)/p(EHS·n),故p(αn,λ,σ2|EHS·n)∝p(α,λ,σ2,EHS·n),有
p(α,λ,σ2,EHS·n)=
p(α|λ)p(λ)p(σ2)
(14)
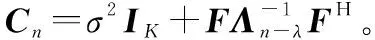
通过最大化联合分布p(α,λ,σ2,EHS·n),可得到αn、λ、σ2的估计,为方便计算,在对数域进行最大化求解,忽略常数项后建立目标代价函数,即
L=lnp(α,λ,σ2,EHS·n)=
(15)
利用行列式恒等式和矩阵求逆公式,并展开最后一项,可得到代价函数为
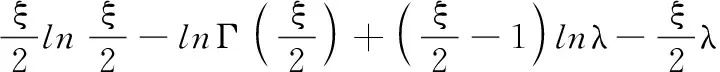
(16)
(17)
由于超参数为正值,求解式(17)后舍去负值根,得到αin的更新公式为
(18)
利用式(16)对σ-2求偏导等于零,可得
(19)
求解式(19)得到σ2的更新公式为
(20)
再利用式(16)对λ求偏导等于零,可得
(21)
求解式(21)得到λ的更新公式为
(22)
为计算简便,令ξ→0,将式(22)代入式(18)可得
(23)
由文献[14]可知,对目标像施加Gausian先验时,αin的更新公式为
(24)
儿童FC主要基于典型的病史和体格检查做出临床诊断,一般不需要其他理化检查。其诊断标准,建议采用罗马Ⅳ标准(以4岁为界分为婴儿/幼儿 FC 和儿童/青少年 FC)[1]、《巴黎儿童便秘术语共识》(PACCT,没有年龄限制)[8]等。
2.2.2 相位误差校正
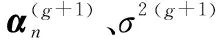
(25)
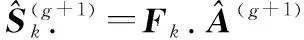

(26)

3 ISAR高分辨成像算法实现流程
利用基于Laplace先验的CBCS ISAR高分辨成像算法实现ISAR成像的流程图如图2所示,具体求解步骤如下:
步骤1ISAR原始回波经脉冲压缩,并做包络对齐和初相校正后得到可能包含残余相位误差的二维回波数据S;
步骤2构造稀疏基字典F,初始化超参数αin=1,σ2=0.01,初始化E=IK,g=1,设定总迭代次数G和门限eps;
步骤3利用相位误差矩阵E进行回波数据相位误差补偿,得到补偿后的回波数据Scom=EHS,即进入图像迭代过程;
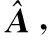
图2 基于Laplace先验的CBCS ISAR自聚焦成像算法流程图Fig.2 Flow diagram of autofocusing algorithm for ISAR imaging based on complex BCS using Laplace priors
4 算法运算量分析
为了更好地比较算法的计算量,本节将进行所提算法的分布式计算方法和矩阵矢量化操作计算方法的运算量分析。以一次加法或乘法为计算量单位,分析每次迭代过程中两种不同求解方式的计算量。
若采用矩阵矢量化操作进行求解,式(9)表示的矢量化后成像模型可重写为
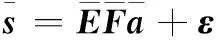
(27)

若利用分布式计算框架逐距离单元进行目标图像重构,对某一个距离单元处理时,F是K×M矩阵,Λn-λ和Σn-λ是M×M矩阵,E是K×K矩阵,S·n是K×1矩阵,则σ-2FHF的计算量为O(KM2),Σn-λFHEHS·n的计算量为O(KM2+MK2+MK),所以根据式(12)和式(13),更新Σn-λ的计算量为O(M3+KM2),更新μn的计算量为O(KM2+MK2+MK),则本文算法一次迭代中处理N个距离单元实现目标图像重构的总计算量为O(NM3+2NKM2+NMK2+NMK),与矩阵矢量化操作求解时的O(N2(NM3+2NKM2+NMK2+MK))相比要小很多,可以有效减少运算量,提高运算效率。
5 仿真实验与分析
通过仿真实验从运算时间、相位误差形式和回波SNR 3个方面对本文算法性能进行验证。运行时间可以反映算法的运算复杂度,体现算法的运算效率;不同形式的相位误差和不同的SNR会影响迭代的收敛性,进而影响图像的聚焦效果,特别是低SNR条件下对算法性能要求比较高,否则无法得到良好的聚焦图像,所以验证本文算法的运算时间以及在不同相位误差形式和不同SNR条件下的自聚焦性能是必要的。
本文仿真实验环境为Windows 7 64位操作系统,Matlab 2016A软件平台,仿真所用计算机主要参数如下:处理器为Intel酷睿i5-6200U,主频为2.30 GHz,内存为4 GB。
5.1 算法运算时间验证

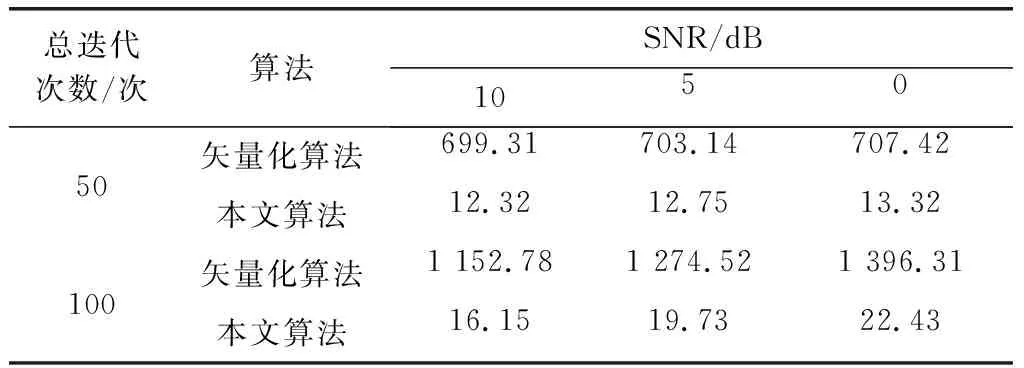
表1 算法运行时间比较Table 1 Comparison of algorithm run time
从表1中数据可以看出,当预设总迭代次数为50次时,相同SNR条件下本文算法的运行时间明显比矢量化求解算法短,说明了本文算法在提高运算效率方面有明显的优势,但由于预设的迭代次数较少,算法无法提前达到收敛条件,两种算法均迭代了50次,故在不同的SNR条件下同一种算法的运算时间较为相近;当预设总迭代次数为100次时,算法能提前达到收敛条件停止迭代,对于同一种算法,随着SNR的增大,运算时间有所减少,说明SNR会影响算法的迭代次数,进而影响其运算时间。
5.2 不同相位误差形式下算法自聚焦性能验证
通过构建简单的理想散射点目标模型验证算法的自聚焦性能。模型如图3所示,目标一共由14个散射点组成,每个散射点幅度均为1。

图3 理想散射点目标模型Fig.3 Target mode of ideal scattering points
为减小运算复杂度,假设回波数据一共有32个脉冲序列且每个脉冲包含32个距离采样单元,迭代次数为100次。为回波数据添加3种不同形式的相位误差,以验证不同形式运动条件下算法性能。第1种为二次相位误差,主要用于分析由高速运动引起的相位误差时算法的性能;第2种为正余弦相位误差,主要用于分析由复杂运动引起的相位误差时算法的性能;第3种为随机相位误差,主要用于分析在由其他不定因素引起的相位误差时算法的性能。图4的每行分别表示二次相位误差、正余弦误差和随机误差条件下的成像结果,其中第1列表示3种不同形式的相位误差,第2列表示添加相位误差后的RD算法直接FFT成像结果,第3列表示本文算法的成像结果。

图4 不同相位误差形式下的自聚焦性能验证Fig.4 Verification of autofocusing performance in different phase error forms
可以看出,在3种不同相位误差形式下,本文算法都有良好的聚焦性能,说明该算法的适用性较强,应用时不用考虑相位误差的具体形式。
5.3 不同SNR条件下算法自聚焦性能验证

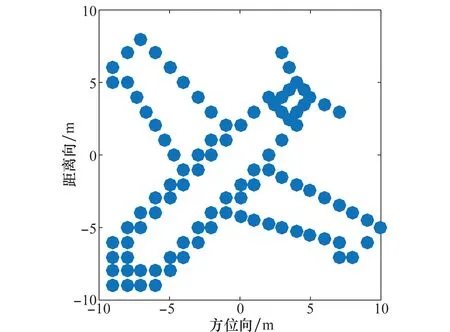
图5 目标飞机仿真模型Fig.5 Simulation model of target aircraft
为方便直观比较算法性能,采用目标背景比(target-to-background ratio,TBR)[14-15]、相位误差提取精度ρ和图像熵En作为衡量标准,其定义可表示为
(28)
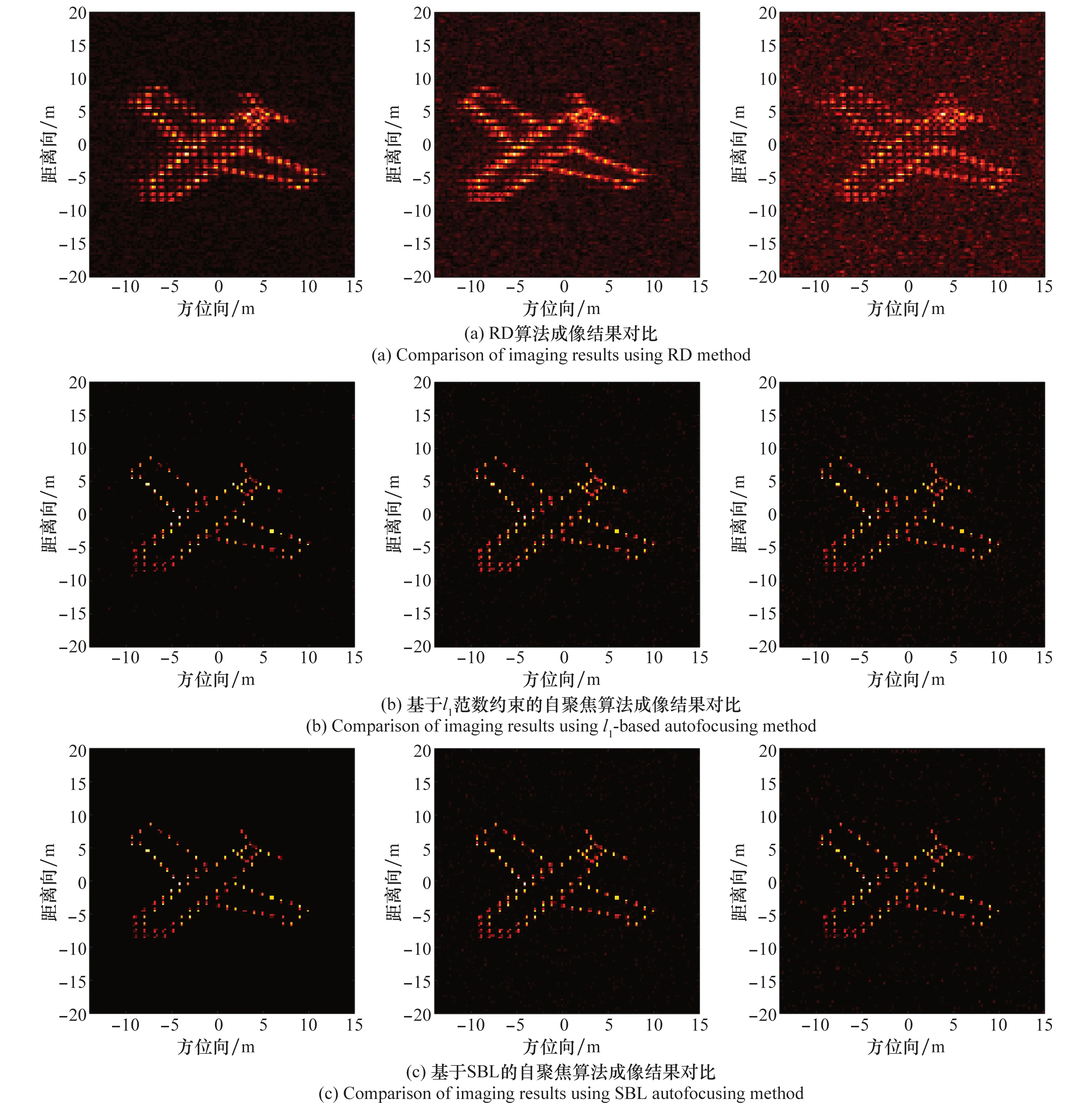
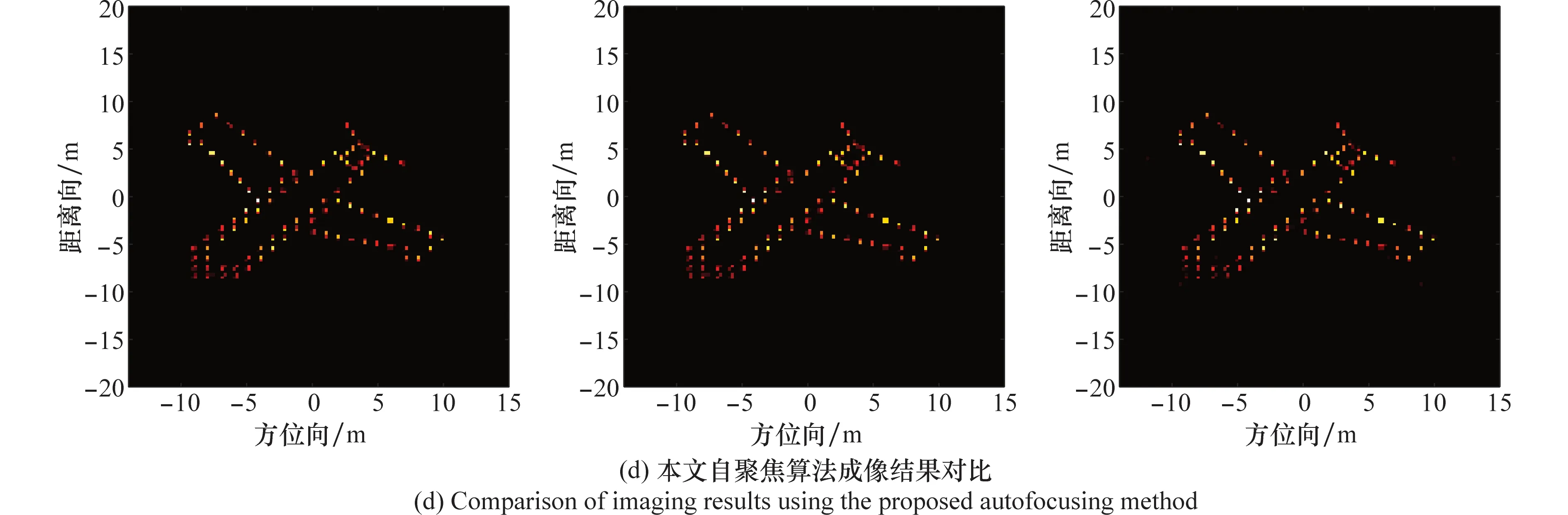
图6 不同算法在3种SNR下成像结果对比Fig.6 Comparison of imaging results using different methods under 3 different SNRs
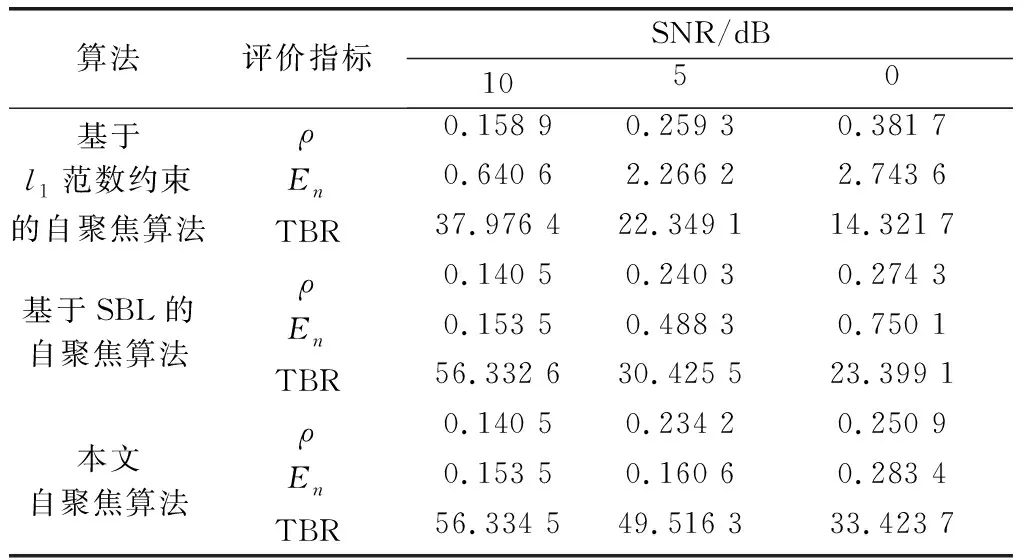
表2 不同算法在3种SNR下评价指标对比Table 2 Comparison of evaluating indicators using different methods under three different SNRs
可以看出,在SNR较高时,3种算法均能较好地实现自聚焦,但随着SNR降低,基于l1范数约束的自聚焦算法对噪声抑制效果不佳,比基于BCS框架下的两种算法成像质量差,有较多的虚假点存在;对比基于SBL的自聚焦算法和本文算法成像结果数据可以看出,随着SNR降低,本文算法的TBR大于SBL算法,图像熵小于SBL算法,同时相位误差提取精度也优于SBL算法,说明本文算法鲁棒性更好,能够在提高图像自聚焦性能的同时有效实现噪声抑制。由于SBL算法是基于Gaussian先验实现的,这也说明了Laplace先验比Gaussian先验有更强的稀疏促进作用。
6 结 论
本文利用ISAR图像的稀疏先验信息、整体结构信息以及噪声模型统计信息,提出了基于Laplace先验的CBCS ISAR高分辨成像算法,在目标图像重构的同时实现相位误差更新。相比于Gaussian先验和传统的稀疏先验模型(如l1范数约束),该算法有更强的稀疏促进作用。在求解过程中,直接对复数信号进行贝叶斯推理,采用分布式计算方法将距离维和方位维分开处理进行求解,减小了数据存储量、降低了运算复杂度,并进一步提高了成像质量。仿真实验表明,在不同相位误差形式和低SNR条件下,该算法都有良好的自聚焦性能。

