案例教学法在自动控制原理教学中的应用
王立红
(辽宁工业大学 电气工程学院,辽宁 锦州 121001)
自动控制原理是辽宁工业大学自动化专业、电气工程及自动化专业和测控技术与仪器专业非常重要的一门技术基础课,是后续专业课程的基础,其教学质量的好坏直接影响后续专业课的教学效果;同时,该课程也是许多高校控制理论与控制工程专业研究生学习专业课的基础。所以,无论是在本科教学,还是在研究生教学领域,自动控制原理都占有相当重要的地位[1-3]。古典控制理论以拉氏变换为数学工具,研究单输入单输出线性定常系统,内容主要包括控制系统数学模型的建立、时域分析法、根轨迹分析法、频域分析法、线性系统校正、非线性系统分析和采样控制系统分析。自动控制原理课程理论性和实用性较强,内容抽象、覆盖面广,公式繁多、计算复杂,要求学生具备较好的定性分析、定量估算、综合运用和数形结合能力,并具有扎实的数学基础。因此,大部分学生在学习过程中经常会感到困难而丧失学习的兴趣,影响学习效果[4-5]。
1 案例教学法的优点
传统的教学方法以教师和教材为中心,注重规范性,轻视创新性,课堂上大多数时间是教师讲学生听,教师写学生记,教师问学生答,教师是知识的传授者,学生是知识的被动接受者。虽然教师的教学逻辑严密,但是学生在学习过程中没有针对性,目的不明确,感到枯燥乏味,丧失了学习的主动性和积极性,课堂效率低下[6-7]。案例教学法与传统教学法相反,通过具体实例再现理论,变抽象为具体,把复杂问题简单化,学生从具体问题出发,通过分析和思考,寻求解决问题的途径,探索方法的合理性和科学性,从而对抽象理论的理解更加具体和深刻[8-9]。案例教学法通过一个典型实例讲授一套完整理论中的各个知识点,以揭示各个知识点之间的相互关系,使学生对前后知识有效衔接,学习起来得心应手,不再会因为枯燥的理论和复杂的计算而感到困惑。学生在一个个教学案例的驱动下,紧跟教师教学思路,积极探索,努力创新,课堂气氛活跃,教学效果显著改善。
2 课堂教学知识点举例
中国电力出版社出版的 《自动控制理论》第4章时域分析法的第5节是控制系统的稳定性分析[10],假设描述系统的微分方程为:
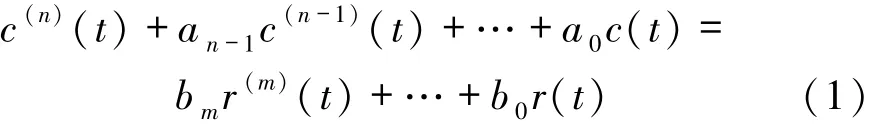
对式(1)进行拉氏变换得:

简写为:

式中,M(s)=sn+an-1sn-1+…+a0是传递函数的分母多项式,N(s)=bmsm+bm-1sm-1+…+b0是传递函数的分子多项式,R(s)为输入,C(s)为输出。传递函数G(s)可写为:

假设M(s)有n个互异极点si(i=1,2,…,n),根据代数基本定理,闭环n次方多项式都可以拆解成n个1次因子多项式,即:

所以一个n阶系统可以分解成n个一阶子系统,即得到n个子模态。下面对一阶系统特征值的模态进行分析。
假设一阶系统的传递函数为:

单位阶跃输入下系统的输出为:
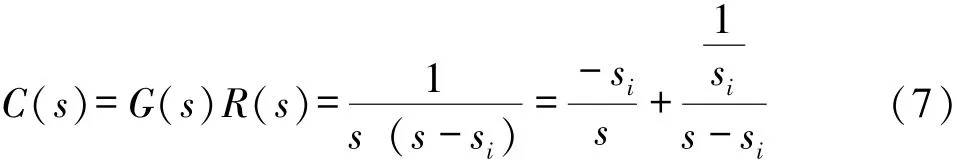
对式(7)进行拉氏反变换,得

1)当si为实根时,即si=σi,有:

对应的响应曲线如图1所示。

图1 si为实根时系统的稳定性
由图1可见,当系统的特征根为负数时系统稳定;当系统的特征根为零时系统临界稳定;当系统的特征根为正数时系统不稳定。
2) 当si为共轭复根时,即si=σi±jωi,有

当

对应的响应曲线如图2所示。

图2 si为共轭复根时系统的稳定性
由图2可见,当特征根的实部为负数时,输出响应曲线呈衰减振荡,最终趋于稳态值,系统稳定;当特征根的实部为零时,输出响应曲线呈等幅振荡,系统临界稳定;当特征根的实部为正数时,输出呈发散振荡,系统不稳定。
通过上面的知识点讲解可以发现,通过分析闭环传递函数极点的性质就可以判断系统是否稳定;但是这种教学方法理论性较强,内容抽象,理解起来比较困难,学生会感到枯燥乏味,学习积极性不高。如果能在教学中引入具体的案例,通过MATLAB仿真分析,可以使学生简单直观地掌握该知识点,而不用纠结于数学推导和理论分析,从而激发学生的学习兴趣,改善教学效果[11-12]。
3 课堂教学案例的引入
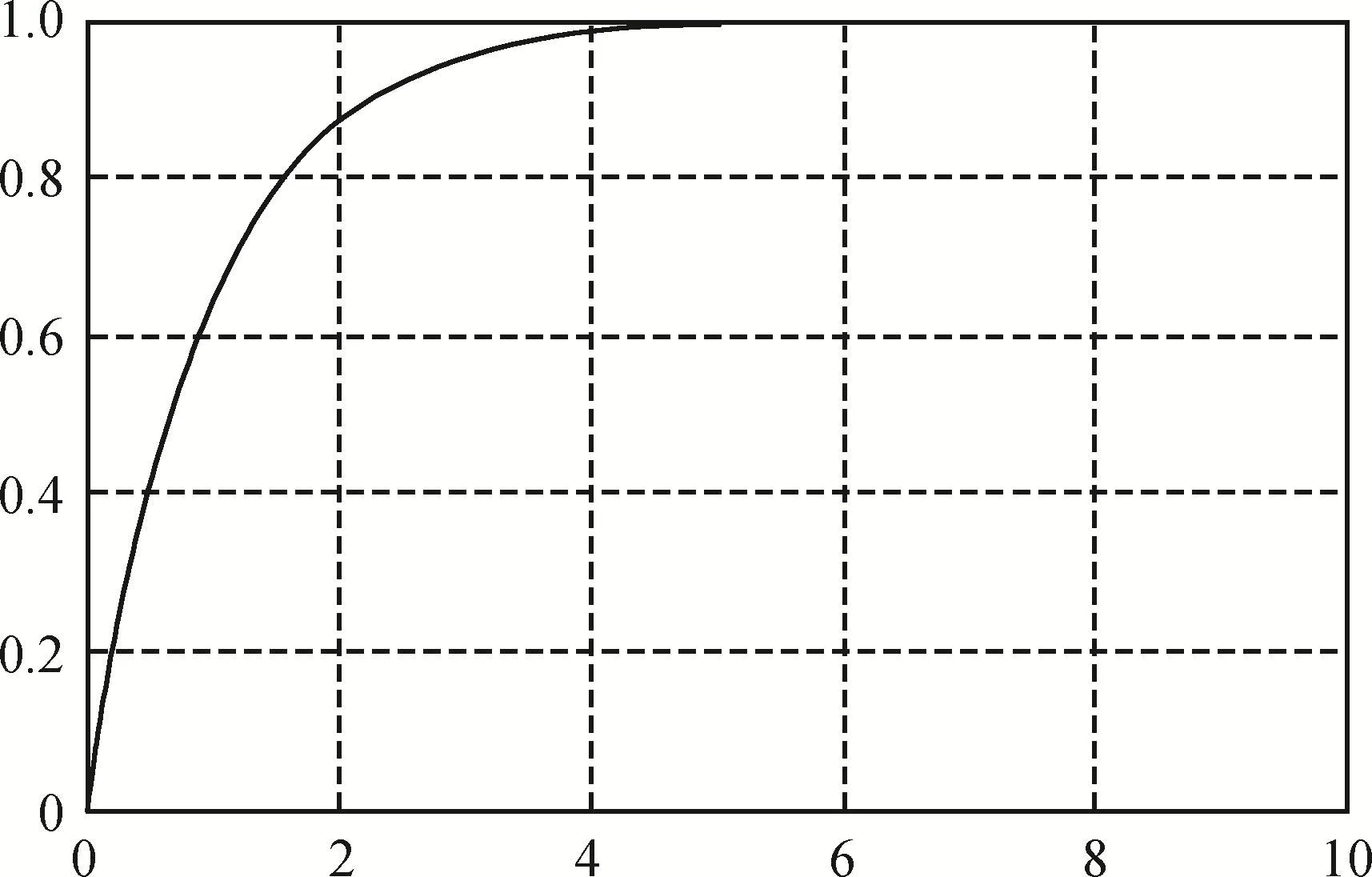
图3 si=-1时系统的单位阶跃响应
当si=1时系统的单位阶跃响应如图4所示。由图可见,系统的输出曲线呈发散状态,无法稳定在稳态值上,因此系统不稳定。
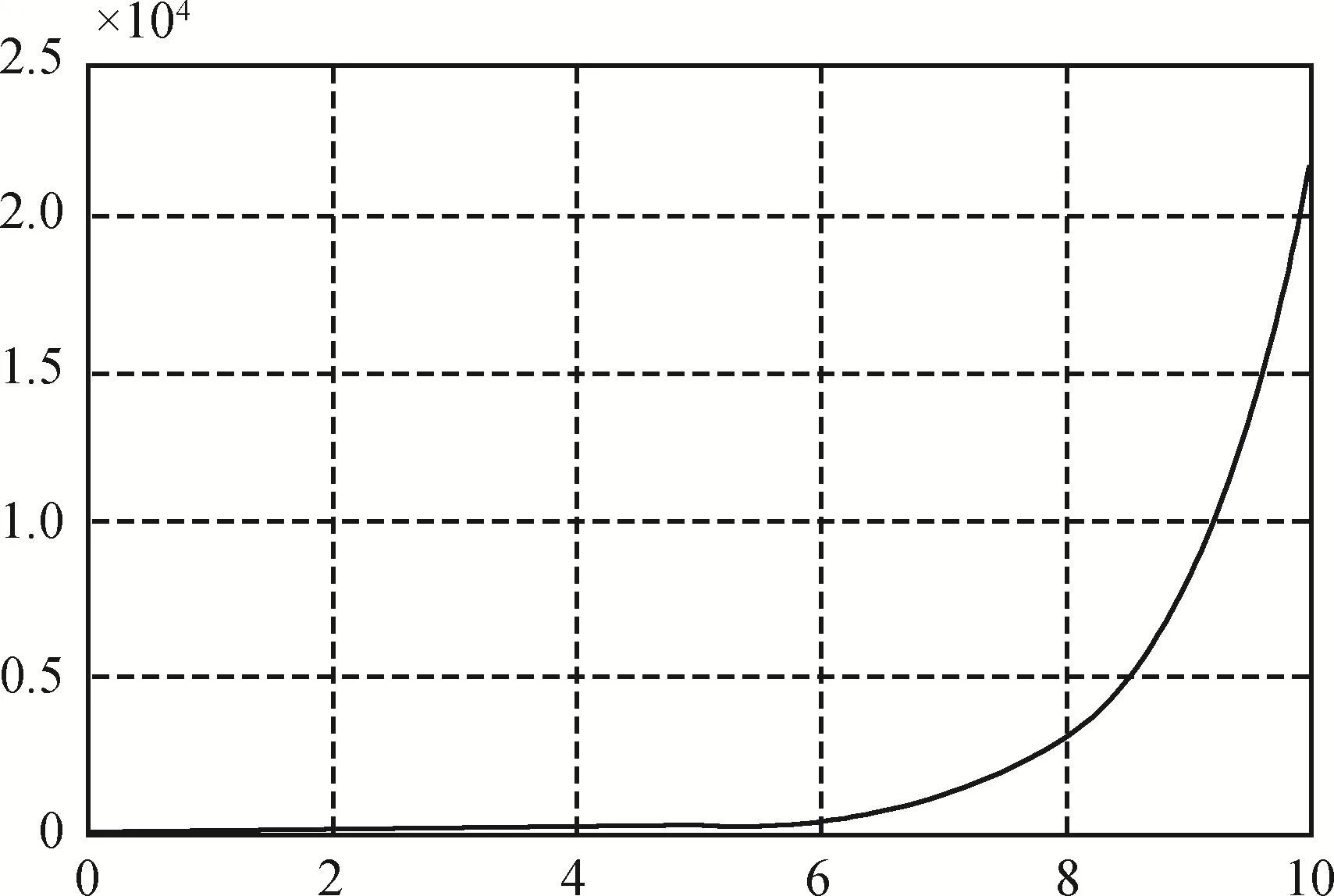
图4 si=1时系统的单位阶跃响应
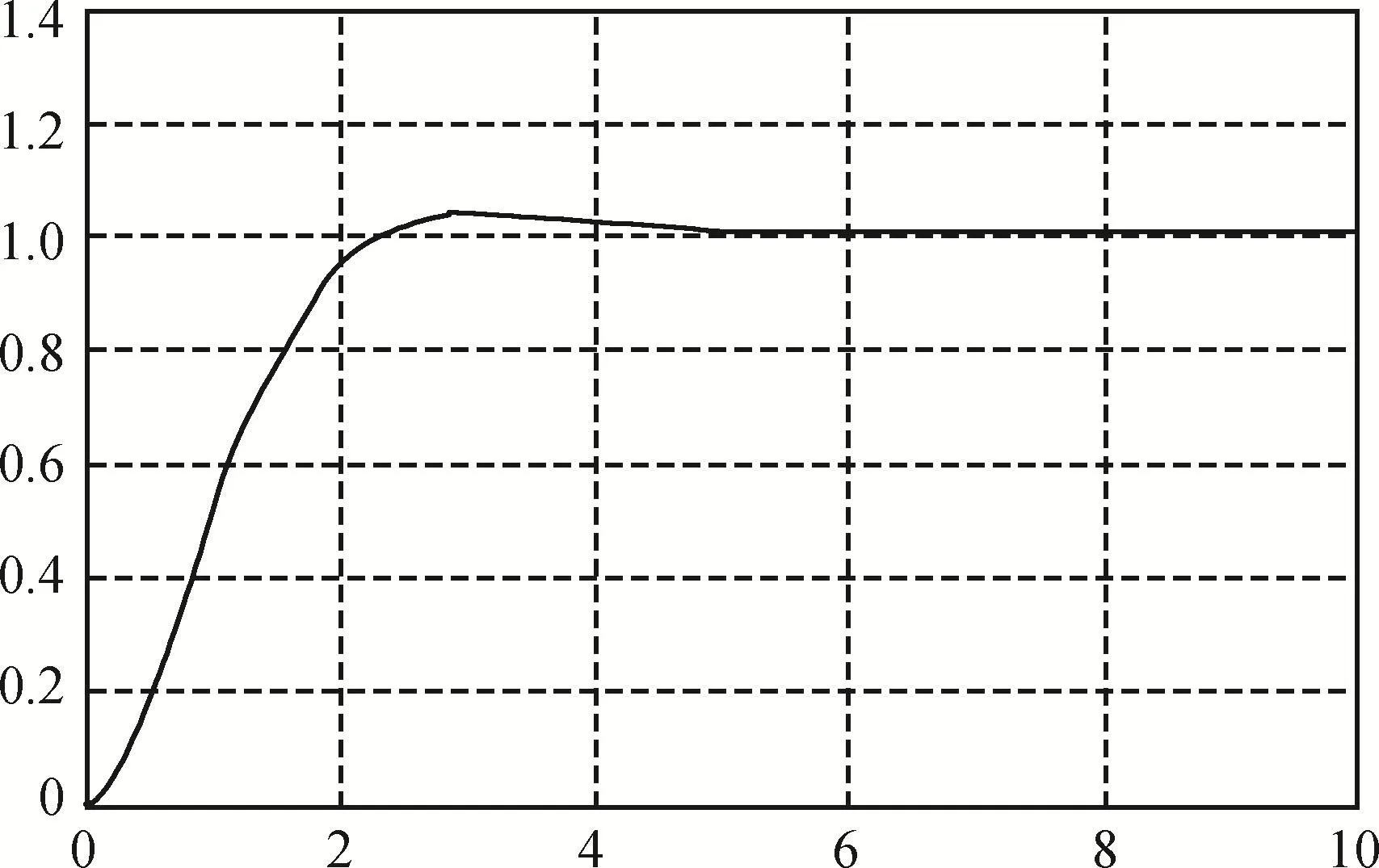
图5 特征根实部为负时系统的单位阶跃响应

图6 特征根实部为正时系统的单位阶跃响应

图7 特征根实部为零时系统的单位阶跃响应
4 结束语
在自动控制原理课堂教学中采用案例教学法,与传统教学方法相比较,更容易调动学生的积极性和主动性,激发学生的学习兴趣,培养学生分析问题、解决问题和综合应用能力,提高课堂听课效率,改善教学效果。

