基于单目标优化的众包任务定价模型

王依凡，叶宏达，邱子杰，王志勇

(1.电子科技大学 计算机科学与工程学院,四川 成都 611731；2.电子科技大学 信息与通信工程学院,四川 成都 611731；3.电子科技大学 数学科学学院,四川 成都 611731)

随着 “互联网＋”时代的到来,多家公司基于移动互联网建立自助式劳务众包平台,“拍照赚钱”是其中一种自助式大众外包服务模式。用户注册成为APP会员后,在APP上领取需要拍照的任务,从而赚取任务所标定的酬金。这种新型的众包任务平台运营模式,扩大了资源范围,提高了原本的工作效率,形成以大众网络为核心的独特竞争力的运行系统[1-2]。而在众包的任务设计过程中,如何保证任务的有效完成以及激励用户继续接单任务的意愿度,成了一个重要的问题。通常,众包平台会采用提升任务价格或是将几个任务打包成一个任务的方式来刺激接单。而在研究目前的众包价格规律中,大多数采用了多元线性回归的方法来分析价格规律[3-5],或采用Logistic回归模型结合线性回归分析价格规律[6]。

本文根据 “闲侠拍立赚”众包平台的数据,综合考虑了区域的经济水平、人民生活水平和时间成本、人均任务数等因素,研究众包任务的定价规律。在设定新的定价方案时,进一步考虑了众包平台的收益,建立以任务定价为决策变量,以众包平台利润的限度为约束条件,以任务完成率最大化的单目标优化模型进行求解,并通过任务完成率和用户信誉度的提升率对新旧方案进行比较；再进一步考虑实际情况下,众包平台将位置比较集中的任务联合一起打包发布,利用用户的价格效用感知价值规律对原模型进行修正；最后利用蒙特卡洛算法模拟了新方案的实施效果。

1 问题分析

为研究目前众包平台的任务定价规律,本文根据 “闲侠拍立赚”众包平台的数据,包括任务经纬度坐标、任务标价和任务完成情况,以及会员的经纬度坐标、会员预定任务限额和会员信誉值等信息,在MATLAB中绘制已完成任务和未完成任务的热力分布图,如图1所示。

图1中圆圈表示已完成任务,叉表示未完成任务。根据该已完成任务和未完成任务的热力分布图可知,两者的分布具有较强的空间区域特性,因此可采用K-Means聚类算法和网格法对经纬度进行区域划分。为了较好地概括反映空间区域特性,同时具体反映各区域的情况,以0.02°为步长,分别对经纬度进行划分,将经度在112.6°E～114.6°E, 纬度在22.4°N ～24.4°N 的区域划分成100×100的网格,其中纬度每改变0.01°N,实地距离约改变1.849 1 km；经度每改变0.01°E,实地距离约改变1.855 3 km[7]。

图1 已完成任务和未完成任务的热力分布图

根据经济学规律,研究任务定价规律,一方面可通过任务所在经纬度位置的会员密度与任务之间的供需比进行分析；另一方面,任务的自身难度可能对任务的定价产生影响,可通过该任务与相同会员密度任务的定价均值进行比较,确定任务自身的难度系数,对任务定价规律进行修正。

2 任务定价规律的求解模型

2.1 任务定价规律与会员密度的关系

对经纬度划分的每个网格进行编号,可统计每个网格内的任务总数,记为λDi(i＝1,2,3,…,10 000)。同时考虑到,众包会员的活动范围有一定的限制,因此假设每个众包会员存在接受任务的意愿距离为R。以每个任务为圆心,意愿距离R为半径画出可行圆,经纬度范围在可行圆中的会员数即为可完成此任务的意愿会员数。根据蚂蚁众包、阿里众包和美团众包等众包平台公司的使用数据,众包会员的意愿距离R范围大约在3.5～4.0 km,参考网格法划分的网格实际距离,对任务所在网格四周所在的九宫格内的众包会员总数进行统计,周围众包会员总数记为Si。定义区域i的会员密度为:

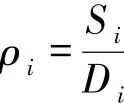
利用MATLAB中的Curve Fitting Tool曲线拟合工具箱对任务j的定价pj与任务的周围会员密度ρi进行函数拟合,除去数据中异常值后,对拟合后函数与实际定价进行残差计算,求解出残差最小的函数形式,进而得到任务定价p与任务的周围会员密度ρ的具体函数表达式p＝f(ρ)。

针对拟合后的函数与实际任务定价p之间存在较大差异的个别点,这些点所对应任务的实际定价与相同会员密度的任务定价存在明显差异,可假设相同会员密度的任务定价呈正态分布,通过3σ原则筛选出奇异点(σ为标准差)。

对于定价超过均值上下3σ范围内的任务,可能是任务本身难度系数存在差异[7],因此定价出现偏差,可通过引入任务难度系数η对定价p的函数表达式进行修正。

针对筛选出的奇异点所对应的任务,定义其难度系数为:

式中,ηj为任务j的难度系数,j为任务j的实际定价,pj为任务j根据式p＝f(ρ)的理论函数值。对定价p的函数表达式通过难度系数η进行修正,修正式为:

2.2 任务完成率的模型建立

考虑到任务完成程度的分布具有显著的地域性特点,因此可通过K-Means聚类算法根据任务完成率对经纬度进行聚类。设一组经纬度数据为{(lo1,la1),(lo2,la2),(lo3,la3),…,(lon,lan)},其中lo为经度,la为纬度,n为完成任务的总数,同时根据热力图给出聚类中心的经纬度初值{(co1,ca1), (co2,ca2), (co3,ca3),…,(co4,ca4)},利用K-Means聚类算法,以每个任务的经纬度数据与离它最近的聚类中心的欧式距离平方和最小为优化目标函数[8],目标函数定义如下:

根据上述K-Means聚类算法将区域划分为4个片区,记为Q1,Q2,Q3和Q4。根据上述模型分析可知,影响任务完成率的因素主要有人均任务数、任务定价、人均预定任务限额以及地域属性等,其中人均任务数、任务定价、人均配额决定了众包软件平台的人均利润,第i个聚类区域的人均利润计算公式为:

而众包平台会员在选择任务的过程中不仅受到人均利润的影响,还与当地的经济水平有关,在经济较发达的地区,生活成本与时间成本相对较高,相同的利润对会员接受任务的吸引程度较弱；在经济欠发达的地区,生活成本与时间成本相对较低,相同的利润对会员接受任务的吸引程度较显著。

对于地区的生活成本与时间成本通过人均工资[9]进行衡量,可进一步定义指标接受任务意愿度为:

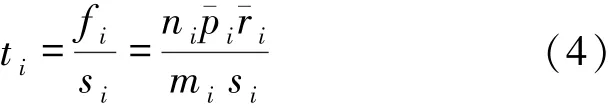
式中,ti为第i个聚类区域的接受任务意愿度,si为第i个聚类区域的人均工资。

利用SPSS对各聚类区域的任务平均完成率与综合指标意愿度之间的线性关系进行检验,任务平均完成率定义为:

式中,uj为第i个聚类区域的任务平均完成率,uij为经纬度在第i个聚类区域的第j个任务的完成情况,ni为第i个聚类区域的任务总数。

2.3 任务定价规律的求解结果与分析

通过MATLAB的cftool工具,求解出任务定价p与周围会员密度ρ的拟合关系表达式为:

在对求解结果的误差分析中,发现拟合函数关系得到的定价理论值与任务实际定价存在个别奇异点,根据2.1节中对难度系数的修正,修正后的定价规律p′表达式为:

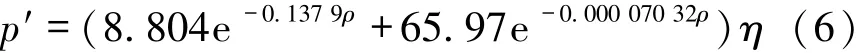
式中,ρ为周围会员密度,η为难度系数。

对于修正后的定价规律,对所有网格的任务进行相对误差的计算,求得的相对误差平均值为0.935 4%,相对误差平均值较小,说明拟合结果较好。

同时根据修正后的定价规律分析易知,定价规律主要与周围会员密度以及任务的难度系数有关,周围会员密度越大,定价的价格越低,说明周围众包任务会员数量越能满足任务的需要,出现供过于求的情况。另一方面,难度系数越高,价格越高,说明难度越大的任务,越需要通过价格提高来鼓励会员接受任务。

利用SPSS对各聚类区域的任务平均完成率u与综合指标意愿度t之间的线性关系进行检验,得到表达式(且拟合精度的平均值约为85.70%)为:

针对上述聚类得到的区域参数与完成度如表1所示。

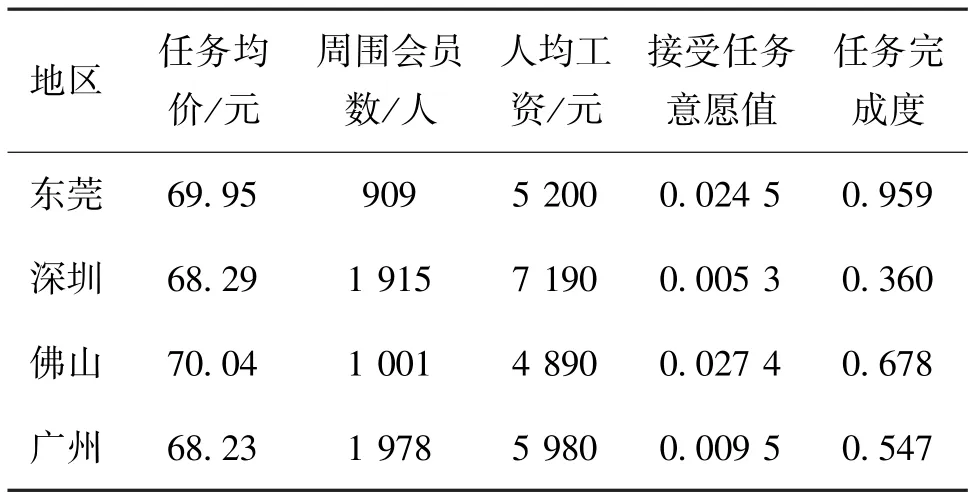
表1 区域完成度与相关因素表

分析完成率的函数表达式与表1可知,如对于区域完成度较低的深圳地区,人均工资越高,完成率越小,说明在时间成本与生活成本较高的地区,相同的任务定价对用户的吸引程度下降,用户的接受任务意愿度下降。

3 优化的任务定价方案

3.1 众包平台可持续性与任务定价的关系

在对任务定价的过程中,除了考虑到任务定价对众包平台用户任务完成度的影响,还需考虑众包APP自身的可持续发展问题,可通过众包平台的利润进行衡量。

假设对于每个已完成任务,众包平台以原价的β倍作为利润进行定价,则对第i个区域众包平台的总营业额为:

式中,ni为第i个区域任务总数,β为每个任务的利润比例,pi为第i个区域的任务定价。

对第i个区域众包平台的总损失额为:

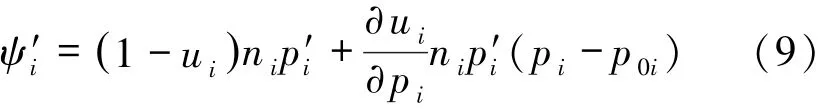
式中,ui为第i个区域任务完成率,pi为第i个区域的任务定价,p′i为第i个区域未完成任务的定价,p0i为第i个区域的初始任务定价。第一项表示由于任务未完成造成的损失金额,第二项表示由于价格变动对任务完成率改变造成的损失。

故对第i个区域众包平台的利润值的计算为:

3.2 以任务定价为变量的目标优化模型

在制定任务定价的新设计方案时,众包平台通常以任务完成率为主要目标,而在一定限度内适度降低自己的利润,设定众包平台降低利润的最大限度为原利润的80%,可建立以任务定价为决策变量,以众包平台利润的限度和任务定价的范围为约束条件,以任务完成率ui为目标建立优化模型,模型如下所示:

式中,ti、φi和φ0i分别为第i个区域的接受任务意愿度、众包平台的利润值和原利润值。

考虑任务难度系数,根据上述模型求解出的各区域的任务定价均值,对于每个任务,即经度为loj,纬度为laj的任务j,在新的定价设计方案下的pj值为:

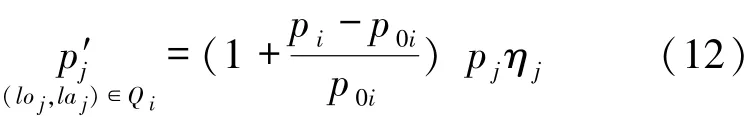
3.3 打包情况下的模型修正

首先考虑对位置较集中的任务进行打包,基于模型一中以经纬度0.02°为步长划分的网格,统计每个网格的任务数量,并对所有网格任务数量求均值,即:

考虑在经度方向约1.855 3 km,纬度方向约1.849 1 km的网格内,任务之间的相对位置较集中,对网格内的任务进行联合打包发布,故打包个数x为向下取整,即x＝｜¯｜。

根据文献[10-11]可知,基于市场经济学理论,销售单价与商品包装的相对数量之间存在一定函数关系,可得众包平台问题中,相对单个任务的定价与打包内任务的个数之间的函数关系为:

式中,y为相对单个任务的定价,x为打包任务的个数。

根据文献[12]可知,对于众包平台用户,众包平台为了扩大市场份额,提高用户接受任务的积极性,销售单价相对较低,而用户的效用感知价值也会产生变化,用户的效用感知价值定义为:

式中,p为任务打包前定价,y为相对单个任务的价格。

在任务完成率的求解过程中,可通过用户的效用感知价值 p′对完成率的计算公式进行修正,即:

式中,n、m、w和s分别表示在网格所属的聚类区域的任务人数、会员人数和人均工资。

将修正后的用户效用感知价值代入众包平台利润值φi的计算中,应用在目标优化模型式(10)中,可求解得出打包情况下的定价方案。

4 求解结果

4.1 目标优化模型的新方案求解结果

通过3.2节中的目标优化模型求解出新方案的任务定价,将新定价方案与原方案进行对比,对比结果如表2所示。

表2 各区域新旧定价方案的任务完成率的变化

通过MATLAB的cftool工具拟合得到众包平台用户的信誉值λ与人均预定任务限额¯ri的函数关系为:

经SPSS检验可得,式(14)中人均预定任务限额可表示为:

式中,ni、mi和pi分别为第i个区域任务总数,用户总数和任务定价均值。通过式(16)可预测新定价方案下众包平台会员信誉度的变化,如表3所示。

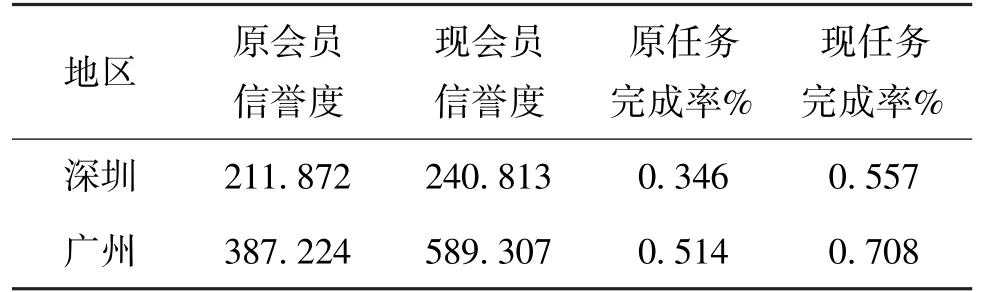
表3 原定价方案与设计定价方案的效果对比

由表3可得,新定价方案与原定价方案相比,大多数地区任务完成率和会员信誉度有所提高,说明对于众包平台的客户而言,任务完成率提高有助于提高众包平台的客户数量；对于众包平台的用户会员而言,会员信誉度的提高有助于会员对众包平台的忠诚度增加与接单积极性的提高。

4.2 打包情况下新定价方案的模拟效果

通过蒙特卡洛法模拟区域任务完成度,得到原定价方案与设计定价方案的完成度热力分布对比图如图2和图3所示(其中圆圈表示已完成任务,画叉表示未完成任务)。

图2 原方案任务完成度

图3 新方案任务完成度

由图2和图3对比可以看出,根据本文考虑打包情况下对任务完成率进行优化的定价方案,与原方案相比,任务完成度整体提高,特别是对于图中左上角所对应的广州和右下方的深圳地区,原本画叉区域较大,说明原方案下未完成率较高,在本设计定价方案下,圆圈图样较密集,说明完成率极大提高。

5 结束语

本文通过网格法和K-Means聚类算法对众包平台的数据进行处理,分析得出众包任务的定价规律,既保留了原始数据的区域特征,又在一定程度上降维简化计算过程。基于单目标优化模型求解得到新的定价方案,从众包任务完成率、众包平台自身利润和平台用户信誉度多个角度对新旧定价方案效果进行量化评价。借用经济学中用户感知价值概念对打包情况下的定价方案进行修正,通过蒙特卡洛法模拟出新方案的实施效果。

在实际情况下,众包任务的打包是一个动态过程,定价方案会随着打包情况改变,本文仅对此进行静态分析,此问题有待后续探究解决。