基于卷积反投影的CT系统参数标定和成像模型

王誉儒，杨玉聪，官 庄，王志勇

(1.电子科技大学 英才实验学院,四川 成都 611731；2.电子科技大学 数学科学学院,四川 成都 611731)

电子计算机断层扫描(CT)系统成像如今在医疗领域应用广泛,例如鼻骨骨折诊断[1],早期股骨头缺血坏死诊断[2],术后辅助治疗[3]等,CT扫描在电子、材料和航空航天等领域也有着大量的应用[4]。而在CT系统成像中,参数标定和图像重建是主要的问题[5-8]。

本文主要讨论一种典型的二维CT系统,平行的X射线垂直入射于具有512个等距单元的探测器,探测器单元视作等距排列的接收点；X射线的发射器和探测器相对位置固定不变,整个发射-接收系统绕某固定的旋转中心逆时针旋转180次,以测量射线能量,并经过增益等处理后得到180组接收信息。

CT系统安装时往往存在误差,因此需要借助于已知结构的样品(称为模板)标定CT系统的参数,并据此对未知结构的样品进行成像。要求依据接收信息,确定CT系统旋转中心在正方形托盘中的位置、探测器单元之间的距离以及该CT系统使用的X射线的180个方向；在标定之后,再依据得到的标定参数,确定两种未知介质在正方形托盘中的位置、几何形状和吸收率等信息,并给出10个具体位置的吸收率。

1 基于接收信息的参数标定模型

要实现对CT系统参数标定,就是要对旋转角度、探测器间距和旋转中心的标定。

1.1 旋转角度的标定模型

对于旋转角度的标定,模板在探测器上的投影长度与旋转中心无关。从接收信息中,提取出不同角度时模板的实际投影长度,并由几何关系得到模拟投影长度,若实际与模拟的投影长度在某个角度区间相似程度较高,则认为该角度区间即为旋转角度区间。基于此,建立优化模型,将初始旋转角度和旋转间隔角度作为决策变量,将实际与模拟的投影长度间的差异大小作为优化目标,得到投影长度相似度最高的初始角度和间隔角度,从而标定旋转角度。

根据参考文献[9],可以得到X射线透射过介质时的规律为:

式中,A和A0分别为透射和入射的X射线强度,l为材料厚度,r为吸收系数[9]。我们认为该吸收系数的定义与该问题中的 “吸收率”为等价概念。

对于具有不同吸收系数的非均匀物体,可将式(1)推广为:

式中,L为X射线穿过物体的路径,r(x)表示L上某点x处的吸收率。对式(2)变换后,可以转换为:

式中,g为X射线的吸收系数r(x)在某一方向上的积分值,即为X射线成像得到的数值。由于该问题中,接收信息为探测介质吸收衰减后的射线能量在经过增益处理后得到的,故认为探测器的接收信息为:

式中,G为接收信息,c为其增益常数,下文验证了该定义的合理性。

假设有一束平行光,从某个θ角度对模板进行照射,可以得到模板的模拟投影长度Sm,若改变入射角度则可以得到模板投影长度随角度的变化曲线。给定初始角度,对入射方向连续逆时针旋转360°,可以得到模板的投影长度变化曲线Sm(θ),θ∈[0°,360°],进而得到所有入射角度下的模拟模板投影长度。

若采用X光照射模板,根据式(2),若接收信息为0,则说明X射线没有透过介质,从而可以提取出类似于光线投射时的模板投影长度,但是由于未知探测器单元的间隔,故用接收信息非0的单元数量表征投影长度。对于该问题,可以得到180个角度下的接收信息非0单元间隔数量Nm(θ0＋iβ)-1,i＝0,1, …,179, θ0为初始旋转角度,β为180次等间隔旋转的间隔角度,角度的单位均采用角度制。另外,若初始的角度相同,且认为投影接收平板足够大(板长大于该角度下模板的投影长度),则在某角度下的投影长度与旋转中心的位置无关。故可以建立目标函数:

若 θ0＋iβ 的值超过 360°则减去 360°后, 再代入模型计算。故优化目标函数可以表示为:

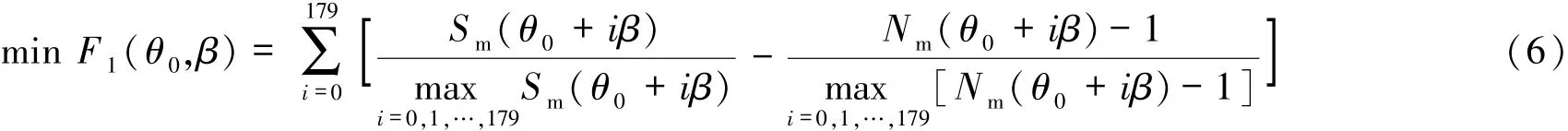
通过以上分析可知,初始旋转角度θ0和旋转间隔角度β为决策变量。对于初始旋转角度θ0,由于没有多余的信息可以约束,仅考虑旋转一周内的角度,故对θ0限定如下:

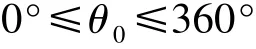
考虑到若179β＞360°时,可能会在同一角度重复投射,且间隔过大不利于对介质的检测,故对β限定如下:

基于以上分析,对于旋转角度的确定问题,建立单目标优化模型如下:

式中,Sm(θ0＋iβ) 为平行光线投射模板在 θ0＋iβ角度时的投影值,Nm(θ0＋iβ)为从X射线投射模板在θ0＋iβ角度时接收信息非0的探测器单元数量,Fi(θ0,β)为优化目标函数。通过搜索模型的最优解可以得到CT系统的180个旋转角度。

1.2 探测器间距标定模型

由1.1节模型可知,在旋转角度为θ0＋iβ时的投影长度为 Sm(θ0＋iβ),i＝0,1, …,179,而对应的接收信息非0探测器单元数量为Nm(θ0＋iβ),而探测器又是等间距并排的,故可以近似认为探测器的间距为:

式中,sd(i)为在旋转角度为θ0＋iβ时探测器单元间距的近似值,i＝0,1,…,179。

对于180个角度的接收信息,每个角度均能得到一个近似的探测器间距值sd,但由于离散化带来的误差,会导致不同入射角度时sd的值不同,但这些值都在一定范围内波动,为了减小误差,得到较为精确的探测器间距值,这里采用最小二乘法对精确值进行估计[10]。

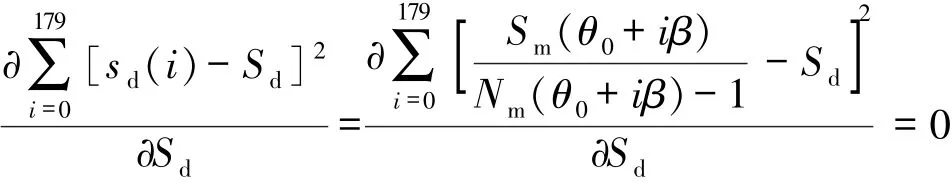
求解得到:

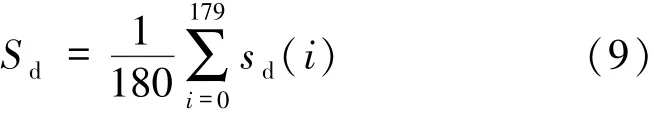
将Sd作为探测器间距值的求解结果。

1.3 旋转中心标定模型

因为探测器阵列的垂直平分线必然都交汇于旋转中心。对1.2节模型求解,可以得到探测器阵列长度,结合1.1节模型的求解结果,可得到探测器阵列的位置。根据探测器近似线段的位置和长度,可以确定线段垂直平分线。由于问题中存在180个旋转角度,每个角度均有一条近似线段的垂直平分线,任意两条垂直平分线的交点pi均可以作为旋转中心的近似位置,故存在C＝161 10个交点,即i＝1,2,…,161 00。

以托盘几何中心为原点建立如图1所示坐标系,x轴和y轴分别与托盘上边缘和左边缘平行,故近似的旋转中心可以表示为pi＝(xi,yi),i＝1,2,…,161 00。与1.2节模型类似,仍采用相似的最小二乘法对旋转中心的准确位置进行估计[3],假设旋转中心的准确位置为P＝(X,Y)。

求解得到:

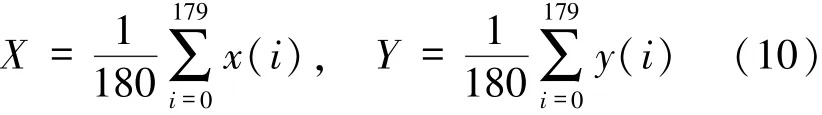
将P＝(X,Y)作为旋转中心位置的求解结果。

图1 旋转中心坐标系示意图

2 未知介质的确定模型

对于介质吸收率的确定:先用傅立叶变换将问题转换到频域上进行讨论[11],通过寻找接收信息和吸收率在频域上的关系,用频域下的接收信息反演出频域下的吸收率,从而由傅立叶逆变换反演出吸收率的结果。

对于介质形状和位置的确定:若某处存在介质,则该处吸收率必为正值,故根据吸收率是否为0判断该处是否存在介质。在已经求出吸收率的情况下,依据吸收率的大小和分布实现对介质形状和位置的重建。

对于任意介质,以介质上某一点为原点可以建立如图2所示坐标系。

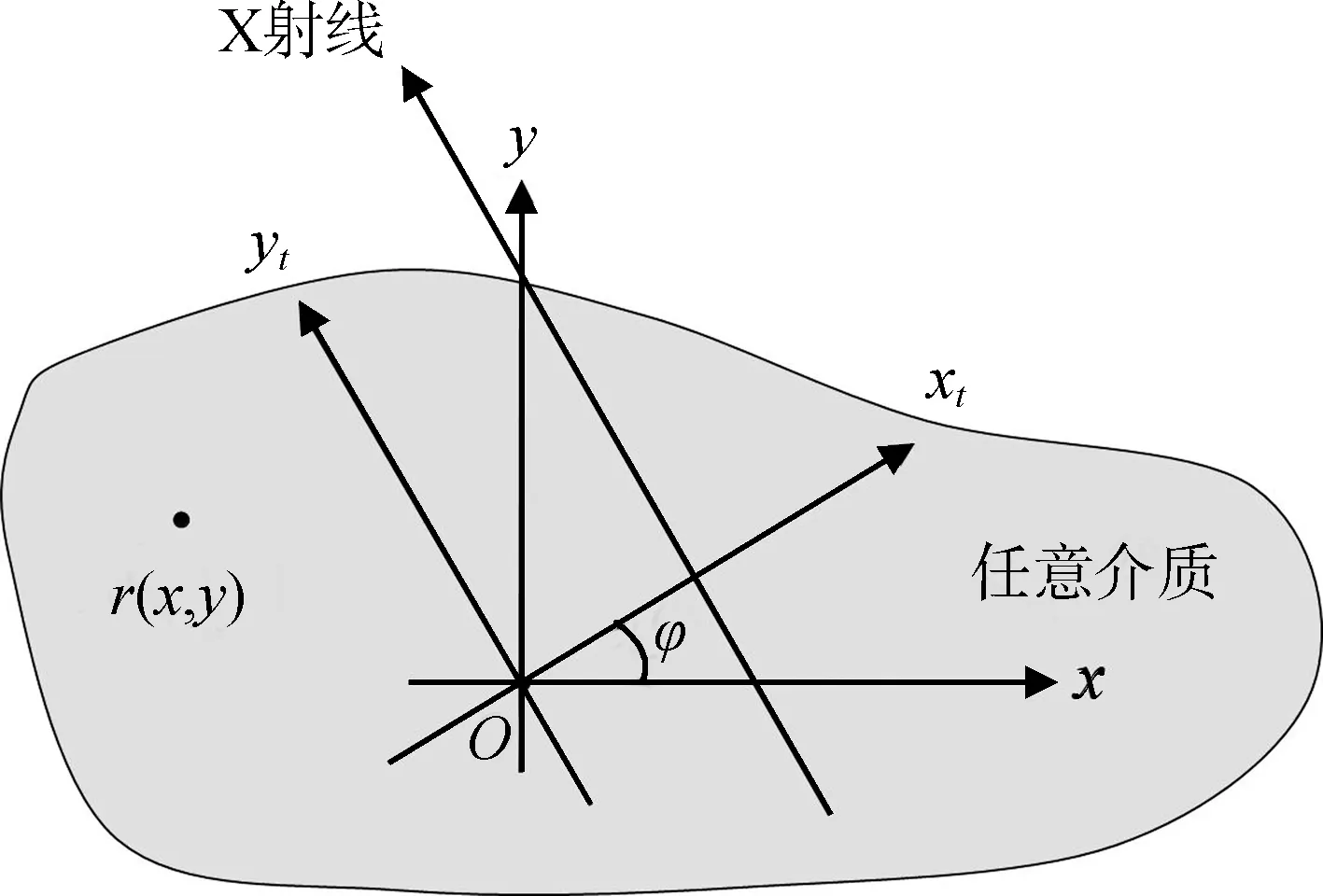
图2 确定介质吸收率模型的坐标系示意图

图2中O为坐标原点,坐标系xOy为介质坐标系,x轴和y轴分别与托盘下边沿和左边沿平行,坐标系xtOyt为投射坐标系,yt轴方向与X射线入射方向一致。要确定介质的吸收率就是要确定介质坐标系下,任意位置(x,y)处的吸收率r(x,y)。

现已知180个角度下的接收信息G,即吸收率沿180个不同角度,对于每个角度下512个探测器不同路径的积分值,要直接根据该积分值反演出吸收率是困难的。故根据参考文献[11],可以通过傅立叶变换和卷积反投影法间接得到吸收率r(x,y)的值。首先,根据Lambert-bees定理[11]得到:

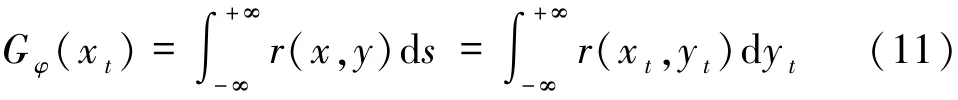
式中,Gφ(xt)是在X射线照射角度为φ的情况下,在其方向下的接收信息。对r(x,y)做二维傅立叶变换:

式中,F(u,v)为r(x,y)经过傅立叶变换后在频域的结果,u和v分别为对应的频域坐标。再对Gφ(xt)做一维傅立叶变换:

式中,ρ为频域极坐标系下的极轴,根据中心切片定理[9]:

进而可以通过对其二维傅立叶变换进行逆变换得到r(x,y)为:

式中,Φ为频域极坐标系下的极角,将式(12)改写为卷积形式:

根据Paley-Wiener定理[12],ei2πρxt是 不可积的,但只要介质的吸收率无大范围剧烈变化,则可以保证其吸收率的傅立叶变换中高频分量幅度不大,所以在实际构造卷积函数时,可以通过对卷积核H(ρ)＝｜ρ｜进行限定。根据参考文献[9]可采用如下限定:

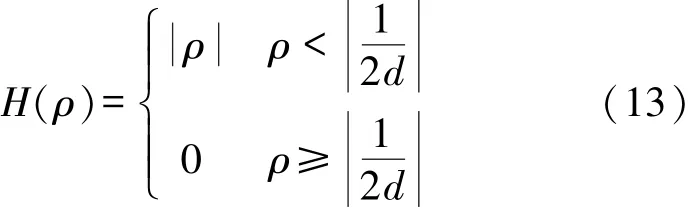
式中,d为采样间隔。

3 模型运用

3.1 参数标定结果

将所给的模板在托盘中的位置等参数代入模型中,对模型求解得到模板标定的结果如表1所示。

表1 模板标定结果汇总表

从表1中可以看出,探测器的初始旋转角度为29.666 7°,间隔为1.000 0°,则180个角度范围为29.666 7°～208.666 7°；探测器单元之间的间隔为0.276 7 mm,则512个单元组成的阵列长度为0.1414 m；在如图2所示的坐标系中,系统的旋转中心为(-9.209 4,6.115 6)mm,即旋转中心距正方形托盘的左边沿40.790 6 mm,距正方形托盘的下边沿56.115 6 mm。

3.2 介质确定结果

根据上文的模型,并用MATLAB进行求解,得到两个未知介质,即介质1和介质2的吸收率、形状和位置。

图3(a)和图3(b)分别为依据某位置介质1吸收率数据,求得的介质1的形状图像和几何参数标注图像,像素为256×256,各个位置吸收率的范围为0.0～1.4,吸收率为0的部分为无介质部分。由图3可以看出介质形状大致为椭圆,中间有两个空洞的椭圆,有两个吸收率较高的椭圆,且二者存在重叠,重叠部分的吸收率最高,以及一个吸收率不同的小圆。图3(a)中存在部分斜线,这是由于模型固有缺陷导致的伪迹；从图3(b)中可以看出,椭圆大致位于托盘中心位置,椭圆介质距托盘下边沿约10.546 9 mm,距右边沿约26.562 6 mm。

根据所给数据,对需具体求解吸收率的10个位置进行编号,如图4所示。

图3 介质1的求解结果图

图4 10个具体位置的编号示意图

通过对这10个位置的吸收率求解,可以得到结果如表2所示。

表2 介质1在10个具体位置吸收率的结果

从表2中数据可以看出,位置1、3、8、9和10处的吸收率为0,说明这些位置不存在介质。

依据某位置介质1的吸收率数据,求得的介质2的形状图像和几何参数标注图像,像素为256×256,各个位置吸收率的范围为0.0～8.0,吸收率为0的部分为无介质部分,如图5(a)和图5(b)所示。从图5(a)可以看出介质形状很不规则,为存在很多空洞的网状图形,长为94.921 9 mm,宽为86.328 2 mm。从图5(b)中可以看出,图形大致位于托盘中心位置,椭圆介质距托盘下边沿5.468 8 mm,距右边沿4.687 5 mm。

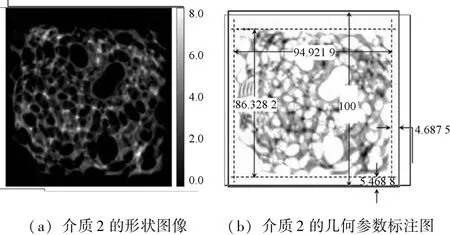
图5 介质2的求解结果图

采用与图4中一致的编号顺序,对10个具体位置的吸收率求解,得到结果如表3所示。

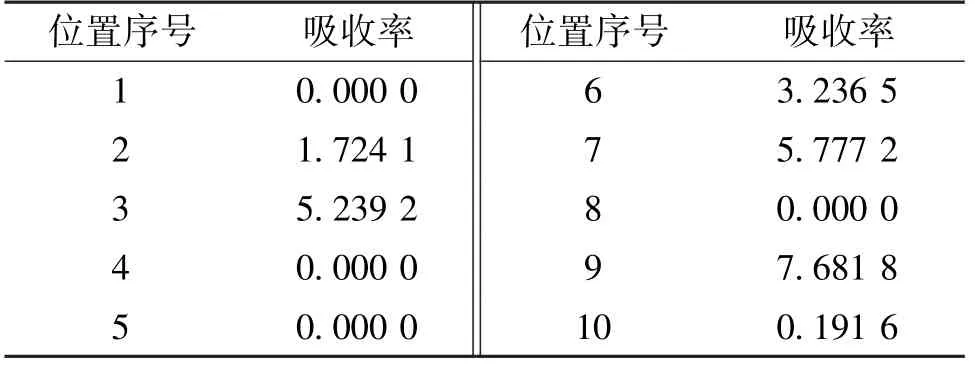
表3 介质2在10个具体位置吸收率的结果

从表3中数据可以看出,位置1、4、5和8处的吸收率为0,说明这些位置不存在介质。

4 结束语

本文针对CT系统的参数标定和未知样品的成像问题,基于模板的接收信息,建立优化模型解决了参数标定问题；采用傅立叶变换和卷积反投影法建立了介质吸收率重建模型,并根据接收信息求解出了未知介质的吸收率、形状和位置,求解效果较好。但是本文模型在物体对X射线的吸收率变化剧烈时会产生误差,需进一步改进。