CT系统参数标定及成像
耿瑞旭,吴迪远,杨广绪,程光辉
(1.电子科技大学 信息与通信工程学院,四川 成都 611731;2.电子科技大学 数学科学学院,四川 成都 611731)
CT系统可利用样品对射线能量的吸收特性对生物组织和工程材料进行断层成像[1]。本文对于一个CT系统,借助于已知结构的样品标定CT系统的参数,并据此对未知结构样品进行成像。
本文在建立了非线性规划模型,Radon反变换复原模型和切线区域验证模型后对CT系统进行标定和成像;并利用具体的模板信息和数据吸收信息对CT系统的参数进行了具体的标定,确定了CT系统旋转中心在正方形托盘中的位置、探测器单元之间的距离以及该CT系统使用的X射线的180个方向。在标定完成后,利用上述系统对未知介质的接收信息,确定该未知介质在托盘中的位置、几何形状和吸收率等信息。
1 分析与模型假设
系统三个参数的求解可以分为两个部分进行:首先求解探测器单元之间的距离及系统使用的X射线的180个方向;其次利用得到的方向变化规律和距离数值求解旋转中心。
为了利用接收器信息对轮廓规则的外形介质进行复原,可将信息复原分为三部分。
1)未知介质的位置,每次旋转时的两条切线都会得到一个可行域,对180次可行域求交集,可以得到未知介质的位置。
2)未知介质的形状,对接收信息进行反Radon变换,即可得到未知介质的形状,并可验证得到的介质形状未发生畸变,仅发生了缩放。之后,根据比例关系,得到在正方形板上实际的介质形状,并将其所在位置与第一步中得到的位置结果进行对比,从而验证形状和位置的正确性。
3)根据Radon逆变换求出介质每一点的衰减系数,再根据标定模板,求出衰减系数与吸收度的线性关系,从而进行求解,即可得到未知介质的位置、形状和吸收度。
本文假定:
1)重建CT图像时旋转中心始终不发生偏移;
2)根据CT成像原理[2-3],Radon反变换得到的衰减系数与吸收强度成比例关系;
3)标定模型的两部分分别为椭圆和圆。
2 参数标定模型的分析与建立
2.1 确定单元距离与射线方向的非线性优化模型
参数标定过程示意图如图1所示。
在此坐标系中,添加了第i次旋转时平行入射的X射线,以及椭圆吸收介质E,圆形吸收介质C,记射线l为X射线中与坐标原点距离向量最大的射线(以向上为正方向);β(i)为X射线方向与坐标系x轴正方向的夹角;s(i)表示第i次旋转时坐标原点到512个接收单元对应的射线的最大距离;d表示接收器相邻接收单元的距离。对于图1中第i次旋转时的示意图,设其中X射线的方程为:

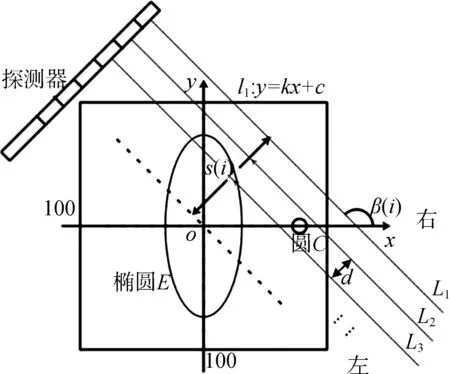
图1 标定模型探测器与射线簇示意图
首先求解X射线在椭圆中的弦长。椭圆E的方程为:

由于椭圆长轴a和短轴b的取值分别为15和40,故可得到第i次旋转时从左到右的第j条X射线穿过的椭圆形材料长度为:
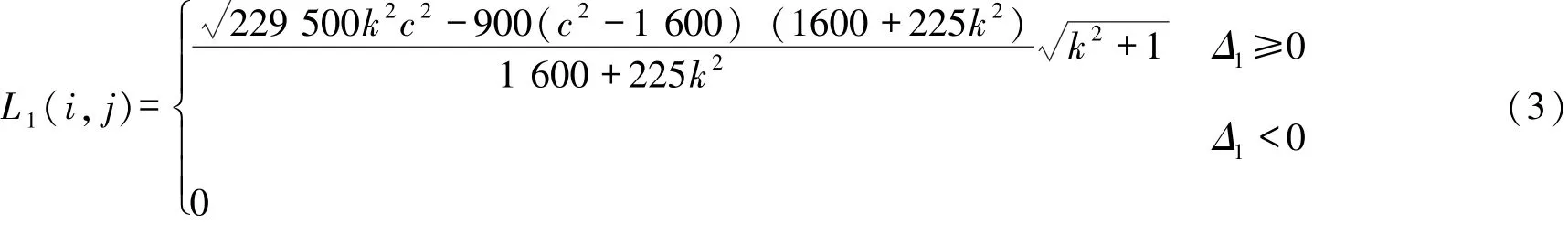
式中,
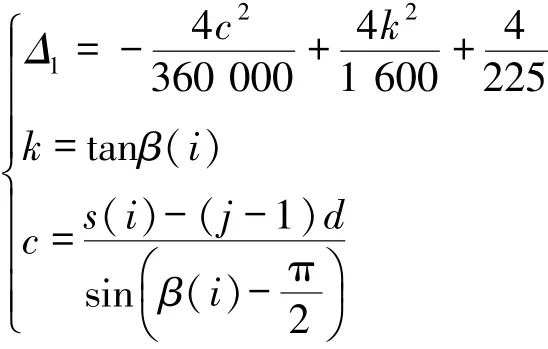
之后,求解X射线在圆中的弦长。圆C的方程为:

将X射线的方程代入式(4),可得:

式中,

最后,构造目标函数。CT系统标定时的介质对X射线的吸收是均匀的,故探测器每一个接收单元接收到的信息应与该单元接收到的信号所穿过的介质长度成正比,即:

式中:w0(i,j)为实际中给出的第i次旋转时第j个探测器的接收信息,是已知的;K为比例系数,L(i,j)为计算得到的第i次旋转时第j个探测器穿过的介质长度,即L(i,j)=L1(i,j)+L2(i,j)。为了消除接收到的信息与穿过的介质长度之间的比例关系K,本文使用了比值法,即:
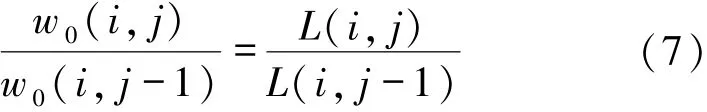
式中,等号左边为实际值,等号右边为由D(i,j)和β(i)两个决策变量构成的计算值。根据式(7),利用最小二乘原理可构造出非线性规划模型的优化函数。即:

式中:i为旋转的次数,对每一个i,均可求出一组最优的β(i)、s(i)和d;β(i)为第i次旋转时射线与x轴正方向的夹角;s(i)为第i次旋转时坐标原点到512个接收单元的最大距离;d为探测器上相邻两个等距单元的距离,应为与i无关的常量。
综上所述,本文给出非线性优化目标的优化函数如式(8)所示。
式中,
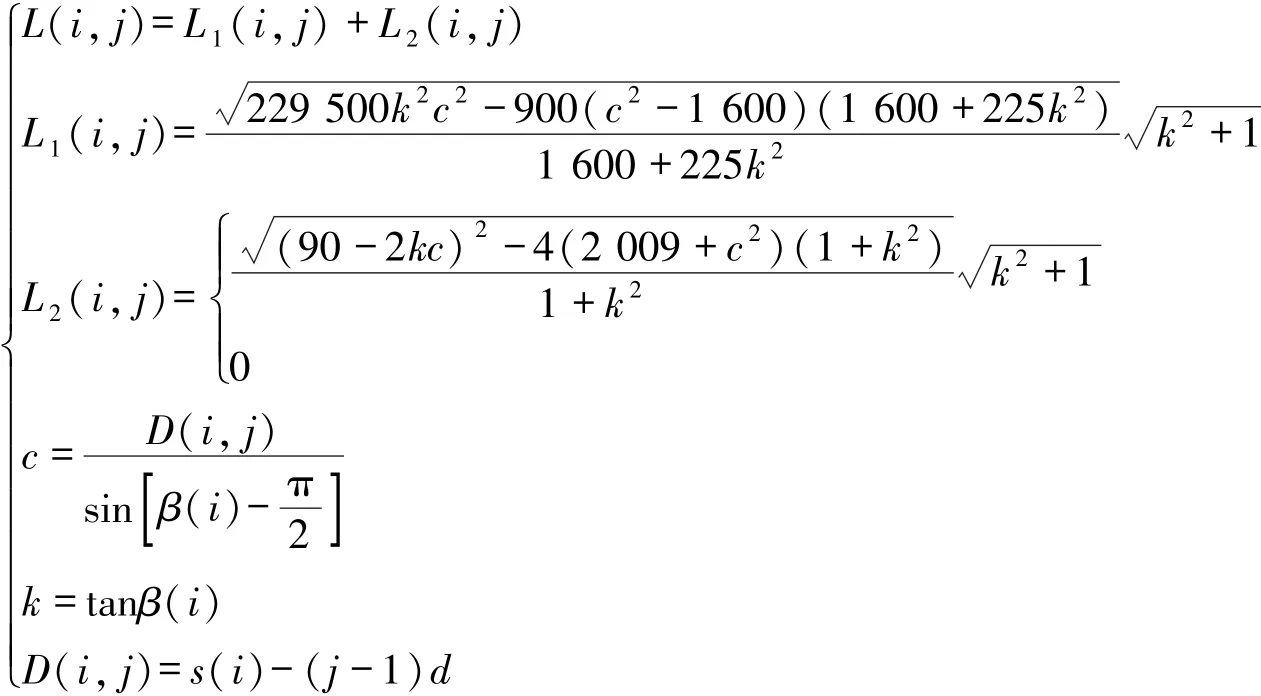
决策变量为β(i)、s(i)和d。
考虑到i有180个取值,故最后应得到180组优化结果,每组结果包含3个决策变量的最优值。
2.2 确定旋转中心位置的非线性规划模型
在图1所示的坐标系(坐标系1)中,设旋转中心点坐标为P(xo,yo),则在题目和附件给出的默认坐标系中,其坐标为P1(xo+50,yo+50)。计算时统一在坐标系1中进行计算,即以P(xo,yo)为坐标。
根据2.1节的求解结果和点到直线的距离公式,可得到第i次旋转时,旋转中心点P(xo,yo)到第一条射线的距离为:

式中:k(i)为第i次旋转时X射线的斜率,即k(i)=tan[β(i)];c1为第一条射线的截距; (xo,yo)为旋转中心点P的坐标。
由此,即可求得每次旋转时旋转中心点P(xo,yo)到第一条射线的距离r(i)。而优化目标便是使这180个距离值尽可能保持恒定,即方差尽可能小。因此,根据方差的定义,可以得到非线性规划模型的目标函数为:

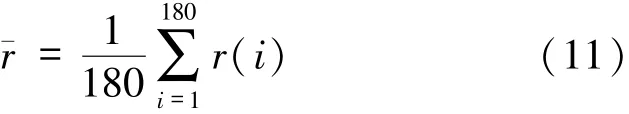
对于约束条件,主要是对(xo,yo)的坐标约束,即旋转中心应在正方形托盘中,故有如下约束:
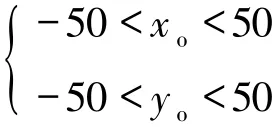
综上所述,该非线性规划模型为:
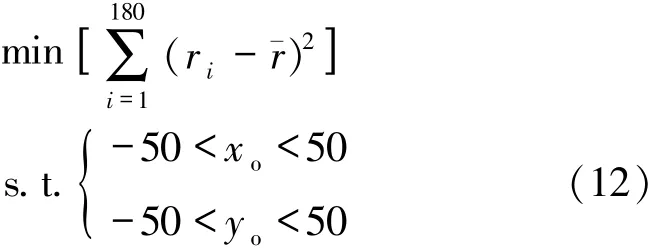
其中,旋转中心点坐标(xo,yo)为决策变量。优化目标中,r(i)的计算公式为:
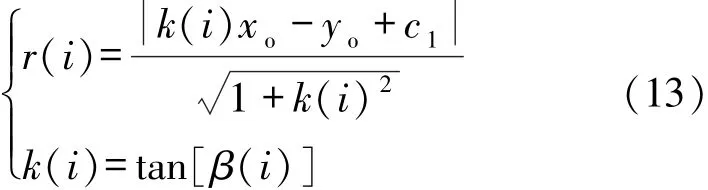
3 成像模型的分析与建立
3.1 基于切线交集的介质轮廓与未知复原模型
首先,设第i次旋转的X射线簇的斜率为ki,与待复原物质相切的两条切线的截距从大到小分别为ci,1和ci,2,则对于第i次旋转,其可行域的约束为:
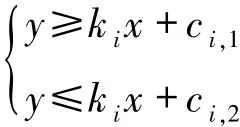
因此,对于全部180次旋转,可得如下可行域的交集表示形式,这种通过求切线所围区域的交集求出几何图形位置与轮廓的方法也可看作是一种线性规划,即:
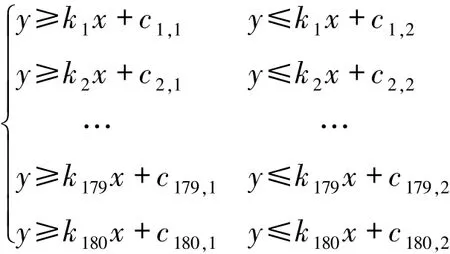
做出上述180组不等式的几何图形,即为180组切线围成的图形,也就得到了未知介质图形的轮廓与位置。
3.2 基于Radon逆变换的未知介质几何形状复原模型
Radon及其逆变换是对物体的平行束投影及其复原的数学描述。一个N维函数的Radon变换是(N-1)维超平面上的积分值,相应地,Radon逆变换就是指根据这些积分值反求得到原始被积函数[4]。在本题中,仅从二维对物体进行投影,故N=2,即函数f(x,y)为二维空间上的函数[5],其沿着任意投影射线防线的线积分就为其Radon变换。Radon变换表示为[6-7]:

Radon逆变换的公式为[8]:
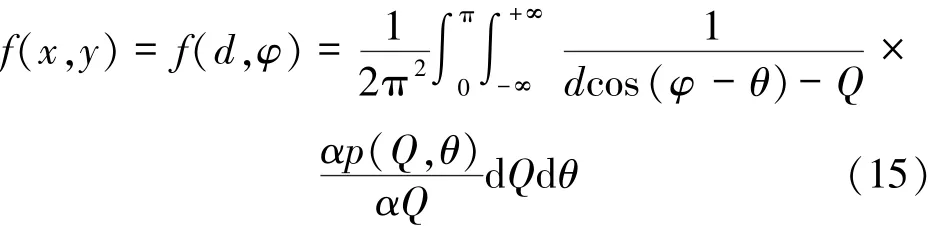
用lQ,θ表示投影射线[3],其方程为:

式中,θ代表投影射线的法线和x轴正向之间的夹角,Q代表投影射线与坐标原点之间的距离。
由此,通过对接受信息进行Radon逆变换复原原始图像是可行的。在MATLAB中,Radon逆变换的函数为iradon。
4 模型的求解
4.1 单元距离与射线方向的求解
求解该非线性约束模型的步骤如下:
1)求出由初始输入值构成的初始输入x0;
2)将x0作为初始迭代点,由fminseach函数求出极值x;
3)令x0=x,重复步骤2);
4)迭代180次后求解完成。
其中,fminsearch是MATLAB中所带的函数[9-10],但使用之前需首先求出一个合适的初始迭代点[11]。初值估计主要对第一次旋转时的角度、探测器相邻单元之间的距离和第一次旋转时第一条射线距坐标原点的距离。
首先,利用标定给出的第一次旋转时的数据。对该列数据进行绘图,如图2(a)所示;对数据表格进行二值绘图,如图2(b)所示。
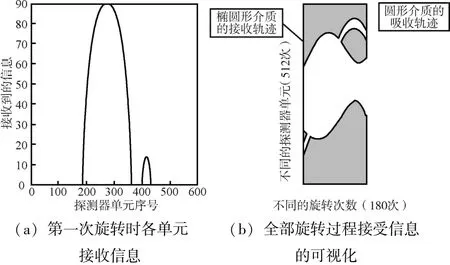
图2 初始时刻接收的信息分布图和接收信息的可视化
通过对数据进行分析,圆形介质的高度为28,即圆形介质约8 mm的直径占用了接收器大约28个单元,进而得到d的取值。最终,考虑到旋转为逆时针方向及拟合后的效果,将β(1)、d和s(1)作为初始值,代入MATLAB中fminsearch函数进行求解,可得:

4.2 旋转中心点的求解
对有约束非线性规划模型,使用MATLAB优化工具箱中的fmincon函数进行求解[1]。该模型的求解复杂度较低,故不需要对初始迭代值进行较准确的估计。根据系统的旋转中心常常与其几何中心接近的生活经验,在实际求解时,设置坐标系1中的原点(0,0)作为初始迭代点。模型的求解步骤如下:
1)将初始值(0,0)作为初始迭代点;
2)由MATLAB优化工具箱中的fmincon函数求出极值(x,y);
3)将极值(x,y)作为新的迭代点,重复步骤2);
4)求解成功后退出程序。
5 计算结果
5.1 参数标定计算结果
对探测器单元间距离和射线方向的求解结果如表1所示。
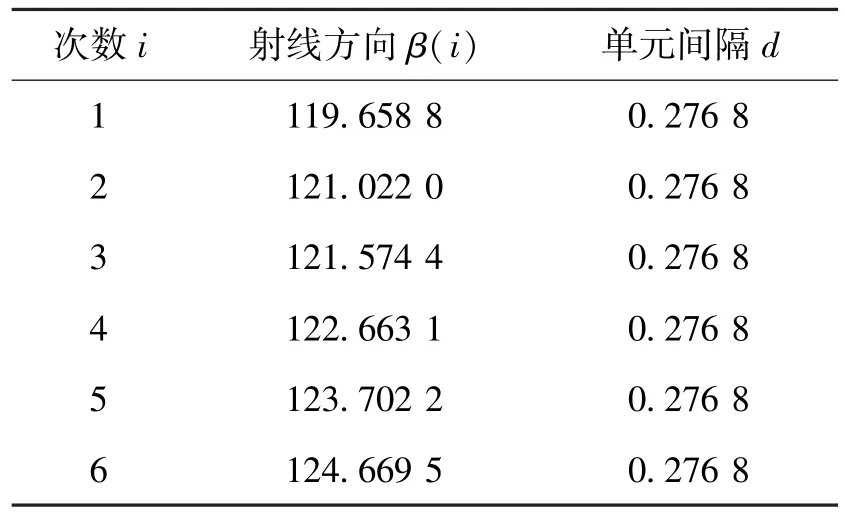
表1 CT系统参数标定结果
按照4.2节中所述的方法进行求解,可得到旋转中心P在图1所示坐标系中的位置坐标是P(-9.272 8,6.288 6)。如图3所示,给出了180个方向中的四个方向,即第一次旋转时的方向(与x轴正方向夹角),第60次旋转的方向(与x轴正方向夹角),第120次旋转的方向(与x轴正方向夹角),第180次旋转的方向(与x轴正方向夹角)。

图3 四次旋转过程示意图
5.2 未知介质复原结果
对于已有的反投影数据,可以通过切线可行域交集模型求得待测介质的位置,并通过反Radon变换得到未知介质的真实形状。

图4 图像复原结果
如图4所示,图(a)为Radon逆变换得到的直接结果;图(b)为进行按比例缩放和位置验证后的最终结果。图中心部分的大椭圆即为物体外轮廓,其中下部有两个孔洞,上部有两个椭圆形物体。由图4可知,通过Radon逆变换得到的复原结果的位置与通过取切线交集区域得到的位置几乎完全吻合。
6 结束语
本文针对CT系统参数标定的问题建立了无约束非线性规划模型,并用直接搜索法对模型进行了求解,从而得到了较为精确的CT系统参数估计模型。针对CT系统的图像重建问题,分别利用Radon反变换和切线可行域取交集法得到图像的形状和外部轮廓。

