连续时间信号自变量代换复合支

李春福，陈华伟，金燕华

(电子科技大学 航空航天学院,四川 成都 611731)

信息技术的迅猛发展与日益广泛的应用,已成为当代科学技术发展的重要特征。有关信息的获取、传输、处理、重现的基本理论和分析方法,对电子工程技术人员来说,已成为不可缺少的必备知识。对于电子信息类专业的本科、高职高专学生来说,信号与系统是重要专业基础课、核心基础课、必修课[1-12]。它以高等数学、工程数学和电路分析为基础,在课程体系结构中起着承前启后的作用,课程的教学目的是让学生掌握信号与系统的基本理论、基本原理和方法,并为进一步学习通信、控制、信息处理等课程奠定理论和实验基础,是学生合理知识结构中的重要组成部分,在发展智力、培养分析问题和解决问题的能力,以及提高综合素质等方面,都起着极为重要的作用。

广义地说,线性连续时间信号变量代换应该分为线性自变量代换和线性因变量代换两类。设a,b为任意实数,其中a≠0,那么,称f(t)与af(t)＋b之间的变量代换为线性因变量代换；称f(t)与f(at＋b)之间的变量代换为线性自变量代换[2-5]。在信号与系统课程中线性自变量代换简称为自变量代换。连续时间信号自变量代换是重要的时域知识点,是学习时域分析的一项基本训练,也是理解和应用卷积积分的重要方法[1-10]。

连续时间信号自变量代换主要包括时间平移(已知 f(t)画 f(tt0)(t0＞0时,t-t0右移,t＋t0左移))、时间反折 (已知f(t)画f(-t))、时间尺度[已知f(t)画 f(at)(0＜a＜1时,扩展；a＞1时,压缩)]3种独立出现的情形,以及这3种取任意2种或者全取3种的情形,因而共有7种情形。对于时间平移、时间尺度、时间反折单独出现的情形,可以通过简单的判断直接标注所要代换的连续时间信号波形,连续时间信号自变量代换的时间平移、时间反折、时间尺度三种独立出现的情形如图1所示。

而对于2种或3种自变量代换一起出现的情形,可以采用逐一先后实现其中各种代换的方法。如对于3种代换都有的情形,会有时间平移—时间反折—时间尺度、时间平移—时间尺度—时间反折、时间尺度—时间平移—时间反折、时间尺度—时间反折—时间平移、时间反折—时间平移—时间尺度以及时间反折—时间尺度—时间平移六种顺序实现思路,当然每一个顺序实现思路都必须注意自变量代换的相应特点[1-5]。文献[2-4]写明了,对于连续时间信号自变量代换正支 (已知x(t)画x(at＋b)),当时间平移、反折、尺度一起出现两种或三种的情形可以按照6种顺序中的任何一种完成代换转形绘制。文献[2]进一步报道,对于连续时间信号自变量代换逆支(已知x(at＋b)画x(t)),当时间平移、反折、尺度一起出现两种或三种的情形也可以按照6种顺序中的任何一种完成代换转形绘制。

图1 时间平移、反折、尺度

本文提出,对于连续时间信号自变量代换复合支(已知x(at＋b)画x(ct＋d),即已知代换波形画代换波形),当时间平移、反折、尺度一起出现两种或三种的情形,依然可以按照6种顺序中的任何一种完成代换转形绘制。对连续时间信号自变量代换复合支,选择文献[1]中给出的顺序实现解题思路时间平移—时间反折—时间尺度 (是6种顺序中优先的一种,注意到时间平移是线性时不变系统,时间反折是只涉及信号波形颠倒的线性时变系统,时间尺度是涉及信号波形压缩扩展的线性时变系统),确定了根据自变量代换前向变化关系按照时间平移—时间反折—时间尺度优先顺序绘制自变量代换复合支的相应理论,提供的例题阐述了应用,利用MATLAB做了语音实验。

1 绘制自变量代换复合支相应理论

对于确定的参数a,b,c,d,x(at＋b)和x(ct＋d)是一一对应的,考虑各种a,b,c,d参数取值,已知x(at＋b)画x(ct＋d),首先确定自变量代换前向变化关系为将x(at＋b)中的自变量t前向变化为, 即式 中,为平移量,sign为平移符号量,反折符号量尺度量。显然通过完成此前向变化关系就可以完成从x(at＋b)到x(ct＋d)的代换转形。进而根据文献[1]中的优先顺序 (时间平移—时间反折—时间尺度)可以简单地完成代换转形绘制,其中优先顺序具体如下:

2 例题

2.1 已知x(t)波形画x(at＋b)

例1 如图2所示,已知x(t)＝[-U(t＋2)＋(t＋2)U(t＋2)] ＋[U(t＋1)-(t＋1)U(t＋1)] ＋[U(t)]＋[-U(t-1)＋(t-1)U(t-1)]＋[(t-2)U(t-2)]画x(-t/2＋4)。

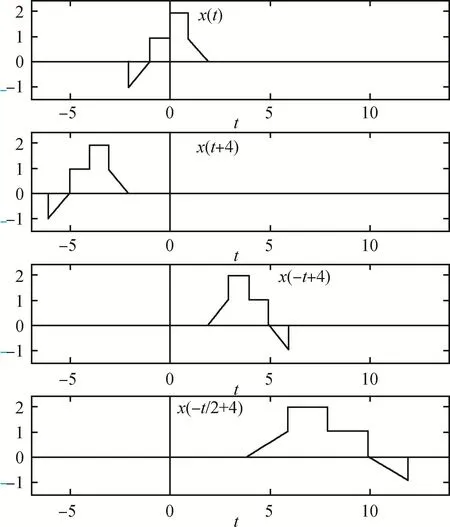
图2 已知x(t)波形画x(at＋b)

首先,确定自变量代换前向变化关系为t→-t/2＋4,其中平移量为4,平移符号量为sign(4)＝′-′,反折符号量为 sign(-1/2)＝′-′,尺度量为然后,采用优先顺序完成代换转形绘制:

1)时间平移:

平移量4,平移符号量′-′,向左平移4。

2)时间反折:

反折符号量′-′,有反折。

2.2 已知x(at＋b)波形画x(t)

例2 如图3所示,已知x(-t/2＋4)＝[-U(-t/2＋6)＋(-t/2＋6)U(-t/2＋6)]＋[U(-t/2＋5)-(-t/2＋5)U(-t/2＋5)]＋[U(-t/2＋4)]＋[-U(-t/2＋3)-(-t/2＋3)U(-t/2＋3)]＋[(-t/2＋2)U(-t/2＋2)]画x(t)。

图3 已知x(at＋b)波形画x(t)

首先,确定自变量代换前向变化关系为t→-2(t-4)＝-2t＋8,其中平移量为8,平移符号量为 sign(8)＝′-′, 反折符号量为 sign(-2)＝′-′,尺度量为｜-2｜＝2。然后,采用优先顺序完成代换转形绘制:

1)时间平移:

平移量8,平移符号量′-′,向左平移8。

2)时间反折:

反折符号量′-′,有反折。

3)时间尺度:

尺度量2＞1,压缩2倍。

2.3 已知x(at＋b)波形画x(ct＋d)

例3 如图4所示,已知x(-t/2＋4)画x(2t/3＋1)。

首先,确定自变量代换前向变化关系为t→-2(2t/3＋1-4)＝-(4/3)t＋6,其中平移量为6,平移符号量为sign(6)＝′-′,符号量为sign(-4/3)＝′-′,尺度量为然后,采用优先顺序完成代换转形绘制。

1)时间平移:

平移量6,平移符号量′-′,向左平移6。

2)时间反折:

反折符号量′-′,有反折。

3)时间尺度:

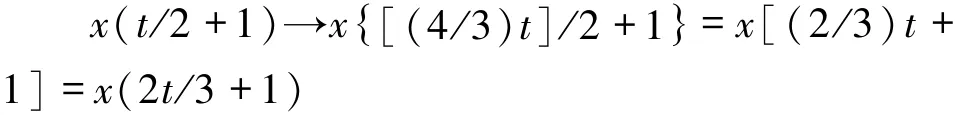
尺度量4/3＞1,压缩4/3倍。

图4 已知x(at＋b)波形画x(ct＋d)

3 MATLAB语音实验

利用MATLAB,对记录的语音信号进行了时间平移(右移和左移)、时间反折、时间尺度(压缩和扩展)的实验演示,让同学们直接看到听到声音信号的自变量代换效果。

首先,采用Windows自带录音机完成语音信号的录制,一般录音信号的格式是(∗.wma),进行格式转换后成为(∗.wav)格式。然后,就可以利用MATLAB的wavread函数对记录的语音信号进行输入,输入后产生得到两路语音信号、采样频率和量化比特值；利用MATLAB的sound函数可以对代换后的语音信号进行输出。

3.1 语音信号时间平移

语音信号的时间平移如图5所示,同时利用MATLAB语音播放函数可以听到在扬声器里发出相应的声音变化。其中,x(t)为语音波形,t0＞0,x(t-t0)为向右平移后的语音波形,听音效果表现为时间延迟加大；x(t＋t0)为向左平移波形,听音效果表现为时间延迟减小。

图5 语音信号时间平移

3.2 语音信号时间反折

语音信号的时间反折如图6所示,同时利用MATLAB语音播放函数听到感受在扬声器里发出相应的声音变化。其中,x(t)为语音波形,x(-t)为时间反折语音波形,听音效果表现为声音倒着出来。

图6 语音信号时间反折

3.3 语音信号时间尺度

语音信号的时间尺度如图7所示,同时利用MATLAB语音播放函数可以感觉到在扬声器里发出相应的声音变化。其中,x(t)为语音波形,x(2t)为时间压缩2倍的语音波形,听音效果表现为语音加速,声调提高。x[(1/2)t]为时间扩展2倍的语音波形,听音效果表现为语音速度减慢,声调降低。

图7 语音信号与时间尺度

4 结束语

本文明晰了连续时间信号自变量代换复合支,给出了根据自变量代换前向变化关系按照时间平移—时间反折—时间尺度的优先顺序绘制自变量代换复合支的相应理论,提供的例题阐述了应用,利用MATLAB进行了语音信号实验。

向电子科技大学秦开宇教授、张鹰教授和加州大学-圣克鲁斯分校的同事表示谢意。