冲泻区形态动力学耦合模型研究Ⅰ:分段输沙率公式建立
邓 斌 ,蒋昌波 ,杨树清 ,陈 杰
(1.长沙理工大学 水利工程学院,湖南 长沙 410114;2.水沙科学与水灾害防治湖南省重点实验室,湖南 长沙 410114;3.School of Civil,Mining and Environmental Engineering,University of Wollongong,Wollongong,Australia 2522;4.长沙理工大学 水科学与环境工程国际研究中心,湖南 长沙 410114)
1 研究背景
冲泻区(Swash zone)是沿海周期性受上爬水流覆盖和水流回落后裸露,处于水流爬高最高位置与回落最低位置之间的岸滩,也是海岸带中水动力作用最激烈和泥沙运动最活跃地带[1-2],其水动力和泥沙运动情况对海陆相互作用的强度、海滩剖面变化、海岸线演化、海岸建筑稳定性以及海岸带生物的发育繁殖等起着极其重要作用[3]。已有研究表明,岸滩中大部分的侵蚀和淤积都集中发生在冲泻区[4]。而该区域水深较浅,波浪上爬和回落时间通常较短、水流加速快,现场和实验室观测非常困难[5],对该区域的水动力特性、泥沙输运过程的研究十分欠缺,深入开展相关研究十分必要。
国内外很多学者一直致力于波浪作用下输沙模式的研究,建立了许多应用于破碎带泥沙运动的计算模式(详见文献[6-7]),但针对冲泻区复杂非线性水动力作用下的输沙模式则相对较少。冲泻区内的泥沙运动主要呈层移(Sheet flow)形式[8],部分学者基于恒定流简化冲流过程建立了应用于冲泻区的泥沙输运公式,一定程度上解释了岸滩响应关系。如:Nielsen[9]基于能量的河流泥沙输运公式,提出了可描述水流加速影响下的悬移质泥沙输运模型,并预测了冲泻区内的泥沙输移。Butt[10]认为在波浪反射较大的情况下,采用能量公式预测冲泻区内的泥沙输移不一定准确,在充分考虑冲泻区冲流紊动和床面渗透性基础上建立了冲泻区泥沙输运概念模型。类似的工作还有Masselink和Hughes[11]、Puleo等[12]、Masselink 和 Russell[13]、Sumer等[14]开展的研究。
现有研究多是借鉴单向流输沙理论中基于能量形式的公式,并通过修正希尔兹参数建立输沙率计算公式。然而,冲泻区水动力呈明显的非恒定流和往复流特性,其作用下的泥沙输运与单向流作用下的特性差异大,同时还受岸滩边坡、地下水出入渗等因素的影响,特别是由非黏性沙组成的沙质岸滩。如Barnes和Baldock[15]认为冲泻区内泥沙输运主要受内破碎区和岸滩坡度控制。Elfrink和Baldock[4]提出冲泻区为达到岸滩平衡存在泥沙输运的不对称性。Masselink等[16]认为若上爬与回落过程中的输沙率相等,相比上爬过程,相对较长的回落过程将会侵蚀更多的泥沙。此外,冲泻区特有的振荡环境下泥沙运动还受到岸滩地下水这类高阶非线性过程的影响[17]。如陆彦等[18]用水槽试验测定沙波的尺寸及运动速度与床面渗流水力梯度的关系,并结合理论分析,推导出推移质输沙率随床面渗流变化的计算公式,认为渗流的作用不应忽略,但该研究只是针对明渠恒定流的情况。这些研究工作一定程度推进了冲泻区泥沙输运的研究进展。
综上所述,尽管目前通过研究对冲泻区岸滩形态变化规律有了一定的认识,提出了一些冲泻区泥沙输运模式[19-20],但准确预测冲泻区的泥沙输运仍然是一项非常具有挑战的工作,必须更全面考虑水沙动力相互作用机制,如:紊动、床面剪切应力、床面摩阻、非恒流作用下产生的垂向流速、水流入渗/出渗、坡度等对泥沙运动的影响[17]。为此,本文在实验和前人研究基础上,拟提出非恒定流作用下考虑垂向流速、水流入渗/出渗、坡度等影响因素的冲泻区非黏性泥沙运动输沙率公式,为进一步了解沙质岸滩的侵蚀机制和后续岸滩形态动力学模型的建立奠定基础。
2 冲流过程中斜坡上床面泥沙受力分析
冲流过程中,冲泻区内冲流水深迅速从零增加到几厘米甚至十几厘米。在这种水流快速变化下,泥沙运动的响应也非常迅速。在水流上爬(Uprush)阶段,沿岸滩方向的重力分量和水流入渗力抑制了泥沙的运动;在回落(Backwash)阶段,沿岸滩方向的重力分量和水流入渗力促进了冲泻区泥沙的运动,水流出渗。因此,分析波浪作用下的岸滩泥沙运动力学机理时除考虑重力作用外,还需考虑渗流的影响。考虑泥沙的临界起动状态,对波浪上爬和回落两个阶段下床面单个泥沙颗粒主要受力进行分析,参见图1。

图1 泥沙受力分析示意图

式中:W为泥沙颗粒的有效重力;FD和FL分别为水流产生的拖曳力和上举力;f为摩擦力;k为摩擦系数;S为渗流力,其中水流上爬到岸滩上时会产生垂直于岸滩向下的入渗水流,形成水流入渗力Sin,相反,水流反转后,岸滩逐渐裸露出来,岸滩中的地下水会产生垂直岸滩向上的出渗水流,从而形成水流出渗力Sex。
在水流回落阶段,泥沙颗粒垂向和水平受力力矩平衡方程为:

由图1和式(1)~式(4)可知,在水流上爬阶段,水流入渗力使得泥沙所需的起动拖曳力增加,从
在水流上爬阶段,泥沙颗粒垂向和水平受力力矩平衡方程为:而导致颗粒不易起动;而在水流回落阶段,水流出渗力向上促使泥沙所需的起动拖曳力减小,泥沙起动更容易。Alfadhli等[21]对渗流影响下泥沙受力进行了形象的描述,认为水流入渗导致泥沙变成“铁沙”,水流出渗导致泥沙变成“塑料沙”。Butt等[22]认为在由粗沙组成的床面上,水流入渗和出渗对泥沙向岸输运的影响非常大,并指出存在一个泥沙粒径临界值,小于该临界值时入渗和出渗会导致泥沙离岸输运,大于该临界值则泥沙向岸输运。
3 考虑不同因素影响下希尔兹参数修正方法的讨论
3.1 考虑垂向流速的影响 Alfadhli等[21]认为泥沙运动不仅要考虑水平剪切流速的影响,还不能忽视垂向流速的影响,减速流会促进向上流动,向上的流速可提高颗粒的移动性,加速流会促进向下流动,向下的流速会增加颗粒的稳定性;推导出影响泥沙运动并含水平流和垂向流相关参数的方程。在考虑由主流所产生的垂向流速时,还需考虑表层水的入渗以及地下水的出渗,因此净垂向流速为Vs=Vs1+Vs2,其中Vs1为地下水的水力梯度i引起的垂向速度(也即渗流速度),Vs2为主流的非恒定性或非均匀性所引起的垂向速度。当Vs2和Vs1的方向相反时,净垂向流速Vs可能为零,籍此可解释前人实验虽观测到渗流,但为何没有影响到泥沙运动的现象(Watters和Rao[23])。考虑主流非恒定性或非均匀性所引起的垂向速度Vs2,并考虑水平和垂向的立面二维流动,基于连续性方程得到垂向流速的表达式:,其中∂u/∂x为水平流速u沿x方向的梯度,如果下游流速增加(加速流),则∂u/∂x为正值;如果水流经历减速流,则∂u/∂x为负值。因此,加速流会产生一个负(向下的)垂向流速v,减速流会产生正(向上的)垂向流速v,v值即为Vs2。Alfadhli等[21]认为由于垂向流速的存在,可能会导致观测到的临界剪切应力值大于或小于希尔兹参数的预测值,因此采用传统的希尔兹数判断泥沙的起动是不合适的。考虑垂向流速的影响,从力平衡方程出发得到垂向流速影响下的泥沙有效重度的变化关系,可得到修正后的临界剪切应力为:

式中:τ′c为考虑垂向流速的临界剪切应力;ω为泥沙沉降速度; ρs和 ρ分别为泥沙和水的密度。与原始希尔兹参数相比可得:

从式(6)分析可知,临界剪切应力的修正只是针对渗流引起的有效重度变化,并未体现到由于渗流影响床面剪切应力的改变。
3.2 考虑坡度与渗流流速共同作用 冲泻区泥沙运动不仅要考虑重力的影响,还需考虑渗流的影响。重力分量的大小与岸滩坡度有关,渗流的影响改变了边界层的厚度(即床面剪切应力发生改变),因此需从坡度和床面剪切应力两方面分析渗流对岸滩演变的影响[24]。前人研究渗流对冲泻区泥沙运动的影响时,认为冲泻区的泥沙运动可归功于以下两种方式[22,25-26]:(1)床面泥沙颗粒有效重度的增加,有利于床面的稳定;反之,会导致床面不稳定;(2)作用于床面泥沙颗粒上剪切应力的增大和减小分别对应于边界层厚度的减薄和增厚。为了解释这两种方式联合作用下的泥沙运动机理,前人根据修正希尔兹参数提出了一些经验模型,如Nielsen模型[25]、Turner和Masselink模型[26]和Liu模型[24]。对这3种模型的归纳及分析如表1所示。
对比3种希尔兹参数修正模型可知,Alfadhli模型虽考虑了主流中垂向流速和渗流流速的联合作用,但只对希尔兹参数中有效重度的变化进行了修正;Nielsen模型和Turner和Masselink模型均考虑了渗流对床面剪切应力和泥沙有效重度的影响,但均存在一定的局限性;Liu模型在Turner和Masselink模型的基础上,考虑斜坡上泥沙运动情况,增加了坡度对泥沙起动的影响,但认为渗流对泥沙有效重度的影响非常有限,模型中舍弃了渗流对泥沙有效重度的改变效应。

表1 不同希尔兹修正模型
4 冲泻区有效希尔兹参数的修正及参数确定
4.1 冲泻区有效希尔兹参数的修正 由于冲泻区水流运动的强非恒定性和非均匀性,冲泻区泥沙运动可近似看作是非恒定流下的泥沙运动,水流上爬和回落两个阶段可分为两个相互独立的过程[27],考虑不同岸滩坡度影响,结合本文第3节中所考虑净垂向流速(含渗流流速和主流产生的垂向流速)和岸滩坡度对冲泻区泥沙运动的影响,在Liu模型的基础上考虑主流产生的垂向流速和有效重度改变(即Alfadhli模型),可得到符合冲泻区水沙动力运动物理过程的瞬时希尔兹参数计算公式:

式中:γ为岸滩坡度;ϕ为泥沙的内摩擦角;Vs为主流加速或减速引起的垂向流速Vs2和渗流流速Vs1的共同作用。式(9)中当Vs1<0时,sign(Vs1)为负,对应于水流上爬阶段,反之对应于水流回落阶段,而式(10)由于同时考虑了Vs1和Vs2,使用sign(Vs1)不能反映水流离岸还是向岸运动,故式中采用u/|u|来表示水流运动方向,当u/|u|=1时表示水流上爬阶段,u/|u|=-1时表示水流回落阶段。系数b取2.0[28],fw为摩阻系数,ω为沉降速度。
4.2 参数确定 式(10)中坡度γ可直接测量得到,但还需确定Vs、fw和ω。其中Vs的计算分两部分,主流运动产生的近底垂向流速可近似为定床测量得到的近底垂向流速Vs1,渗流产生的床面渗流流速Vs2可通过测量岸滩中的孔隙水压力近似计算;fw在冲流过程中是随时间变化的,计算时近似采用定床情况下计算得到的Cf,即fw=αCf,α取值0.1~1.0[29-30];ω根据泥沙属性计算。下面将结合实验详细分析各参数的计算。
4.2.1 实验设置 实验在长沙理工大学水沙科学与水灾害防治湖南省重点实验室的PIV专用水槽中进行,水槽尺寸为20.0 m×0.4 m×0.5 m,总体误差小于1.0 mm,水槽两侧为透明玻璃。本研究在水槽内设置溃坝生成涌浪实验装置,如图2所示,在水槽左端采用两块厚2 mm的铝板封闭,其中右边铝板设置为可上下移动的闸门,与水槽两侧形成一个1.0 m长、0.4 m宽的水箱。闸门顶部采用不可拉伸的细绳连接,通过滑轮,细绳另一端配重10.0 kg,闸门的开启通过电磁开关控制配重的释放,可在0.2 s内被完全抽起,溃坝产生的波浪在下游发生卷破,并形成高强度的涌浪和随后的冲流事件。实验布置如图2所示。

图2 实验布置图
冲泻区岸滩地形分别概化为1∶10沙质斜坡、1∶35沙质斜坡以及 1∶10和 1∶35的复式沙质斜坡。斜坡起点位于x=0.0 m位置,采用实验标准筛筛好的泥沙铺成。其中,均匀沙粒径为0.456 mm的中沙,非均匀沙由粒径为0.895 mm粗沙、0.456 mm中沙和0.267 mm细沙按1∶1∶1的质量比混合而成。通过对均匀沙和非均匀沙各3次随机取样,利用激光粒度仪进行级配测试,绘制级配曲线见图3。对3次测试结果进行平均,得到均匀沙粒径为0.456 mm;非均匀沙中值粒径为0.464 mm,不均匀系数为2.87。实验工况如表2所示。

图3 泥沙粒径级配曲线

表2 实验工况
实验中采用孔隙水压力计(PPS)测量岸滩的地下水响应,从而分析渗流对岸滩演变的影响,孔隙水压力计布置见表3;并通过在岸滩上不同断面布置集沙盒(长10.0 cm×宽40.0 cm×深10.0 cm)采集上冲流和回落流过程中泥沙的沉积量,从而计算得到各断面推移质输沙率,测量的断面位置见表4。测量时,一个断面分两次单独冲流过程收集,第一次收集水流上爬产生的泥沙沉积,随后把床面泥沙均匀混合并整平,第二次收集水流上爬和回落两个阶段产生的泥沙沉积,每个断面重复3次,则每测量一个断面共重复6次冲流过程。
4.2.2 Vs的计算 在上述模型中,准确有效的测量渗流速度非常重要。本文基于实验测量得到孔隙水压力并结合渗流达西公式计算渗流速度Vs1:

上式中,假设同一垂线上的两点z1和z2的测量到压力值分别为p1和p2,则上式可变为:

表3 孔隙水压力计测量布置(单位:m)
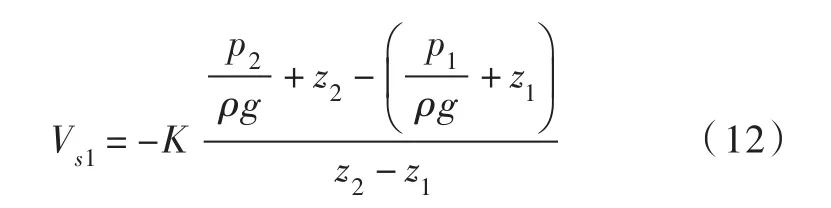
通过式(12)便可计算得到渗流速度Vs1。另外,水力传导系数K的计算采用文献[31]中的公式计算:
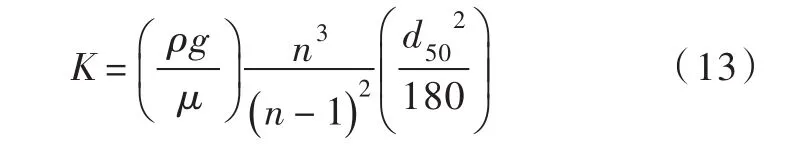
式中: ρ为水的密度;动力黏度系数μ=10-3Nsm-2;孔隙率n≈0.45;d50为泥沙中值粒径。在本文沙1和沙2下,K分别取值0.0034和0.0035 m/s。
由于泥沙不断运动,难以准确的测量到近底层流速,故Vs2采用定床下通过PIV系统测量得到的结果近似,在一定坡度γ下,通过流速分解得到垂直于岸滩的流速Vs2=wcosγ-usinγ。

表4 集沙盒布置
4.2.3 fw的计算 摩阻系数fw在整个冲流周期内是变化的[31],其值的确定非常困难[32]。Butt等[22]等认为摩阻系数的计算可采用无渗流情况下恒定流的公式估算,并假设冲泻区内水流上爬和回落为独立的准恒定流过程;Nielsen等[34]基于线性波理论,推导出床面可渗情况下的波浪摩阻系数计算公式。然而这2种计算公式得到的fw为定常数。在实际情况中,冲泻区内不同断面在不同时刻其fw均是变化的,因此采用动态摩阻系数计算更符合实际,O'Donoghue等认为动床下床面摩阻系数为定床的α倍,即:fw=αCf,Cf为光滑床面下测量得到的摩阻系数[29]。此外,水流上爬阶段和回落阶段的床面摩阻系数也并不相等,如:Masselink等[13]和Barnes等[35]通过现场观测发现床面摩阻系数系数在水流上爬阶段约为回落阶段的2倍。本研究在光滑定床实验中[36]同样发现,水流回落阶段的床面摩阻系数大约为上爬阶段床面摩阻系数的0.88倍。因此在计算中应分别考虑水流上爬和回落阶段的床面摩阻系数。本研究计算中,α取值为2。
4.2.4 ω的计算 本研究考虑非黏性沙,无黏性沙沉降速度计算采用如下公式[37]:

式中:s=ρs/ρ为泥沙相对密度;ρs为泥沙密度;ρ为水的密度;d为泥沙粒径;v为水的运动黏滞系数。
计算得到沙1和沙2的沉降流速分别为0.0677和0.0667 m/s。
5 冲泻区分段输沙率公式的建立
前人基于恒定流假设,运用动力学、流速、能量平衡等理论为依据推导的输沙率公式相对较多,然而冲泻区内的水流运动本质上属于非恒定流,涉及冲泻区内薄层水流运动中输沙公式的研究非常少。部分学者采用推移质输沙率与流速u(或流速u和水深h)的高次方成正比的关系(q(u)或者q(h,u))描述冲泻区内的泥沙输运[14,38],然而这类幂次定律公式在解释冲泻区床面演化时仍然存在许多不足[39],如输沙率采用q(u)公式可能高估了浅水区的泥沙输运,而q(h,u)类型的公式体现了泥沙输运受到水深的控制,通常仅适应于较小的水深。考虑冲泻区水沙运动实际情况,冲泻区的输沙率公式应能体现低、中冲泻区输沙强度由流速主导、高冲泻区输沙强度由水深主导的关系[40]。
在Zhu[40]的研究基础上,充分考虑冲泻区不同位置水深和流速的影响,首先假定输沙率qb=q(h,u),并分段考虑推移质输沙率为速度和水深的函数,即在x/Rx<L范围内采用Meyer-Peter Müller的输沙公式 q∝θ3/2[41],而在 L<x/Rx≤1的范围内采用 Pritchard和 Hogg输沙公式 q(h,u)[42],具体形式为:

式中:x为起始于初始岸线沿岸滩的位置;Rx为最大上爬高度相对于初始岸线的位置;x/Rx<0表示离岸位置,x/Rx=1表示最大上爬高度位置处;L代表冲泻区内水深相对于流速对输沙率起主导对应的位置。A1的确定如下,由 Meyer-Peter Müller的输沙公式[41]:

令 θcr=0,结合式(10)可把式转化为推移质输沙率为速度的指数函数的形式,则有:

对比式(15a),并代入到式(10),则可得A3为:
式(15)总体含义表示,当流速对输沙率影响起主导作用的时候,采用流速的指数公式计算;当水深对输沙率起主导作用的时候,采用水深乘流速的指数公式计算,其中A2取值为0.015 s-2m-2。该公式的特点是考虑薄层水流运动引起的泥沙运动。式(15)中尚需对参数L进行讨论,即选择合适的划分冲泻区薄层水流所对应的位置,具体由下文基于实验拟合得到。
6 实验验证
基于上文建立的分段输沙率公式,根据实验实测资料对公式进行验证。首先以Case1的x=1.5 m断面为例,各参数的计算过程结果如图4所示。
图4(a)(b)分别为实验测量得到的冲流水深和水深平均流速随时间的变化。图4(c)给出了由实验数据分解得到主流非恒定运动产生的垂向流速Vs2和基于式(12)计算得到的渗流流速Vs1。从图中可见,该断面下冲流过程中渗流流速均为负数,均值为-0.0039 m/s,表明该工况冲流过程中主要以水流入渗为主,这与实验中观测到的现象基本一致,实验中观察到的出渗水流是在冲流过程结束一段时间后才出现,即出渗并未出现在水流回落阶段,而是存在一定的滞后;由主流产生的垂向流速可见,垂向流速Vs2的平均值为-9.4×10-6m/s,仅在水流上爬初期产生了垂直岸滩向上的较大流速,其他情况下均为负数,但均接近于0 m/s,在水流回落晚期出现正负波动。叠加后的垂向流速显示,除上爬初期由Vs2主导外,其他时刻与Vs1相差不大,平均值为-0.003 88 m/s。
图4(d)(e)也分别给出了Vs1和Vs2单独作用下以及联合作用下相对希尔兹参数和推移质体积输沙率随时间的变化。分析可见,垂向流速V中Vs2的增加对θ/θ0和q产生了一定的影响,特别是水流上爬初期影响较大,水流上爬阶段产生的垂直岸滩向上的流速平衡了该时段水流入渗所产生的作用,而在其他时段由于Vs2相对Vs1太小,Vs2的作用得到了限制,Vs1的作用更为明显,特别是在水流上爬晚期至回落结束,联合作用下的q与Vs1单独作用计算得到的q基本一致。综上可见,考虑Vs1和Vs2的联合作用更为合理。
为保持与实验测量一致,对推移质输沙率q进行时间上的积分,可得该断面上的单宽输沙率。根据实验测量断面,分别按照上述计算过程对所有断面进行计算,计算中先不考虑L的取值,两种输沙公式同时计算,结果如图5所示。从图中可见,采用分别采用式(15a)和(15b)计算的结果具有一定的差别,在低冲泻区两公式计算的结果均高估了实验结果,且式(15a)计算得到的结果更大;而在中、高冲泻区内,式(15b)计算得到的结果更接近实验值,两公式计算差别的具体分界点对应于Case1:x/Rx<0.24、Case2:x/Rx<0.3、Case3:x/Rx<0.3、Case4:x/Rx<0.2,即在分界点的离岸区域,式(15a)计算的结果更接近实验值,而在分界点的向岸区域式(15b)的计算结果更优。因此,在本文实验条件下,对于式(15),L的取值范围为:0.2~0.3,即分界点位于低冲泻区和中冲泻区的衔接段。综上可知,采用不同公式分段进行冲泻区的推移质输沙率是可行的,结果更为可靠,在本研究后续研究(第II部分)中进行岸滩剖面变化计算中也得到了证实,由于篇幅问题在此不再详述。

图4 输沙率计算过程(Case1,x=1.5m)
4 结论
近岸带冲泻区往复急变薄层水流作用下床面泥沙运动过程非常复杂,以致现有冲泻区泥沙输运函数大多是借鉴河流输沙理论中基于能量形式的公式。根据本研究,得到以下结论:
(1)考虑渗流流速、主流产生的垂向流速对冲泻区泥沙运动床面剪切应力和有效重度改变效应,结合岸滩坡度的影响,分析得到了符合冲泻区水沙动力特征的瞬时希尔兹参数计算公式,能够反映上举力、拖曳力、摩擦力、重力和渗流力等对颗粒运动状态的影响,并给出了所含参数的计算方法。
(2)依据低、中冲泻区输沙强度由流速主导、高冲泻区输沙强度由水深主导的关系,建立了可描述冲泻区薄层水流下泥沙运动的分段输沙模式,并基于实验数据拟合得到本实验条件下分段参数L的取值,计算结果表明采用分段进行冲泻区的推移质输沙率计算是可行的。
与此同时,由于冲泻区床面泥沙输运过程十分复杂,本研究对一些参数计算做了适当简化。例如,在摩阻系数的计算中并未完全考虑动态摩阻系数。此外,目前关于波浪作用下近岸带床面泥沙运动的输沙模式仍然难以采用通用的输沙模式,特别是在泥沙运动呈现Sheet flow运动形式时。因此,现阶段采用分段推移质输沙率计算公式并基于水槽实验率定的方式确定分段参数是一种较为有效的处理方法,提出适应于近岸带泥沙运动的通用输沙模式将是未来研究的方向。

图5 不同工况下净输沙率计算值与实验值的沿岸分布

