风暴浪作用下沙质岸滩稳定机制物理模型试验研究*

王 俊 尤再进 梁丙臣

风暴浪作用下沙质岸滩稳定机制物理模型试验研究*

王 俊1尤再进1①梁丙臣2

(1. 大连海事大学港口与航运安全协同创新中心 辽宁大连 116026; 2. 中国海洋大学 山东省海洋工程重点实验室 山东青岛 266100)

近年来风暴潮等海洋灾害日趋频发, 沙质海岸侵蚀问题也愈发突出, 沙滩稳定防护显得日益重要。为研究风暴浪作用下沙质岸滩稳定机制问题, 设计了一系列的水槽试验, 对风暴浪作用下沙质岸滩的稳定机制和演变过程进行了录像观察和研究分析。试验中采用图像处理技术, 根据水和岸滩床面的像素值差异, 对岸滩整体剖面进行实时动态提取; 对比和分析了不同入射波高、波周期、水深、岸滩初始坡度以及波高连续变化下沙质岸滩演变过程。试验结果表明, 岸滩稳定与岸滩初始坡度和沙坝的发育直接相关, 而波参数主要影响岸滩扰动幅度和沙坝以及前滩侵蚀边界的位置变化。当入射波高连续变化时, 沙坝迅速响应并向离岸迁移。岸滩变化幅值与入射波能流存在明显正相关关系, 波能流越大对岸滩稳定性的危害越大。而水位升高会增强前滩向岸侵蚀风险。此外, 在本试验尺度下, 前滩以侵蚀为主。当岸滩初始坡度小于稳定坡度且波陡较小时, 即Dean参数′较小时, 岸滩才发生明显的前滩淤积, 这对于试验尺度下岸滩恢复工况研究至关重要。具体来说, 当岸滩整体坡度为1:10且前滩坡度达到1:5～1:2.5时, 岸滩稳定性最好, 岸滩形态最接近最终平衡剖面, 岸滩趋于稳定的时间最短。

岸滩; 水槽试验; 初始坡度; 波参数; 稳定性; 演变; 图像处理

沙质岸滩作为海岸带中的黄金海岸, 是优质的滨海旅游场所, 全球18%和中国30%的大陆海岸线均为沙质岸滩, 有着极其重要的经济和社会价值。但由于沙质海岸地处海陆交互作用地带, 环境敏感性较高, 侵蚀风险也尤为突出。我国作为遭受风暴潮灾害最多的国家之一, 平均每年有10余次台风经过, 近20年来近一半年份的经济损失超过100亿元, 风暴潮等自然灾害所造成的海岸侵蚀问题已成为我国沿海地区可持续发展的严重阻碍(2002～2020年中国海洋灾害公报)(中华人民共和国自然资源部, 2003～2021)。风暴潮诱发的强浪、增水等极端海况作用, 直接导致向岸波浪强度增大(蒋昌波等, 2014, 2017), 原有岸滩平衡受强非线性动力过程破坏, 使得在原有水深较浅的海滩发生波浪破碎、强烈紊动, 可在短时间内引起大量泥沙运动, 产生的回流挟带泥沙离岸运动, 致使岸滩会出现不可逆的侵蚀。针对侵蚀海岸线, 进行人工补沙和养滩养滨, 详细研究波浪作用下岸滩剖面向平衡剖面, 保持沙质海岸稳定性, 确定人工补沙位置、补沙量、防护物筑构位置等工程问题, 均具有十分重要的经济、生态和社会价值。

从近岸泥沙横向输移上看, 一部分流失的泥沙离岸堆积形成沙坝, 抑制向岸侵蚀进一步加剧; 一部分受底部回流挟带传至深水处, 致使此部分沙滩泥沙完全流失, 如Seymour等(2005)长期测量美国加利福尼亚州南部Torrey Pines State海滩发现, 在2001年11月的一次风暴潮后, 近岸391 000 m3泥沙被侵蚀, 只有80%的侵蚀泥沙离岸堆积, 而剩余20%或者相当于该沙滩0.06 m平均厚度的泥沙完全流失。同时, 不同区域的现场实测研究也从不同角度, 证明了风暴潮对岸滩侵蚀的危害程度(Karunarathna, 2014; 李明杰等, 2015; 蒋昌波等, 2017)。目前对岸滩现场地形的动态提取较难, 主要难点在于对岸滩剖面高精度同步测量, 受现场观测方法限制, 对岸滩研究多基于静态统计分析, 而对岸滩冲淤演变过程研究较少。通过对大量岸滩实测剖面的统计分析, Dean (1977, 1991)认为岸滩平衡剖面主要与泥沙粒径相关, 并提出Dean平衡剖面预测公式。Larson等(1995)指出平衡剖面下, 沙坝体积与入射波有关。Türker等(2006)发现岸滩初始坡度不同, 即使粒径、入射波相同, 岸滩最终平衡剖面也明显不同。Baldock等(2010, 2011)、蒋昌波等(2015)在实验水槽内研究单色波、双色波、长波、波群、随机波等不同类型波浪对岸滩影响。

但是, 由于试验尺度对测量精度要求更高, 传统实测方法应用于实验室尺度测量仍然存在较多问题, 尤其对于破碎区, 传统侵入式测量方法通常会出现信号缺失等问题(Chardón-Maldonado, 2016; Puleo, 2016), 而且导致对岸滩演变过程的人为扰动, 试验研究效果并不理想。因此, 本文通过视频图像分析的方法, 实现了对断面水槽岸滩演变过程中岸滩剖面数据的高精度和无干扰的动态观测, 并基于不同工况岸滩剖面实时观测, 探究波参数和岸滩初始坡度对沙质岸滩稳定性和岸滩冲淤趋势的重要影响。

1 试验概况

1.1 试验设备与仪器布置

本文开展两次室内水槽试验(试验1和试验2), 分别在山东省海洋工程重点实验室的两个断面水槽中进行, 试验1水槽具体参数为: 水槽总长为60 m, 除去造波段和消波段水槽实际试验长约50 m、宽3 m、高1.5 m。为方便试验过程观测监控, 水槽两侧分别由28块宽1.4 m、高1.4 m的透明钢化玻璃组成, 为保证水槽侧壁强度, 玻璃四周由宽0.1 m的钢筋条固定。试验2水槽总长为30 m, 除去造波段和消波段水槽实际试验长约28 m、宽0.6 m、高1.0 m, 与试验1水槽相似, 水槽两侧分别由23块宽1.2 m、高1.0 m的透明玻璃组成, 每块玻璃由宽0.1 m的钢筋条固定并两两相连。

本文试验均选用平直均匀坡度岸滩作为初始剖面, 在不同坡度下, 波浪破碎类型、地形演变趋势以及爬坡特点均不相同, 特别是冲泻区作为最大爬高与最大落深之间区域, 其最大落深在耗散型岸滩中高于波浪增水, 反射型岸滩中低于波浪增水。在试验1中, 前滩选取1:5和1:15两种坡度, 前滩顶高均为0.8 m, 坡顶布置高0.5 m坡度为1:3的陡坡延伸段(水平长度1.5 m), 用以模拟自然岸滩上端沙丘, 模型末端顶高为1.3 m; 水平方向从距造波机14.5 m处向岸布置10个波高仪, 20个压力传感器, 4个声学多普勒流速仪(acoustic doppler velocimetry, ADV); 由于试验为动床底床, 部分工况在试验过程中, 底床在破碎区形成沙坝而抬高, 底床在冲泻区出现侵蚀而降低, 为在试验中更接近冲泻区水动力测量, 传感器具体位置会随每种工况的变化而进行具体调整, 试验岸滩模型及传感器大致布置方式如图1a所示。本文的试验2在试验1基础上, 引入=1:5,=1:7,=1:10,=1:12,=1:15多种岸滩坡度, 详细探究岸滩初始坡度对岸滩冲淤趋势和平衡稳定速度影响, 水平方向从距造波机18.25 m处向岸布置5个波高仪, 2个ADV, 具体仪器布置如图1b。

试验波高仪及压力传感器采用中交天津港湾工程研究院生产电容式波高仪、空隙压力传感器, 传感器与DS-30型智能测波仪及数据采集系统配合工作, 该采集系统具有实时监控、数据采集、数据处理等多项功能, 可以满足波浪试验中数据采集的各种要求, 采样频率可控, 试验中采用20 Hz进行测量。流速仪采用Nortek公司开发和生产的小威龙流速仪, 测量精度可达±1 mm/s, 采样频率可控(1～200 Hz), 试验中采样频率为50 Hz。为方便试验描述, 将试验水槽建立为二维笛卡儿坐标系, 以造波机与水槽底部相交处位置作为坐标轴原点以波浪传播方向为轴正方向, 以水深增加方向为轴正方向。

本试验中采用PointGrey公司生产的高速工业相机, 相机分辨率2 048×2 048, 帧率可调, 对试验过程进行侧向观测, 并采用图像处理技术实现岸滩剖面和自由液面实时动态提取。侧向相机观测系统试验现场布置如图2所示。在试验中, 在较高悬沙浓度的情况下, 为提高观测区域水沙交界面的分辨效果, 在相机观测区域正上方布置探照灯, 对观测区域进行打光。

1.2 试验工况

试验1和试验2分别选取中值粒径为50=0.21、0.36、1.07和0.21 mm, 涵盖了细砂(0.10～0.25 mm)、中砂(0.25～0.5 mm)、粗砂(0.5～2 mm)三种类型自然砂进行试验。试验1包括50=0.21、0.36、1.07 mm (粗、中、细)三种中值粒径试验沙, 试验2采用中值粒径50=0.21 mm (细砂)进行试验, 由于试验为均匀沙输运机理研究, 试验沙分选度分别为1.26 (试验1:50=0.21 mm)、1.24 (试验1:50=0.21 mm)、1.43 (试验1:50=0.21 mm)和1.12 (试验2:50=0.21 mm), 均处于较好分选度的范围, 表明模型沙颗粒比较均匀, 且为方便视频观测和分析, 泥沙经过精细筛选且在加入水槽试验前先用水清洗干净并烘干, 排除杂质对试验观测影响。

图1 试验布置示意图

注:表示岸滩坡度角; tan表示岸滩坡度, tan=1:5/1:15表示1:5和1:15两种坡度; STL表示静水位, 0.5/0.7 m表示0.5 m和0.7 m两种水深

图2 试验中相机观测系统现场布置

试验以规则波为主, 以便详细对比分析不同动力参数对岸滩影响规律。依据实验室造波机的性能参数, 试验1选取0.1和0.2 m两种波高, 1.2、2.1、3.0 s三种周期进行试验。考虑到模型前滩顶高0.8 m, 沙丘顶高1.3 m, 试验选取两种0.5和0.7 m两种概化水位, 0.5 m水位代表低潮时的情况, 通常情况下波浪上冲过程难以对沙丘造成影响, 沙丘形态和体积变化概率较小; 而0.7 m代表高潮水位(风暴增水), 沙丘底标高距离静水位只有0.1 m, 在波浪爬高的作用下很容易对沙丘产生影响, 此时沙丘形态和体积变化概率较大。同时, 根据造波机冲程与输出波高之间关系, 如公式(1)所示, 通过对造波机冲程控制, 保持周期不变, 成功实现了对风暴潮期间波浪强度递增、递减连续变化过程, 使波高进行先递增后平衡最后递减的变化趋势, 模拟风暴浪变化过程。整个风暴浪过程, 包括20 min波高连续递增, 20 min波高平衡, 20 min波高递减, 总计1 h (Wang, 2020):

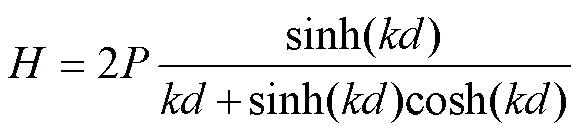
其中, H为造波机输出波高, P为造波机冲程, 波数k是水深的函数(You, 2008), d为水深。由于不同坡度岸滩对造波机二次反射差异, 相同造波机冲程下, 相较于S=1:15坡度岸滩, S=1:5坡度岸滩由于坡度陡, 对波浪反射作用更为显著, 进而对造波机二次反射问题也更为明显, 而S=1:15坡度岸滩由于坡度缓, 大部分波能在破浪近岸浅化、破碎以及上爬过程中耗散掉,对造波机二次反射问题较S=1:5坡度岸滩弱很多, 因此, S=1:15坡度岸滩中实际测得波高变化过程更接近于理想变化过程(图3)。

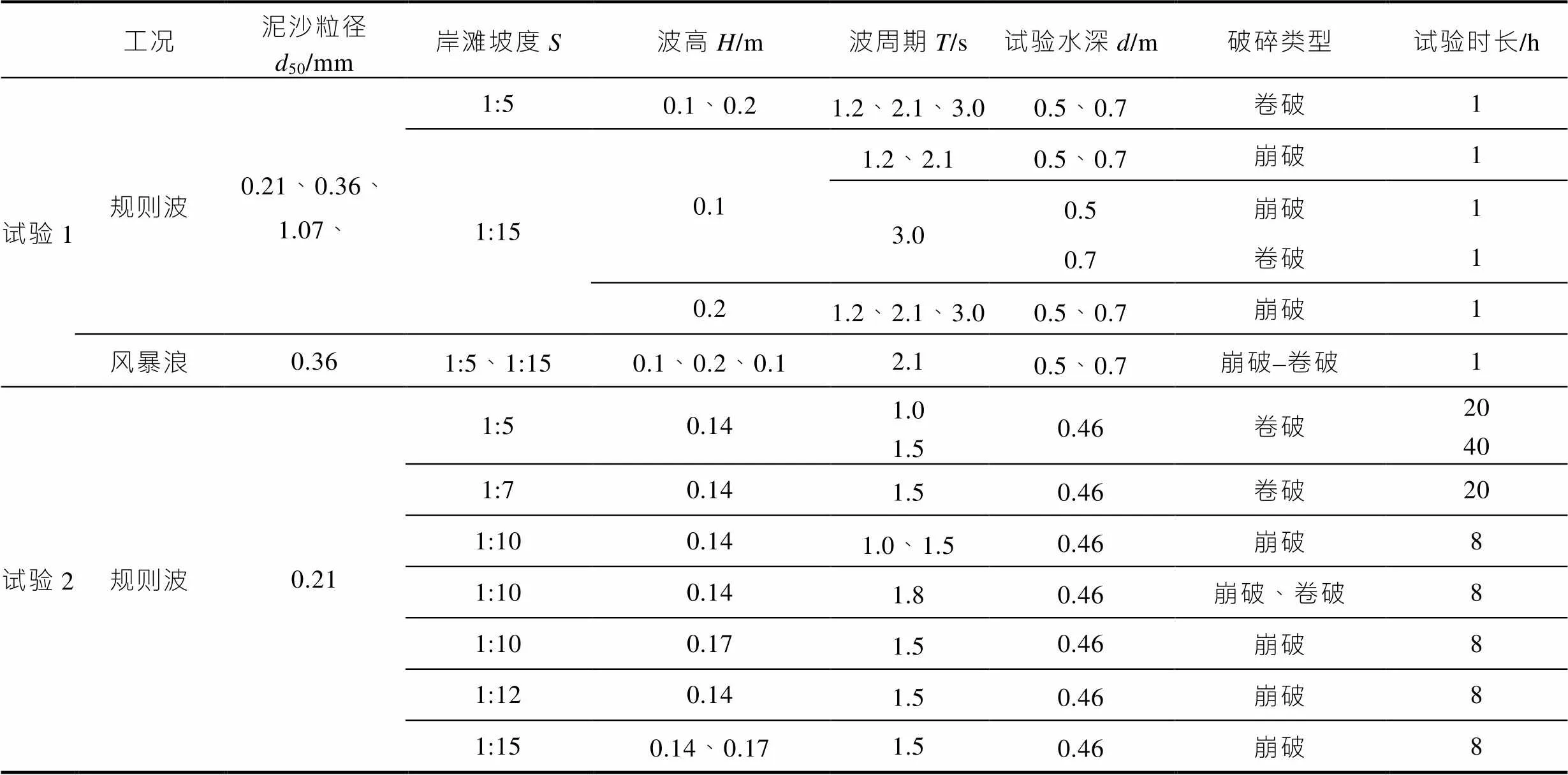
由于岸滩整体演变过程较慢, 试验1过程中当波浪作用1 h后岸滩演变速率明显减弱, 甚至部分工况岸滩相对稳定, 认为岸滩已趋近于平衡, 试验1造波时长均在1 h左右。因此, 在保障试验中岸滩达到相对稳定状态的条件下, 考虑试验周期成本, 试验中各工况造波时间均控制在1 h左右。在每组试验结束后, 均进行人工地形复原, 保证初始地形为相同的1:5或1:15均匀坡度。基于试验2试验水槽造波条件, 选取1.0、1.5、1.8 s三种周期和0.14、0.17 m两种波高进行规则波常浪组合。通过对试验1结果初步分析, 岸滩初始坡度对岸滩演变趋势和稳定性都有明显影响, 且规则波作用1 h后岸滩形态仍呈现明显变化趋势。为此, 试验2详细研究了不同岸滩初始坡度对岸滩演变特征影响, 并通过增加规则波作用时长, 更准确探究岸滩平衡演变过程。本文实验发现,=1:10,=1:12,=1:15初始坡度可较快达到稳定, 常浪作用时长为8 h左右, 而对于=1:5、=1:7初始坡度岸滩稳定速度较慢, 常浪作用时长为20～40 h。此外, 针对风暴潮过程中强浪、增减水等极端海况作用下向岸波浪强度和水位变化, 岸滩侵蚀、风暴潮后岸滩恢复再平衡整个动态演变过程, 对比风暴潮对岸滩突变特变作用特点, 试验2也增加了“常浪-风暴潮-常浪”工况, 探讨常浪作用平衡岸滩在风暴潮作用下冲淤演变特点及风暴后常浪再恢复过程。水深设置方面选择0.46 m为常浪水深和0.56 m为风暴潮高水深, 风暴潮增减水的三个演变过程(0.46 m-0.56 m-0.46 m)。风暴潮由1 h增水-1 h高水位-1 h减水过程组成, 共计造波时长3 h。试验1和试验2工况具体见表1。

表1 试验波浪工况

Tab.1 Specifications of the wave cases

注: “–”表示缓变过程

为了方便本文的工况注释, 分别采用G代表粗砂、M代表中砂、F代表细砂; S05、S07、S10、S12、S15分别代表初始坡度=1:5、=1:7、=1:10、=1:12、=1:15岸滩; 同理, H10、H14、H20分别代表波高=0.1 m、=0.14 m、=0.2 m; T10、T12、T15、T21分别代表波周期=1.0 s、=1.2 s、=1.5 s、=2.1 s; d4、d5、d7分别代表试验水深=0.46 m、=0.5 m、=0.7 m。基于以上的工况注释, MS15H10T21d5代表试验1中的一种工况为: M中砂50=0.36 mm, 岸滩初始坡度=1:15, 波高=0.1 m, 波周期=2.1 s, 试验水深=0.5 m, 而FS05H14T15d4代表试验2中工况: F细砂50=0.21 mm, 岸滩初始坡度=1:5, 波高=0.14 m, 波周期=1.5 s, 试验水深=0.46 m。

2 沙滩剖面数据采集

常用地形观测方法主要基于超声波、声呐、激光等原理, 其中超声波底床传感器(acoustic displacement sensor, ADS)是底床高程实时观测的主要方法, 但该方法为单点侵入式测量, 为获得更高的空间分辨率, 需要布置足够多的传感器, 必然会影响观测区域流场且存在信号缺失等问题, 特别对于试验尺度下破碎区和冲泻区地形测量(Puleo, 2016)。Atkinson等(2016)将激光雷达应用于试验尺度下底床剖面实时扫描中, 此方法可以透过水介质进行非侵入实时剖面测量, 但地形扫描过程中, 仍存在测量不同步的缺点。因此, 一种高精度非侵入式、适用于试验尺度的剖面动态测量方法亟待开发。基于上述问题, 本试验采用一种相机(摄像机)结合断面水槽的岸滩剖面实时观测方法。该方法以图像处理技术为核心, 通过对侧向观测相机拍照进行逐帧图像处理, 实现对试验岸滩剖面的实时动态提取, 相机帧率10 帧/s, 分辨率2 048×2 048, 主要流程包括:

(1) 相机标定: 通过对打印好的黑白棋盘进行多角度拍照, 提取每张标定图片的角点信息, 求得相机自身的内参矩阵, 去除每台相机成像畸变, 将原有扭曲图像展平, 并基于提前布置好的校正点, 建立图像内像素点的空间位置校正关系, 如图4所示。

(2) 像素点空间校正: 试验前在相机拍摄范围内的水槽玻璃侧壁平行布置4～6个黑白方格, 并以方格中心作为校正点, 其中水平方向2个, 垂向2～3个, 校正点之间横向距离为1或2 m, 垂向距离为0.8 m。基于提前布置好的校正点, 建立图像内像素点的空间位置校正关系(图4)。

(3) 图像后处理分析: 边界识别算法的优化和程序编写, 基于水、沙、气介质像素值的差异, 实现了岸滩剖面和自由液面的同步提取(图5)。为保障数据可靠性, 通过本文岸滩演变试验剖面动态观测方法测量岸滩剖面和自由液面数据与传统观测仪器全站仪和波高仪数据进行了对比(图6), 二者数据基本吻合数据可靠。进一步展现了图像观测技术在岸滩演变试验中的应用前景, 保障了地形数据和水动力数据的同步性。

图4 校正网格照片及交点处像素提取

注: 括号中的数字表示黑白格中心点在空间坐标系实际坐标(单位: m)

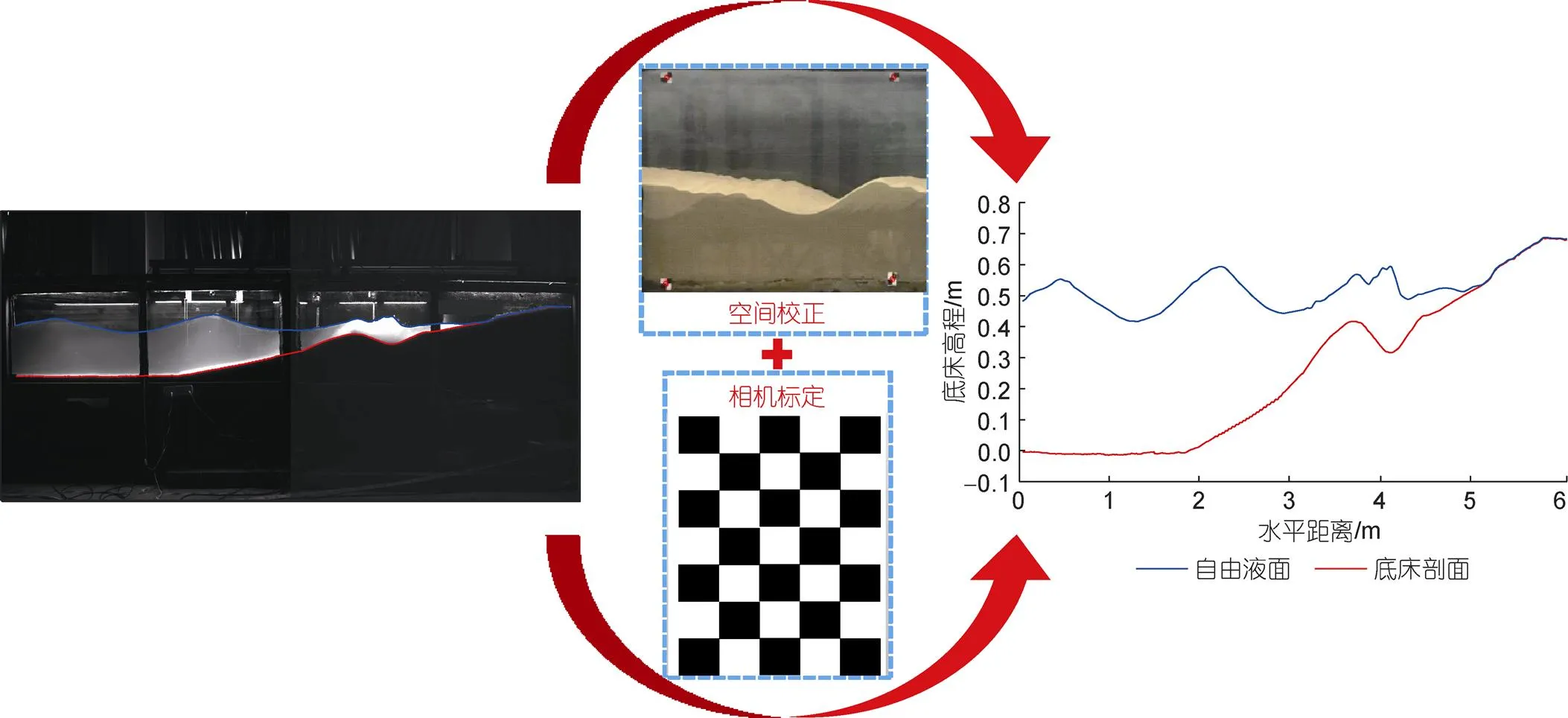
图5 图像处理校正流程

由于试验时长较长(每组工况均保持1 h以上波浪作用), 为节省存储空间, 相机帧率调至10帧/s, 该帧率完全满足在试验设计工况下, 波周期内采样次数大于10的基本要求。此外, 由于试验获得图像分辨率为2 048(垂直)×2 048(水平), 根据不同初始坡度岸滩中相机水平观测范围, 如=1:5、=1:10岸滩模型每台相机观测范围为2.6 m, 而=1:7、=1:12、=1:15岸滩模型每台相机观测范围为3.5 m, 因此, 试验岸滩剖面空间分辨率为1.2 mm (=1:5、=1:10岸滩模型)和1.7 mm (=1:7、=1:12、=1:15岸滩模型)。

3 结果及分析

在现场实测条件下, 定量对比分析不同海况影响下岸滩响应差异研究往往较难, 主要有两个主要原因: 自然条件下岸滩初始地形无法保证一致,波参数、静水面高度等动力参数不稳定。且由于现场实测技术限制, 往往较难获取岸滩演变过程中实时剖面数据提取。而在室内试验条件下, 能够通过控制水动力参数和地形参数变量, 全面分析泥沙粒径、岸滩初始坡度、沙坝发育等地形参数以及波高、波周期、水深等水动力参数对沙质岸滩横向冲淤影响规律, 诠释不同水动力参数和地形参数组合条件下近岸剖面演变过程的稳定机制。

图6 图像观测方法实测剖面以及自由液面数据与全站仪和波高仪测量验证效果

3.1 波浪要素对沙滩演变影响

初始坡度均匀的沙质海滩剖面在波浪作用下, 悬浮大量泥沙, 随波浪作用定向输移, 剖面快速响应,经过充分长时间恒定波浪作用后, 地形演变速度会逐渐减缓, 此时海滩形态与入射波条件相互适应, 岸滩逐渐趋于稳定, 地形不再明显变化或在某一稳定状态往复波动, 此时海滩剖面达到平衡剖面。基于试验1和试验2规则波试验数据, 本文对不同入射波高、波周期及水深影响下, 岸滩演变特征进行了对比分析。

根据规则波试验剖面和底床相对初始高程变化, 如图7～9, 其中, 每组工况图上、中、下分别表示每分钟岸滩剖面时程变化和等间隔不同时刻岸滩剖面对比以及实时床面相对于初始床面变化量, 其中上窗口3D图中剖面时间步长1 min, 随时间变化剖面颜色由浅灰色变为深黑色, 而下窗口实时床面高程变化图中蓝色表示床面侵蚀深度, 红色表示床面淤积高度。恒定入射波作用下, 均匀坡度人工岸滩以沙坝为界, 岸滩剖面呈明显的单调性变化, 即前滩以侵蚀为主, 前滩侵蚀的泥沙在离岸浅水区不断堆积, 致使浅水区和外破碎区床面不断抬高, 形成沙坝, 且随波浪持续作用, 前滩侵蚀不断加剧, 沙坝不断离岸迁移生长, 随着沙坝发育发展, 沙坝逐渐发挥对前滩的保护作用, 前滩侵蚀速率明显减缓, 岸滩逐渐趋于稳定,所以, 试验中前滩变化幅度最大的阶段往往出现在试验开始阶段, 沙坝的发育发展对岸滩剖面稳定性至关重要。

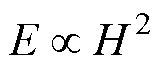
如图8所示, 与不同波高影响下岸滩演变情况相似, 不同入射波周期下, 岸滩稳定后也呈现沙坝型剖面特点, 岸滩总体呈现岸滩持续向岸侵蚀范围且垂向侵蚀深度增大、坡脚浅水区淤积并形成明显沙纹以及沙坝离岸运动并沙坝逐渐抬高等现象, 前滩向岸侵蚀范围以及浅水区床面扰动均随波周期增大而增大。当波周期增大时, 由于波周期较大, 波陡较小, 波浪不易破碎, 相同岸滩初始坡度下, 破碎点随波周期增大而向岸移动, 岸滩稳定后沙坝位置也随破碎点向岸移动更趋于向岸方向, 如图8a～8d。对比前滩侵蚀体积、向岸侵蚀距离以及浅水区床面扰动情况, 波高和波周期影响符合能量变化, 即当波高波周期较大时,单位波长波能更大, 对岸滩整体扰动更剧烈,对前滩侵蚀风险也更大, 岸线蚀退距离也更大。

注:50表示试验沙中值粒径,表示波高,表示波周期,表示水深,表示岸滩初始坡度,表示试验时间

已有研究表明海平面上升或静水面位置变化是引起海岸动力作用强度不同是破坏岸滩稳定的另一个重要因素。目前普遍认为, 海平面上升主要通过两种方式引起岸滩侵蚀问题, 一种是海平面上升直接淹没原有陆地, 使侵蚀基面升高, 造成岸线的整体侵退, 向岸侵蚀距离增大; 另一种为海平面上升, 原有水深改变, 原始浅水区水深升高, 近岸动力条件增强, 原有海岸水沙平衡被破坏, 加剧了岸线的侵蚀, 沙丘侵蚀体积增大(蒋昌波等, 2017)。如图9所示, 本试验不同水位下岸滩演变也存在相同特点, 不同水位下, 岸滩整体变化特征基本一致, 主要区别在于沙坝位置和前滩侵蚀距离的变化, 此外, 沙坝附近滩面淤积高度也存在差异。由于岸滩初始坡度=1:5, 当水位=0.7 m较大时(图9b), 与=0.5 m相比(图9a), 水位升高0.2 m后, 静水面与岸滩交界面向岸移动了约1 m, 而稳定后前滩侵蚀范围也随之明显增大, 侵蚀岸线也增加了约1 m, 同时, 由于水深增大, 原破碎点附近当地水深变大, 波浪破碎滞后, 破碎点也向岸移动, 更多波能可作用至更远的向岸区域, 可能导致更多前滩泥沙流失, 因此除岸滩稳定后沙坝位置明显向岸移动外, 沙坝附近床面抬高高度也更大, 表明更多前滩侵蚀泥沙离岸堆积, 水位增大后对岸线破坏风险增大, 进一步验证了已有研究。

通过将上文不同波参数下岸滩剖面稳定特征进行对比, 可认为在与本试验相近的中小尺度水槽内, 波参数差异对岸滩横向冲淤关系和稳定后岸滩剖面特征影响较小, 当岸滩初始坡度≥1:10较陡时(具体见3.2节), 相同岸滩初始坡度下, 岸滩平衡剖面特征基本一致, 均呈现前滩侵蚀、岸线蚀退同时前滩侵蚀泥沙离岸淤积, 岸滩稳定后均呈现出明显的沙坝型剖面特点, 波参数变化对岸滩影响主要表现于对岸滩床面扰动幅度、沙坝特征、前滩侵蚀强度以及岸线蚀退位置变化, 岸滩稳定后沙坝位置变化趋势与波参数导致的破碎点位置变化趋势一致, 即破碎点位置直接决定岸滩稳定后沙坝位置。

3.2 岸滩初始坡度对沙滩演变影响

本节针对不同岸滩初始坡度岸滩稳定性问题, 对比分析岸滩初始坡度由=1:5到=1:15变化时, 岸滩剖面向平衡状态演变过程, 如图10所示。虽然波况、泥沙粒径均与试验1不同, 但试验2和试验1中初始坡度=1:5岸滩均呈现相同的岸滩冲淤变化规律, 如图10a中=59 min时刻岸滩剖面与试验1中初始坡度=1:5岸滩剖面稳定特征相似, 均呈现前滩侵蚀岸线明显蚀退, 在水下破碎点附近产生大幅度淤积, 形成明显的沙坝型剖面, 同时, 波浪作用前期岸滩剖面变化速率最快, 随着离岸沙坝形成, 岸线侵蚀速度明显变缓。相较于试验1波浪作用时间较短, 试验2波浪作用时间更长, 可更明显地看出反射型剖面(初始坡度较陡)向平衡状态的调整过程, 前滩侵蚀泥沙首先在破碎点淤积形成沙坝, 但此时岸滩远远未达到稳定状态, 沙坝并不稳定, 前滩侵蚀的泥沙可随着沙坝迎浪面越来越陡进一步离岸淤积, 此处尽管水深较大、波浪未破碎, 波浪作用明显较弱, 但在重力和波浪共同作用下, 泥沙会不断向海流失堆积, 致使起坡点也不断向海延伸, 这个过程时间历程较长, 因此, 在试验1中并未观测到, 特别当岸滩初始坡度较陡时, 如=1:5和=1:7。在前滩侵蚀和侵蚀泥沙离岸堆积起坡点向海延伸的共同作用下, 整个岸滩剖面坡度不断变缓。虽然在波浪作用60 min后, 得益于离岸沙坝的防护作用, 整个剖面变化明显放缓, 但整个岸滩仍处于侵蚀状态, 岸线不断后移。

随着岸滩初始坡度变缓, 相同波况下, 当岸滩初始坡度为=1:7时, 岸滩剖面整体冲淤特性基本与=1:5时相同, 如图10b所示, 仍为前滩侵蚀, 侵蚀泥沙在离岸浅水区堆积形成沙坝与床面抬高, 淤积范围在持续波浪作用下逐渐扩大, 大量泥沙向坡脚运动, 造成剖面底部高程增大, 坡脚向海延伸, 最大淤积高度0.1 m。但相较于初始坡度=1:5岸滩, 岸滩变化幅值明显减弱, 最大冲刷深度变为0.18 m, 岸滩在1 000 min (17 h左右)后更快达到相对稳定状态。

当岸滩初始坡度进一步变缓至=1:10时, 相同波况作用下, 岸滩剖面变化程度以及岸线区域趋于稳定效率明显提高, 岸线侵蚀以及坡脚位移明显减小, 表明该坡度岸滩剖面已经比较接近于平衡剖面坡度。如图8b, 与初始坡度=1:5、=1:7岸滩变化相似, 前滩产生剧烈侵蚀, 表现为沙坝向岸方向冲刷槽的形成和岸线蚀退, 最大冲刷深度进一步减小至0.16 m, 但与初始坡度=1:5、=1:7岸滩变化形成显著差异是, 虽然前滩出现明显侵蚀并导致岸线后退, 但在岸线向岸侧(≈5.7 m,<300 min)同时出现了少量淤积情况。当波浪作用480 min (8 h)左右后岸滩就基本稳定, 前滩侵蚀深度向岸侵蚀范围不再发生明显变化, 最大冲刷深度变为0.15 m。

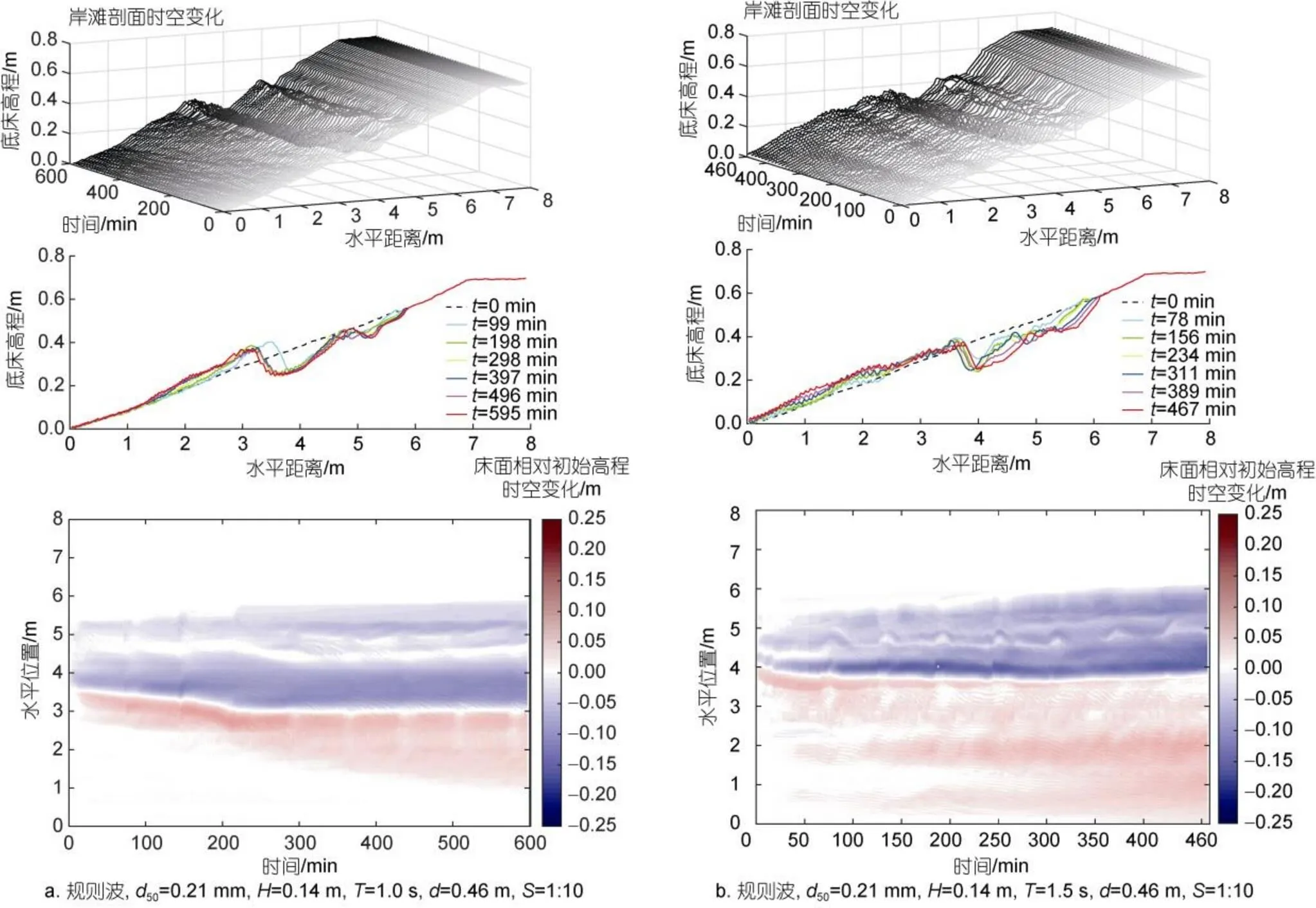
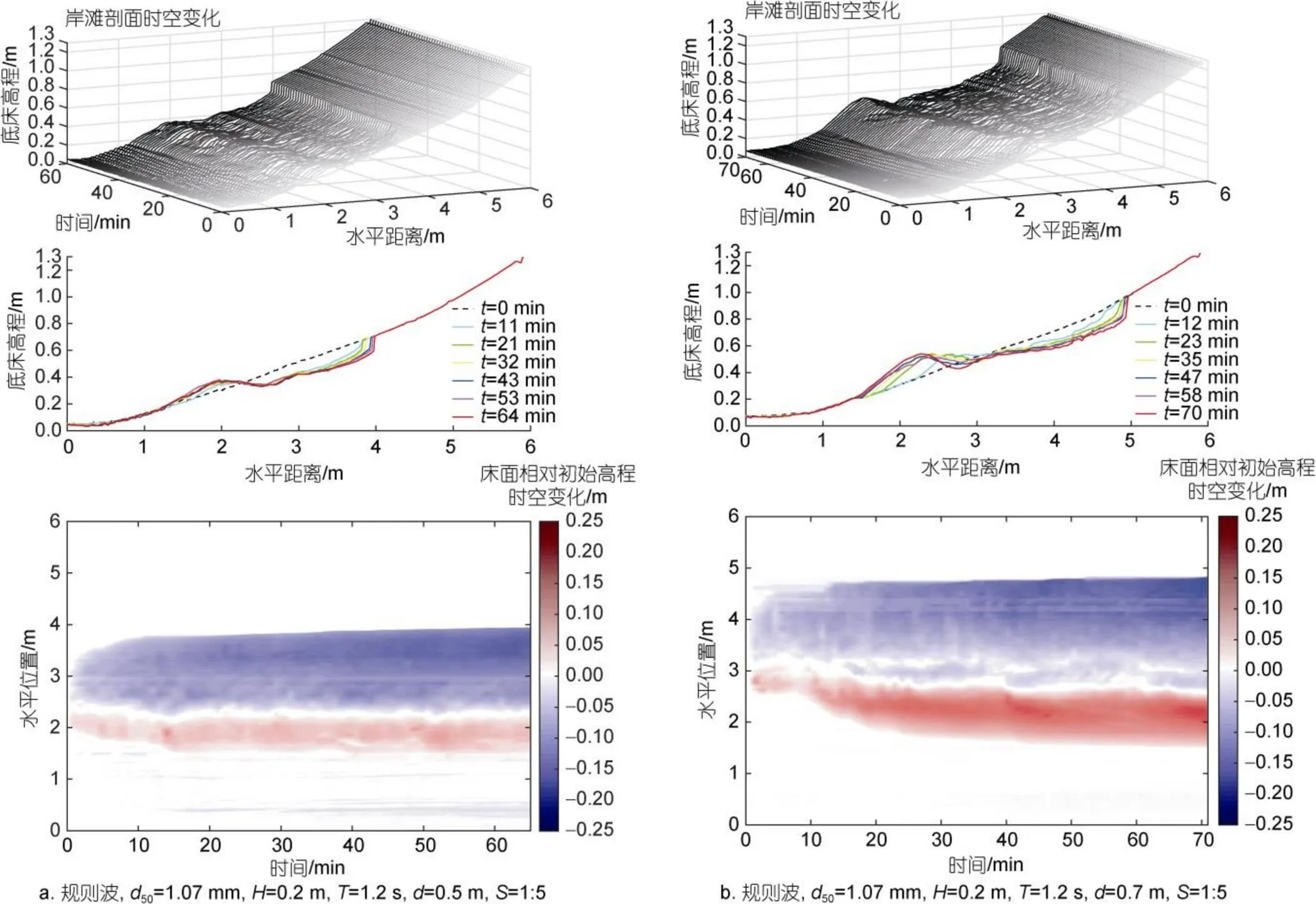
图9 不同水位下岸滩演变过程

由此可见, 当岸滩初始坡度达到=1:10时, 岸滩稳定性发生了明显改变, 相较于岸滩初始坡度=1:5和=1:7, 坡脚处地貌变化发生特点明显改变, 不再出现明显的离岸泥沙不断向海淤积、坡脚向海延伸现象, 尽管前滩仍然出现明显侵蚀, 但侵蚀程度明显小于岸滩初始坡度=1:5和=1:7, 且在试验中后期, 岸线不再发生明显后退, 且地貌不再发生明显变化, 表明岸滩达到了相对平衡状态。为进一步论证岸滩初始坡度在何种范围内更容易达到平衡状态、稳定性更高, 进一步补充了两种更缓坡度岸滩初始坡度=1:12和=1:15。如图10c、10d所示, 岸滩初始坡度=1:12和=1:15时, 岸滩演变特点与岸滩初始坡度=1:10时演变特征更为相似, 岸滩主要变化集中在前滩剖面调整, 同样未出现明显的坡脚处向海淤积问题。因此, 可认为波浪作用时, 滩面泥沙基本完全保留于整个闭合剖面内, 保障了整个剖面稳定性。此外, 当岸滩初始坡度较缓时, 在波浪上冲边界(岸线向岸侧)会出现更明显的淤积, 如初始坡度=1:12时(≈6.5 m,<400 min)、初始坡度=1:15时(≈6.5 m,<450 min), 由于坡脚位置不变, 岸滩整体坡度趋陡, 证明岸滩稳定坡度应介于=1:10和=1:12之间。

初始坡度=1:12和=1:15时, 相对于岸滩初始坡度=1:10 (图8b), 前滩侵蚀程度以及岸滩剖面变化程度明显减弱, 且相较于初始坡度=1:10和初始坡度=1:15, 当初始坡度=1:12时, 前滩侵蚀程度、破碎点至坡度岸滩剖面变化均明显更小。通过对相同条件下不同坡度岸滩演变特征对比分析, 可认为在本文试验条件下, 当岸滩初始坡度<1:10时, 初始岸滩坡度设计已经比较利于岸滩高效趋近于平衡剖面, 且当初始坡度=1:12时更接近于平衡剖面坡度, 并不是坡度约缓越利于岸滩更高效达到平衡状态。

试验条件下, 岸滩剖面稳定速率与岸滩初始坡度密切相关。初始坡度越接近最终平衡剖面平均坡度或初始地形越接近平衡剖面形态的试验岸滩剖面, 均可在不同侵蚀波况的动力作用下快速达到相对稳定状态; 相反, 当初始地形与最终平衡剖面相差较大, 如本试验中岸滩初始坡度=1:5与=1:7的岸滩模型则需在较长时间的波浪作用下, 通过前滩和起坡点剖面调整岸滩整体坡度, 使其逐渐趋近于平衡剖面坡度, 才能使地形地貌条件与水动力条件相互适应, 从而达到地形不再受波浪影响而发生明显变化的稳定状态。

3.3 滩肩型剖面形成条件

由上文可知, 对于本文试验1和试验2中小尺度试验水槽中岸滩演变试验, 波浪条件和岸滩初始坡度均对岸滩演变特点有明显影响, 其中, 波参数影响主要表现于岸滩稳定后沙坝位置变化, 而岸滩坡度对岸滩稳定性至关重要, 因此, 不同初始坡度岸滩在波浪作用下均会通过泥沙横向输移驱使岸滩坡度逐渐趋近于相似的稳定坡度, 而当岸滩初始坡度较陡>1:10 时, 通过前滩侵蚀离岸淤积调整岸滩整体坡度至稳定坡度更为常见。但受限于造波条件限制, 如本试验1水槽规则波造波极限<0.25 m,<3 s, 试验2水槽规则波造波极限<0.2 m,<2 s, 不同工况组合下, 岸滩横向冲淤规律以及最终平衡剖面类型基本一致, 即前滩侵蚀, 侵蚀泥沙离岸过渡区淤积形成沙坝并抬高浅水区床面, 最终演变成沙坝型剖面, 较难出现明显的滩肩型剖面。

如图11所示, 当入射波=0.1 m,=3.0 s,=0.7 m时, 尽管在初始坡度=1:5岸滩上岸滩冲淤趋势与前文工况一致, 仍以前滩侵蚀离岸淤积形成沙坝型剖面。但随着岸滩初始坡度变为=1:15时, 岸滩横向冲淤规律发生了明显变化, 尽管波浪作用初期前滩仍会出现部分侵蚀(<20 min), 但随着波浪持续作用, 前滩内部冲淤情况发生明显变化, 逐渐由前滩侵蚀泥沙流失转变为内破碎区侵蚀并向冲泻区淤进, 该冲淤关系变化主要发生于前滩内部, 尽管与前文缓坡岸滩工况相同, 破碎点前内破碎区仍会出现明显冲刷坑, 但与前文缓坡岸滩工况不同的是冲刷坑侵蚀泥沙并未离岸堆积形成沙坝, 而是向岸淤进, 且随着波浪持续作用, 逐渐形成明显滩肩。由于泥沙在斜坡上的离岸输移会叠加重力分量作用, 而向岸输移需要克服重力分量作用, 因此向岸输移需要条件相对更苛刻。如图11b所示, 由于岸滩初始坡度较缓, 离岸重力分量较小, 且由于波周期较大, 而波高较小, 波陡很小, 更利于波浪适应更浅水深, 从而使更多能量用于前滩向岸输移, 这与自然界中长波向岸输沙理论相似。但对于图11a岸滩坡度较陡, 试验条件下, 由于重力分量较大, 仍以离岸输沙为主。

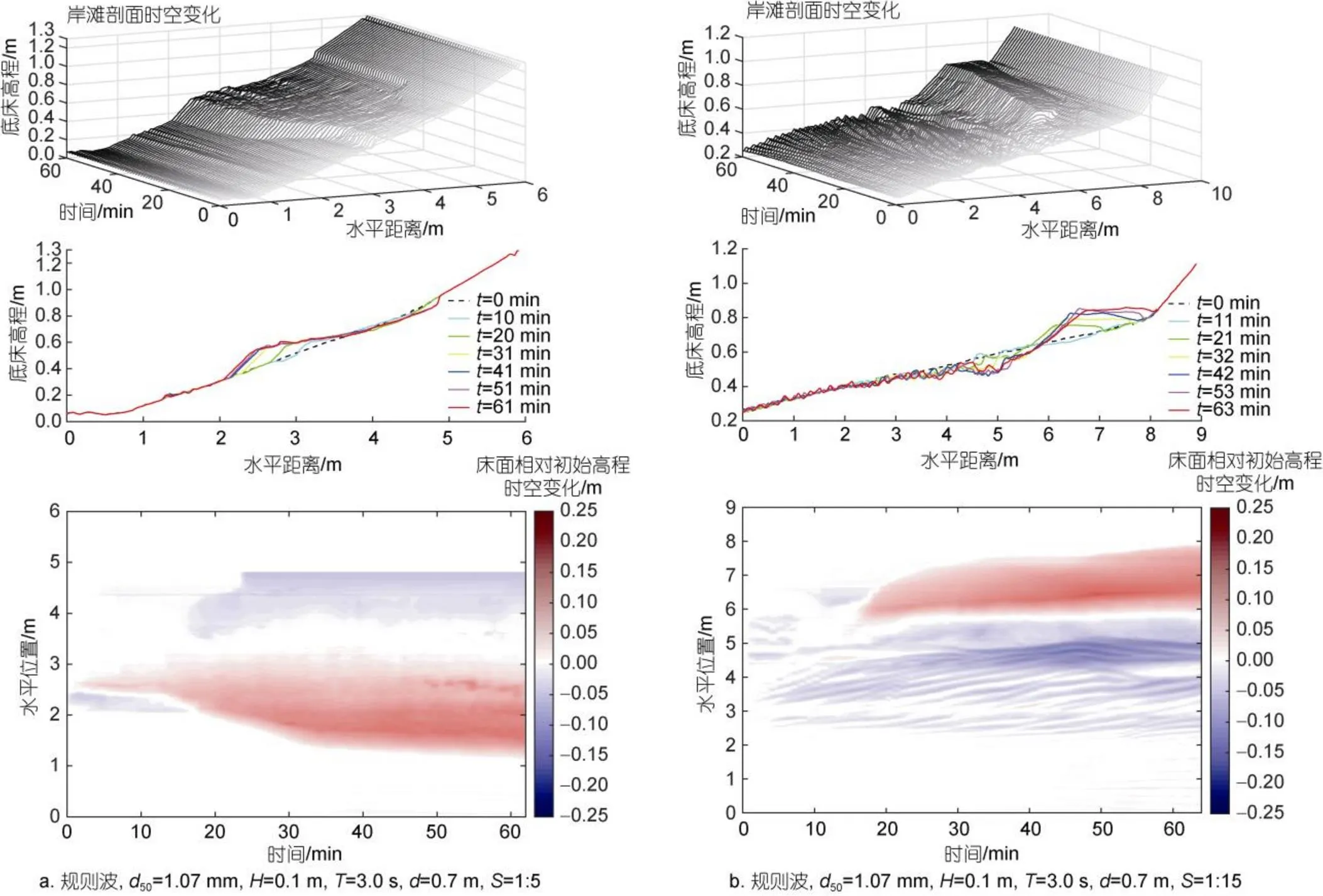
图11 长周期波况下不同初始坡度岸滩演变过程

3.4 风暴浪下岸滩演变过程

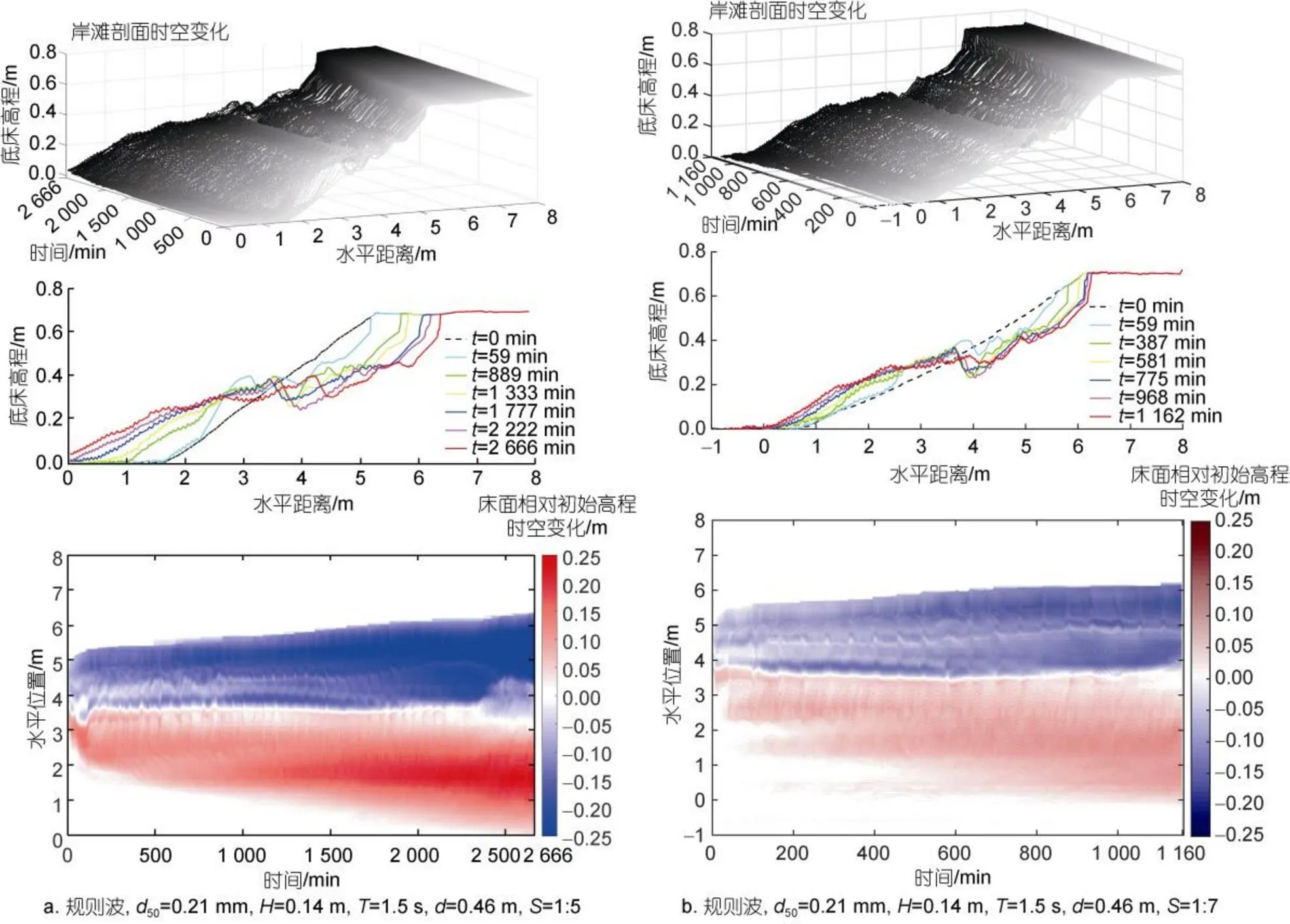
根据前文规则波作用下岸滩演变规律研究, 恒定入射波作用下, 岸滩冲淤呈单调变化, 随波浪持续作用, 不同初始坡度下通过前滩泥沙离岸堆积或离岸泥沙向岸淤积, 使得岸滩剖面不断调整, 随着岸滩坡度趋近于稳定坡度和离岸沙坝发育, 岸滩演变速度逐渐变缓, 岸滩稳定性不断提高, 直至岸滩达到相对稳定后呈动态平衡, 此过程中, 岸滩坡度对岸滩稳定性至关重要。但风暴潮期间, 波浪条件不断变化, 与规则波作用时岸滩稳定机制相差较大, 同时, 风暴增水也是导致岸滩原平衡被破坏、岸线快速蚀退的重要原因。为此, 本节将详细分析试验1中风暴浪工况中波高连续变化下岸滩剖面演变特征。根据前文规则波研究, 当岸滩坡度<1:10时, 岸滩稳定性较好, 为研究风暴对岸滩稳定性的侵蚀破坏机制, 试验选用了岸滩初始坡度=1:5和=1:15进行对比试验, 如图12所示。本研究风暴浪过程大致可以分为三个阶段: 动力增强阶段、极值稳定阶段和动力减弱阶段, 由于岸滩初始坡度=1:5时对造波机二次反射影响较大, 相同造波板冲程变化下, 实测波高变化明显弱于岸滩初始坡度=1:15。其中床面相对高程时空变化图中黑色线表征岸滩演变过程中沙坝实时位置变化。

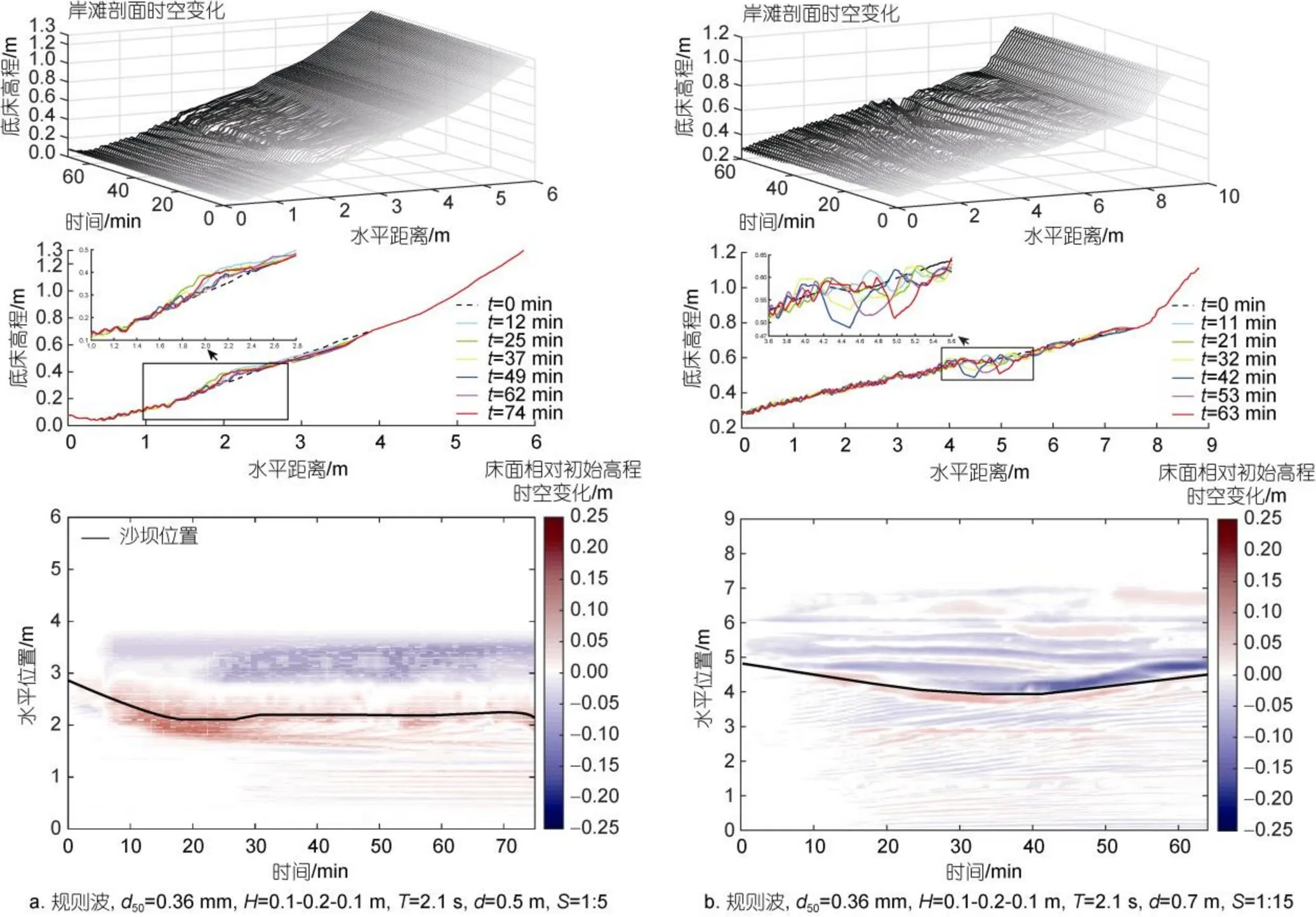
图12 波高连续变化下初始坡度S=1:15和S=1:15岸滩演变过程

与规则波相同, 初始坡度相差较大时, 岸滩横向冲淤关系存在明显差异, 而波高变化对岸滩横向冲淤关系影响很小。当岸滩初始坡度较缓时=1:15, 岸滩剖面变化主要集中在前滩区域, 而起坡点附近浅水区床面净冲淤变化较小, 主要表现为较长区域沙纹形成和变化。而前滩横向冲淤更为明显, 沙坝和坝前冲刷坑的位置随波高变化向离岸运动, 但由于作用时间较短, 沙坝未得到最够时间发育, 沙坝形态并不明显。结合床面相对初始高程时空变化图可见, 沙坝位置与波高变化呈明显响应关系, 波高增大时, 由于破碎点不断提前, 沙坝离岸运动, 而极值稳定阶段波高达到最大后, 沙坝快速发育并趋于稳定, 沙坝位置变化并不明显, 但当动力减弱阶段波高逐渐减小, 沙坝又随破碎点向岸迁移。相较于破碎区剖面变化, 整个风暴浪过程对冲泻区和岸线影响较小, 冲泻区侵蚀以及岸线蚀退主要发生在动力增强阶段的前半程, 在=10 min以后尽管波高仍在持续升高, 得益于沙坝的保护作用, 岸线侵退速度明显减缓, 且随着前滩剖面的调整, 岸滩稳定性也明显提高, 尽管>20 min后波高达到最大并持续作用, 但此过程中冲泻区侵蚀和岸线蚀退并不明显, 甚至在静水面与岸滩交界点附近(=6～7 m)出现明显淤积, 且动力递减阶段波高较小时, 岸滩淤积更为明显。而当岸滩初始坡度较陡时=1:5, 同样出现了前文规则波演变特征, 冲泻区明显侵蚀, 侵蚀泥沙离岸堆积形成沙坝, 岸滩整体坡度趋缓, 但由于前滩泥沙供给关系差异(Wang, 2020), 波高变化对前滩横向冲淤关系影响更小, 沙坝变化与波高并无明显响应关系。从上述地形变化与前文规则波研究基本一致, 由于岸滩初始坡度=1:15时岸滩稳定性较好, 本试验造波条件下, 仅波浪变化对岸滩整体危害有限, 主要集中于前滩区域, 表现在破碎点向离岸变化过程中沙坝位置以及破碎区和冲泻区之间横向冲淤变化。

4 讨论

根据前文规则波工况研究中不同波浪要素对岸滩影响特征, 试验条件下, 由于波浪周期限制, 试验波浪多为短波, 对岸滩影响程度与波浪强度正相关, 且已有研究也表明能量模型被应更适用于岸滩剖面的演变相关模拟(De Jesus Mariño Tapia, 2003; Masselink等, 2006)。根据微幅波理论下波能流计算公式为

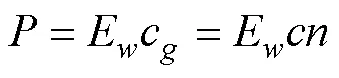
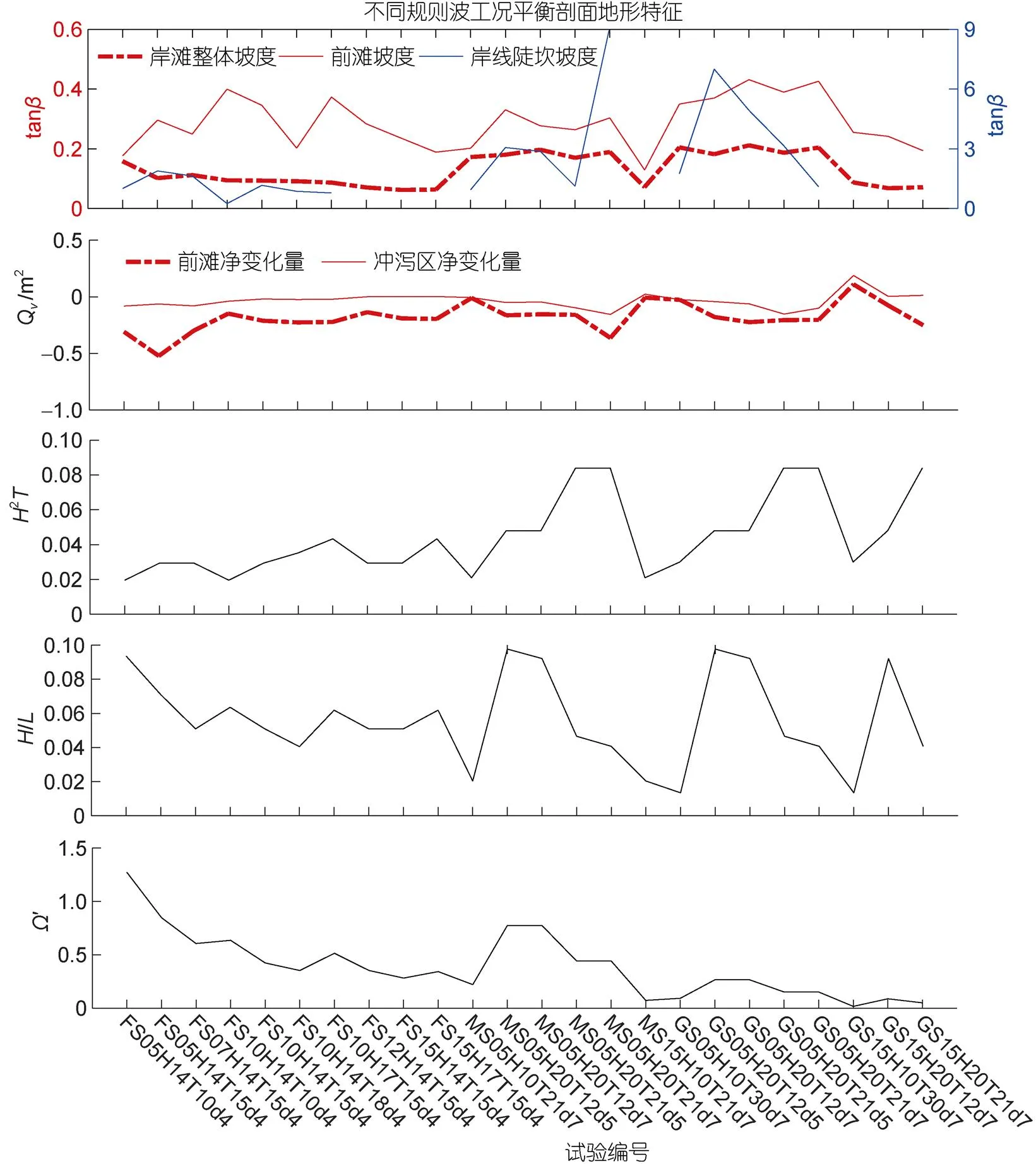
图13 不同工况下岸滩稳定坡度、前滩冲淤与波参数数特征、类Dean参数Ω′的关系

注: G代表粗砂50=1.07 mm、M代表中砂50=0.36 mm、F代表细砂50=0.21 mm; S05、S07、S10、S12、S15分别代表初始坡度=1:5、=1:7、=1:10、=1:12、=1:15岸滩; H10、H14、H17、H20分别代表波高=0.1 m、=0.14 m、=0.17 m、=0.2 m; T10、T12、T15、T18、T21、T30分别代表波周期=1.0 s、=1.2 s、=1.5 s、=1.8 s、=2.1 s、=3.0 s; d4、d5、d7分别代表试验水深=0.46 m、=0.5 m、=0.7 m。基于以上的工况注释, FS05H14T10d4代表工况为: F细砂50=0.21 mm, 岸滩初始坡度=1:5, 波高=0.14 m, 波周期=1.0 s, 试验水深=0.46 m

5 结论

中华人民共和国自然资源部, 2003～2021. 2002～2020年中国海洋灾害公报[M]. 北京: 自然资源部.

李明杰, 吴少华, 刘秋兴, 等, 2015. 风暴潮､大潮对广西涠洲岛西南沙滩侵蚀的影响分析[J]. 海洋学报, 37(9): 126-137.

蒋昌波, 伍志元, 陈杰, 等, 2014. 风暴潮作用下泥沙运动和岸滩演变研究综述[J]. 长沙理工大学学报(自然科学版), 11(1): 1-9.

蒋昌波, 伍志元, 陈杰, 等, 2015. 波浪动力因素变化对沙质岸滩演变的影响[J]. 海洋学报, 37(3): 106-113.

蒋昌波, 黄琼, 伍志元, 等, 2017. 沙质岸滩形态对海平面变化响应的数值研究[J]. 水动力学研究与进展, 32A(1): 81-87.

ATKINSON A, BALDOCK T E, 2016. A high-resolution sub-aerial and sub-aqueous laser based laboratory beach profile measurement system [J]. Coastal Engineering, 107: 28-33.

BALDOCK T E, ALSINA J A, CACERES I,, 2011. Large-scale experiments on beach profile evolution and surf and swash zone sediment transport induced by long waves, wave groups and random waves [J]. Coastal Engineering, 58(2): 214-227.

BALDOCK T E, MANOONVORAVONG P, PHAM K S, 2010. Sediment transport and beach morphodynamics induced by free long waves, bound long waves and wave groups [J]. Coastal Engineering, 57(10): 898-916.

CHARDÓN-MALDONADO P, PINTADO-PATIÑO J C, PULEO J A, 2016. Advances in swash-zone research: Small-scale hydrodynamic and sediment transport processes [J]. Coastal Engineering, 115: 8-25.

DE JESUS MARIÑO TAPIA I, 2003. Cross-shore sediment transport processes on natural beaches and their relation to sand bar migration patterns [D]. Plymouth: University of Plymouth: 305.

DEAN R G, 1977. Equilibrium beach profiles: US Atlantic and gulf coasts, ocean engineering report, No. 12 [R]. Newark: University of Delaware.

DEAN R G, 1991. Equilibrium beach profiles: characteristics and applications [J]. Journal of Coastal Research, 7(1): 53-84.

HATTORI M, KAWAMATA R, 1980. Onshore-offshore transport and beach profile change [J]. Coastal Engineering Proceedings, 1(17): 71.

KARUNARATHNA H, PENDER D, RANASINGHE R,, 2014. The effects of storm clustering on beach profile variability [J]. Marine Geology, 348: 103-112.

LARSON M, KRAUS N C, 1995. Prediction of cross-shore sediment transport at different spatial and temporal scales [J]. Marine Geology, 126(1/2/3/4): 111-127.

MASSELINK G, RUSSELL P, 2006. Flow velocities, sediment transport and morphological change in the swash zone of two contrasting beaches [J]. Marine Geology, 227(3/4): 227-240.

PULEO J A, LANCKRIET T, CONLEY D,, 2016. Sediment transport partitioning in the swash zone of a large-scale laboratory beach [J]. Coastal Engineering, 113: 73-87.

SEYMOUR R, GUZA R T, O'REILLY W,, 2005. Rapid erosion of a small southern California beach fill [J]. Coastal Engineering, 52(2): 151-158.

TÜRKER U, KABDAŞLI M S, 2006. The effects of sediment characteristics and wave height on shape-parameter for representing equilibrium beach profiles [J]. Ocean Engineering, 33(2): 281-291.

WANG J, YOU Z J, LIANG B C, 2020. Laboratory investigation of coastal beach erosion processes under storm waves of slowly varying height [J]. Marine Geology, 430: 106321.

YOU Z J, 2008. A close approximation of wave dispersion relation for direct calculation of wavelength in any coastal water depth [J]. Applied Ocean Research, 30(2): 113-119.

LABORATORY SIMULATION ON SANDY BEACH STABILITY UNDER STORM WAVE

WANG Jun1, YOU Zai-Jin1, LIANG Bing-Chen2

(1. Centre for Ports and Maritime Safety, Dalian Maritime University, Dalian 116026, China; 2. Shandong Provincial Key Laboratory of Ocean Engineering, Ocean University of China, Qingdao 266100, China)

In recent years, marine disasters such as storm surges have become more and more frequent with increasing problem of sandy coast erosion. Therefore, the stability and protection of beach is an urgent task. To study the stability mechanism of sandy beach under storm wave action, a series of flume tests were designed to observe, study, and analyze the stability mechanism and evolution process of sandy beach under storm wave action. In the experiments, images were taken and processed, from which the overall profile of the beach were real-time extracted dynamically according to the difference in pixel value between the water and the beach bed. The evolution process of sandy beach under different incident wave height, wave period, water depth, initial slope, and continuous change of wave height were compared and analyzed. The test results show that the stability of beach was directly related to the initial slope of beach and the development of sand bar, and the wave parameters mainly affected the disturbance amplitude of beach and the position change of sand bar and front beach erosion boundary. When the incident wave height changed continuously, the sand bar responded quickly and migrated offshore. An obvious positive correlation was found between the variation scale of the beach and the incident wave energy flow. The greater the wave energy flow, the greater the harm to the stability of the beach. The rising water level could increase the risk of coastal erosion in the foreshore. In addition, under the scale of this experiment, the foreshore was dominated by erosion. When initial slope of the beach was below the stable slope and the wave steepness was small, that is, the Dean parameter′ is small, obvious foreshore deposition would occur on the beach. This is very important for the study of beach restoration conditions at the experimental scale. Specifically, when the overall slope of the beach is 1:10 and the slope of the foreshore reaches 1:5～1:2.5, the stability of the beach is the best, the shape of the beach is the closest to the final equilibrium profile, and the time for the beach to stabilize is the shortest.

sandy beach; flume test; initial slope; wave parameters; stability; evolution; image processing

* NSFC-山东联合重点基金, U1806227号; 国家自然科学基金项目, 51739010号, 52001292号。王 俊, 博士后, E-mail: wangjun2021@dlmu.edu.cn

尤再进, 博士生导师, 教授, E-mail: b.you@dlmu.edu.cn

2022-01-28,

2022-04-13

P642

10.11693/hyhz20220100026