无限水深下波浪与二维水面物体作用的简单格林函数方法*

滕 斌 于 梅

无限水深下波浪与二维水面物体作用的简单格林函数方法*

滕 斌 于 梅

(大连理工大学海岸和近海工程国家重点实验室 辽宁大连 116024)

针对无限水深下波浪与二维水面物体相互作用问题, 传统的波浪格林函数形式复杂、计算缓慢, 为了提高计算效率和计算精度, 将流域分为物体周围的内域及远离物体的外域, 内域采用简单格林函数法, 外域采用多极子展开方法, 通过内外域边界匹配, 耦合求解得到流域中任意一点的速度势, 并可计算物体在波浪作用下的波浪激振力、附加质量、辐射阻尼及透射和反射系数。应用该方法计算了二维水面漂浮半圆和水面漂浮方箱的算例, 数值计算结果表明, 该方法可以方便、准确、快速地计算无限水深下波浪与任意漂浮物体的作用问题。

无限水深; 边界元方法; 简单格林函数; 多极子展开

近年来, 深海开发已进入千米甚至万米水深的时代, 对海上平台等大型漂浮结构设计和防护提出了更高的安全性要求, 对水动力分析计算提出了新的问题。对于波浪与结构物相互作用的水动力分析问题, 常采用基于格林函数的边界元方法进行求解。其格林函数又可分为简单格林函数, 满足波动条件的频域格林函数和时域格林函数。基于满足自由水面条件和远场条件波动格林函数的边界元方法, 一般只需在物面上剖分网格、布置未知量, 所建立的积分方程尺度较小, 但格林函数的快速和精确计算是该方法的难题。Liapis等(1985), Newman (1985a, 1985b), Magee等(1989), Lin等(1991), 黄德波(1992), 韩凌(2005)采用分区计算和拟合方法进行计算; Clément (1989a, 1989b), Duan等(2001), Chuang等(2007), Das等(2010)等通过问题转化, 采用常微分方程方法计算格林函数; Linton (1999), Rahman (2001)等则推导了格林函数新的解析表达式以加快计算, Huang等(2022)采用机器学习方法近似计算水面格林函数。但无论采用哪种方法, 波动格林函数都存在表达式冗长、编程难度大、计算费时和精度有限的问题。另外, 基于波动格林函数的边界元方法虽只需在物面上建立方程, 但若将方程拆分为齐次部分和非齐次部分, 会发现齐次部分的积分方程形式与物体内部的齐次Dirichlet边值问题对应的积分方程完全一致。对于后者, 我们知道, 在通常频率下, 齐次边值只有零解, 但在特征频率下, 我们所求的边界问题中也存在着非零解, 因此, 对应的积分方程也将出现解的不唯一性现象, 而这些不唯一解对应的特征频率通常被称为“不规则频率”, 因而会给出错误的计算结果。

当采用简单格林函数时, 需将流域分解为内域和外域两个部分(贺五洲等, 1992), 在内域上采用简单格林函数建立积分方程, 外域采用速度势的特征展开式做级数展开, 最后通过内外域交界面上压强和速度连续条件联立求解。该方法中的格林函数计算简便, 但需同时在物面、水面和内外域交界面上剖分网格、布置未知量, 离散的线性方程组较大。对于一般的二维问题, 目前的计算机足以满足其对计算量和存储量的需求。另外, 该方法外部问题与内部问题不使用同一套积分方程, 因而不存在“不规则频率”问题, 在各种计算条件下, 该方法构造的积分方程均可得到唯一的正确解。因此, 采用简单格林函数法求解波浪与二维物体作用问题是一个不错的选择。

对于水深中波浪与物体的相互作用问题, 外域速度势可采用特征函数展开方法进行构造, 特征值为色散关系2=-tan()的一个虚根和无穷多个实根, 其中为波浪频率,为波数,为重力加速度。当内、外域分界面远离物体时, 速度势的特征展开式只需取少量几项即可得到精确的结果。但随着水深的增加, 或波浪频率的增大, 非传播模态波数(实根)变得非常接近而成连续状态, 因而速度势特征展开式趋向于从零到无穷的连续函数, 这样需选取非常大的内部区域和较多的特征展开项数才能得到精确的结果, 使得计算效率和精度快速下降。而多极子展开方法采用球坐标系下的勒让德函数级数形式, 且只需取特征展开的少量项而具有收敛快速、计算精确的特点, 因此, 本文在外域采用多极子展开方法来求解无限水深下波浪对水面二维物体的作用问题。

1 数学模型和数值计算方法

1.1 问题的数学模型

考虑波浪与无限水深中水面漂浮物体的作用问题。假设波浪从物体的左侧入射, 入射波浪频率为, 物体受到简谐波浪的作用后发生同频率的简谐运动, 由于物体的运动在流域中产生辐射波浪。按物体运动广义自由度将物体运动的三个方向分解为水平振荡、垂向振荡和绕原点的转动。取二维笛卡儿直角坐标系,轴垂直向上,平面位于未扰动的静水面上, 原点位于静水面与物体交界的中心处, 如图1所示。将流域分为内、外流域, 分界面为图1所示半径为J的半圆面。

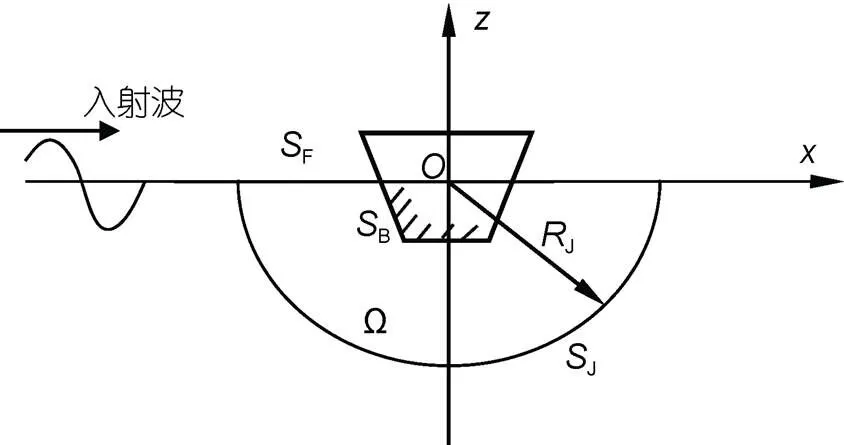
图1 波浪与无限水深中浮体的作用及流域分区示意图

注:F: 自由水面;B: 物体表面;J: 内外域分界面; Ω: 内域;J: 半径;表示笛卡尔直角坐标系

在不可压缩理想流体无粘无旋的假设下, 速度势满足Laplace方程

对于波浪与浮体的相互作用问题, 由于问题是线性的,等物理量都是频率为的简谐函数, 这样, 我们可分离出时间因子e–iωt, 将速度势做如下分解,

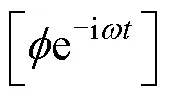
(1) 自由水面条件

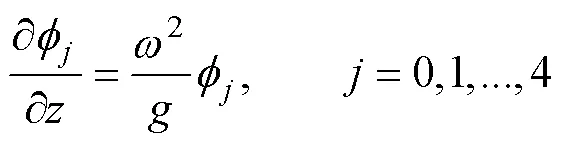
式中,为重力加速度。

(2) 物面条件

(3) 深水条件

1.2 积分方程和水面多极子展开

将物面和水面边界条件代入式(8), 得

在外部流域, 采用多极展开法将速度势展开成水面点源、反对称偶极子和远场无波势的线性叠加形式

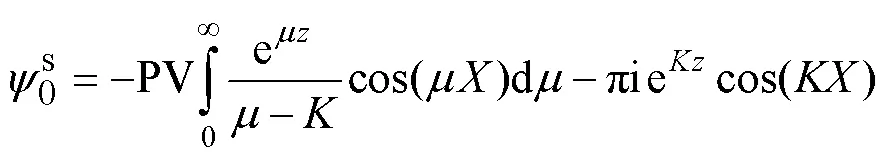
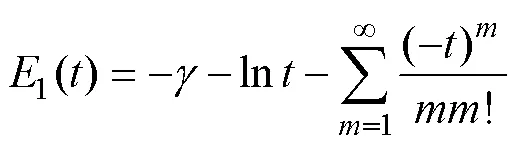
在远场, 点源势可近似为

式中,为漂浮物体半径。

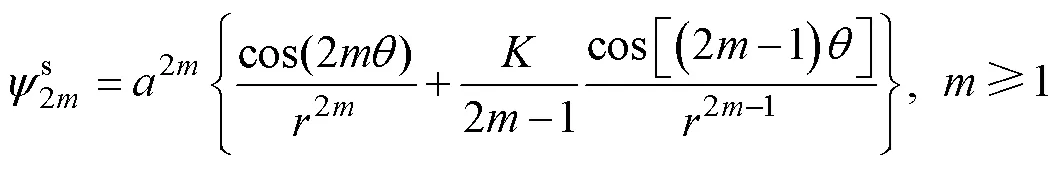
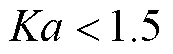
1.3 匹配边界元法的数值实现

将物面离散成B个单元, 水面离散成F个单元, 内外域交界面上离散成J个单元。采用坐标变换, 将每个单元变换到(-1, 1)的局部坐标系下, 再在单元内引入形状函数, 则单元内的坐标和速度势可写为

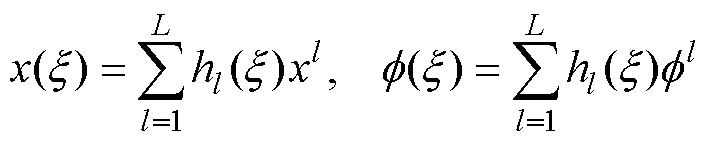
线积分微长度为

将式(20)和式(21)代入方程(19a)和(19b), 得

整理后可得线性方程组

1.4 波浪力、水动力系数和波高

求得了物面和水面节点处的速度势后, 物体上的波浪作用力可通过物面上的压强积分求得,物体上、方向作用力及绕原点的波浪作用力矩为

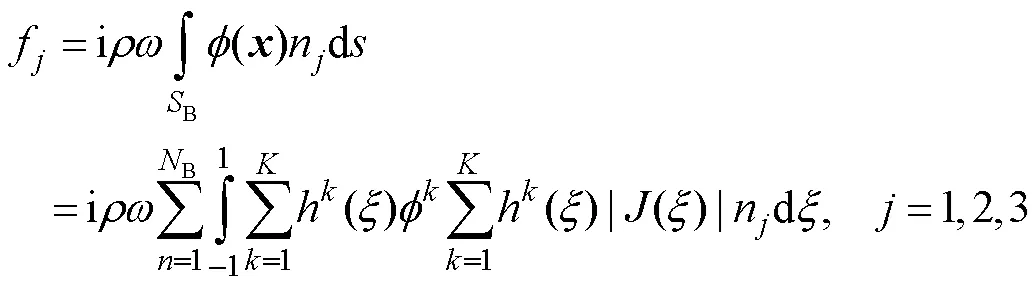
同样, 可求得附加质量和辐射阻尼为

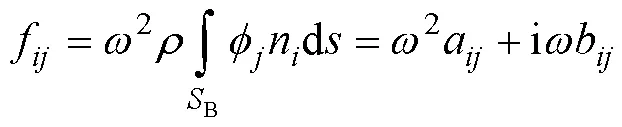
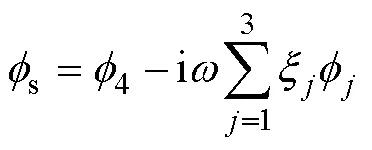
考虑到远场无波势在远场衰减为零, 远场散射势可简化为

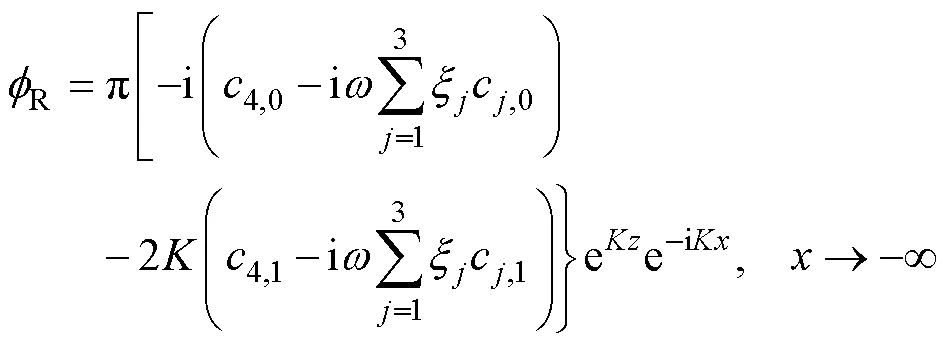
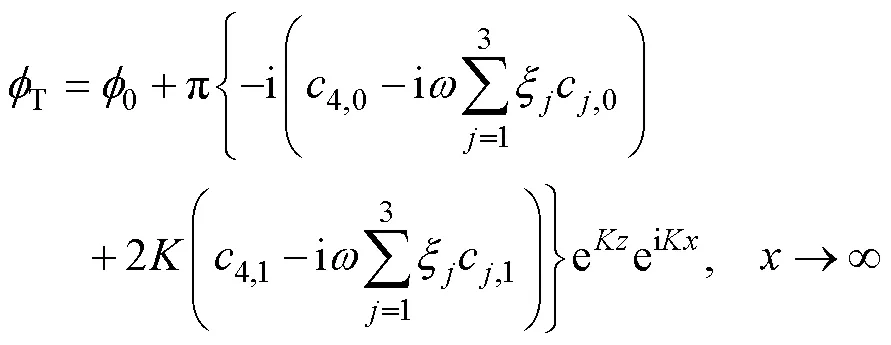
透射波浪高度为

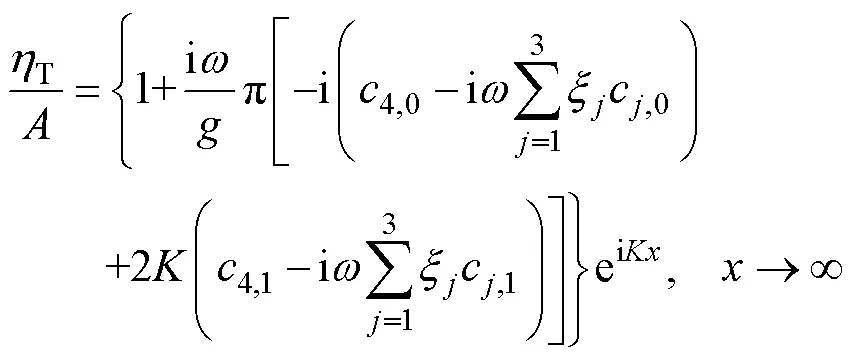
2 数值算例

图2给出了水面固定半圆算例通过两种方法计算得到的激振力结果的对比。“RkGreen”表示本文采用的简单格林函数方法, “FsGreen”表示波动格林函数法(下同)。可以看出, 两种方法计算的结果吻合很好, 但波动格林函数法的计算结果在某些频率处出现骤然跳跃,即出现了前面所述的“不规则频率”问题,这些“不规则频率”的产生是由于求解积分方程的方法导致的, 并非物理上真正存在着“不规则频率”。而本文方法在整个计算域内都得到了准确的结果。

图3是水面固定半圆反射系数和透射系数随波数的变化曲线。由曲线可以看出, 两种计算方法的结果均呈现出低频区波浪的反射系数较小, 高频区较大; 而波浪的透射系数在低频区较大, 高频区较小, 且一直满足反射系数和透射系数平方和为1的关系。而波动格林函数法仍存在“不规则频率”问题, 简单格林函数算法由于其积分方程解的唯一性便可以很好地解决这一问题。

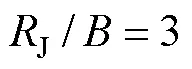
图2 简单格林函数边界元与波动格林函数边界元求解水面固定半圆激振力对比

图3 简单格林函数边界元与波动格林函数边界元求解透射反射系数对比

注: RkGreen表示简单格林函数法, FsGreen表示波动格林函数法; 横坐标是深水波数和半圆半径的乘积

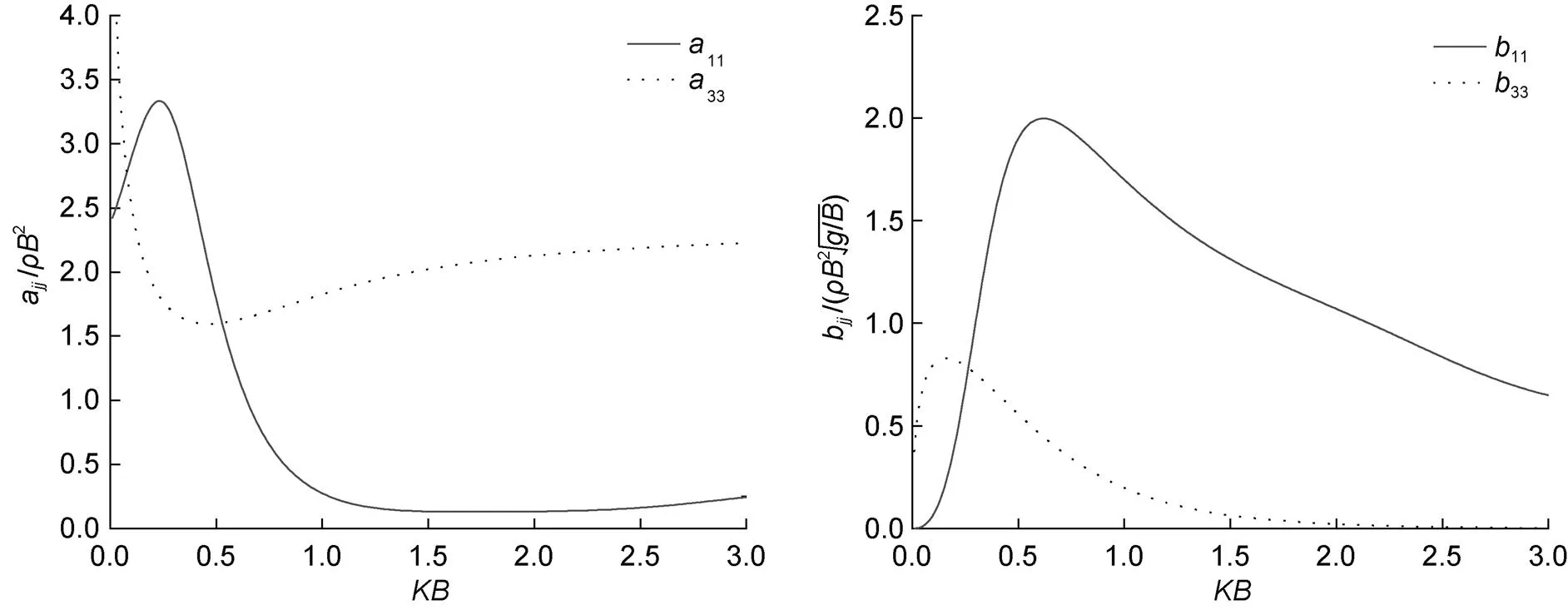
图4 水面方箱附加质量及辐射阻尼随波数的变化曲线

3 结论

对于波浪与无限水深中水面二维浮体作用问题, 采用简单格林函数和Ursell (1950)提出的水面多极展开表达式, 建立了边界元法与多极展开耦合求解的计算方法。该方法只需取少量的多极展开项数, 应用指数积分计算求解, 避免了水面格林函数的复杂计算问题, 具有算法简单, 计算准确、快速, 且可避免“不规则频率”干扰的特点。应用该方法计算了无穷水深中水面方箱的绕射和辐射问题, 求得了水面方箱的附加质量、辐射阻尼和波浪激振力随波数的变化函数。结果表明: 垂荡附加质量在零频率处趋于无穷, 高频处趋于有限值; 纵荡附加质量在零频率处为有限值, 高频处趋于有限值。垂荡和纵荡辐射阻尼在零频处为零, 高频处趋于零。

图5 水面方箱上波浪激振力随波数的变化曲线

贺五洲, 戴遗山, 1992. 求解零航速物体水动力的简单Green函数方法[J]. 水动力学研究与进展A辑, 7(4): 449-456.

黄德波, 1992. 时域GREEN函数及其导数的数值计算[J]. 中国造船(4): 16-25.

韩凌, 2005. 应用时域格林函数方法模拟有限水深中波浪对结构物的作用[D]. 大连: 大连理工大学: 83-88.

ABRAMOWITZ M, STEGUN I A, 1972. Handbook of mathematical functions with formulas. Graphs, and mathematical tables [R]. Washington: National Bureau of Standards (DOC): 229.

CHUANG J M, QIU W, PENG H, 2007. On the evaluation of time-domain Green function [J]. Ocean Engineering, 34(7): 962-969.

CLÉMENT A H, 1998a. An ordinary differential equation for the Green function of time-domain free-surface hydrodynamics [J]. Journal of Engineering Mathematics, 33(2): 201-217.

CLÉMENT A H, 1998b. Recent developments of computational time-domain hydrodynamics based on a differential approach of the green function [C] // Proceedings of the EUROMECH-374. Poitiers: 105-114.

DAS D, MANDAL B N, 2010. Construction of wave-free potential in the linearized theory of water waves [J]. Journal of Marine Science and Application, 9(4): 347-354.

DUAN W Y, DAI Y S, 2001. New derivation of ordinary differential equations for transient free-surface Green functions [J]. China Ocean Engineering, 15(4): 499-507.

HUANG S, ZHU R C, CHANG H Y,, 2022. Machine learning to approximate free-surface Green’s function and its application in wave-body interactions [J]. Engineering Analysis with Boundary Elements, 134: 35-48.

LIAPIS S, BECK R F, 1985. Seakeeping computations using time-domain analysis [C] // Proceedings of the 4th International Conference on Numerical Ship Hydrodynamics. Washington: National Academy of Sciences: 34-56.

LIN W M, YUE D, 1991. Numerical solutions for large-amplitude ship motions in the time domain [C] // Proceedings of the 18th Symposium on Naval Hydrodynamics. Washington, DC: National Academy Press: 41-66.

LINTON C M, 1999. Rapidly convergent representations for Green’s functions for Laplace’s equation [J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 455(1985): 1767-1797.

LIU Y Y, GOU Y, TENG B,, 2016. An extremely efficient boundary element method for wave interaction with long cylindrical structures based on free-surface Green’s function [J]. Computation, 4(3): 36.

MAGEE A, BECK R F, 1989. Vectorized computations of the time-domain green function [C] // Fourth International Workshop on Water Waves and Floating Bodies. Hardangerfjord Hotel, Oystese, Norway.

NEWMAN J N, 1985a. Algorithms for the free-surface Green function [J]. Journal of Engineering Mathematics, 19(1): 57-67.

NEWMAN J N, 1985b. The evaluation of free-surface Green functions [C] // Proceedings of the 4th International Conference on Numerical Ship Hydrodynamics. Washington.

RAHMAN M, 2001. Simulation of diffraction of ocean waves by a submerged sphere in finite depth [J]. Applied Ocean Research, 23(6): 305-317.

TAYLOR R E, HU C S, 1991. Multipole expansions for wave diffraction and radiation in deep water [J]. Ocean Engineering, 18(3): 191-224.

URSELL F, 1949. On the heaving motion of a circular cylinder on the surface of a fluid [J]. The Quarterly Journal of Mechanics and Applied Mathematics, 2(2): 218-231.

URSELL F, 1950. Surface waves on deep water in the presence of a submerged circular cylinder. I [J]. Mathematical Proceedings of the Cambridge Philosophical Society, 46(1): 141-152.

YU Y S, URSELL F, 1961. Surface waves generated by an oscillating circular cylinder onwater of finite depth:theory and experiment. Journal of Fluid Mechanics 11, 529–551. Mathematical Proceedings of the Cambridge Philosophical Society, 46(1): 141-152.

A BEM WITH SIMPLE GREEN'S FUNCTION FOR WAVE INTERACTION WITH A 2D BODY AT THE SURFACE OF INFINITE WATER

TENG Bin YU Mei

(Dalian University of Technology, State Key Laboratory of Coastal and Offshore Engineering, Dalian 116024, China)

To understand the interaction of waves with a two-dimensional surface body in infinite water depth, the traditional wave Green’s function has complex form and slow calculation. In order to improve the calculation efficiency and accuracy, the watershed was divided into inner domain around the object and outer domain far away from the object. Simple Green’s function method was adopted in the inner domain, and multi-pole expansion method was adopted in the outer domain. The velocity potential of any point in the watershed can be obtained through coupling solution by matching inner and outer domain boundaries. The wave excitation force, additional mass, radiation damping and transmission and reflection coefficients of the object under wave action can also be calculated. The method was applied to calculate two-dimensional water surface floating semicircle and water surface floating square box, and the numerical results show that the method can conveniently, accurately and quickly calculate the interaction between waves and arbitrary floating objects in infinite water depth.

infinite water depth; boundary element method (BEM); simple Green’s function; multipole expansion

* 国家重点研发计划项目, 2021YFB2601100号。滕 斌, 博士生导师, 教授, E-mail: bteng@dlut.edu.cn

2021-12-10,

2022-02-24

TV139.2

10.11693/hyhz20211200318