珠江流域下游近60年输沙率年际与年内变化特征

杨远东, 王永红, 蔡斯龙, 刘 锋, 杨清书

(1.中国海洋大学 海洋地球科学学院 海底科学与探测技术教育部重点实验室,山东 青岛 266100; 2.广东省水文局, 广州 510150; 3.中山大学 海洋科学学院, 广州 510275)

河流入海水沙是三角洲的物质基础[1]，河流通过向海洋输送陆源物质从而影响河口、海岸及边缘海，河流的输送量占全球陆—海沉积物通量的95%[2]，近年来，随着人类活动的加剧，全球各主要河流输沙率均发生巨大的变化，Milliman[3]指出在过去50 a来欧洲众多河流入海泥沙通量发生了明显的下降。Meade等[4]对Mississippi河研究发现，其输沙量在几十年间下降了75%；Loisel等[5]对湄公河进行研究，发现目前湄公河悬浮泥沙浓度(SSC)现在正在以每年5%的趋势减少。与国外河流相似，近几十年河流水沙异变在我国同样显著[6]，彭涛等[7]对长江干流寸滩、宜昌、汉口和大通4个控制站水沙进行研究，发现近60 a来长江干流4个站点径流量年际变化相对平稳，而输沙量年际变化较为剧烈，大多数站点水沙在1968年前后和21世纪初期发生了突变：府仁寿等[8]提出近几十年受气候变化和人类活动共同影响，长江流域输沙量大幅减少，由此导致了长江流域中下游严重的生态环境问题：张金萍等[9]对黄河三门峡水库入库潼关水文站1919—2015年共计97 a径流与输沙量数据进行研究，表明潼关水文站径流量与输沙量具有显著下降趋势，且在未来一段时间内这种变化趋势将持续。珠江作为我国南方地区的重要河流，其河口处的珠江三角洲由于独特的地理位置在中国经济发展中起着举足轻重的作用，近年来，珠江流域及三角洲地区受人类活动影响显著，各种研究也较多，但是对这一地区输沙率的历史变化研究较少，本文基于1960—2017年珠江流域下游主要水文站(西江高要、北江石角、东江博罗)年际及年内月度输沙率数据，运用多种方法分析珠江流域下游地区输沙率年际与年内变化特征，并分析人类活动对其造成的影响，以期为流域的综合治理提供参考。

1 研究区概况

珠江发源于云南省马雄山，由西江、北江与东江三大支流构成，地理坐标位为北纬21°31′—26°49′，东经102°14′—115°53′，全长2 400 km，流域面积45万km2，流经云南、贵州、广西、广东、湖南、江西6个省(区)和越南的北部，是中国第二大河，境内第三长河。珠江流域地处亚热带，北回归线横贯流域的中部，气候温和多雨，多年平均温度为14～22℃，多年平均降雨量1 200～2 200 mm，多年平均径流量3 100多亿m3(1954—2016年)，多年平均输沙率2 800多万t(1954—2016年)，径流水沙季节分配很不均匀，常年4—9月份洪水期多年平均径流量约占全年的80%，输沙率占91%～95%。

珠江流域西北两江分别在广东省三水市思贤滘东西两侧、东江在广东省东莞市石龙镇汇入珠江三角洲。高要(北纬23.02°, 东经112.27°)、石角(北纬23.11°，东经112.52°)、博罗(北纬23.11°，东经114.17°)分别为进入三角洲之前西、北、东江最主要的水文控制站(图1)。

图1 珠江流域及高要、石角、博罗水文站位置

2 数据来源与研究方法

2.1 数据来源

本文收集了珠江流域进入珠江三角洲之前西、北、东江的主要水文控制站——高要站、石角站、博罗站1960—2017年年度及月度输沙率数据，长时间序列输沙率数据来源于广东省水文局(历史测量数据)，中山大学(历史保存数据)与《中国河流泥沙公报》(2002—2017年)。珠江流域主要大坝建设数据来源于中国大坝工程学会网站。

2.2 研究方法

2.2.1 年际变化特征研究方法

(1) 输沙率年际变差系数(Sv)与输沙率年际极值比(Sw)。为研究输沙率的年际变化特征，与径流年际变化类似[径流年际变异性常用变差系数(Cv)与年际极值比(w)来表示]，引入输沙率变差系数(Sv)与输沙率年际极值比(Sw)，输沙率变差系数(Sv)用来说明水文变量长期变化的稳定程度，其值为输沙率样本序列的标准差与算术平均值的比值，Sv值越大，年输沙率的年际变化越大，可以作为反映输沙率年际变化不均匀性的重要指标。输沙率变差系数(Sv)计算公式如下:

(1)

式中:ki为模比系数,即第i年的年输沙率与平均年输沙率的比值;n为系列长度。

年际极值比(Sw)是指径流量变化的绝对值比例，其大小用多年最大(Wmax)、最小(Wmin)年输沙率比值表示，年际极值比计算公式如下：

Sw=Wmax/Wmin

(2)

(2) M-K趋势分析法与滑动平均法。M-K趋势分析法(Mann-Kendall法)是一种非参数统计检验方法，其优点是样本不需要遵循一定的分布，也不受少数异常值的干扰，更适用于类型变量与顺序变量，计算也比较简便，最初由曼和肯德尔提出原理并发展了这一方法。现已成为世界气象组织推荐并已广泛使用的非参数检验方法，适用于水文、气象等非正态分布的数据。其计算公式见公式(3)—(6)，设径流序列为x1，x2，…，xn；Sk表示第i个样本xi>xj(1≤j≤i)的累计数。

(3)

其中：

(4)

在时间序列随机独立的假设下，Sk的均值与方差分别为：

(5)

将Sk标准化为：

(6)

式中:UF1=0,给定显著性水平α,若|UF|>Uα,表明序列存在明显的趋势变化。将此方法引用到反序列,序列顺序变为xn,xn-1,…,x1,反序列标准化由UBk表示;UBk,UFk可组成两条曲线,在这里设定α值为0.05,临界值U0.05为±1.96。

滑动平均法因其简单直观性，在水文学研究中应用较为广泛。其主要思路是将时间序列x1，x2，…，xn的几个前期值和后期值取平均，求出新的序列yt。其计算公式如公式(7)[10]：

(7)

式中:yt为新序列;k为滑动平均尺度;xt+i为参与此次生成新序列的旧序列值;k=1时为3 a滑动平均值;k=2时为5 a滑动平均值;若Xn有趋势性,选择合适的k,即可通过将其趋势清晰地表示出来。

(3) 累积距平法。为了更直观地观察输沙率的年度变化特征，引入输沙率累计距平方法[11-12]，输沙率累积距平计算方法如下[13]：

(8)

2.2.2 年内变化特征研究方法

(1) 集中度与集中期法。目前对于长序列输沙率年内变化的分析方法较少，本文借鉴长序列径流年内分配的分析方法，对珠江三角洲西江高要站、北江石角站、东江博罗站近几十年输沙率的年内变化特征进行分析，具体原理与计算过程见文献[14]。计算公式如公式(9)—(11)：

(9)

RCPyear=arctan(Rx/Ry)

(10)

(11)

式中:RCDyear为年输沙率集中度;RCPyear为年输沙率集中期;Ryear为年输沙率;Rx,Ry分别为12个月的分量之和所构成的水平、垂直分量;ri为第i月的输沙率;θi为第i月输沙率的矢量角度。RCDyear越大表示输沙率越分散,越小输沙率越集中;RCPyear表示1年中最大输沙率出现的时间,表1为各个月份包含及代表角度值。

表1 RCPyear计算各月份包含及代表角度值

(2) 等值线图法。等值线图又称等量线图，是以相等数值点的连线表示连续分布且逐渐变化的数量特征的一种图型，具有更强的直观性。

3 结果与分析

3.1 数据分析

(1) 输沙率年际变差系数(Sv)与输沙率年际极值比(Sw)。珠江流域西、北、东江1960—2017年径流年际变化特征值计算结果见表2，西、北、东江输沙率变差系数(Sv)值在0.5左右，总体数值较大，说明珠江流域输沙率年际变率较大，输沙率稳定性较差，稳定性大小顺序为北江大于西江大于东江，西、北、东江输沙率变差系数(Sv)值与输沙率年际极值比(Sw)值变化趋势有所不同，输沙率年际极值比(Sw)值介于7.15～16.15，北江与西江Sw值较大且较为接近，说明北江与东江更易出现输沙率的极大值或极小值点，综合输沙率变差系数(Sv)值与输沙率年际极值比(Sw)值可以发现，东江为三江中输沙率变异性最大的支流。

表2 1960-2017年珠江流域西、北、东江输沙率年际变化特征

(2) M-K趋势分析法与滑动平均法。用于诊断连续水文序列趋势性方法较多，其中应用最广范、最为简便直观的方法为M-K趋势分析法与滑动平均法，本文分别用这两种方法对珠江流域西、北、东江1960—2017年输沙率趋势性进行分析。

由图2可知，高要、石角、博罗站历史输沙率变化幅度较大，西江、东江输沙率明显下降，通过M-K趋势检验法检测发现，西江高要站输沙率变化曲线UF与UB在2001年前后相交，交点位于0.05置信区间内，证明高要站输沙率在2001年开始出现下降趋势，UF在2004年之后始终位于0.05置信区间之外，输沙率持续下降。高要站2001—2016年平均输沙率仅为1970—2000年的30%，在流量基本保持稳定的情况下，反映了西江含沙量的快速下降；石角站2000年之后输沙率虽有下降，但下降趋势不明显，UF始终位于0.05置信区间之内，2001—2016年平均输沙率为1960—2000年的80%。东江博罗站自1987年前后开始下降，1990年之后UF始终位于0.05置信区间之外，下降趋势较明显，2001—2016年平均输沙率为1960—2000年的65%。

图2 1960-2017年高要、石角、博罗输沙率M-K检验

珠江流域高要、石角、博罗1960—2017年输沙率3 a滑动平均值与5 a滑动平均值见图3。可见，高要、石角、博罗水文站1960—2017年输沙率3 a滑动平均值与5 a滑动平均值较为相似，近几十年均呈现“上升—下降—上升”的波动过程，但3站输沙率总体呈下降趋势，尤其以西江高要站下降最为迅速，其次为东江博罗站，下降最缓慢的为北江石角站。对高要、石角、博罗1960—2017年输沙率数据作线性回归分析，研究其58 a间总体变化特征，线性回归方程见图3，高要、石角、博罗线性分析相关系数r值分别为0.33，0.04，0.34，由线性回归统计学可知，当α=0.05，n=58时，查表得相关系数r=0.259，3个流域中西江、东江|r|值大于r0.05，证明这两个支流输沙率下降趋势明显，北江|r|值小于r0.05，输沙率下降趋势不明显。综合图3逐年输沙率与3 a，5 a输沙率滑动平均值可知，西江高要站输沙率下降始于1997年前后，北江石角站下降趋势不明显，东江博罗站输沙率下降始于1984年前后。

综合比较滑动平均值(3 a，5 a)法与M-K趋势检验法，可以发现其反映的总体规律基本相似，两种方法都显示西江高要站与东江博罗站输沙率存在下降趋势，而北江石角站输沙率总体变化趋势不大。但其变化的时间存在差异，M-K趋势检验法检测西江高要站输沙率在2001年开始出现下降趋势，东江博罗站自1987年前后开始下降，这分别比滑动平均值法迟3～4 a，其主要原因是由于滑动平均法只是将3 a或5 a进行滑动平均，使曲线变得平缓，但并不能避免下降过程中会出现小的波动，从这一方面来说，M-K趋势在统计学上讲意义更大，同时滑动平均值法可以起到很好的检验作用，综合分析两种结果，认为1960—2017年珠江三角洲顶点处西江、东江输沙率下降趋势显著，起开始下降年份分别为2001年、1987年，北江下降趋势不明显。

图3 1960-2017高要、石角、博罗年输沙率及3 a，5 a滑动平均值

(3) 累积距平法。高要、石角、博罗3站1960—2017年输沙率累计距平见图4，高要、博罗累积距平形状较为相似，都经历一个上升—下降过程，其上升、下降的转折点分别在1998年、1987年前后，而石角站累积距平曲线形状较为曲折，存在多个转折点。

(4) 集中度与集中期法。珠江流域高要、石角、博罗水文站1960—2017年10 a尺度的输沙率集中度与集中期计算结果见表3，由表3可知，输沙率的年内集中程度为西江高于北江高于东江，西江高要站年内输沙率集中度在1960—2009年较为稳定，基本维持在0.8左右，2010—2017年迅速减小为0.7，北江石角站年内输沙率集中度自1960年以来基本呈增大趋势，东江博罗站年内输沙率集中度自1960年以来基本呈减小趋势，其RCDyear值较西江高要站与北江石角站略小。

图4 1960-2017年高要、石角、博罗输沙率累积距平

表3 高要、石角、博罗水文站年输沙率集中度与集中期

根据年输沙率集中期对应的角度，可以发现西江高要站年内输沙率主要集中在7月份，但近几十年其输沙率集中度对应数值在缓慢变小，说明其最大输沙率对应的月份不变，但在最大输沙月内最大输沙日期向前移动；北江石角站输沙率集中期在5月、6月份交替出现，1970—1989年期间最大输沙发生在5月份，其余时间最大输沙发生在6月份，近几十年在季节尺度无明显向前或向后移动的趋势；东江博罗站输沙率集中期在6月、7月份交替出现，近几十年其输沙率集中度对应数值在缓慢变大，说明其最大输沙率对应的时间在向后移动，1960—1999年期间最大输沙基本发生在6月份，此后最大输沙多发生在7月份。

(5) 等值线图法。对1960—2017年高要、石角、博罗水文站月度输沙率作等值线图(图5)，从等值线图中可以清楚地看出输沙率年内的分散程度与最大、最小径流出现的时间。输沙率等值线图与输沙率集中度与集中期表格演变阶段具有一致性，等值线图中年内输沙率较分散年份，输沙率集中度往往也较低，反之亦然，而输沙率集中期角度的波动与等值线图最大值的上下移动也有很好的对应性。

图5 1960-2017年高要、石角、博罗输沙率等值线

3.2 输沙率年际与年内变化原因分析

3.2.1 输沙率年际变化原因分析 影响河流年际输沙率变化的原因众多，而珠江三角洲输沙率年际变化受人类活动影响程度较大[15-16]，对珠江流域西、北、东江径流量近几十年分析，发现其径流量并未发生较大变化[17]，因此造成输沙率剧烈变化的主要原因是河流含沙量的变化。

图6为高要、石角、博罗1960—2017年河流含沙量的变化图。由图6可知，近几十年西江高要站、东江博罗站河流含沙量呈下降趋势，且西江下降率高于东江，北江石角站含沙量变化不大，含沙量的变化趋势与输沙率变化趋势相一致，且变化时间也基本吻合，西江高要站含沙量在1997年开始下降，东江博罗站含沙量在1987年前后开始下降。

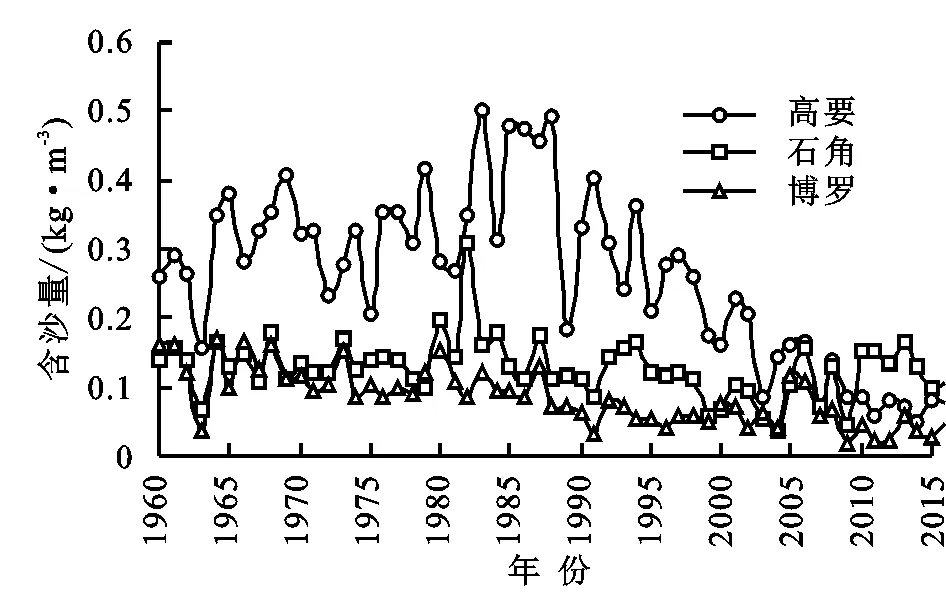
图6 1960-2017年高要、石角、博罗站含沙量变化

人类活动主要通过影响河流含沙量的变化从而影响流域的输沙率，通过对国内外人类活动对流域输沙率的干预状况研究发现，人类活动主要通过两种方式改变河流的含沙量，一是流域植被覆盖率的变化，植被覆盖率影响土壤侵蚀，从而对河流含沙量产生影响，而植被覆盖率与国家或地区有关的环境政策与流域的综合管理或治理情况有关；二是流域大坝、水库的修建，大坝、水库在完成其蓄水的同时，也使大量的泥沙在大坝前或水库中积聚，从而改变下游地区的含沙量。

据珠江水利委员会水农处通过遥感资料统计，1984—1988年相比1954年，水土流失土地的面积增大了38.9%，从而使大量泥沙下泄，增大了河流的含沙量，这与图5对应较好，由于西江来沙量占珠江流域总的来沙量的绝大部分，在这两个时间点其变化特征也最大，北江偏小，东江虽呈现下降趋势，但由于其输沙量在珠江流域所占比例较小，不影响总体的变化。1982年全国第4次水土保持工作会议以后，水土保持治理工作逐渐开展，这是珠江流域含沙量下降的一个原因。

但随着新建大坝、水库数量及库容量的增大，这些大工程也越来越成为影响流域河流含沙量的一个重要因素[18]，本文统计了珠江流域较大规模大坝、水库的修建情况，包括大坝、水库的库容及建成时间，具体数据见表4。西江流域较大的水利工程一般在1997年之后，1997年建成的天胜桥水电站其库容量高于前期建成的较大规模的水库库容量之和，而2006年建成的龙滩水电站，是当今珠江流域最大的水利工程，同时也是继三峡水电站之后国内第二大水电站，其库容量高达273亿m3，对于泥沙的积聚作用巨大[18]。由图5可以看出，含沙量在这两个时间节点都有明显的下降过程，可见大坝、水库的修建对于含沙量的减小具有明显的作用。北江水电站规模较小，且修建时间较早，大坝修建引起的含沙量的降低与水土流失造成的含沙量的增大互相抵消一部分，导致含沙量变化不大，而东江1969年修建了新丰江水电站，库容量高达139亿m3，相比于东江较小的输沙率占比(图7)，其库容量相对较大，在1969年之后博罗站含沙量有一个下降过程，此后随着枫树坝与白盆珠水电站的建成，其含沙量又经历了一个下降过程。

3.2.2 输沙率年内变化原因分析 珠江流域高要、石角、博罗输沙率年内变化主要与两个因素有关，一是径流的年内分配，二是年内河流含沙量的变化。通过对比高要、石角、博罗1960—2017年径流年内集中度与集中期[17]，发现高要站输沙率集中度与径流集中度变化特征相似，两者都表现为1960—2009年较为稳定，2010—2017年迅速减小，径流集中期与输沙率集中期基本相似，但输沙率集中度远远大于径流集中度，表现为输沙率年内更加集中，北江石角、东江博罗站输沙率集中度、集中期表现为与径流集中度、集中期密切相关。而分析河流年内含沙量分析，发现虽然整体含沙量呈下降趋势，但每个月相对全年所占比例变化不大，说明输沙率的年内变化主要与径流的年内变化有关，而径流的年内变化又与上文提到的大坝、水库的修建有关。

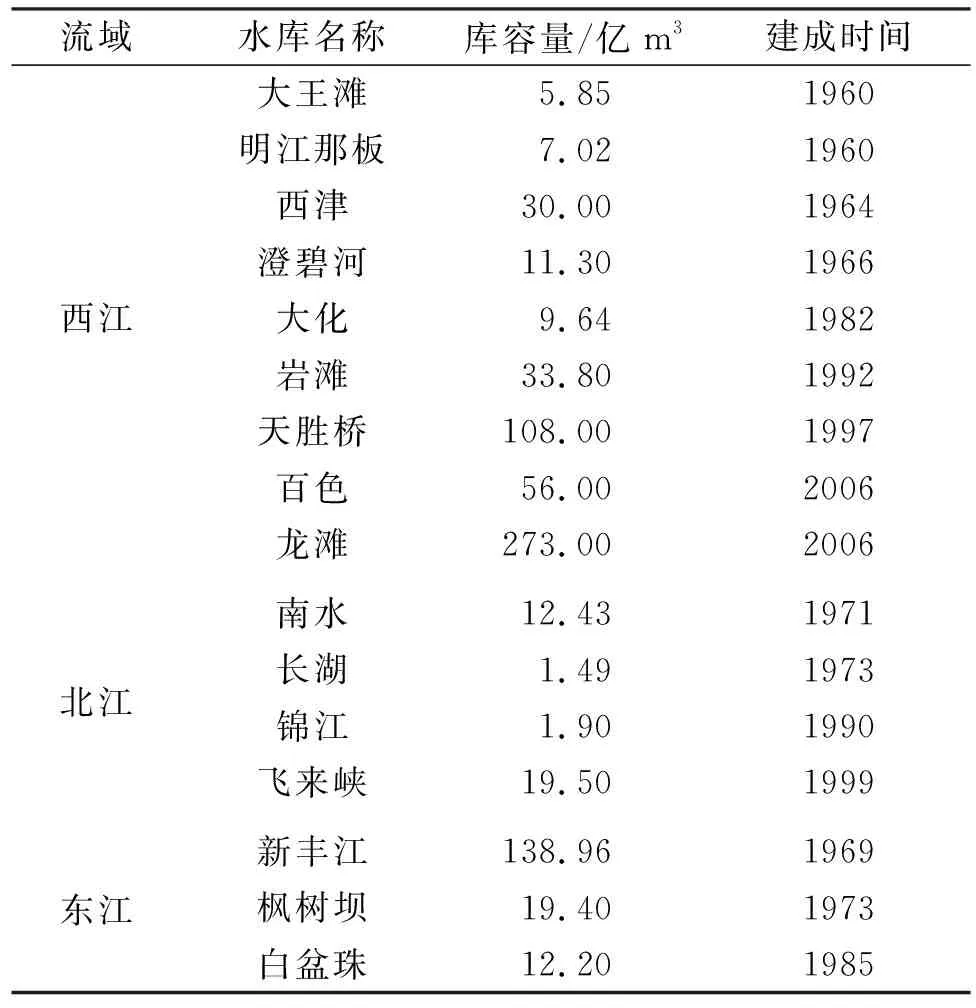
表4 珠江流域较大规模水库建设情况

图7 1960-2017年高要、石角、博罗分沙比

4 结 论

(1) 1960—2017年珠江流域主要水文站高要、石角、博罗站输沙率变差系数(Sv)值在0.5左右，总体数值较大，说明珠江流域输沙率年际变率较大，输沙率稳定性较差，而输沙率年际极值比显示北江与东江更易出现输沙率的极大值或极小值点，综合分析东江为三江中输沙率变异性最大的支流。

(2) M-K趋势分析、滑动平均法、累积距平法均显示1960—2017年珠江流域西江、东江输沙率下降明显，北江输沙率变化不大，高要站输沙率在2001年开始出现下降趋势，东江博罗站自1987年前后开始下降。

(3) 珠江流域西、北、东江输沙率年内分配极不均匀，输沙率的年内集中程度为西江高于北江高于东江，西江高要站年内输沙率主要集中在7月份，北江石角站输沙率集中期在5月、6月份交替出现，东江博罗站输沙率集中期在6月、7月份交替出现。

(4) 近几十年人类活动在珠江流域输沙率变化方面起着很大的作用，主要表现在流域大坝、水库的修建与由于政策与经济原因导致的水土流失的程度差异。