考虑后效性影响的梯级水库短期优化调度耦合模型研究

纪昌明，俞洪杰，阎晓冉，吴嘉杰，王丽萍

（华北电力大学 可再生能源学院，北京 102206）

1 研究背景

梯级水库短期优化调度［1-3］的主要任务是将长期经济运行分配给本短期运行周期的输入能在更短的时段内合理分配，以确定梯级水库短期最优运行方式。相比于中长期优化调度，短期优化调度的计算更加精确，对实际生产的指导意义更强［4］，因此它一直是研究的一大热点；但同时短期优化调度考虑的因素更为全面、复杂，尤其是水流滞时、尾水位变化后效性等因素的存在，也使它成为了研究的一大难点。

目前对梯级水库短期优化调度的研究多围绕“以电定水”或“以水定电”这两种运行模式单独展开，针对前者有梯级耗能最小模型、梯级蓄能最大模型等，后者有梯级发电量最大模型、梯级发电效益最大模型等［5］。Piekutowski等［6］针对澳大利亚的HEC水电系统建立了梯级耗能最小、梯级蓄能最大模型，通过模型求解有效减少了该梯级的发电耗能，使得其蓄能得到了明显的增加。纪昌明等［7］以梯级发电量最大为目标对雅砻江锦官电源组梯级进行了优化调度计算，大幅增加了该梯级的发电量；徐新黎等［8］在发电量的基础上考虑了分时电价的影响，建立了泸水河梯级发电效益最大模型，通过合理安排各电站在高峰期与低谷期的出力，实现了梯级发电效益的最大化。然而实际生产中调度情势多种多样，在一个梯级中可能出现两种运行模式并存的状况，此时该如何选取优化准则，构建相应的优化调度模型，目前尚未见到相关成果报道。

梯级水库上、下库之间存在一定的水力联系［9］，主要包括：（1）水量联系：上库出库流量在区间河道经过水流演进成为下库入库流量。（2）水头联系：下库会对上库尾水位产生顶托作用，影响上库的发电水头。目前的研究中，大部分都对上述两者进行了一定的简化处理，如：将上库出库流量直接作为下库入库流量，通过尾水位流量关系曲线计算上库尾水位，等等。上述简化处理忽略了水流滞时、尾水位变化后效性等因素的影响，使得模型计算结果与实际情况产生了偏差，降低了模型的计算精度。鉴于此，Ge等［10］通过建立水流传播时间与上库出库流量之间的非线性函数关系，实现了水流滞时的动态计算；纪昌明等［11］采用马斯京根法对上库出库流量进行了演进计算，较为精确地模拟了下库入库流量；徐鼎甲［12］通过研究水库下游非恒定流的变化规律，提出了一种高精度的尾水位计算经验方法。上述研究虽然对上下游水库间的水力联系进行了较为真实的模拟，但只是针对水量联系或水头联系两者之一，故其计算结果与实际仍存在一定的偏差。因此，同时考虑上下游水库间的水量、水头联系，准确模拟梯级水库的运行状况，对提高模型的计算精度有着重要意义。

短期优化调度多应用于生产实践，故除计算精度外，还对计算时间、效益等有着较高的要求。在求解水库优化调度模型的众多方法中，动态规划算法（Dynamic Programming，DP）以其全局收敛性、稳定性等优点而获得了广泛的应用，但是DP法存在维数灾［13］，并且无法处理后效性问题。纪昌明等［11］提出的MSDP法虽然能够解决后效性问题，但维数灾更为严重；梅亚东［14］提出的多维动态规划近似算法虽然计算量小，但在计算过程中采取了近似处理，故得到的解并非真正的全局最优解；另外，遗传算法［15］、粒子群算法［16］等现代智能算法虽然可以在较短时间内完成计算，但容易陷入局部最优，并且计算结果不够稳定。直到目前为止仍没有较为成熟的方法可以完全满足生产实践的要求，因此研发能够在较短时间内精确计算全局最优解的模型求解方法，是目前迫切需要解决的问题。

针对梯级水库短期优化调度在模型构建及求解等方面存在的不足，本文结合潘口、小漩梯级水电站耦合“以电定水”与“以水定电”两种运行模式的生产实际，运用BP神经网络研究上下游水库多时段之间的水量、水头联系，建立了考虑后效性影响的梯级水库短期优化调度耦合模型，并提出了伴随POA算法（Accompanied Progressive Optimality Algorithm，APOA）对其进行求解，以期为梯级水库短期优化调度生产实践提供有效的指导。

2 耦合模型

2.1 目标函数 梯级水库短期优化调度的目的就是通过合理配置各库的水能资源，提高梯级水电站的发电效益。而发电效益又可分为调度期内发电效益与未来发电效益两部分，其中前者可通过调度期内梯级发电量来表征（本文不考虑电价因素），后者可通过调度期末梯级蓄能来表征。从长远的角度来看，追求梯级发电效益最大即追求调度期内梯级发电量与调度期末梯级蓄能之和最大。在“以电定水”模式下，梯级总出力过程一定，即调度期内梯级发电量一定，上述目标可简化为追求调度期末梯级蓄能最大；在“以水定电”模式下，梯级各电站调度期末水位一定，即调度期末梯级蓄能一定，上述目标可简化为追求调度期内梯级发电量最大。而在实际生产中，由于所属调度部门等差异，同一梯级中各电站的运行模式可能不同，下面以潘口、小漩梯级为例对耦合运行模式下梯级水电站的目标函数进行介绍。

潘口、小漩梯级水电站是汉江水电开发有限责任公司（下称公司）下属的两个电站，其中潘口是湖北省重要的调峰电站，其电力调度归湖北省电力中调（下称电调），日常运行按电调指令进行，是典型的“以电定水”模式；下游的小漩是潘口的反调节电站，由公司自主优化调度，是典型的“以水定电”模式。虽然该梯级中两个电站的调度主体不同，但它们均由公司统一管理，故两者的决策主体是一致的，公司希望通过两库联合优化调度，提高梯级整体的发电效益。理论上来说，潘口按照电调指令发电，在厂内经济运行方式确定的情况下，并没有优化的空间。但长期生产实践发现，小漩回水对潘口尾水位具有一定的顶托作用：小漩维持高水位运行对自身发电有利，但这会使得潘口尾水位雍高，降低潘口机组的发电水头，进而影响其发电效率；相反，小漩降低运行水位虽然能够提升潘口的发电效率，但牺牲了自身的发电量。梯级间的水头联系使得两库联合优化调度成为可能，也为两种运行模式的耦合提供了契机，通过合理控制小漩运行水位，可以实现梯级发电效益的最大化。

在上述“以电定水”与“以水定电”模式耦合背景下，调度期内潘口发电量一定、调度期末小漩蓄能一定，此时追求梯级发电效益最大可简化为追求“调度期末潘口蓄能与调度期内小漩发电量之和”最大。因此本文从梯级总能量的角度出发，结合蓄能最大与发电量最大准则，构建潘口、小漩梯级水库短期优化调度耦合模型，目标函数如式（1）所示。需要说明的是，在调度期初潘口蓄能一定的情况下，调度期末潘口蓄能与调度期内潘口蓄能增量是一一对应的，鉴于蓄能增量的计算相对比较简单，故式（1）中以调度期内潘口蓄能增量来间接表征调度期末潘口蓄能；另外，当潘口入库流量较小且发电任务较大时，其动用库蓄水量发电，蓄能呈减小趋势，可能出现目标函数为负值的现象。

式中：Ec为耦合运行模式下梯级水电站的发电效益；T为计算时段数；Qi，t为水库i在t时段的入库流量，潘口对应i=1，小漩对应i=2；qi，t为水电站i在t时段的发电流量，本文不考虑弃水，发电流量即出库流量；λi为水电站i的能效系数；Ni，t为水电站i在t时段的出力；Δt为计算时段长。

2.2 约束条件 既然耦合模型是针对两种运行模式并存状况提出的，那么其约束条件中必然含有两者特有的约束条件：潘口在“以电定水”模式下，需要满足出力指令约束，即电站各时段出力均等于电调指令，具体见式（2）；小漩在“以水定电”模式下，需要满足调度期末水位约束，即需要确定其在调度期末的库水位，具体见式（3）。

式中：Hi，t为水电站i在t时段的发电水头；N′t为潘口在t时段的规定出力；Zi，t为水库i在t时刻的水位；DZi，t为水电站i在t时段的尾水位；Zend为小漩在调度期末的控制水位。

其余约束为两电站共有的约束，包括水位、出力、流量上下限约束以及水量平衡约束，具体见式（4）—式（7）。需要说明的是，电调下达的指令中潘口规定出力位于出力上下限之间，故式（2）与式（5）不存在矛盾。

3 上下游水库水力联系研究

3.1 考虑水流滞时及区间入流的下库入库流量计算 梯级水库中下库入库流量由上库出库流量与区间入流共同组成。上库出库流量流达下库存在水流滞时，主要包括：（1）水流从上库到达下库需要一定的传播时间；（2）由于上库出库水流为非恒定流，其在传播过程中，既要位移，又要坦化。图1为某场发电过程中潘口的出库以及小漩的入库流量过程，由图1可得，相比于潘口出库流量，小漩入库流量的起涨、回落时间均有一定的滞后，并且后者的曲线较前者更加平缓。在考虑水流滞时的情况下，潘口出库流量何时流达、以什么样的流量过程流达小漩水库是一个复杂的水力学问题。

潘口、小漩坝址仅相距10.4 km，区间集水面积很小且无支流汇入，实际生产中往往忽略区间入流。但通过长期监测数据发现，小漩入库流量的平均值略大于潘口出库流量（两者差值约为5 m3/s），故为了提高模型计算精度，本文考虑区间入流的存在。潘口、小漩区间入流主要由区间流域产汇流形成，很大程度上取决于该流域的降雨量。在考虑区间入流后，小漩入库流量的计算变得更加复杂，既包括水流在河道中的演进过程，又涉及从降雨到产汇流等一系列的水文循环过程。目前对于这些自然过程的物理机制尚未完全了解，精确模拟这些过程存在一定难度，故本文利用BP神经网络［17］从大量数据中寻找小漩入库流量与潘口出库流量、区间流域降雨量之间关系，并对其进行精确计算。

图1 潘口出库、小漩入库流量对比

图2 小漩入库流量计算结果

BP神经网络是一种按误差逆向传播算法训练的多层前馈网络，从结构上讲，其一般分为一个输入层、一个输出层与若干隐含层。在小漩入库流量计算中，输出层为本时段小漩入库流量Q2，t；根据实际调度经验，将本时段以及前4个时段的潘口出库流量q1，t—q1，t-4、区间流域降雨量Pt—Pt-4作为初选输入层数据，采用相关系数法对其进行筛选，计算结果如表1所示。由表1可得，随着时间的提前，潘口出库流量与小漩入库流量的相关系数逐渐减小，q1，t、q1，t-1、q1，t-2与Q2，t的相关系数相差不大，但q1，t-3、q1，t-4与Q2，t的相关系数较前三者明显减小，这说明潘口出库流量到达小漩的时间在0～2个时段之间。根据上述结果，从潘口出库流量中选取q1，t、q1，t-1、q1，t-2作为输入层数据。与潘口出库流量相比，区间流域降雨量与Q2，t的相关系数明显偏小，并且其值随时间变化不大。考虑到区间入流客观存在但仅占小漩入库流量的很小一部分，从区间流域降雨量中选取与Q2，t相关系数最大的Pt-1作为输入层数据；隐含层是整个神经网络的计算核心，1989年，Robert证明了3层网络（一个输入层、一个输出层与一个隐含层）可模拟任意复杂的非线性问题，故此处设置一个隐含层，隐含层节点数按照下式［18］确定：

式中：h为隐含层节点数；u为输入层节点数；v为输出层节点数；a为0～10之间的调节系数，通过试算，本文中a=4时神经网络的训练效果最好。

表1 潘口出库流量、区间流域降雨量与小漩入库流量的相关系数

在确定神经网络结构之后，输入2012—2016年的历史数据对神经网络进行训练，神经元传递函数取双曲正切函数，训练次数取10 000次，训练完成后保存网络，后期即可利用该网络对小漩入库流量进行计算。图2显示了前述发电过程中BP神经网络计算所得的小漩入库流量过程，与实际相比，其相对误差为1.11%。而采用动态滞时法［10］（仅考虑水流传播时间，不考虑水流坦化，具体传播时间见表2）进行计算时，相对误差为3.88%。两者相比，BP神经网络的计算结果更加精确。

表2 水流传播时间

3.2 考虑双重后效性因素影响的上库尾水位计算 梯级水库中上库尾水位与下库库水位有着密切的联系。与天然情况相比，小漩坝前回水会抬高区间河道的水位，导致潘口尾水位雍高。小漩库水位不同，其对潘口尾水位的顶托程度也不同，图3展示了小漩在不同库水位状态下对应的潘口尾水位流量关系曲线。然而通过长期生产实践发现，采用水位流量关系法计算得到的潘口尾水位与实际存在较大偏差，究其原因可知：尾水位流量关系曲线是在假设出库水流为恒定流的基础上得到的，而实际上出库水流属于非恒定流，非恒定流的特性导致尾水位变化具有一定的后效性，即本时段的尾水位与其前一时段的尾水位有关［12］；另外，小漩回水到达潘口坝下需要一定的时间，因此影响本时段潘口尾水位的并不一定是本时段的、还可能是前若干时段的小漩库水位，这也导致了潘口尾水位变化具有一定的后效性。在双重后效性因素的作用下，本时段潘口尾水位受本时段潘口出库流量、前一时段潘口尾水位以及前若干时段小漩库水位的三重影响，物理机制十分复杂，故本文仍采用BP神经网络进行计算。

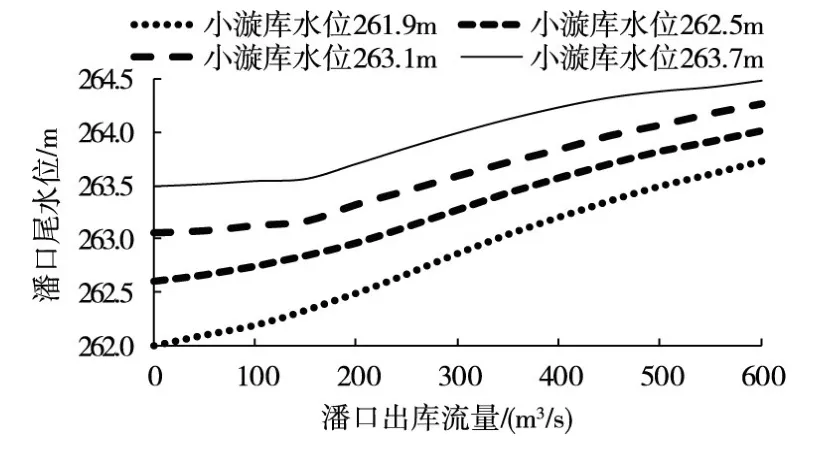
图3 潘口尾水位流量关系曲线

图4 潘口尾水位计算结果

在潘口尾水位计算中，输出层为本时段潘口尾水位DZ1，t；输入层数据中，除了本时段潘口出库流量q1，t、前一时段潘口尾水位DZ1，t-1以外，还需确定是哪些时段的小漩库水位。同样的，将本时段以及前4个时段的小漩库水位Z2，t—Z2，t-4作为初选输入层数据，采用相关系数法对其进行筛选，计算结果如表3 所示。由表3 可得，Z2，t、Z2，t-1、Z2，t-2与 DZ1，t的相关系数相差不大，但 Z2，t-3、Z2，t-4与DZ1，t的相关系数较前三者明显减小，因此从小漩库水位中选取Z2，t、Z2，t-1、Z2，t-2作为输入层数据。隐含层以及训练参数的设置与3.1节类似，训练完成后保存网络，后期即可利用该网络对潘口尾水位进行计算。图4显示了前述发电过程中BP神经网络计算所得的潘口尾水位过程，与实际相比，其计算误差为0.001 m，明显小于水位流量关系法的计算误差（0.027 m），这也说明了BP神经网络的优越性。

表3 小漩库水位与潘口尾水位的相关系数

4 模型求解

在考虑了水流滞时、尾水位变化后效性等影响因素后，梯级水库本时段的决策（发电流量）不仅与本时段的状态（库水位）有关，还与之前若干时段的状态有关，其短期优化调度模型已不满足“无后效性”条件，无法采用DP法求解。文献［11］中提出的MSDP法虽然能够处理后效性问题，但仍然不能避免维数灾。以本文的研究对象为例对维数灾进行说明，虽然潘口、小漩梯级水库短期优化调度是一个两库联调问题，但由于潘口为“以电定水”模式，一旦小漩的运行状态确定（即小漩对潘口尾水位的顶托程度确定），潘口只需通过厂内经济运行计算，运行状态也随之确定，因此其实质上是一个一维问题。在一维情景下，假设库水位离散点数为D，相关联的时段数为R，即前R-1个时段的状态对本时段的决策有影响，则MSDP法每次多阶段计算时小漩有DR+1种水位组合，考虑T个多阶段后总计算量为T·DR+1。T·DR+1的值随着R的增大呈指数形式增长，故即使在一维情景下，由于考虑了R个时段的关联，MSDP法也出现了维数灾。当问题的维数增加到L（L＞1）维时，每次多阶段计算时水位组合有（DR+1）L种，总计算量为T·（DR+1）L，维数灾更加突出。鉴于此，本文提出一种改进的POA算法即APOA法对有后效性的梯级水库短期优化调度模型进行求解。

4.1 APOA法求解思路 POA法［19］是动态规划法的一种改进算法，它把复杂的多阶段决策问题简化为一系列的二阶段决策问题，大幅降低了问题的复杂程度，有效缓解了维数灾问题。与POA法相比，APOA法的改进体现在以下两个方面：

（1）对小漩进行寻优计算的同时，将潘口库水位作为小漩库水位的空间伴随变量进行计算。每次离散计算时，本时段以及之前时段小漩的库水位已确定，故小漩对潘口尾水位的顶托程度也已确定，又由于潘口上一时段的尾水位已知，故本时段潘口尾水位只与本时段潘口出库流量有关，在潘口出力一定的情况下，通过试算即可求得其出库流量，再根据潘口的出、入库流量计算得到潘口库水位。因此，对于小漩的每一个离散水位，潘口都有唯一一个库水位与之对应，进而对于调度期内小漩的每一条水位过程线，潘口都有唯一一条水位过程线与之对应。

（2）每次两阶段计算时，将前R-1个关联时段的变量作为本时段的时间伴随变量参与计算。由于考虑了R个时段之间的关联，当前两阶段的决策与前R-1个时段有关。如图5所示，APOA法将T时段的问题划分T-1个子问题，每个子问题包含两个主要计算时段以及伴随的R-1个关联时段。当计算至由t时段、t+1时段组成的两阶段时，其他时段（包括伴随的R-1个关联时段）的状态与决策均已知，因此其能够有效处理后效性问题。APOA法每次两阶段计算时，小漩有D种水位组合，一次迭代需要进行T-1次两阶段计算，故计算量为（T-1）·D，假设K次迭代后满足精度要求，则总计算量为K·（T-1）·D，明显小于MSDP法的T·DR+1，因此APOA法能有效缓解维数灾问题。

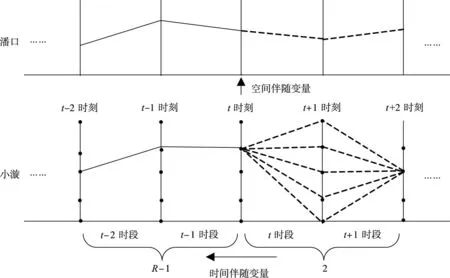
图5 APOA法示意图

4.2 APOA法求解步骤 APOA法的求解步骤表示如下，其计算流程图见图6。

（1）确定关联时段数。通过相关系数法确定与本时段有水量、水头联系的时段数，若前r1个时段与本时段小漩入库流量相关，前r2个时段与本时段潘口尾水位相关，则可通过式（9）计算关联时段数，本文中r1=2，r2=2，则R=3。

（2）训练BP神经网络。输入训练数据对BP神经网络进行训练，训练数据的类型、起止时间以及神经网络的结构、参数设置详见3.1及3.2节，训练完成后得到计算小漩入库流量的神经网络net1以及计算潘口尾水位的神经网络net2。

（3）确定初始解。初始解的选取对APOA法的计算时间有着重要影响［20］。水电站的调度规则凝聚着调度人员长期以来的调度经验，根据调度规则计算得到的解往往是较优解，故本文将该解作为初始解。需要说明的是，小漩初始水位过程线才是初始解中最为关键的变量，潘口初始水位过程线只是前者的伴随变量而已。

图6 APOA法计算流程图

（4）逐步优化计算。从1时段开始到T时段进行逐步优化计算，当计算至由t时段、t+1时段组成的两阶段时（伴随t-2时段、t-1时段这两个关联时段），固定除t+1时刻以外所有时刻的小漩库水位，对t+1时刻的小漩库水位离散点进行遍历计算。其中小漩入库流量、潘口尾水位采用BP神经网络算得，计算公式见式（10），潘口库水位作为小漩库水位的伴随变量进行计算。遍历完所有离散点后，筛选出t+1时刻小漩的最优水位以及与之对应的潘口最优水位令

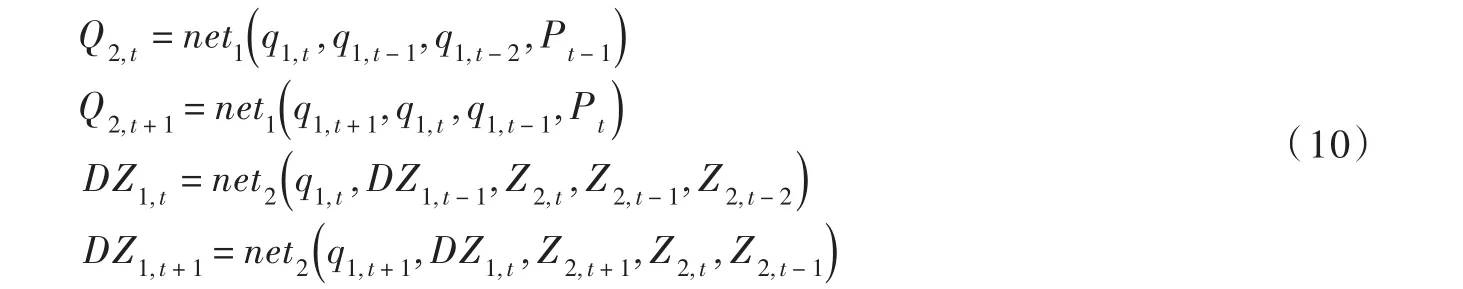
（5）迭代计算。执行完步骤4，APOA法的第一次迭代计算完成，得到新的解伴随比较与对应的目标函数，若两者之差小于计算精度ε，满足收敛条件，则将（伴随）作为最终解输出，停止计算；否则将作为新的初始解，重复步骤4，直至满足收敛条件为止。

5 实例计算

堵河流经陕西省、湖北省，是汉江南岸的一级支流，潘口、小漩梯级水电站位于堵河上游湖北省境内，其基本参数见表4。在“以电定水”模式下，潘口水电站每日按照电调下达的96点负荷曲线指令进行发电，故本文取调度期为1日，计算时段数为96，相应的每个计算时段长15 min。

以2016年12月10日为例，建立潘口、小漩梯级水库短期优化调度耦合模型，分别采用DP法、POA法、MSDP法以及APOA法对模型进行求解，其中MSDP法与APOA法考虑了后效性因素，采用BP神经网络计算小漩入库流量以及潘口尾水位，而DP法与POA法未考虑，将潘口出库流量直接作为小漩入库流量，并且采用水位流量关系法计算潘口尾水位。在求得4种方法对应的优化调度方案后，将4个调度方案执行，即通过“潘口按出力控制、小漩按水位控制”的方式进行仿真计算，得到结果如表5所示。

表4 梯级水电站基本参数

表5 各方法计算结果

5.1 发电效益分析 以目标函数的大小来表征各方法对应的发电效益，目标函数越大，发电效益越高，相应的方法也就越优。MSDP法已被理论证明具有全局收敛性，由表5可得，上述实例中，在计算条件相同（均考虑了后效性因素并且离散点数相同）的前提下，APOA法与MSDP法的目标函数完全一致，这初步证明了APOA法的优越性。为了增加该结论的代表性，本文又选取了30个代表日进行计算，结果显示，30个代表日中有22 d两者的计算结果完全一致，其余8 d两者的计算结果也非常接近，这再一次验证了APOA法的优越性。

接下来对APOA法的发电效益进行具体分析。2016年12月10日APOA法的计算结果中，潘口的蓄能增量为-13.74万kW·h，比实际少0.10万kW·h，小漩的发电量为29.87万kW·h，比实际多3.10万kW·h，故从梯级角度来看，APOA法对应的目标函数比实际大3.00万kW·h，占该日梯级总发电量的1.67%。上述结果表明，相比于目前实际采用的调度方式，使用本文提出的耦合模型进行优化调度能够明显提升梯级水电站的发电效益。

同样的，POA法与DP法的对比结果也证明了POA法的优越性。但由表5可得，DP法、POA法的计算结果与MSDP法、APOA法存在差异，这是由于它们的计算条件不同所造成的。DP法、POA法未考虑后效性因素，计算精度不高，因此其对应的优化调度方案在执行后，梯级水库的运行过程与优化调度方案有所差异，发电效益较预期也有一定程度的减小，这就使得它们两者的目标函数小于MSDP法、APOA法。

5.2 计算时间分析 本实例中DP法的计算量为T·D2，当增加考虑后效性因素后，MSDP法的计算量为T·DR+1，本次计算取离散点数D=200，关联时段数R=3，故理论上MSDP法的计算量为DP法的40 000倍。但由表5可得，MSDP法的实际计算时间约为DP法的1050倍，远小于40 000，这是因为本文在MSDP法计算时对可行域进行了约束，对不满足约束的离散点并不进行遍历计算，因此节省了大量计算时间。尽管如此，其计算时间仍长达2.13×105s（约2.5 d），不满足生产实践对时效性的要求。

POA法是为了缓解DP法维数灾而提出的一种改进算法，其计算量明显小于DP法，这从表5显示的计算结果中就能得到很好的证明。由POA法变化至APOA法时，虽然增加考虑了后效性因素，但计算量依旧保持为K·（T-1）·D的形式。两种方法在迭代次数K上可能存在差异，但由该差异引起的计算量变化呈线型，并非指数型，故并不明显。由表5可得，本实例中APOA法的计算时间为18.77s，与POA法基本相同，但仅为MSDP法的1/11348，这说明在得到相同计算结果的情况下，APOA法相比于MSDP法极大地缩短了计算时间，因此其能够满足生产实践对时效性的要求。

5.3 计算精度分析 从优化调度方案（未执行的）与实际过程接近程度的角度对各方法的计算精度进行分析。由图7（a）可得，APOA法对应的潘口出库流量过程线与POA法基本重合，两者仅存在细微差别，究其原因可知：潘口是一个高水头电站，影响其发电效率的主要因素是流量而并非水头，因此在不同的顶托程度下，潘口完成相同的发电任务，发电流量相差很小。在潘口出库流量相差不大的情况下，APOA法与POA法对应的潘口尾水位却存在明显差异，图7（b）中POA法对应的潘口尾水位过程线与潘口出库流量过程线形状高度相似，呈现陡涨陡落的现象，而在实际生产中，潘口尾水位的变化是一个连续的、相对缓慢的过程。POA法计算时采用的水位流量关系法仅考虑了本时段潘口出库流量、小漩库水位对潘口尾水位的影响，忽略了尾水位变化的后效性，故计算结果与实际不符。而APOA计算时采用的BP神经网络则综合考虑了影响潘口尾水位的各个因素，其得到的尾水位过程线形状相对平缓，与实际情况更为接近。因此从潘口尾水位的角度来看，APOA法比POA法计算精度更高。

图7 潘口计算结果对比

图8 小漩计算结果对比

接下来从小漩入库流量计算精度的角度进行分析。由图8（a）可得，由于计算过程中考虑了水流滞时，APOA法对应的小漩入库流量过程线较POA法略靠后，并且曲线更加平滑。小漩入库流量过程的不同，导致了两种方法最终得到的小漩库水位过程（图8（b））、小漩出力过程（图8（c））也有所不同，特别是在潘口开、停机的邻近时段，两者的差异较为明显。以潘口开机的邻近时段为例进行分析，该日潘口水电站在6∶30之前一直处于停机状态，出库流量为0，自6∶30接到电调指令后开始发电，6∶30—6∶45时段出库流量为125 m3/s，POA法将潘口出库流量直接作为小漩入库流量，认为该时段小漩入库流量为125 m3/s，因此小漩水电站该时段以16.7 MW的出力运行，发电流量为140 m3/s，库水位略有下降。而由表2可得，125 m3/s对应的流量量级较小，需要两个时段才能到达小漩水库，故小漩在该时段只有少量区间流量入库，无法满足以16.7 MW的出力运行并且保持库水位略微下降的状态。由上述分析可得，由于小漩入库流量计算精度较低，POA法计算所得的调度方案违背了自然规律，在执行时梯级水库无法完全按照该方案运行。而APOA法的计算结果中，小漩库水位在7∶00之后才开始抬高，此时潘口在6∶30—6∶45时段的出库流量已基本到达小漩水库，因此小漩能够遵循水量平衡规律，既下泄流量进行发电、又不断抬高库水位。综上，由于BP神经网络在小漩入库流量计算中的优异表现，APOA法所得调度方案的精度比POA法更高。

6 结论

本文在总结了单一运行模式下各类优化调度模型的基础上，结合潘口、小漩梯级水电站的生产实际，提出了“以电定水”与“以水定电”耦合模型，该模型兼顾了潘口的发电效率与小漩的发电量，从梯级总能量的角度出发追求梯级整体发电效益最大化，能够很好地契合实际生产的需求；考虑了水流滞时以及尾水位变化后效性等影响因素，采用BP神经网络实现了小漩入库流量、潘口尾水位的精确计算，并提出了APOA法对有后效性的梯级水库短期优化调度耦合模型进行求解，显著提高了模型的计算精度。实例计算结果表明：本文所建模型科学合理，通过模型计算能够有效提高梯级水电站的发电效益；APOA法能够对所建模型进行高效求解，并且保证计算结果的优越性、精确性，满足生产实践的要求。