变化环境下时变标准化径流指数的构建与应用
李 敏,李建柱,冯 平,陈 亮
(天津大学 水利工程仿真与安全国家重点实验室,天津 300350)
1 研究背景
20世纪以来,干旱成为了亚洲地区影响力最广泛的自然灾害之一,超过6百万的人死于干旱,11亿人受到影响,并能够引起粮食危机、生态环境恶化等[1-3]。美国气象学会将干旱分为4种类型;气象干旱、水文干旱、农业干旱与社会经济干旱[4]。水文干旱是自然干旱中的一种重要类型,关系着水文循环和水量平衡,并且对人类用水有着直接的影响。为了分析水文干旱特征,国内外学者提出了多种干旱评估指数,如标准化径流指数SRI(standardized runoff index)、累计流量距平、地表供水指数SWSI(surface water supply index)、河川径流干旱指数SDI(Streamflow Drought Index)、标准化径流指数SSI(Standardized Streamflow Index)等[5-10]。通过计算干旱评估指数,可以客观地确定干旱历时、干旱烈度与干旱频率,进而准确地反映干旱的特征及变化规律。
Milly等[11]指出,在气候变化和人类活动的共同作用下,基于一致性假设的水文频率计算理论和方法将面临失真。因此,研究变化环境下的水文干旱演变规律,成为目前干旱领域研究的热点与难点。Russo等[12]提出了基于GAMLSS模型的非一致性干旱指数SnsPI(Stationary and non-stationary Standardized Precipitation Index),该指数考虑了变化环境下降水序列服从的Gamma分布的参数μ为时间的函数,并应用该指数分析了变化环境下欧洲极端干湿状况。应用结果也表明,SnsPI的计算原理更合理,能够较好地反映实际干湿状况。Li等[13]建立了以气候因子为协变量的非一致性模型,提出了非一致性标准化降水指数(NSPI),结果表明,NSPI指数比传统的指数SPI更好的反映出滦河流域的干旱特征。Wang等[14]假设滦河流域夏季降水序列服从参数μ随时间变化的Gamma分布,计算了基于GAMLSS模型的SPIt指数。结果表明以时间为协变量的指数SPIt对滦河流域的气象干旱评价效果优于传统的SPI指数。
目前针对水资源、洪水频率进行非一致性的研究较多[15-18],而对变化环境条件下形成的非一致性干旱特征分析的研究较少。Shukla等[5]类比SPI指数[19]的理论建立了标准化径流指数SRI来评价干旱。
SRI在实际应用中具有和SPI相同的优势,该指数计算简单,所需输入数据单一且容易获得,适用于多时间尺度计算,可以满足不同地区、不同应用的需求,能够为不同时间尺度的干旱监测服务。本文以SRI指数为基础,提出了变化环境下时变标准化径流指数SRIt,即假设径流序列为二阶非平稳序列,序列服从Gamma分布的两参数μ、σ均随时间变化,充分考虑了径流序列分布参数随时间变化的可能性,以研究区域历史干旱事件为研究对象,对比分析传统SRI和SRIt的评价结果,以验证该指数的合理性。
2 研究区域概况
潘家口水库流域位于河北省唐山市与承德地区交界处,面积约为3.37万km2,占滦河流域总面积的75%。流域属副热带季风区,春季少雨,夏季多雨,冬季雨雪稀少,易旱灾。流域多年均气温为5~12℃,多年平均降水量在400~700 mm之间,年内分配不均,主要集中在夏季,夏季降水量在200~560 mm之间。年水面蒸发量在950~1150 mm之间。流域径流年际丰枯变化比较悬殊,常出现连续丰水年和枯水年,多年平均径流量为24.5亿m3。根据历史资料记载[20],在 1949—2010年期间,滦河流域的主要干旱灾害发生于1961、1963、1968、1972、1980—1984、2000、2007及2009年。近年来,由于全球气候变化和流域人类活动的影响日益加剧,滦河流域降水量和径流量均明显趋于减少,干旱现象频发,特别是2000年以后,流域极端干旱和连年干旱频繁出现。干旱事件的频发造成流域大面积受灾,损失严重,制约了流域经济和社会的发展。研究区域位置及区域内各水文站点分布如图1。
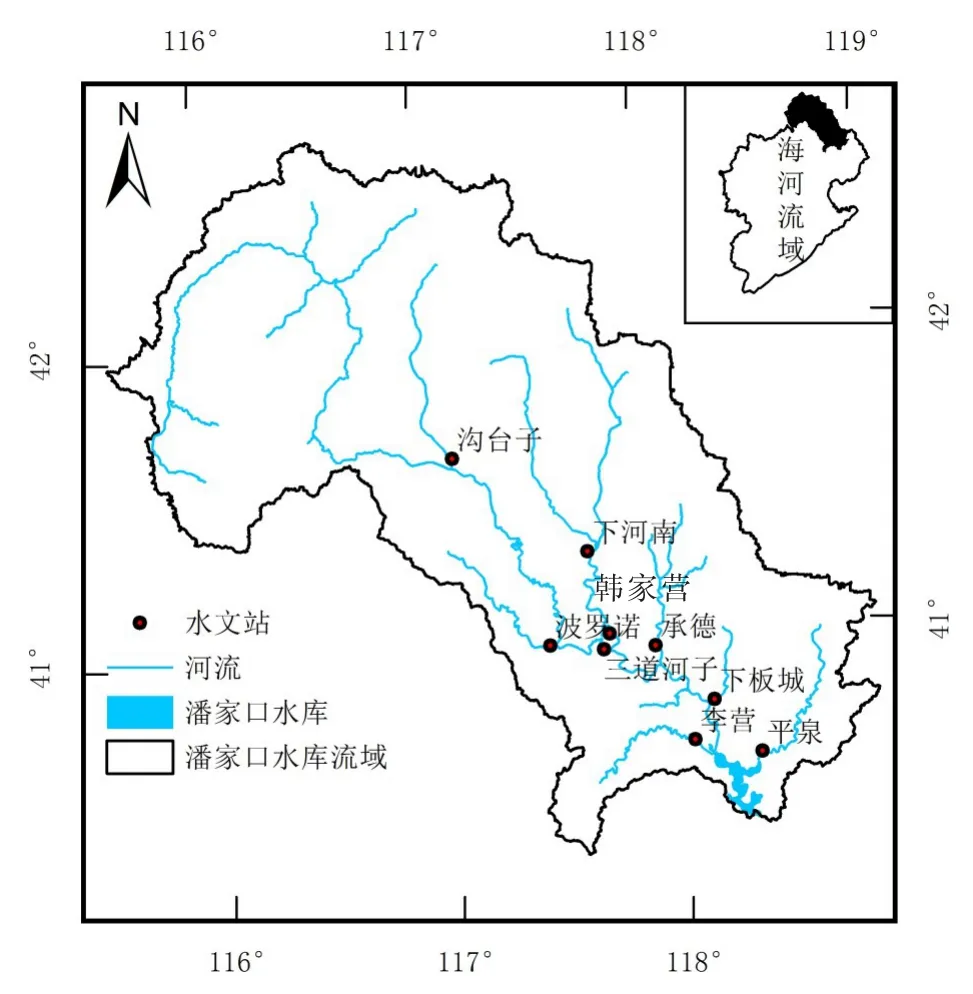
图1 潘家口水库流域地理位置及9个水文站分布
3 研究方法
3.1 标准化径流指数SRI 标准化径流指数SRI是由Shukla和Wood[5]于2008年首次提出的水文干旱指数,SRI的计算就是将给定时间尺度的累积径流量的分布通过等概率变换转化为标准正态分布。一定时间尺度的累计径流量的计算公式如下:

式中:v表示年份;τ表示月份;k为给定的时间尺度;为给定时间尺度k下的累积径流量,m3;x为τ-i月的月径流量,m3。本文选用两参数的Gamma分布作为一定时间尺度的累积径流量的分布线型。两参数Gamma分布概率密度函数的表达式为:
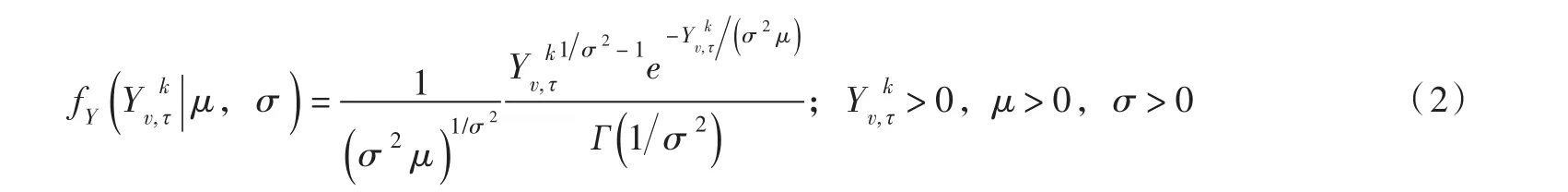
时变标准化径流指数SRIt本文基于GAMLSS模型构建以时间为协变量的非一致性模型。在假设水文序列所服从的分布线型不变时,该模型能够灵活地模拟概率分布的参数随协变量的变化[21]。模型的参数估计方法采用极大似然法,模型的评价准则采用全局拟合偏差GD(Global Deviance,GD)、AIC(Akaike Information Criterion)准则[22]和 SBC(Schwarz Bayesian Criterion)[23]准则,判断准则指数越小,模型模拟效果越好。为了避免回归方程太过复杂,本文将多项式次数的上限设定为二次,即n范围为0~2。
在时变矩模型中,假设实测径流序列的分布参数是时间t的函数,即:

本文采用n次多项式来描述分布参数μ、σ与时间t之间的关系,表示为:

式中,a0、b0为常数项,ai、bi为多项式系数,i=0,1,2,…,n。
为了比较两参数随时间的变化,本文分别建立两参数μ、σ均为常数,即均不随时间变化、单个参数μ随时间变化、两参数μ、σ均随时间变化的三种模型(i=0,1,2),并且基于三种模型采用全局拟合偏差GD、AIC准则和SBC准则分别选出拟合效果最好的最优模型,分别记为模型1、模型2与模型3。
本文通过计算模型残差的均值、方差、偏态系数、峰态系数和Filliben系数以及Worm图来评价最优模型的构建是否合理。若最优模型残差序列的均值接近于0,方差接近于1,偏态系数接近于0,峰态系数接近于3,Filliben系数大于等于标准值,则认为残差序列近似服从标准正态分布,最优模型构建合理。

表1 SRI与SRIt分级标准及相应阈值
由于标准化径流指数SRI的计算类似于SPI指数,因此,选用与SPI相同的干旱等级划分标准[13]。指数的正值表示湿润状况,负值表示干旱状况。
4 结果与分析
4.1 径流序列非一致性识别 本文采用Mann-Kendall[24]检验法,对研究区域9个水文站1960—2011年的12个月时间尺度的累计径流量序列进行趋势分析,分析结果如表2。从表2得出,研究区域9个水文站的径流序列均呈现下降趋势,且除沟台子站与韩家营站以外,其余站点的的径流序列呈显著下降趋势。

表2 潘家口水库流域9个水文站径流序列趋势检验结果
4.2 模型评价 以潘家口水库流域波罗诺站为代表,以逐月实测径流数据为基础分别建立一致性模型1、以单参数μ随时间变化的非一致性模型2、以两参数μ、σ均随时间变化的非一致性模型3,并分别通过GD、AIC和SBC准则确定各自的最优模型,由于径流序列一般具有年尺度的周期性,具有代表和实践意义,因此,本文以12个月时间尺度展开分析。波罗诺站12个月时间尺度的逐月径流系列的3种模型的GD、AIC、SBC见表3。由表3可知,对于波罗诺站12个月尺度的逐月累计径流分析序列,模型3的3个指数整体上最小,拟合效果最优,其次为模型2。
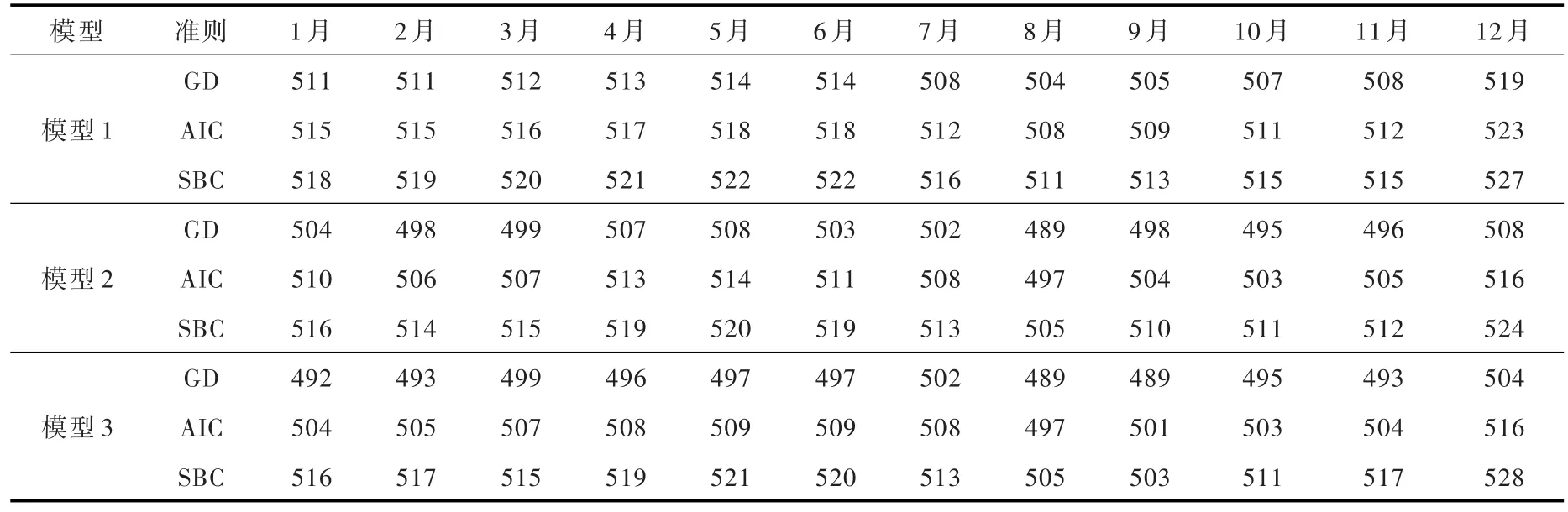
表3 波罗诺站12个月时间尺度的逐月径流系列模型的GD、AIC、SBC
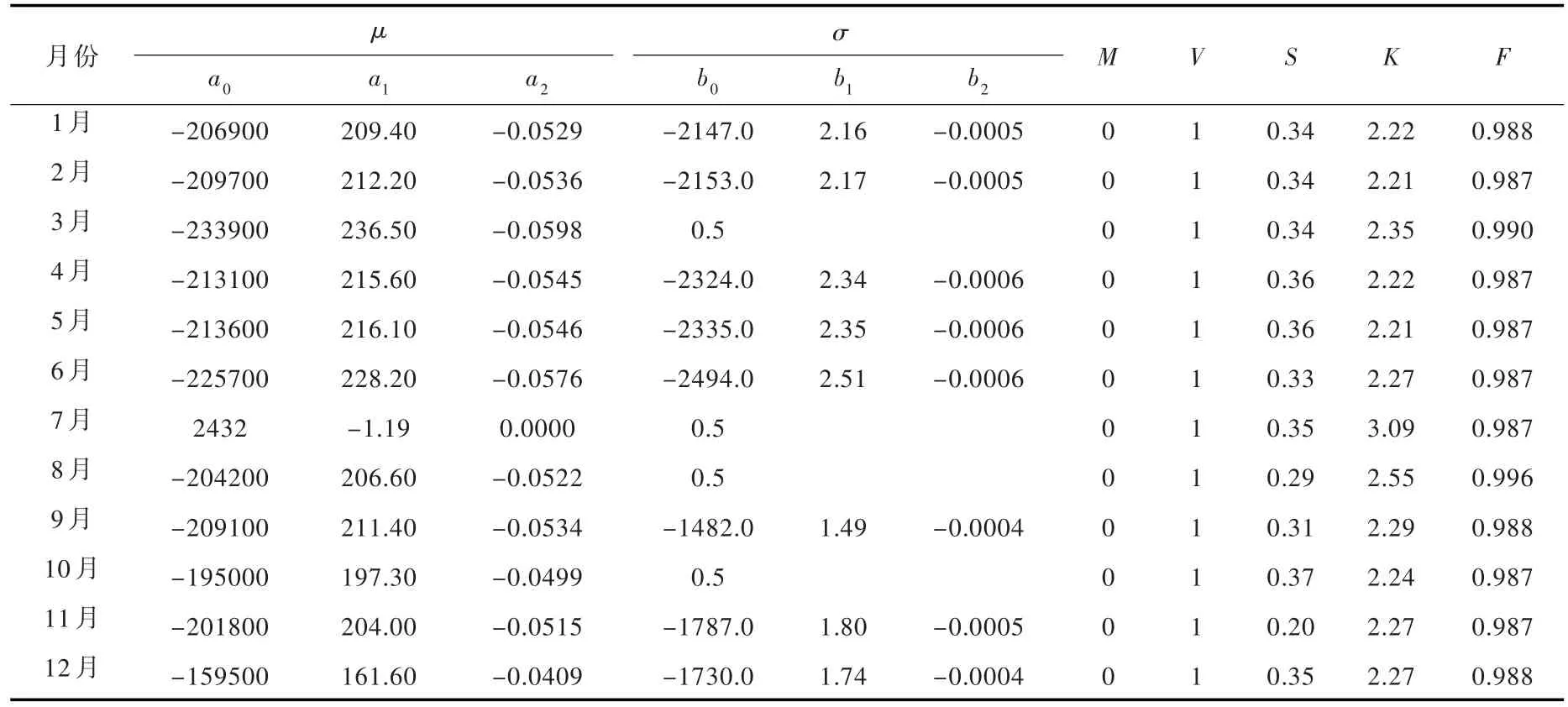
表4 波罗诺站逐月的12个月时间尺度最优模型参数
表4列出了波罗诺站逐月的12个月时间尺度最优模型参数,从表4中看出,每个月的参数均与时间t有关。对于所采用的径流样本序列长度为52,当Filliben系数≥0.978时才通过显著性水平为95%的检验[25]。波罗诺站逐月的的12个月时间尺度的最优模型残差的均值、方差、偏态系数、峰态系数和Filliben系数均符合标准,认为各站的最优模型构建合理。
图2展示了波罗诺站1960—2011年累计径流序列的残差worm图及分位数灰度图,由于篇幅的限制,以12月份的12个月时间尺度为例说明。图2(a)为累计径流序列的最优模型(模型3)下的残差worm图,所有残差点均处在两条椭圆曲线包围的“可接受”区内,表明Gamma分布对径流序列的拟合效果较好。由图2(b)—(d)中的分位数灰度图可以看出,实测点据在最优时变矩模型(模型3)中的分位数灰度图中的分布状况明显更合理。模型1在0~50%分位数区间覆盖了53%的实测点,25%~75%分位数灰度区间覆盖了73%的实测点据;模型2在0~50%分位数区间覆盖了54%的实测点,25%~75%分位数灰度区间覆盖了76%的实测点据;而模型3在0~50%分位数区间覆盖了58%的实测点,25%~75%分位数灰度区间覆盖了77%的实测点据。因此,模型3对径流实测点据的拟合效果更好,较好地描述了径流数据的非线性随机变化。此外,从模型3可以看出,波罗诺站径流量序列整体上呈下降趋势,与Mann-Kendall趋势分析结果一致,且约在1960—1980年为增加趋势,在1981—2011年为下降趋势,1980年左右为径流量序列的可能变异点,尤其是上浅灰色的变化趋势尤为明显,这与Li[26],Wang[27]分析的结果一致,也证明了模型3具有较好的拟合效果。
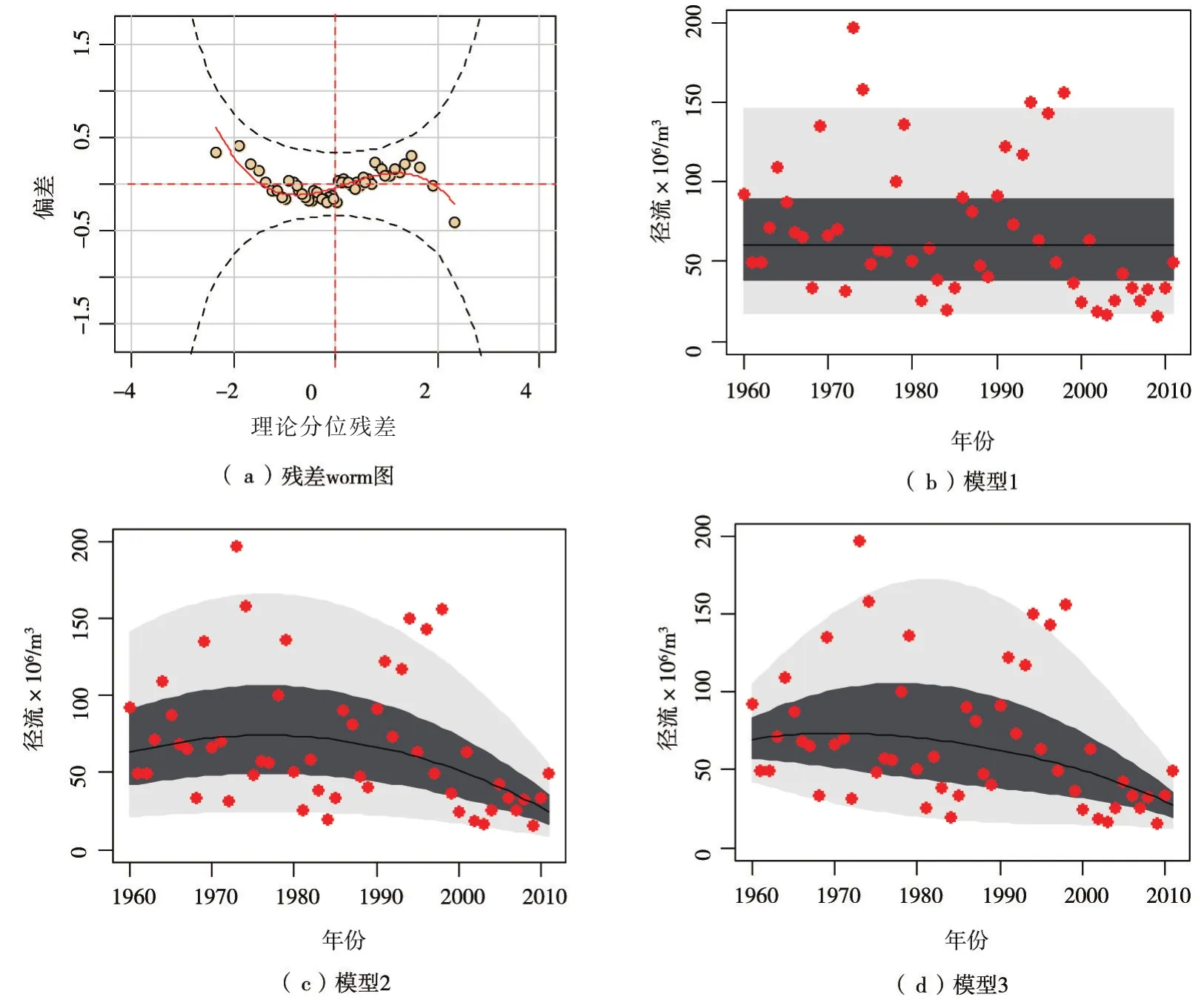
图2 波罗诺水文站1960—2011年12月份12个时间尺度的累计径流序列模型3的Worm
通过比较模型1、模型2、模型3的GD、AIC、BIC值,选出3种模型中GD、AIC、BIC值最小的模型作为研究区域各水文站的最优模型。表5展示了潘家口水库流域各水文站12个月时间尺度的累计径流量的最优模型参数,考虑到篇幅的限制,只列出12月份最优模型参数。可以看出,沟台子站与韩家营站径流量序列的Gamma分布的参数μ、σ均为常数,即最优模型为模型1,该结果与Mann-Kendall趋势检验的结果一致,认为两个站的径流序列非一致性特征不明显;三道河子站与波罗诺站的参数μ、σ均表现出与时间t的相依关系,即最优模型均为模型3;其余站点的参数μ与时间t存在相依关系,σ为常数。此外,表5中各水文站的最优模型残差的均值、方差、偏态系数、峰态系数和Filliben系数均符合标准,认为各站的最优模型构建合理。
4.3 指数的验证 以历史干旱事件为研究对象,对比分析12个月时间尺度的SRI1(模型1)、SRI2(模型2)、SRI3(模型3)的评价结果,从而验证了指数的合理性和适用性。SRI1、SRI2、SRI3的计算结果见图3。从图中可以看出,传统指数SRI1与非一致性指数SRI2、SRI3的波动变化与历史记载的干旱年份均较吻合。
1972年的旱灾为滦河流域历史上罕见的大旱,流域内多条河流断流,滦河年径流量仅为多年平均值的44%,导致区域水资源严重短缺,受灾面积高达1907 km2,成灾1567 km2,旱死禾苗为173 km2,干旱面积占耕地面积的80%[28]。在1972年6月至1973年7月期间的14个月内,根据12个月时间尺度的SRI1指数计算结果,均属于中度干旱;而在这期间,根据12个月时间尺度的SRI2的计算结果,1972年12月与1973年6月均为重旱,值分别为-1.9、-1.5,且1972年12月接近于极度干旱,分别反映出了1972年全年与1972年6月至1973年6月的干旱情况,与实际较为接近;根据12个月时间尺度的SRI3的计算结果,1972年12月SRI3值为-2.1,为特旱,反映出1972年全年的干旱情况,与实际情况更加接近。

表5 潘家口水库流域各水文站12月份的12个月时间尺度的累计径流量的最优模型参数

图3 典型站波罗诺站1960—2011年12个月时间尺度的逐月标准化径流指数
1980—1984年间,滦河流域各地均出现长时期降水不足的现象,致使干旱灾害大范围连续发生,旱情较为严重,给流域农业生产和民居正常生活都带来严重影响[20]。在这一时期,12个月时间尺度的SRI1计算的结果在1981年10月至1982年6月为重度干旱,其余时段均为中度干旱;12个月时间尺度的SRI2计算的结果在1980年12月,1981年9、10月,1982年6、9月,1983年9、11月,1984年7、9、10、12月均为重旱;SRI3计算的结果在1981年10、12月,1983年9月,1984年7、10、12月均为重旱。SRI2与SRI3计算的结果能够反映出整个时期的干旱较为严重,与实际更加接近。
4.4 干旱特征分析 本文分别以波罗诺水文站12个月时间尺度的SRI1、SRI2、SRI3的干旱等级评价结果为基础,将整个研究期划分为1960—1972、1973—1985、1986—1998、1999—2011年时间长度比较均匀的4个阶段,排除时间长度不同造成的干扰,分别计算4个时间段的各级水文干旱等级频率,从而比较SRI1、SRI2、SRI3在不同时间段的干旱等级频率的变化过程。计算结果见图4。
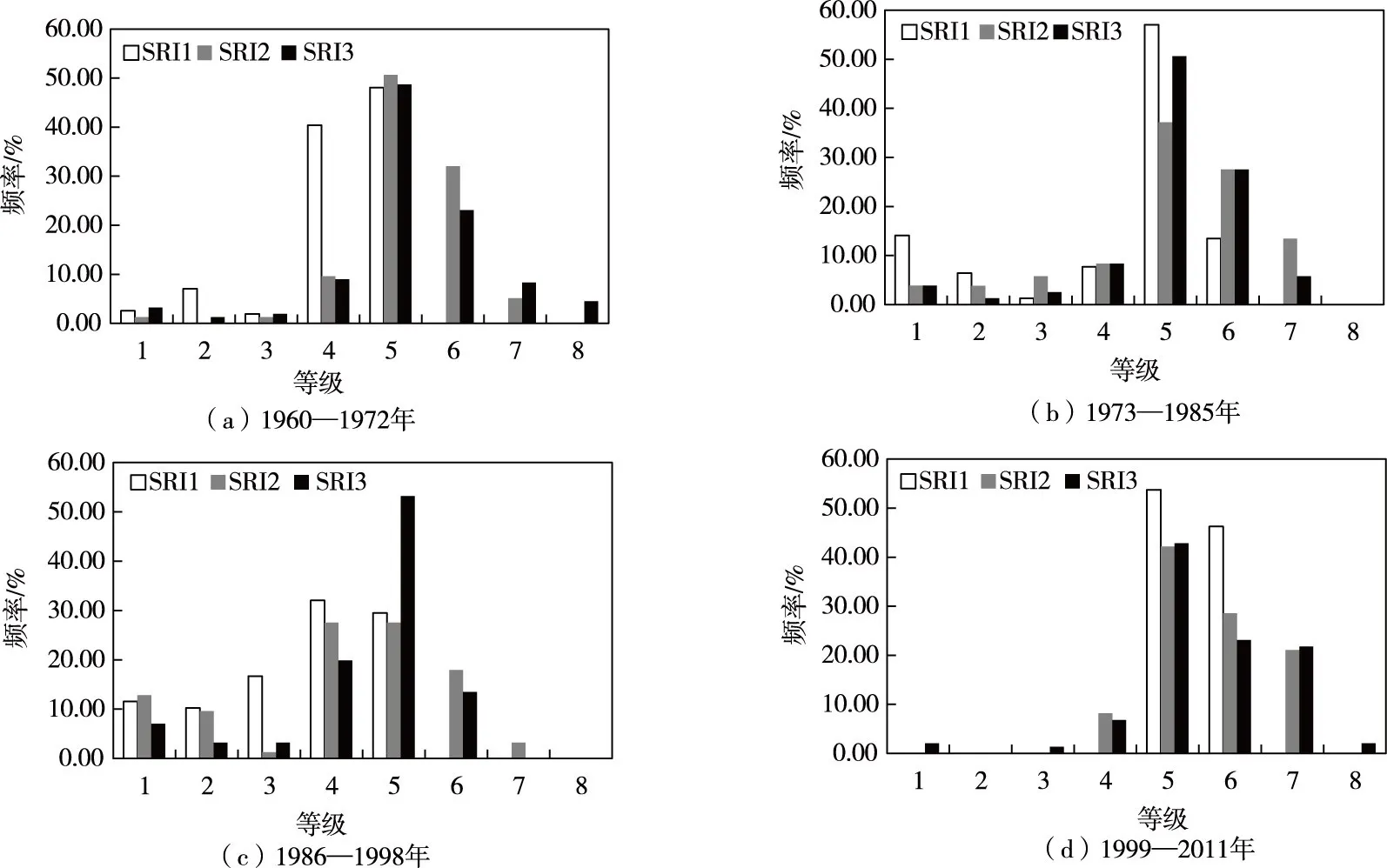
图4 波罗诺站12个月时间尺度的SRI1、SRI2与SRI3在4个时间段的水文干旱等级频率
由图4可知,(a)时段,在轻微干旱至极度干旱情况下(等级5~8级),SRI1、SRI2与SRI3对应的频率分别为48.08%、87.82%、84.62%,可以看出,SRI2与SRI3均比SRI1的频率高,而在极端湿润至正常情况下(1~4级),结果则相反。说明SRI2与SRI3计算的干旱程度比SRI1严重;在(b)时段,频率的变化规律与前一个时间段(a)基本相同;在(c)时段,基于SRI1的等级主要集中于极度湿润至轻微干旱的情况(1~5级),而基于SRI2与SRI3的干旱等级主要发生于正常至中等干旱的情况(4~6级);在(d)时段,基于SRI1的干旱等级全部分布在轻微至中等干旱(5~6级),而SRI2与SRI3的干旱等级主要发生于轻微至重度干旱(5~8级)的情况,对应的频率分别为91.84%、89.8%。(c)与(d)时段也表现为SRI2与SRI3的干旱程度比SRI计算的更加严重。
总结以上分析,4个时间段在整体上均表现为SRI3与SRI2计算得到的干旱程度比SRI1严重,并且随着时间的发展,3个指数计算得到的干旱情况在整体上均趋向于加重,主要原因是在非一致性模型中,以时间t为协变量能够反映出变化环境下径流序列变化的趋势,该趋势是影响径流的一系列因素共同导致的,如气候变化,人类活动等。而在受这些因素的影响下,潘家口水库流域的水文干旱事件频率增加,严重程度增强。
图5展现出了波罗诺站12个月时间尺度的逐月累计径流序列对应的干旱等级。可以看出,使用传统的SRI1计算得到的干旱等级只与累计径流量有关,一定范围的径流量对应一定的干旱等级,而SRI2与SRI3计算得到的干旱等级不只与累计径流量有关,还与时间有关,同一个径流量值因为发生时间的不同,可以对应几个干旱等级。例如,25×106~68×106m3范围内的径流量,根据SRI1指数,得到干旱等级均为轻度干旱,而根据SRI2、SRI3指数,计算得到的干旱等级均有5种,分别是无旱、轻旱、中旱、重旱、特旱。此外,3个指数SRI3、SRI2与SRI1在5~8级干旱中分布的干旱事件依次减少。以上分析证明了在变化环境下,研究区域的径流序列发生了显著的非一致性变化以及干旱指数构建中考虑非一致性的必要性。

图5 波罗诺站12个月时间尺度的逐月累计径流序列干旱等级统计
5 结论
本文以传统的标准化径流指数SRI的计算原理为基础,基于以时间为协变量的非一致性模型构建了时变标准化径流指数SRIt,得出以下结论:(1)在受气候与人类活动影响较大的背景环境下,1960—2011年间,潘家口水库流域的9个水文站,除沟台子站与韩家营站以外,其余站点的径流序列呈显著下降趋势,即存在显著的非一致性特征。(2)基于全局拟合偏差GD、AIC准则和SBC准则计算出最优模型参数。结果表明,径流序列非一致性特征不显著时,对应的最优模型参数均为常数,而当径流序列存在非一致性特征时,对应的最优模型参数为时间t的函数。以波罗诺站的径流序列(存在非一致性特征)为例,比较一致性模型(模型1),一个参数μ随时间变化的非一致性模型(模型2),两个参数μ、σ均随时间变化的非一致性模型(模型3)。结果表明,模型3的GD、AIC和SBC值整体上最小,其次为模型2。通过分位数灰度图可以看出,模型3更能捕捉到径流序列的变化情况,模拟效果更好,从而验证了在非一致情况下,假设Gamma分布参数随时间变化的合理性。(3)以历史干旱事件为研究对象,对比分析波罗诺站3个指数的评价结果。结果表明,在变化环境下,SRI3最能反映出实际的干旱情况,验证了时变标准化径流指数构建的合理性与必要性。(4)随着时间的发展,SRI1与SRIt指数表示的干旱情况在整体上均趋向于加重,且在同一时间段内,SRIt比SRI1表示的干旱情况整体上更加严重,这与Mann-Kendall非一致分析中得出的径流序列存在显著下降趋势相对应。此外,在时变矩模型中,同一范围内的径流量随时间的变化可能对应不同的干旱等级。
为了降低非一致性模型计算的复杂程度,本文选择较为简单的Gamma分布作为径流序列的理论分布线型。然而,模型的分布函数有多种选择,如Lognormal分布、Pearson-Ⅲ型分布等,后续研究可通过模拟优选出最优的分布函数,进一步提高SRIt指数的适用性。

