基于SBFEM的面板坝与可压缩库水动力耦合弹塑性分析方法

许 贺 ，邹德高 ，孔宪京 ，刘京茂

（1.大连理工大学 海岸与近海工程国家重点实验室，辽宁 大连 116024；2.大连理工大学 水利工程学院，辽宁 大连 116024）

1 研究背景

比例边界有限元方法（SBFEM）是一种近年新兴起来的半解析的数值技术［1］，其集成了有限元法和边界元法各自的优势。因此，SBFEM既适用于有限域分析，例如断裂问题［2-3］、饱和土液化分析［4］、跨尺度分析［5-7］、磁电或压电材料分析［8］等；又适用于无限域分析，例如结构与地基相互作用［9］和坝-水相互作用［10-14］等。采用比例边界有限元法模拟库水，可建立一种高效的坝前动水压力计算模型［10］，即直接离散坝水交界面来模拟半无限域库水，不但将该问题的求解维数降低一维，而且自动满足流体域无穷远处的辐射条件。该动水压力计算模型可考虑库水可压缩性、地震激励方向和库底淤沙的波能吸收效应等因素。由于动水压力对于大坝抗震安全评估的重要性，地震荷载条件下作用于坝面上的动水压力问题在试验分析与数值计算方面一直备受关注［15-21］。在坝-库水动力相互作用分析中，库水可压缩性是一个重要的影响因素与研究热点［19-21］。Saini等［19］采用有限元法对重力坝进行了频域动力流固耦合分析，其结果表明，在坝-库耦合系统的基频附近，忽略库水可压缩性可使坝顶动位移产生超过30%的误差。Porter等［20］研究了动水压力对拱坝动力响应的影响，结果显示，在坝-库耦合系统的基频附近，不考虑库水可压缩性时，坝顶加速度响应的误差高达40%以上。以往的研究表明，数值分析时忽略库水可压缩性可能对坝体动力响应造成明显的误差，不利于合理评价大坝的抗震性能，因此，进行坝-库水动力相互作用分析时，需要考虑库水可压缩性。

当采用SBFEM离散坝前半无限域可压缩库水时，需要首先进行一系列离散的动水压力频域求解，再经过傅里叶逆变换将频域解转化为动水压力时域脉冲响应函数，方可计算时域的动水压力。但是，在时域计算前的预备工作中，动水压力频域求解会消耗许多时间。本文建立基于SBFEM的面板坝（CFRD）与可压缩库水动力耦合弹塑性分析方法，在此基础上，为了减少频域求解的计算量，对动水压力计算过程进行简化处理，并且验证该简化方案的精度和效率。

2 计算方法及其简化方案

弹塑性面板坝采用有限元方法（FEM）离散，坝前可压缩库水的动水压力采用基于SBFEM的计算模型。现将坝前动水压力计算方法［10］、本文建立的面板坝与库水动力耦合弹塑性分析方法以及动水压力计算的简化方案介绍如下。

2.1 基于SBFEM的坝前动水压力计算方法 假定库水为可压缩、小扰动理想流体，地震荷载下，坝前动水压力满足方程：

忽略库水自由表面微幅重力波：

坝水交界面上的边界条件：

库底和岸坡迎水面上的边界条件：

由于采用SBFEM离散了坝前半无限域库水，库尾无穷远处的辐射条件自动满足。

图1 坝前库水单元比例边界坐标

如图1所示，根据比例边界有限元的离散方式，将相似中心O置于水库下游无限远处，如此可将利用二维离散网格来模拟三维半无限域库水，直接利用坝水交界面上坝体的有限元网格生成一些由坝面（ξ=0）延伸至库水上游无穷远处的（ξ=+∞）柱状水体单元（ξ为解析求解的径向坐标）。整体坐标（X，Y，Z）和局部坐标（ξ，η，ζ）之间的比例边界坐标变换为：

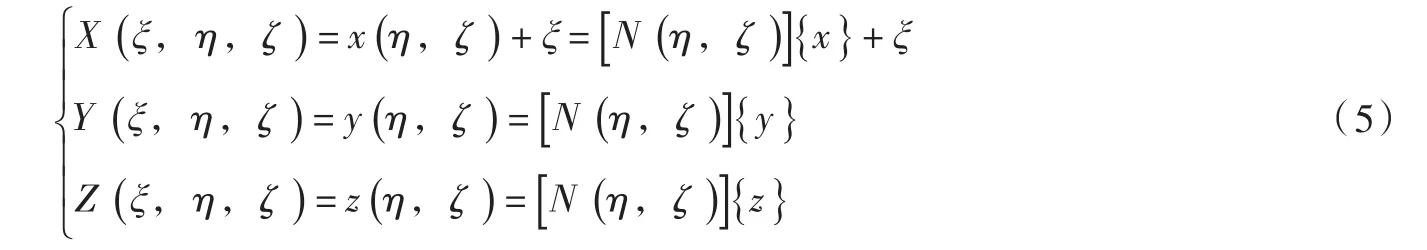
对以上动水压力的控制方程和边界条件通过比例边界坐标变换和加权余量法求解，可以得到频域动水压力控制方程（关于ξ的二阶线性常微分方程）和边界条件，分别如下式所示：

联立式（6）和式（7），将其转化为特征值问题［9］，解得频域坝前（ξ=0）动水压力为：

其中：

2.2 时域面板坝与库水动力耦合计算方法 坝前时域动水压力可由频域解通过傅里叶逆变换计算而得：

其中：

根据积分变换理论中的卷积定理，由式（10）可推得式（12），即时域动水压力是通过时域单位脉冲响应函数（见式（13））与坝水交界面传递而来的时域加速度卷积而得的。

程相关，因此它在tm时刻是可通过卷积计算出的已知量。

考虑地震惯性力输入，在tm时刻坝-库水相互作用系统的运动方程为：

将式（15）代入式（16），进一步整理得：

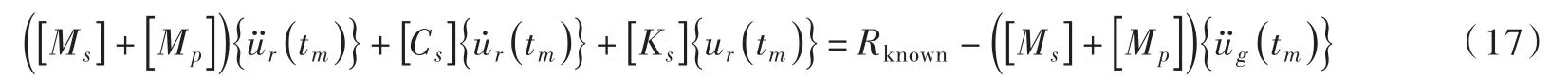
由式（17）可知，在该强耦合计算方法中，只需将附加质量阵［Mp］引入到坝体系统，即可实现坝与库水系统的分区求解，而且不需要两个系统之间的迭代计算过程，因此该方法具有高效的优势。该时域耦合方法可考虑坝体非线性，弹塑性面板坝与库水系统动力流固耦合计算流程如图2所示。

图2 坝与库水动力耦合计算流程

2.3 动水压力计算方法的简化方案 本文选取地震条件下坝体动力计算的常用时间步0.01 s，则动水压力频域求解的频率ω范围为0～100π。一方面，地震动的卓越频率范围为0～20π（0～10 Hz）；另一方面，坝体动力响应的高阶（高频）成分可能很有限。因此，实际计算时，库水动水压力的高频地震响应的贡献可能并不大。若可以缩小频率求解范围、截断高频部分，则可相应地降低计算量。设动水压力频域求解的截断频率为ωT（ωT≤100π），则相应的频域求解范围调整为0～ωT。

仅需改动上述求解动水压力单位脉冲响应函数{hp(t)}具体流程中的第（2）步，即可改进动水压力计算方法，提高计算效率，进而实现该动力耦合计算方法的化简：当0≤ωi≤ωT时，通过式（11）计算每个频率点上的动水压力频域响应函数当ωT＜ωi≤100π时，取（零矩阵）。

在保证较高计算精度的前提下，确定ωT的取值以尽可能多的节省计算量是该简化方案的关键点。本文基于面板坝的非线性动力流固耦合分析，对截断频率为ωT的取值进行了敏感性分析，以下算例的截断频率ωT分别取为10π、20π、30π、40π、50π、100π（未截断）。

3 面板坝算例验证与分析

采用大连理工大学工程抗震研究所自行研发的岩土工程非线性有限元（与比例边界有限元）程序GEODYNA［22］对典型的面板坝与可压缩库水进行动力流固耦合验证计算，通过比较截断频率ωT对坝前动水压力分布规律和面板应力极值（最大值）及其分布的影响，建议了不同坝高时，截断频率ωT的取值，且分析了相应的取值依据。

3.1 大坝有限元模型与地震动输入 采用4种不同坝高H（50 m、100 m、200 m、300 m）的规则面板堆石坝作为计算模型，其有限元网格如图3所示。面板坝的上、下游面坡度均为1∶1.4和1∶1.6，梯形河谷两岸坡度均为1∶1，其他参数详见表1。库水网格由坝体迎水面的有限元网格直接生成，如图4所示。假定面板堆石坝坐落在刚性地基上（地震采用一致输入法），采用一组《水工建筑物抗震设计规范》中的规范谱生成的人工地震波和一组Koyna实测地震波进行计算，地震波时程如图5和6所示，两组地震波顺河向和竖向的加速度峰值分别为1.5 m/s2和1.0 m/s2。

3.2 本构模型及参数 土体的静、动力本构关系具有非线性特点［23-27］，本文筑坝堆石料采用广义塑性本构模型［23］，该模型可合理地反应堆石料的材料非线性和高围压条件下的颗粒破碎等特性，17个参数取值见表2。面板与垫层之间的接触面采用理想弹塑性模型，参数选取如表3所示。混凝土面板采用线弹性模型，弹性模量E=30 GPa，泊松比ν=0.167。竖缝和周边缝单元［28］的法向压缩与拉伸刚度分别为25 GPa/m和5 MPa/m，切向刚度为1 MPa/m。水中波速c=1440 m/s，水体密度ρ=1.0 g/cm3，库底和岸坡入射波的反射系数α=0.6。

图3 面板坝有限元网格

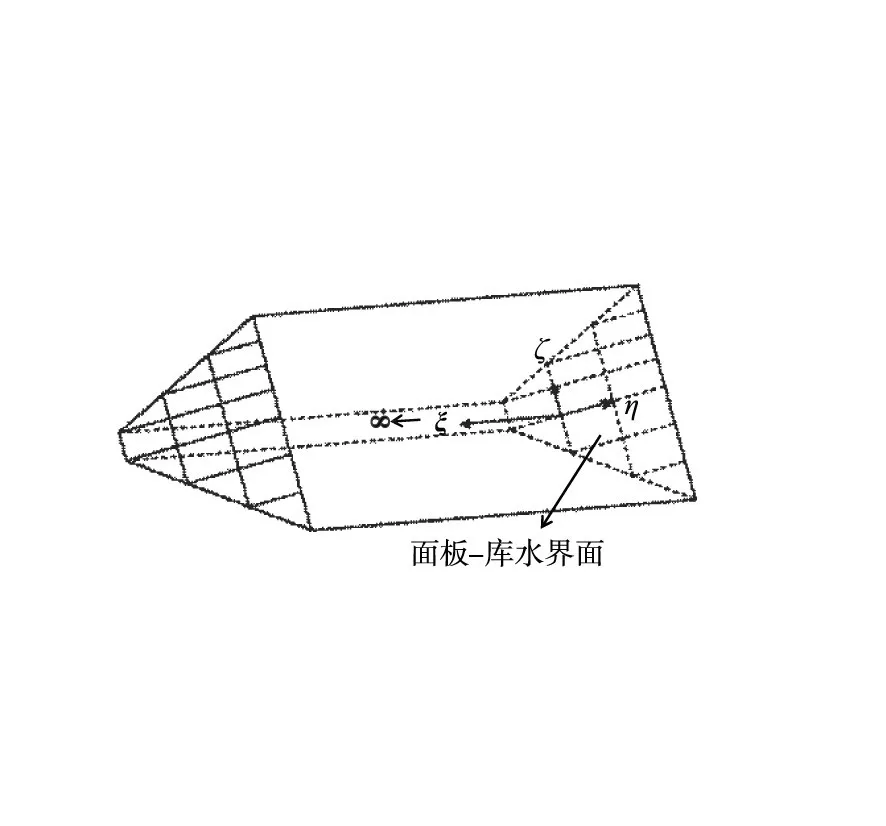
图4 库水网格示意

3.3 动水压力分布规律 以迎水面中线的动水压力绝对值包络为例说明分布规律。在Koyna地震作用下，100 m和300 m坝高面板坝的动水压力分布见图7，图8为50 m和200 m高的面板坝在人工地震波作用下的动水压力分布。可见，随着截断频率减小，坝前动水压力逐渐减小（精度降低），但动水压力分布保持相似的形状；坝高越低，动水压力随着截断频率减小而降低的幅度就越显著；当30π≤ωT≤50π时，动水压力的误差很小；当ωT≤20π时，动水压力的误差则相对明显。

图5 人工地震波时程

图6 Koyna地震波时程

表1 大坝有限元网格参数

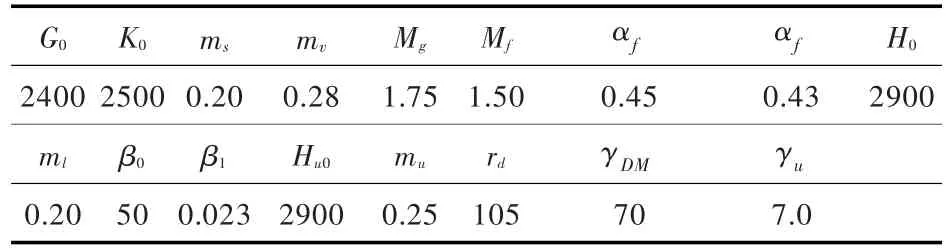
表2 堆石料广义塑性模型参数

表3 理想弹塑性接触面模型参数

图7 坝面中线动水压力包络（Koyna地震波）

图8 坝面中线动水压力包络（人工地震波）

3.4 面板动应力分析 混凝土面板作为核心防渗体，对面板坝的安全运行起着至关重要的作用［29］。通过对比面板动应力极值及其分布差异，分析截断频率（10π，20π，30π，40π，50π，100π）对面板动应力计算精度的影响。以下计算面板动应力的误差时，以截断频率ωT=100π（未截断）的结果为基准。

表4 面板动应力极值（坝高50m，人工地震波）

表5 面板动应力极值（坝高200m，人工地震波）

表6 面板动应力极值（坝高100m，Koyna地震波）

表7 面板动应力极值（坝高300m，Koyna地震波）

表4和表5分别为坝高50 m和200 m的面板坝在人工地震波作用下，面板动应力极值（最大值）结果；表6和表7分别为坝高100 m和300 m的面板坝在Koyna地震波作用下，面板动应力极值结果。表8—表11分别为相应的面板动应力极值的最大误差，可见，在不同坝高条件下，随着截断频率减小，面板动应力的误差逐渐增大；当截断频率较小时（ωT≤30π），随着坝高增大，面板动应力极值的误差会减小，这主要是由于坝越高其基频越低，截断频率可适当减小。

图9为坝高50 m的面板坝在人工地震波作用下，面板坝轴向压应力的极值分布情况；图10为坝高300 m面板坝在Koyna地震波作用下，面板顺坡向拉应力极值分布。可见，随着截断频率的减小，较低坝的面板高应力区范围变化更明显，这主要是由于低坝的基频较高，对截断频率的降低比较敏感。

表8 面板动应力极值的最大误差（坝高50m，人工地震波）

表9 面板动应力极值最大误差（坝高200m，人工地震波）

表10 面板动应力极值的最大误差（坝高100m，Koyna地震波）

表11 面板动应力极值的最大误差（坝高300m，Koyna地震波）

表12 截断频率及相应计算效率

图9 坝轴向压应力极值分布（坝高50m，人工地震波）

图10 顺坡向拉应力极值分布（坝高300m，koyna地震波）

由以上分析可知，随着面板坝高度H增加，可相应地降低截断频率ωT，仍然保持具有较高计算精度，更多地节省频域求解的计算量。根据计算结果的分析给出以下建议：当100 m＞H≥50 m时，取ωT=40π；当200 m＞H≥100 m时，取ωT=30π；当H≥200 m时，取ωT=20π。根据建议，表12列出了相应计算效率的提高程度（以ωT=100π为基准），面板坝越高，则计算效率提高的越多。

4 结论

本文在面板坝与可压缩库水动力流固耦合时域分析方面开展了研究：（1）采用SBFEM模拟坝前库水，并且将其与FEM离散的面板坝耦合，进而建立了面板坝与可压缩库水动力耦合弹塑性分析方法，并根据坝与库水动力耦合响应的特点，对动水压力计算过程进行了简化处理，仅需确定截断频率ωT，即可大幅度地降低动水压力频域求解的计算量，还可保证较高的计算精度。（2）地震的卓越频率在较低的范围内（0～10 Hz），而且地震条件下坝体动力响应的高阶（高频）成分对动水压力的影响也有限。因此，库水的高频地震响应贡献并不大，可截断高频部分减少计算量。（3）随着截断频率ωT减小，坝前动水压力逐渐减小（误差增大），但动水压力分布保持相似的形状；坝高越低，动水压力随着截断频率减小而降低的幅度就越显著。在不同坝高条件下，随着截断频率减小，面板动应力的误差逐渐增大。当截断频率较小时（ωT≤30π）可发现明显的规律，即随着坝高增大，面板动应力极值的误差会减小；这主要是由于坝越高其基频越低，截断频率可适当减小。（4）根据计算结果分析给出以下建议：当100 m＞H≥50 m时，取ωT=40π；当200 m＞H≥100 m时，取ωT=30π；当H≥200 m时，取ωT=20π。面板坝越高，则计算效率提高的越多。

本文建立的面板坝与可压缩库水动力耦合分析方法以及动水压力计算的简化方案，也适用于混凝土坝的动力计算。