基于改进降水输入模块的融雪径流模拟：以拉萨河为例

刘江涛 ，徐宗学 ，赵 焕 ，彭定志

（1.北京师范大学 水科学研究院，北京 100875；2.城市水循环与海绵城市技术北京市重点实验室，北京 100875）

1 研究背景

积雪在地球的物质循环和水量平衡中扮演着十分重要的角色，积雪能够增加地表反照率，影响能量的收支平衡［1-2］。积雪融化产生的融雪径流是包括黄河、长江和雅鲁藏布江在内的众多河流的主要补给源，为下游数以亿计人民的生产和生活提供十分重要的支撑作用。在全球变暖背景下，全球范围内积雪正在逐渐融化［3］。尤其是在北半球的中高纬度地区，积雪融水的变化更易给当地的生态环境和生产生活带来影响，雪消融会引发洪涝及泥石流等自然灾害［4］。因此，研究融雪径流动态变化尤其是在融雪期的变化对高原河流流经地区的水资源持续利用和防灾减灾具有十分重要的现实意义［5］。

融雪径流的模拟主要有基于物理机制的能量平衡法和度日因子法，基于物理机制的模型能够反映流域中积雪在消融过程中能量的动态变化特征，比如积雪表面所接受到的长波辐射、短波辐射以及积雪内部的热通量交换等能量变化细节［6］。基于物理机制的模型有SHE模型［7］、PRMS模型［8］、VIC模型［9］等，它们在众多的冰雪覆盖区得到了广泛的应用［10-12］。然而，基于物理机制的模型所需的数据较多，我国的西部高寒地区，气象站点分布极度稀缺，水文气象数据无论是在数量上还是时间序列的长度上都较难满足模型的输入需求。度日因子模型假设融雪量与气温存在线性关系，模型的结构简单，所需的数据容易获得，并且模拟的结果较为理想。常见的度日因子模型有SRM模型［13］、HBV模型［14］、WetSpa模型［15］等，国内外研究学者利用度日因子模型或改进的度日因子模型在融雪过程模拟中开展了广泛的研究。李兰海等［16］利用APHRODITE驱动SRM模型在开都河流域进行研究，认为有效活动积温改进的度日数能够提高模型中融雪速率和径流系数的计算精度。Immerzeel等［5］在融雪模型中增加冰川模块，以喜马拉雅山流域为研究区，分析了流域内的积雪变化，并对冰川融水进行了模拟，认为在模拟期冰川融化逐渐加速，对印度河流域的水文循环产生了影响。综合众多研究，度日因子模型能够在高寒山区具有很好的适用性，且模型计算易于实现，结构易于与其他模块耦合，被广泛的应用于冰雪消融及冰雪融水径流模拟研究中［6］。

在青藏高原地区，气象站点往往设立在低海拔便利地区，空间分布十分不均，很难从地面站点中获得流域气象要素时空分布的真实情况。气象卫星能够提供高时空分辨率的气象要素反演产品，对气象站点覆盖空白地区能够起到很好的补充作用，在过去的十几年中得到了较为广泛的应用［17-20］。然而，气象卫星数据在影像获取和数据处理过程中存在较多不确定性，在某些区域的适用性可能相对较差，因此在区域中使用气象卫星数据前，应对卫星产品的精度进行评估，并对数据精度进行校正，可以有效降低卫星产品的系统误差，提高卫星数据产品的质量。降水卫星精度校正过程中常使用的方法包括逐步订正［27］、最优内插［28］、概率密度匹配法［21］和线性模型［22］等，孙乐强等［23］采用逐步订正和最优插值两种方法提高TMPA卫星数据对站点降水量的反演精度，但是该校正方法只使用了最简单的降水径流系数法进行模拟验证，没有与较为成熟的融雪径流模型进行耦合，且该方法在校正的权重函数选择中只考虑卫星降水网格与站点之间的距离关系，没有考虑地形因素对权重函数的影响，使其在海拔变化剧烈的半干旱的高寒地区的应用可能存在一定的局限性。

本文通过改进逐步订正法，构建降水输入模块，并将其与较为广泛应用的融雪径流模型（SRM）进行耦合，使其具备校正高寒地区降水数据精度并形成半网格半站点的降水输入特点，以期提高融雪模型中降水产流项的模拟效果，使模型更加准确地模拟融雪径流的变化情况。并以拉萨河流域为研究区，构建改进后的融雪模型，通过与原模型的精度进行对比，验证改进后模型的适用性，为半干旱高寒区水资源分配及管理提供有用的信息。

2 模型构建

2.1 度日因子模型介绍 对高寒地区而言，选择合适的模型对融雪过程进行模拟是影响融雪径流模拟效果的关键。度日因子模型是基于冰雪消融与正积温之间的线性关系所建立的［6］，Snowmelt Runoff Model（SRM）是一种概念性度日因子模型，已在29个国家、100多个流域得到了广泛应用［13，24］。SRM模型计算日融雪径流的原理是将当日融雪量和降水量叠加到前日径流退水量上。SRM模型在各个高程分区上降水数值是基于参考气象站点的数据，利用降水递减率进行推求，而流域地形特征对降水时空分布产生的差异不予考虑［25］。因此，本文在采用SRM模型中产流模块的基础上，耦合考虑地形因子的逐步订正法的降水模块。度日因子模型需要输入的变量包括日气温、日降水以及日雪盖数据等，产流计算方法如下［26］：

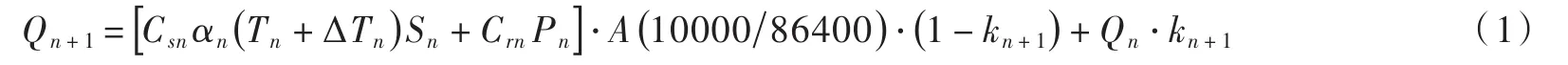
式中：Qn+1为第n+1天的流量，m3/s；Csn为融雪径流系数；αn为第n天的度日因子，cm·℃-1·d-1； Tn为度日数，℃·d；ΔTn为由气温直减率得出的度日修正值，℃·d；Sn为积雪覆盖率；Crn为降雨径流系数；Pn为第n天的降雨量，cm；A为流域面积，km2；kn+1为第n+1天的径流衰退系数。

按照融雪模型中径流产生的来源，式（1）可以被简化为如下形式：

式中：Sn为每天新产生融雪产生的流量，m3/s；Rn为每天新产生的降水产生的流量，m3/s；QSn为第n天实测径流中由融雪产生的部分，m3/s，QRn为第n天实测径流中由降水产生的部分，m3/s。

当流域海拔高程超过500 m时，需要对流域进行分区处理，此时降水产流项公式为：

式中：R为流域中降雨的产流量，m3/s；Ri为第i个分区降雨的产流量，m3/s；Crni为第i个分区的退水系数；Pi为第i个分区的降雨量，cm；Ai为第i个分区的面积，km2；N表示分区总数。

2.2 降水输入模块原理 在青藏高原的高寒地区，山区的海拔变化和地形起伏变化幅度均比较大，气象站点一般建设在低海拔的平原地区，而在高海拔地区无气象站点覆盖。各高程带上的降水量大小通常使用降水递减率进行推算［25］，这样会忽略区域中地形及水汽分布对降水的影响。气象卫星数据是无资料或缺资料地区气象数据的重要补充，可以有效克服气象站点时空分布极度不均问题，但是在半干旱高寒区域使用时应该对其精度进行校正，使之更加符合区域降水的实际情况。

逐步订正法在降雨卫星数据校正过程中使用权重函数来确定降水场各个格点所分配的残差系数，但当前研究中，大多仅考虑网格各个位置处的数据与地面站点数据的空间关系，而没有考虑地形因素对校正过程所带来的影响，因而在海拔变化幅度巨大的青藏高原地区的适用性可能相对较差。本文在降水输入模块中考虑地形因子影响，改进了逐步订正法［23，27-30］对降水卫星数据的精度进行校正，在选用距离权重时考虑地形因素对校正结果的影响，并与广泛应用的融雪模型进行耦合。本文对降水输入模块进行改进的过程为：首先，以原始降水卫星网格数据作为模块的初始降水场，将初始场中实测站点位置处的卫星数据降水量与实测降水量之间的差值通过权重函数插值到初始场网格的各个格点位置处，从而得到第一猜测场；然后，将第一猜测场作为初始场，重复上述步骤，最终得到较符合地面真实降水情况的降水网格数据；最后，将网格数据与地面实测数据按照高程分带的不同进行组合（当高程分带的海拔高度大于气象站点平均海拔高度时，高程带使用校正后的降水卫星数据，反之则使用地面站点的降水数据），输入到融雪模型中，模拟研究区的融雪径流情况。具体计算步骤如下：

（1）待校正的初始场确定。待校正的初始场降水数据是从降水卫星数据中提取，本文首先确定研究区域的矩形范围［L，W］，此范围内的降水卫星网格数据即为待校正的初始场Γ0。在对降水场进行校正时，地面气象站点的位置与降水网格节点位置可能不相匹配，本文使用双线性插值法推求站点位置处的降水卫星数据。

（2）降水输入模块中降水场的校正。降水输入模块得到降水初始场Γ0，其中第k个地面站点的实测值Mk与在初始场中的该点位置处的数值Γ0k的差值，通过权重函数对初始场进行订正得到第一猜测场Γ1，并将第一猜测场作为初始场重复上述步骤，直到订正后的场的数值逼近观测值：

式中：Γab1为在第一猜测场的格点坐标（a，b）位置处的第一猜测值，mm；Γab0为在初始场的格点坐标（a，b）位置处上的初始值，mm；Mk为站点k上的实测值，mm；Γab0k为初始场中在站点k位置处的卫星数据初始值，mm；Wabk为权重因子，它的数值范围为0～1；K为搜索半径中的站点数（图1）。

图1 降水输入模块中逐步订正法

（3）降水输入模块中权重函数的确定。权重函数Wabk有圆形、椭圆形和曲率椭圆形等不同的形式。本文选用比较常用的圆形权重函数［23］。

式中，R为搜索长度，降水输入模块的搜索长度的初始值为0.5°，在模型中会以0.5°为迭代步长，增加至区域边界的范围最大值，降水输入模块最后选择校正效果最好的步长作为模块最终使用的搜索长度；dabk为格点（a，b）到地面站点k的距离，m。

（4）地形因子修正。青藏高原地区地形复杂，海拔的高度变化幅度大，因此在订正过程中应该考虑地形因素对订正效果的影响。降水输入模块中地形因子为：

式中：Vabk为地形因子，mm；Dab为格点（a，b）位置处的海拔高度数值，m；hk为站点k位置处的海拔高度，m；α为地形修正系数，mm/m，其数值与地形、植被覆盖、水汽梯度等因素有关，本文根据参考文献［31］的研究结果选择α的值为0.005 mm/m。

此时考虑地形因素影响的逐步订正公式（4）可以修改为：

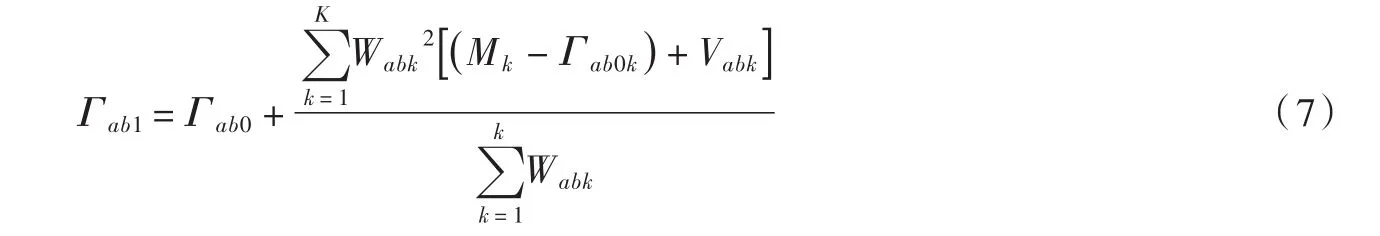
2.3 降水输入模块与融雪径流模型耦合 高寒区径流的来源一般可以分为两部分，一部分是累积在地表面的积雪在温度变暖的时候由消融产生的融水，另一部分是降水经过下渗蒸发拦截等过程形成的降水径流。本文积雪信息是通过MODIS卫星数据获得，降水信息通过TRMM卫星数据和地面降水数据获得。采用改进的逐步订正法对降水卫星数据进行校正后，降水卫星数据的反演精度在一定程度得到提高，但与地面站点的“真实”值相比仍具有一定的差距。因此在降水输入模块中会对校正后的降水卫星数据与地面站点数据进行组合，被地面站点所覆盖到的高程带分区应使用地面站点数据，无法被地面站点覆盖到的分区使用校正后的卫星数据。模型耦合具体流程如图2所示。

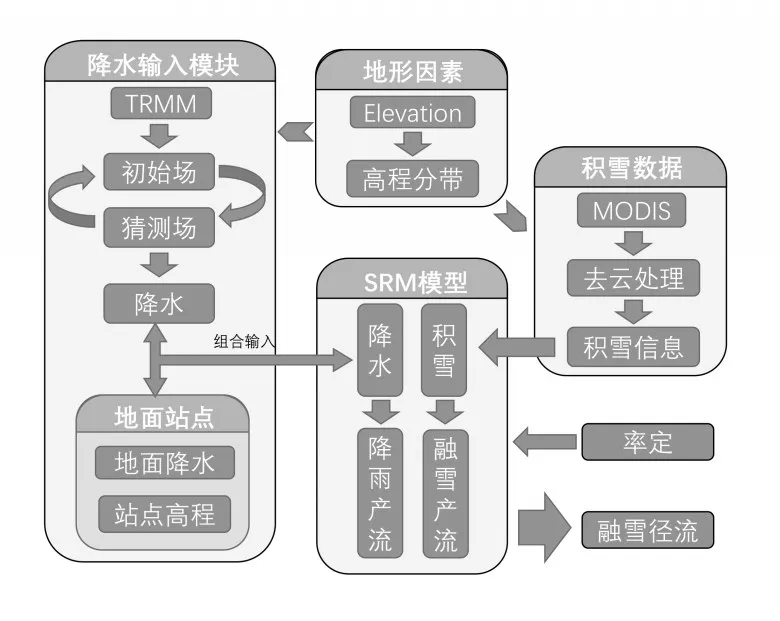
图2 融雪径流模型与降水输入模块耦合

图3 累积面积与高程曲线

首先，融雪模型将流域每500 m划分一个高程带单元，通过累积面积与高程曲线图（图3）得到各个分带的平均高程（单位m），同时计算流域内所有气象站点的平均高程（单位m）。具体而言，流域内逐点的高程值集合其中N表示高程点个数，流域中最小高程值为hmim，最大高程值为hmax，按照每500 m一个高程分区对流域进行分带处理，得到N个高程分区，其中（INTup表示向上取整）。对于第i个高程分区Zonei，其高程的最低点为hi_min，高程的最高点为hi_max。则此时的Elvi应该满足：式中 f()x表示累积面积高程曲线的拟合方程，Ai表示第i个分区的面积变量，Ai1和Ai2分别表示第i个高程分区最低点高程所对应的累积面积和最高点高程对应的累积面积。Elvi表示第i个高程分区的平均高程。

融雪模型计算融雪径流的原理是将每日的融雪量与降水量叠加到前日的径流退水量中。每个分区的融雪量由度日因子进行计算，每个分区的降水量由地面站点数据和降水卫星数据进行计算。对于第i个分区Zonei的降水输入项Pi，其数值为：

降水模块判断每个分区的平均高程Elvi与气象站点平均高程的大小关系。分别选用地面站点数据或降水卫星数据（图4）。若≤Elvi，则该分区的降水数据使用校正后的降水卫星数据PTrmm，若＞Elvi，则该分区的降水数据使用地面站点数据PSta。

3 应用案例

图4 不同高程带对应不同的降雨数据源

3.1 研究区概况 雅鲁藏布江位于青藏高原的西南部，海拔范围大，气象站点稀少。本文选取雅鲁藏布江流域中的拉萨河流域作为研究区（图5），拉萨河流域面积为3.18×105km2，拉萨河流域的气候类型是高原温带半干旱气候类型，多年平均降水量为445 mm，时空分布十分不均匀，表现为从东南到西北地区逐渐递减［32-33］。径流的补给主要来源于雨水、融雪融水和地下水，其中融水补给占到径流总量25%［34］，是雅鲁藏布江径流的重要组成部分。

图5 研究区位置以及气象站点和水文站点分布

3.2 数据来源和处理 本文使用的数据主要包括数字高程（DEM）、积雪覆盖、降水数据等。

3.2.1 数字高程模型（DEM）DEM来源于NASA的“EARTHDATA”平台，数据版本为ASTER Global Digital Elevation Model V002，空间分辨率为30 m，重采样为500 m。拉萨河流域的高程范围为3581～7112m，将DEM按照500 m进行高程带划分，拉萨河流域可以分为7个高程区（如表1）。

表1 拉萨河流域高程分区

3.2.2 MODIS积雪数据 融雪是高寒地区径流的重要来源，但是在人迹罕至的高寒地区，传统的地面观测很难获得区域内积雪的时空分布。MODIS（Moderate-Resolution Imaging Spectroradiometer）产品能够提供多时段不同分辨率的积雪覆盖产品，在积雪研究中发挥着十分重要的作用。本文使用MODIS系列数据中MOD10A1积雪二元值数据，其空间分辨率为500 m，时间分辨率是1 d。从MODIS中获取积雪数据的算法是SNOMAP算法［35］，利用积雪在MODIS的可见光波段具有较强的反射率，而在近红外波段具有较强的吸收能力，通过计算归一化差值积雪指数NDSI来识别积雪：

式中：band4为第四波段（绿光）（0.545～0.565 μm）；band6为第六波段（近红外波段）（1.652～1.680 μm）。

在非林积雪区域，当像元的NDSI≥0.4时，该像元会被定义为雪。由于水体的反射特性和积雪相似，因此利用NDSI识别出的积雪中会存在水体，本文利用MODIS的第2波段band2（0.841～0.876 μm），设置波段阈值去除水体的影响，即设置band2≥0.11的像元为无水体的雪［36-37］。通过时间序列和空间相关性对积雪识别结果进行去云处理［38］，最后得到拉萨河流域多年逐日积雪覆盖率变化曲线（3—12月）（图6）。

为了验证NDSI和去云处理法得到的积雪数据的可靠性，本文将计算得到的积雪覆盖率与“寒区旱区科学数据中心（http：//westdc.westgis.ac.cn/）”的“青藏高原地区MODIS逐日无云积雪产品（2002—2010）”［39］产品在日尺度上进行对比，计算各个分区和流域整体上的相关系数、均方根误差和标准差，结果如表2所示。在流域整体上，本文计算得到的积雪数据与寒旱所的积雪产品之间的相关系数为0.816，均方根误差为0.076，标准差为0.131，因此两套数据在流域整体上的相关性强，偏差小，精度相当。从各个分区来看，相关系数数值最小的分区为G分区，相关系数仅有0.451，但是G分区的面积只占整个流域总面积的0.02%，对积雪产品整体精度影响较小。C、D、E分区的相关系数都在0.76以上，相关性较强，且均方根误差和标准差数值较小，偏差较小，它们的面积占流域总面积的81.10%。因此本文通过NDSI和去云处理所得到的积雪数据与寒区旱区科学数据中心所发布的逐日无积雪产品在精度上相当，数据的可靠性较强，可以进一步进行融雪模拟研究。

表2 积雪数据的可靠性验证

从积雪覆盖率变化曲线（图6）中可以看出，拉萨河流域不同高程分区的积雪覆盖率多年逐日变化趋势是相同的，从积雪覆盖率的逐月变化情况上看，积雪覆盖率总是在4月份达到最大值然后逐月消退，在8月份多年平均积雪覆盖率达到了全年的最低值。因此本文选择4—11月份作为拉萨河流域融雪季进行融雪模拟。从积雪覆盖率的分带情况上看，从A分带到G分带的积雪覆盖率逐渐增加，积雪覆盖率与各个分区的高程值呈现出正相关的关系，即高程分区的高程越高，分带的积雪覆盖率数值越大。

3.2.3 降水数据 降水数据是SRM模型的重要输入变量，降水在各个分区带的精度影响了模型模拟融雪径流的效果。拉萨河流域气象站点的平均海拔高度是3942.80 m，而流域的海拔高度范围是3581～7112 m，在传统的SRM模型中只有A分区具有实测的降水数据，在其他分区中的降水数据一般使用降水递减率推求。降水数值随海拔高度线性变换的处理，忽略了流域中地形、海拔高度以及水汽等因素的影响，使得降水数据出现均坦化的问题［25］。融雪模型与降水输入模块耦合的模型，使用降水卫星数据对气象站点覆盖不到的高程带进行补充。TRMM（Tropical Rainfall Measuring Mission）3B42数据产品的空间分辨率是 0.25°×0.25°，时间分辨率是日，空间范围是50°S～ 50°N，180°W～180°E，TRMM数据相对较高的时间和空间分辨率使其在众多区域上得到了广泛的应用，降水输入模块调用的降水数据包括地面降水站点数据（图5）和TRMM数据，降水数据信息见表3。

图6 拉萨河流域不同高程分区多年平均逐日积雪覆盖率（3—12月）

表3 降水数据的时空分辨率和使用的时间段

为了保证降水输入模块对降水卫星数据校正的可靠性，本文使用的气象站点数据向拉萨河流域外进行了扩展，气象站点使用流域内及流域外的11个站点，站点分布如图5所示。

3.3 模型率定和验证 在模拟中，利用2001—2007年的日流量数据进行率定，利用2008—2014年的日流量数据进行验证，并利用Nash-Sutcliffe系数NSE和百分偏差PBIAS指标对改进的融雪模型精度进行评价［40］：

式中：Qi为实测的日流量，m3/s；Q′i为模拟的日流量，m3/s；为实测的流量平均值，m3/s；n为模拟的天数。

NSE范围为-∞～1，其数值愈接近1，说明模型模拟的精度愈高。当NSE的数值介于0～1之间时，说明模型具有一定的模拟能力，而当NSE的数值小于0时，说明模型对融雪径流不具备模拟能力。

百分偏差的公式如下：

式中，PBIAS的数值愈接近0说明模型的精度愈高。当PBIAS的数值为正时，说明模型低估了融雪流量，当PBIAS的数值为负时，说明模型高估了融雪流量。

4 结果与分析

本文基于积雪数据以及站点和TRMM降水数据，对2001—2014年的拉萨河流域的融雪径流过程进行模拟，其中2001—2007年为率定期，2008—2014年为验证期，得到耦合降水输入模块的融雪模型，以及由此估算得到的融雪流量过程和精度评价结果，并与改进前的融雪模型得出的结果进行对比。

4.1 降水卫星数据校正结果 气象卫星数据具有观测范围广，观测范围连续等特点，能够为气象站点稀缺的高寒地区有效地提供数据上的补充，但是在区域应用前应先对其进行评估和校正。降水输入模块对降水卫星的校正结果如表4所示，从表4可以看出，原始的TRMM降水数据的精度较低，地面站点与站点位置处的TRMM数据的相关系数（CC）为0.307，百分偏差为49.0%，说明在绝大部分时间内TRMM日降水数据反演拉萨河流域的降水效果相对较差。在降水输入模块中，一共进行了5次迭代，即校正步数为5，每经过一次迭代降水输入模块会计算地面站点数据与在站点位置处的卫星数据的相关系数和百分偏差，并将生成的猜测场作为初始场进行重新校正。经过降水输入模块修正的逐步订正法校正后，TRMM降水卫星的精度改善较为明显，相关系数从0.307上升到0.613～0.839，而百分偏差从49.0%下降到0.8%～1.5%。尤其是当校正步数等于4的时候降水卫星对地面降水的反演精度达到最大，此时TRMM降水卫星数据与地面站点数据之间的相关系数为0.839，百分偏差为0.7%。可以看出改进后逐步订正法对卫星的精度提升较大，经过校正后的卫星降水数据通过降水输入模块与地面站点进行组合驱动融雪径流进行模拟。

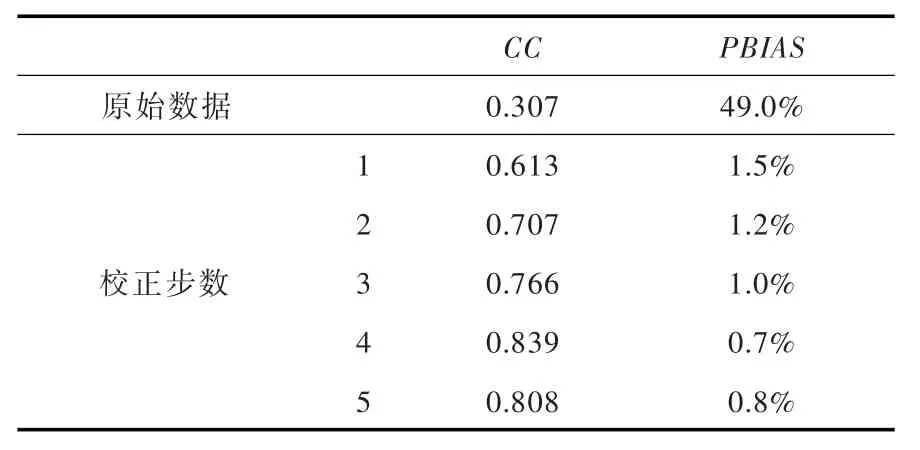
表4 拉萨河流域TRMM降水卫星校正结果

图7 拉萨河流域融雪径流模拟值和实测值

4.2 模型模拟效果评价 本文基于改进的逐步订正法构建了降水输入模块，并将其与融雪模型进行耦合，利用高程分带组合输入半网格半站点的降水输入数据，以拉萨河为例对半干旱高寒区的融雪径流进行了模拟，从图7和表5中可以看出，传统的融雪径流模型和采用耦合降水输入模块的融雪模型模拟值与实测值有很好的拟合效果，能够大体上模拟出融雪径流的实际变化趋势。在率定期2001—2007年，原模型的纳什效率系数NSE和PBIAS分别为0.695和30.3%，改进后的融雪模型的NSE和PBIAS分别为0.741和14.5%。在验证期2008—2014年，原模型的纳什效率系数NSE和PBIAS分别为0.744和22.8%，改进后的融雪模型的NSE和PBIAS分别为0.770和15.4%。改进后的融雪模型提高了NSE的数值和降低了PBIAS数值，减小了相对误差，提高了模拟精度，说明融雪模型降水项改进后的高寒地区的融雪径流过程模拟要优于改进前的模拟效果，更加接近流域的实际产流情况。

在拉萨河流域应用SRM模型和耦合降水输入模块的模型的模拟值和实测值拟合程度较好，它们的变化趋势一致。但无论是原融雪模型还是改进后的模型，对退水的效果模拟都很差，总是在模拟年开始时降到“无水区”，这主要是因为在半干旱高寒地区，冬季和春季的降水相对较少，由降水产生的降水径流相对较少，而此时的温度较低融雪量也相对较少，因此融雪径流总量相对于其他降水充沛和温度偏暖时期径流总量要少的多，更重要的是SRM融雪径流模型中不包含地下水模拟的模块，无法对研究区的基流进行模拟。

5 讨论

度日因子模型是半干旱高寒地区融雪径流模拟的重要工具，模型结构简单，所需的数据较少且易得，因此在融雪过程模拟中得到了广泛的应用。随着遥感产品种类越来越多，精度越来越高，融雪过程的模拟效果也不断增强。但是在融雪径流模拟中仍然存在一系列的不确定性。模型不确定性包括水文模型参数的不确定性和水文模型输入变量的不确定性等内容。对于模型参数而言，在度日模型中会将风吹雪和雪的积累与消融等动态过程进行简化，只使用简单的经验公式或者经验参数代替。对于模型的输入变量，降水和积雪是模型的重要输入变量，青藏高原地区海拔较高，下垫面变化复杂，植被、坡度和坡向等都会对模型的输入变量带来一定的误差。如何减小输入变量的误差，提高融雪径流过程模拟的精度是未来研究的重要方向［43］。

5.1 降水类型对模拟结果影响 降水类型（雨、雪和雨夹雪）会影响融雪径流的模拟精度，不同的降水类型形成径流的过程不同，降雪在冬季累积到地面上，在温度升高时，通过雪的累积和消融过程形成径流。降水直接降到河流中，或经过土壤下渗，蒸散等过程后汇聚到河流中［44］。因此不同的降水类型对融雪径流模拟的影响也是不同的，可以通过分离降水类型来提高青藏高原地区融雪径流过程模拟的精度。在水文模型中，常利用单温度阈值法对降水进行分割，单温度阈值法常设定0℃为临界温度阈值，当温度高于临界温度时，降水的形态为雨；当温度低于临界温度时，降水的形态为雪［45］。单温度阈值法会导致融雪模拟过程存在一定的不确定性，首先，不同降水形态会在-2℃～4℃之间进行转换，即在此温度区间内，雨、雪和雨夹雪均有可能发生，单温度阈值法设定固定的阈值会导致水文模型高估或低估降水量和降雪量［46］。其次，在流域复杂的地形条件下，使用单温度阈值法忽略了下垫面的异质性。双温度阈值法，设定临界最低温度和临界最高温度，当温度高于临界最高温度时，降水的形态为雨；当温度低于临界最低温度时，降水的形态与雪；当温度介于临界最低温度和临界最高温度之间时，降水的形态为雨夹雪［47］。Ding等［48］在青藏高原地区通过研究不同的降水类型与温度之间的关系，使用一种新的指数曲线法对降水类型进行分割，他认为双温度阈值法对青藏高原地区降水类型的分割十分准确，但是该方法并没有在融雪径流模型中进行验证。

本文所使用的地面站点数据中只有1979年以前的数据标记了降水类型。本文基于拉萨河流域内外4个站点（拉萨站、当雄站、那曲站和嘉黎站），计算了1957—1979年拉萨河流域不同降水类型的比例。从图8中可以看出，不同的降水形态转化主要发生在1℃～9℃之间。当温度小于1℃时，降水的主要形态为降雪；随着温度的升高，降雪发生的频率逐渐减小，但降雪发生的频率要大于降雨的频率；当温度升高到2.93℃时，降雪的频率等于雨夹雪的频率，此时降水与降雪开始转换；当温度达到4.52℃时，降雨的频率等于雨夹雪的频率，此时雨夹雪的频率也在峰值附近，此后随着温度的升高降雪的频率逐渐降低，直至频率为0。

图8 不同降水类型在降水中频率随温度变化

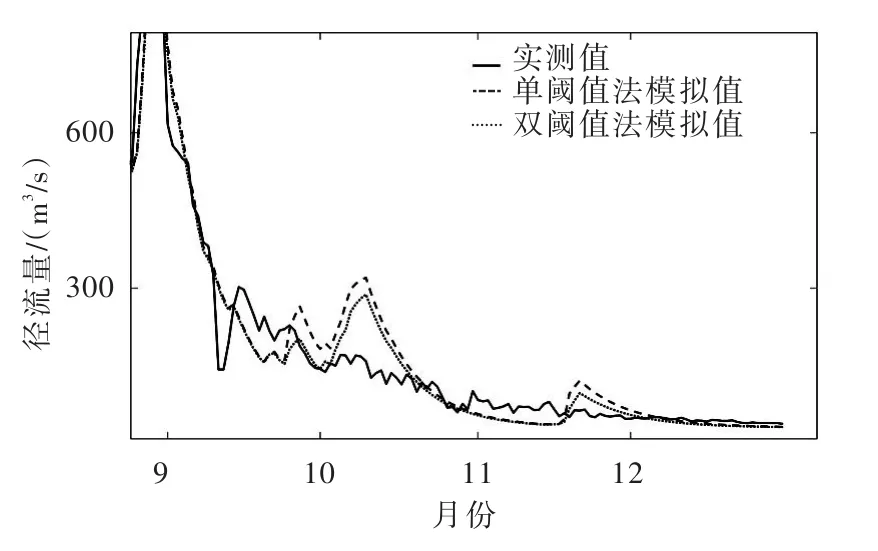
图9 使用单温度阈值法和双温度阈值法在拉萨河流域融雪径流模拟（2011年）

根据Liu和Ding等［47-48］的指数曲线法，本文计算了拉萨河流域降水类型分割的双温度阈值函数（式（12））。在拉萨河流域临界最低温度和临界最高温度分别为2.93℃和4.52℃，也即当温度小于2.93℃时，降水中100%的降水量均为降雪量；当温度高于4.52℃时，降水中100%的降水量均为降雨量；当温度介于两者之间时，降水事件中的降雪量所占的比例根据式（12）计算，而降雨量等于所占的比例等于1-降雪量比例。

式中：Sp为降水量中降雪量所占的比例；T为温度，℃。

以2011年站点为例，利用双温度阈值法对降水进行分离，分别计算降水量中降雨和降雪所占的比例，并将分离后的降水变量驱动融雪径流模型进行模拟。使用单阈值法分离降水类型的NSE数值为0.896，使用双温度阈值法分离降水类型的NSE数值为0.908。使用两种方法模拟结果的不同主要体现在9月中旬到12月初，特别是在10月份左右（图9），双温度阈值法在一定程度上降低了模拟的高估值。

5.2 季节尺度对模拟结果影响 时间尺度同样影响融雪径流的模拟精度，一般而言，模型在融雪季的模拟精度要高于非融雪季的精度。对融雪径流模型在春、夏、秋、冬尺度上分别进行模拟，使用单阈值法的NSE数值分别为-2.321、0.625、0.748和-0.817。从模拟结果中可以看出，融雪径流模型在夏季和秋季的模拟精度远高于春季和冬季的模拟精度，也就是融雪季的精度要远高于非融雪季的精度。利用双温度阈值法在四季尺度上模拟，则夏季和秋季的NSE数值分别为0.621与0.750，春季和冬季的NSE数值分别为-1.037和-0.782。从结果中可以看出，模型在9月中旬到2月初的精度得到一定程度的提高，双温度阈值法的融雪径流模拟主要提高了非融雪期的模拟精度。因此使用双温度阈值法对降水类型进行分割，可以在一定程度上提高融雪径流的模拟精度，这也是融雪径流模拟接下来进行改进的一个方向。

6 结论

本文基于改进的逐步订正法构建了降水输入模块，并与融雪径流模型SRM相耦合，以拉萨河作为研究区评估改进后的耦合模型在半干旱高寒地区对融雪径流的模拟效果。相比于传统的SRM模型，耦合降水输入模块的融雪模型能够有效提高融雪径流模拟效果。本文得出以下主要结论：（1）原始的TRMM降水卫星反演地面站点降水的相关系数、百分偏差分别为0.307和49.0%，精度相对较低。经过降水输入模块校正的降水卫星反演地面降水的精度得到显著的提高，其相关系数、百分偏差分别达到0.839和0.7%。（2）改进后的融雪模型的NSE和PBIAS在率定期分别为0.741和14.5%，比原始的SRM模型分别高出了0.046和减小了15.8%。NSE和PBIAS在验证期分别为0.770和15.4%，比原始的SRM模型分别高出了0.026和减小了7.4%。经过改进的融雪模型能够提高半干旱高寒区融雪径流模拟的精度。

本文利用基于地形因子改进的逐步订正法构建降水输入模块并将其与融雪模型进行耦合，在半干旱高寒区的拉萨河流域进行了试验，验证了模型的合理性和有效性，为缺资料地区的半干旱高寒区融雪径流模拟提供了一种有效的研究思路。