强降雨作用下山区岸滩稳定性演化分析

秦卫星，胡惠仁，周作霖，王江营



强降雨作用下山区岸滩稳定性演化分析

秦卫星1, 2，胡惠仁1, 2，周作霖1, 2，王江营1, 2

(1. 长沙理工大学 水利工程学院，湖南 长沙 410114；2. 水沙科学与水灾害防治湖南省重点试验室，湖南 长沙 410114)

根据Boussinesq非稳定渗流微分方程推导降雨和水位涨落联合作用下山区岸滩浸润线位置的解析解，基于Morgenstern-Price法获得考虑浸润线影响的岸滩抗滑稳定安全系数表达式。以某山区岸滩为研究对象，结合强降雨导致的水位涨落特点，根据建立的浸润线解析解和稳定性分析方法快速揭示强降雨过程及雨停后岸滩渗流与稳定性演化规律并分析原因。研究结果表明：降雨初期，河水位不变，雨水入渗导致浸润线逐渐抬升，向坡外的渗流力变大，岸滩安全系数逐渐减小至1.095，略小于允许安全系数；随着降雨持续，浸润线因雨水入渗和河水位快速上涨共同作用全面抬升，仍向坡外渗流，坡面水压力增加，岸滩安全系数呈增大趋势；降雨停止后，浸润线先因河水位持续上涨而抬升至最高位置，再随水位下降而降低，渗流方向先由朝坡外转向坡内再转向坡外，坡面水压力先增加后减小，岸滩安全系数先增加至最大值1.349后急剧减小至最小值1.062。建议重点加强降雨初期河水位上涨前和雨停后河水位下降时2个阶段的岸滩浸润线位置和稳定性监控，防止岸滩发生崩岸失稳。

山区岸滩；稳定性；浸润线；演化规律；强降雨

山区耕地稀少，河流沿岸的平坦冲积滩地常被开垦为农田，然而岸滩崩岸失稳常危及耕地安全，雨水入渗和水位涨落作用是岸滩破坏的主要诱 因[1−4]。山区河流洪水常因暴雨汇流而成，洪水过程历时短、水位涨落快，其涨落过程呈现出显著的阶段性特点。通常可用4个阶段描述强降雨导致的水位涨落过程：降雨初期−水位不变(阶段1)、降雨持续−水位上涨(阶段2)、降雨停止−水位持续上涨(阶段3)、水位回落(阶段4)。由此可见，河水位涨落的启动和结束时刻分别滞后降雨开始和停止时刻，强降雨作用下的岸滩渗流场在不同阶段分别受雨水入渗、水位涨落单独或联合影响。因此，准确判断强降雨作用下不同阶段的岸滩浸润线位置并揭示岸滩稳定性演化规律，及时给出安全预警与防护对策，对保证岸滩稳定具有重要现实意义。雨水入渗、水位涨落作用下的岸坡灾变机理一直是岸坡稳定性评价和防治研究的热点。王延贵[5]研究了洪水涨落过程的黏土岸滩稳定性，指出洪水迅速上涨时在水压力作用下岸坡稳定性增加，而洪水骤降时因向坡外渗流导致岸坡稳定性降低，河岸崩塌破坏风险增大。陆彦等[6]研究了水位涨落时岸坡渗流对边坡稳定性的影响，表明岸坡稳定的影响大小和坡中水体渗流方向密切相关，并得到了岸坡临界稳定坡度最小时的渗流方向计算公式。张华庆等[7]利用Abaqus分析了降雨入渗对软土岸坡稳定性的影响，指出持续强降雨易诱发岸坡失稳。宗全利等[8]计算了不同水位情况河岸稳定安全系数，研究表明退水期的稳定安全系数明显低于枯水期和高水期，涨水期稳定安全系数随水位升高呈先减小后增大趋势。张琳琳等[9]采用极限平衡法分析了汛后退水期库岸边坡稳定性变化规律，结果表明水位降落越快，河岸越不稳定。方景成等[10]利用敏感性系数法研究了库水涨落、降雨强度对岸坡稳定性的影响，指出水位下降和雨水入渗联合作用对岸坡稳定性减小影响最大。综上所述，目前的研究成果均表明雨水入渗和水位涨落是影响岸坡渗流场和稳定性的主要因素，但针对强降雨作用诱发水位涨落全过程山区河流岸滩渗流与稳定性演化规律的研究还少见报道，不利于正确评价岸滩稳定性和及时采取岸坡失稳防范措施。本文首先基于Boussinesq非稳定渗流微分方程，根据山区河流岸滩水文地质特征引入合理假定，推导了降雨与水位涨落联合作用下山区岸滩浸润线解析解。然后基于Morgenstern- Price法获得了考虑浸润线影响的岸滩抗滑稳定安全系数表达式。最后以某山区流域岸滩为研究对象，结合强降雨导致的水位涨落特点，利用浸润线解析解和抗滑稳定安全系数表达式快速揭示了强降雨作用下岸滩渗流与稳定的演化规律并分析了演化原因，明确了重点监控阶段和监控重点内容，为山区河流岸滩防灾减灾提供了技术支撑。

1 理论分析

1.1 浸润线求解

1) 基本假定

根据山区岸滩的水文地质特征，引入如下基本假定条件：①岸滩组份均质、侧向无限延伸，有近水平不透水层；②岸滩临河侧垂直、上表面近水平；③岸滩渗流为一维流；④河道水位等速涨落；⑤降雨按雨强值补给浸润线。岸滩浸润线计算简图见 图1。

图1 岸滩浸润线计算简图

根据上述假设条件，由Boussinesq非稳定渗流基本微分方程，可得：

式中：为渗透系数，m/d；为水头高度，m；为含水层厚度，m；为给水度或贮水率；为降雨强度，m/d；为水位涨落时间，d。

用始、末时段含水层平均厚度h代替式(1)中含水层厚度，则有：

2) 计算模型及边界条件

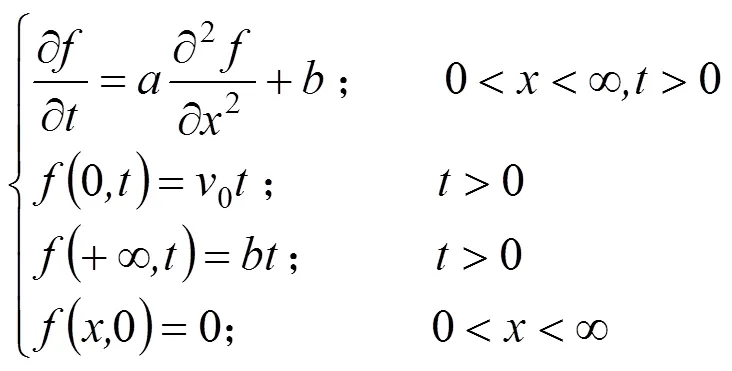
3) 浸润线位置

利用拉普拉斯正、逆变换对方程组(3)各式进行求解[11−15]，可得：

进而得到降雨与水位涨落联合作用下距临河侧处岸滩时刻浸润线计算的简化公式为：

采用式(6)对文献[12]所给算例进行计算，获得的浸润线结果与有限元数值模拟结果规律完全相同，误差在4%以内，证明推求的浸润线解析解可较好地满足实际岸滩浸润线位置预测需要，为快速预测强降雨作用下岸滩浸润线位置提供了一种简单便捷的分析手段。

1.2 岸滩抗滑稳定安全系数计算

刚体极限平衡法因抓住了边坡稳定性的主要矛盾、力学模型简单、使用方便等优点在边坡稳定性分析评价中得到广泛应用，主要有瑞典圆弧法、毕肖普法、剩余推力法和Morgenstern-Price法(简称M-P法)等[16]。前3种方法对土条间相互作用力进行了不同的简化处理，M-P法则适用任意形状的滑裂面，考虑了条块的静力平衡和力矩平衡，可更好地体现土条间的实际相互作用。因此，本文根据岸滩水文地质特征，基于M-P法推导了考虑浸润线影响的岸滩抗滑稳定安全系数计算公式。

取岸滩第条块作为研究对象，其高度为h，宽度为b，底面倾角为α，受力分析见图2。条块共受以下7组力：1) 条块自重W；2) 外力Q，其与竖直方向的夹角为β；3) 滑面所受的总水压力U，U=ubsecα，u为单位水压力；4) 滑动面上总的有效正应力N′；5) 滑面处于极限平衡状态下的抗剪力S，S=(N′tanφ′+c′bsecα)/F，其中φ′和c′分别为有效内摩擦角和黏聚力，s为安全系数； 6) 条块间法向力E和E1，与底面的距离分别为z和z−1；7) 条块左右侧剪切力λfE和λf−1E−1，其中λf和λf−1分别为条间法向力与剪切力的比值函数()在第条块左右侧的值，为比例系数，()为可采用半正弦函数计算的条间力函数。式(7)~(13)中的变量意义同上。

图2 第i条块受力分析图

由条块受力平衡可得沿滑面和与其垂直方向的平衡方程：

消除N′，则有：

进一步简化式(8)有：

式中：

根据岸滩首、尾条块静力边界条件有：0=0，E=0，再由式(9)可得岸滩抗滑稳定安全系数s为：

同理，对条块基底中心取矩得第个条块力矩平衡方程：

根据岸滩首、尾条块力矩边界条件有：0=0，M=0。由力矩平衡方程可以解出比例系数：

先根据式(6)推求浸润线位置，再通过对式(10)和式(13)进行迭代计算即可快速求得强降雨作用下岸滩抗滑稳定安全系数。

2 强降雨全过程岸滩稳定性分析

2.1 工程概况

湖南省某山区河流，流域面积391 km2，干流全长59 km，干流平均坡降4.15‰。河道弯曲，上游穿行高山峡谷之中，中下游形成较多平坦冲积滩地，岸滩土壤适合植物生长，大多被开垦为农田见图3。6~7月份经常遭遇短历时、高强度暴雨，雨水汇聚形成短时洪水，导致河道水位暴涨暴落，常诱发岸滩崩岸。

图3 山区典型岸滩

2.2 计算模型与计算条件

选取典型岸滩作为研究对象建立相应计算模型，计算简图见图1，模型长、高分别为30 m和25 m。岸滩水平隔水板高程为120.0 m，岸滩土体渗透系数为0.5 m/d，给水度为0.08，黏聚力′为39.4 kPa，内摩擦角′为17.4°。河床高程为128.0 m，初始水位为132.3 m，初始浸润线近水平。

近30 a降雨监测数据显示流域常遭遇15 h左右的持续强降雨，平均雨强为0.5 m/d。根据2015版《湖南省暴雨洪水查算手册》进行产汇流计算，得到该典型岸滩处强降雨引起水位涨落变化过程见图4，可分为4个阶段：1) 0~3 h内，水位基本不变，岸滩渗流稳定性主要受雨水入渗影响，为阶段1；2) 3~15 h内，降雨持续，河水位逐渐上涨至134.1 m，岸滩渗流稳定性受降雨和水位上涨联合影响，为阶段2；3) 15~17 h，降雨停止，由于雨水汇流的滞后性，水位持续上涨至最高136.4 m，岸滩渗流稳定性主要受水位上涨影响，为阶段3；4) 17~28 h，水位逐渐回落至132.3 m，岸滩渗流稳定性主要受水位下降影响，为阶段4。

图4 河道水位随时间变化曲线

2.3 岸滩渗流与稳定性分析

2.3.1 岸滩浸润线变化规律

根据强降雨作用下河水位涨落特点，采用式(6)可得强降雨作用下4阶段岸滩浸润线位置，见图5。

由图5可知：阶段1(0~3 h)降雨初期，河水位基本不变，岸滩内浸润线因雨水入渗逐渐抬升，渗流方向朝向坡外；阶段2(3~15 h)岸滩浸润线受水位上涨与雨水入渗共同作用全面抬升，但水位上涨速度较慢，坡内浸润线位置仍然高于临河侧浸润线，渗流方向朝坡外，表明该阶段雨水入渗比水位上涨对浸润线的影响大；阶段3(15~17 h)停雨初期，受水位持续上涨影响，逐渐高于岸滩内潜水面，导致渗流方向由朝坡外逐渐转向朝坡内；阶段4(17~28 h)雨停2 h后河水位开始下降并逐渐回归初始水位，而坡内潜水面下降较慢，导致渗流方向朝坡内变成朝坡外。

2.3.2 岸滩稳定性演化过程

根据SL386—2007《水利水电工程边坡设计规范》规定，该岸滩为5级边坡，采用M-P法计算岸滩稳定性时对应的允许安全系数为s=1.10。根据图5所示岸滩不同阶段的浸润线位置结果，采用式(10)和式(13)可快速求得岸滩相应阶段的稳定安全系数的变化曲线，见图6。

(a) 阶段1；(b) 阶段2；(c) 阶段3；(d) 阶段4

图6 安全系数演化图

1) 阶段1(0~3 h) 安全系数呈减小趋势，在阶段末达到1.095小于允许安全系数，岸滩处于危险状态。表明随雨水入渗，浸润线逐渐抬升，向坡外的渗流力变大，导致岸滩稳定性下降，失稳风险 增大。

2) 阶段2(3~15 h) 安全系数呈增加趋势。表明降雨持续，水位开始上涨，岸滩浸润线全面抬升，仍然往坡外渗流，作用在临水侧坡面的水压力变大，使岸滩稳定性逐渐增加。

3) 阶段3(15~17 h) 安全系数继续增加，达到最大值1.349。表明停雨初期，水位因汇流滞后性持续上涨，浸润线抬升至最高位置，作用在临水侧坡面的水压力进一步变大，使岸滩稳定性继续 增加。

4) 阶段4(17~28 h) 安全系数呈减小趋势达到最小值1.062，岸滩处于危险状态。表明雨停2 h后河水位下降并逐渐回归初始水位，作用在临水侧坡面的水压力急剧减小，岸滩内部水体无法及时排出使得朝坡外的渗透力急剧增加，导致岸滩稳定性下降，失稳风险增大。

综上所述，强降雨作用下岸滩渗流与稳定性受雨水入渗、水位涨落单独或联合影响，由于河道水位涨落的启动和结束时刻分别滞后于降雨开始和停止时刻，岸滩渗流与稳定性演变规律在降雨过程和雨停后整个过程表现出明显的阶段性特点，需要重点关注降雨初期水位未上涨和雨停后水位下降阶段的岸滩浸润线位置和岸滩稳定性。

3 结论

1) 降雨初期，河水位不变，雨水入渗导致浸润线逐渐抬升，向坡外的渗流力变大，岸滩稳定安全系数逐渐减小至1.095，略小于允许安全系数，岸滩失稳风险增加。

2) 随着降雨持续，浸润线因雨水入渗和快速上涨河水位共同作用全面抬升，仍然往坡外渗流，但坡面水压力增加，岸滩安全系数呈增大趋势。

3) 降雨停止后，浸润线先因河水位持续上涨而抬升至最高位置，再随水位下降而降低，渗流方向先由朝坡外转向坡内再转向坡外，坡面水压力先增加后减小，岸滩安全系数先增加至最大值1.349后急剧减小至最小值1.062，岸滩在雨停后水位下降阶段失稳风险增加。

4) 根据强降雨作用下岸滩稳定性演化规律，建议重点加强降雨初期河道水位上涨前和雨停后河道水位下降2个阶段的岸滩浸润线位置和稳定性监控，防止岸滩发生崩岸失稳。

[1] 李亮, 刘兴旺, 赵炼恒, 等. 降雨入渗对路基稳定性影响因素分析[J]. 铁道科学与工程学报, 2007, 4(2): 19− 23. LI Liang, LIU Xingwang, ZHAO Lianheng, et al. Factors analysis of subgrade stability due to rainfall infiltration [J]. Journal of Railway Science and Engineering, 2007, 4(2): 19−23.

[2] 刘兰芳, 邓美容, 廖梦思. 湖南省山洪灾害综合风险分析及安全减灾研究: 以2006年衡阳市山洪灾害为例[J]. 中国安全科学学报, 2009,19(10): 5−10, 179. LIU Lanfang, DENG Meirong, LIAO Mengsi. Comprehensive analysis of mountain torrent risk of Hunan province and its disaster reduction: a case study on the torrent disaster in Henyang city in 2006[J]. China Safety Science of Journal, 2009, 19(10): 5−10, 179.

[3] 赵炼恒, 罗强, 李亮, 等. 水位升降和流水淘蚀对临河路基边坡稳定性的影响[J]. 公路交通科技, 2010, 27(6): 1−8. ZHAO Lianheng, LUO Qiang, LI Liang, et al. Study on stability of subgrade slope along river subjected to water level fluctuation and stream erosion[J]. Journal of Highway and Transportation Research and Development, 2010, 27(6): 1−8.

[4] 赵志刚, 赵炼恒, 李亮, 等. 水位升降对顺层岩坡稳定性影响的上限分析方法[J]. 铁道科学与工程学报, 2012, 9(3): 51−57. ZHAO Zhigang, ZHAO Lianheng, LI Liang, et al. Upper bound stability analysis for parallel bedding rock slope subjected to water level fluctuations[J]. Journal of Railway Science and Engineering, 2012, 9(3): 51−57.

[5] 王延贵. 冲积河流岸滩崩塌机理的理论分析及试验研究[D]. 北京: 中国水利水电科学研究院, 2003. WANG Yangui. Study on mechanism of bank failure in the alluvial river[D]. Beijing: China Institute of Water Resources and Hydropower Research, 2003.

[6] 陆彦, 陆永军, 张幸农. 河道水位降落对边坡稳定的影响[J]. 水科学进展, 2008, 19(3): 389−393. LU Yan, LUYongjun, ZHANG Xingnong. Stability of river bank subject to drawdown of water level[J]. Advances in Water Science, 2008, 19(3): 389−393.

[7] 张华庆, 谭佳佳, 左殿军. 降雨入渗对软土岸坡稳定性影响研究[J]. 水运工程, 2014(4): 148−153, 167. ZHANG Huaqing, TAN Jiajia, ZUO Dianjun. Stability study of unsaturated soft soil slopes under rainfall infiltration[J]. Port & Waterway Engineering, 2014(4): 148−153, 167.

[8] 宗全利, 夏军强, 许全喜, 等. 上荆江河段河岸土体组成分析及岸坡稳定性计算[J]. 水力发电学报, 2014, 33(2): 168−178. ZONG Quanli, XIA Junqiang, XU Quanxi, et al. Soil composition analysis and slope stability calculation for riverbanks in the upper Jingjiang reach[J]. Journal of Hydroelectric Engineering, 2014, 33(2): 168−178.

[9] 张琳琳, 张耀哲, 张政. 落水条件下河道水库岸坡稳定性的分析研究[J]. 水力发电学报, 2015, 34(7): 12−20. ZHANG Linlin, ZHANG Yaozhe, ZHANG Zheng. Analysis of bank slope stability of channel reservoir during stage falling[J]. Journal of Hydroelectric Engineering, 2015, 34(7): 12−20.

[10] 方景成, 邓华锋, 肖瑶, 等. 库水和降雨联合作用下岸坡稳定影响因素敏感性分析[J]. 水利水电技术, 2017, 48(3): 146−152, 157. FANG Jingcheng, DENG Huafeng, XIAO Yao, et al. Sensitivity analysis on bank-slope stability impacting factors under joint-effect of reservoir water and rainfall [J]. Water Resources and Hydropower Engineering, 2017, 48(3): 146−152, 157.

[11] 郑颖人, 时卫民, 孔位学. 库水位下降时渗透力及地下水浸润线的计算[J]. 岩石力学与工程学报, 2004, 23(18): 3203−3210. ZHENG Yingren, SHI Weimin, KONG Weixue. Calculation of seepage forces and phreatic surface under drawdown conditions[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(18): 3203−3210.

[12] 冯文凯, 石豫川, 柴贺军, 等. 降雨及库水升降作用下地下水浸润线简化求解[J]. 成都理工大学学报(自然科学版), 2006, 33(1): 90−94. FENG Wenkai, SHI Yuchuan, CHAI Hejun, et al. The simplified solution of phreatic saturation line under the actions of rainfall and reservoir water level fluctuation[J]. Journal of Chengdu University of Technology (Science & Technology Edition), 2006, 33(1): 90−94.

[13] 张友谊, 胡卸文. 库水位等速上升作用下岸坡地下水浸润线的计算[J]. 水文地质工程地质, 2007(5): 46−49. ZHANG Youyi, HU Xiewen. Calculation of saturation line of groundwater under reservoir water table uniform rising[J]. Hydrogeology and Engineering Geology, 2007(5): 46−49.

[14] 吴琼, 唐辉明, 王亮清, 等. 库水位升降联合降雨作用下库岸边坡中的浸润线研究[J]. 岩土力学, 2009, 30(10): 3025−303. WU Qiong, TANG Huiming, WANG Liangqing, et al. Analytic solutions for phreatic line in reservoir slope with inclined impervious bed under rainfall and reservoir water level fluctuation[J]. Rock and Soil Mechanics, 2009, 30(10): 3025−3031.

[15] 陈艳萍, 明春英, 何庆辉. 复变函数与积分变换[M]. 北京: 科学出版社, 2015. CHEN Yanping, MING Chunying, HE Qinghui. Complex function and integral transform[M]. Beijing: Science Press, 2015.

[16] 袁聚云, 钱建固, 张宏鸣, 等. 土质学与土力学[M]. 北京: 人民交通出版社, 2009. YUAN Juyun, QIAN Jiangu, ZHANG Hongming, et al. Soil properties and soil mechanics[M]. Beijing: China Communications Press, 2009.

(编辑 涂鹏)

Analysis for stability evolution of mountain beach under heavy rainfall

QIN Weixing1, 2, HU Huiren1, 2, ZHOU Zuolin1, 2, WANG Jiangying1, 2

(1. School of Hydraulic Engineering, Changsha University of Science and Technology, Changsha 410114, China;2. Key Laboratory of Water-Sediment Sciences and Water Disaster Prevention of Hunan Province, Changsha 410114, China)

Firstly, analytical solution to the location of the phreatic line in the mountain beach under the combined action of rainfall and water level fluctuations was derived from the Boussinesq unsteady seepage differential equation. Then the expression of slope stability safety factor considering the influence of the phreatic line was obtained with the Morgenstern-Price method. Finally, the evolution law of the seepage and stability of a mountain beach during and after heavy rainfall was revealed based on the analytical solution to the location of the phreatic line and the expression of slope stability safety factor, in consideration of characteristics of the water level fluctuation caused by heavy rainfall. The results show that: At the beginning of rainfall, the phreatic line is mainly uplifted by infiltration of rainwater, the seepage force outside the slope becomes larger, and the stability safety factor gradually decreases to 1.095, which is slightly less than the allowable safety factor; With the continued rainfall, the phreatic line is raised by the joint action of rainwater infiltration and the rising water level, the water pressure on the slope increases, and the stability safety factor increases as well; Right after the rainfall, the phreatic line gradually rises to the highest position firstly due to the continuous rise of the water level, and then gradually decreases as the water level drops, the seepage direction firstly turns from outside the slope then to the inside of slope and finally to the outside slope, the surface water pressure increases firstly and then decreases, the stability safety factor firstly increases to a maximum value of 1.349 and then decreases sharply to a minimum value of 1.062. It is recommended that the monitoring of the phreatic line and stability of the mountain beach in the two stages before the rise of the river level and the beginning of the decline of the river level should be strengthened in order to prevent the collapse of the mountain beach.

mountain beach; stability; phreatic line; evolution law; heavy rainfall

10.19713/j.cnki.43−1423/u.2019.05.008

TU43

A

1672 − 7029(2019)05 − 1170 − 08

2018−06−26

国家自然科学基金资助项目(51208062)；湖南省交通科技计划资助项目(201140)

秦卫星(1978−)，男，湖北仙桃人，副教授，博士，从事岩土体结构变形与控制技术研究；E−mail：starqwx008@163.com