考虑挡墙变位模式的有限土体主动土压力试验研究

方焘，孙书翰，徐长节, 2，王海龙，杨锐锐，王宁



考虑挡墙变位模式的有限土体主动土压力试验研究

方焘1，孙书翰1，徐长节1, 2，王海龙3，杨锐锐3，王宁1

(1. 华东交通大学 江西省岩土工程基础设施安全与控制重点试验室，江西 南昌 330013；2. 浙江大学 滨海和城市岩土工程研究中心，浙江 杭州 310058；3. 南昌市政公用集团，江西 南昌 330000)

经典土压力理论中假定墙背后土体为半无限空间，墙后土体宽度减小至一定宽度时就不再适用。为研究有限宽度土体情况下的土压力分布特性，设计有限土体自动控制模型试验装置，采用福建标准砂，在测试砂土的物理力学特性和标定土压力量测元器件基础上，开展挡土墙绕墙趾及墙顶转动、平动等3种变位模式下的有限土体主动土压力分布特性模型试验研究；同时，运用极限平衡法计算得到各组试验主动土压力合力，与模型试验开展对比分析。试验结果表明：各填土宽度砂土主动土压力试验的破裂面均为直线，当宽度减小到一定值时，土体破裂棱体均由三角形变为梯形；随着填土宽度的减小，墙后土压力合力也随之减小；3种不同变位模式下土压力分布规律不同；极限平衡法计算结果与试验结果存在一定差异，最大相差6.1%。

有限土体；模型试验；主动土压力；变位模式；极限平衡法

随着城市化脚步不断加快，地下空间的利用率逐渐增加，拟开挖的深基坑与既有建筑物非常近接，如地铁附属结构围护结构与主体结构之间、主体结构与既有房屋建筑桩基础之间等，这些情况下支护结构与邻近既有建筑物之间就形成了有限宽度土体。目前，设计中对于有限土体土压力的计算多采用经典的朗肯土压力理论。而朗肯土压力理论假定墙后土体为半无限范围内的土体，所以，经典朗肯土压力理论已经不再适用于计算有限土体土压力。《建筑基坑支护技术规程》(JGJ120—2012)指出，在支护结构土压力的影响范围内，存在相邻建筑物地下墙体等稳定的刚性界面时，可采用库仑土压力理论计算界面内有限滑动楔体产生的主动土压力，此时，同一土层的土压力可采用沿深度线性分布形式，但没有给出具体破坏模式和土压力影响范围大小对土压力应力分布的影响。有很多学者采用理论、试验与数值分析方法考虑挡墙运动模式、刚度、变位等影响对土压力及有限土体土压力进行了深度研究， Frydman等[1]采用谷仓土压力公式计算临近基岩面挡土墙的无黏性土主动及静止土压力；高印立[2−3]利用土的塑性上限理论推导出无黏性土有限土体土压力的计算公式，对比分析了其与经典土压力理论的差异；马平等[4]基于极限平衡理论，在考虑土体黏聚力的情况下，认为滑裂面倾角是一个受多种因素影响的变值；Greco[5]针对挡墙与基岩间狭窄填土存在多条破裂面的情况，通过极限平衡法进行了有限土体土压力理论推导；林松[6]基于采用非线性Mohr -Coulomb 破坏准则，提出一个对刚性挡土墙的墙后被动土压力计算方法，分析和确定了滑动面的位置以及此时被动土压力的大小； Khosravi等[7]通过试验研究了平动模式下有限土体主动土压力变化，证明了土拱效应的存在；方焘等[8]分析了放坡条件下有限土体高宽比对土体剪切破坏角的影响；张亮等[9]借助极限分析方法上限定理，计算考虑孔隙水压力和通过拟静力法简化的水平和竖直向地震力作用下的二级边坡的挡土墙被动土压力的上限解；杨明辉等[10]以无黏性土为研究对象进行有限土体主动土压力模型试验，分析了其土体变形及土压力分布规律。王洪亮等[11]通过对挡土墙与既有建筑基础间的有限土体进行完整的受力分析，考虑了既有建筑基础与有限土体间的法向及切向相互作用力，建立了求解有限土体主动土压力的计算公式；张健等[12]在经典库伦主动土压力理论基础上，结合RB模式下土体渐进破坏机理，建立内摩擦角和墙背与土体之间摩擦角的发挥程度与土体发生位移的非线性关系，将其引入到土压力强度计算公式中，得到RB模式不同位移情况下的土压力强度公式。FANG等[13]展开了无黏性土刚性挡墙主动土压力试验研究，得出主动土压力强度分布规律，且其分布形式因挡墙变位模式的不同而变化。鉴于前人对有限土体主动土压力研究不系统、不全面，研究成果远不满足实践应用发展的需要，本文设计了自动控制挡墙3种变位模式的模型试验装置，以无黏性土为试验对象展开有限土体土压力试验，并且结合试验结果对滑裂面倾角及主动土压力合力进行系统理论分析，克服了过去试验手动控制挡墙位移带来的试验误差，进一步丰富了有限土体土压力理论，以期为实际工程提供更加合理的设计参考。

1 模型试验设计

1.1 模型试验装置

模型装置由①装土箱②填土宽度调节装置③刚性挡土墙④土压力埋设装置⑤挡墙变位自动控制装置⑥数据采集装置组成(见图1)。

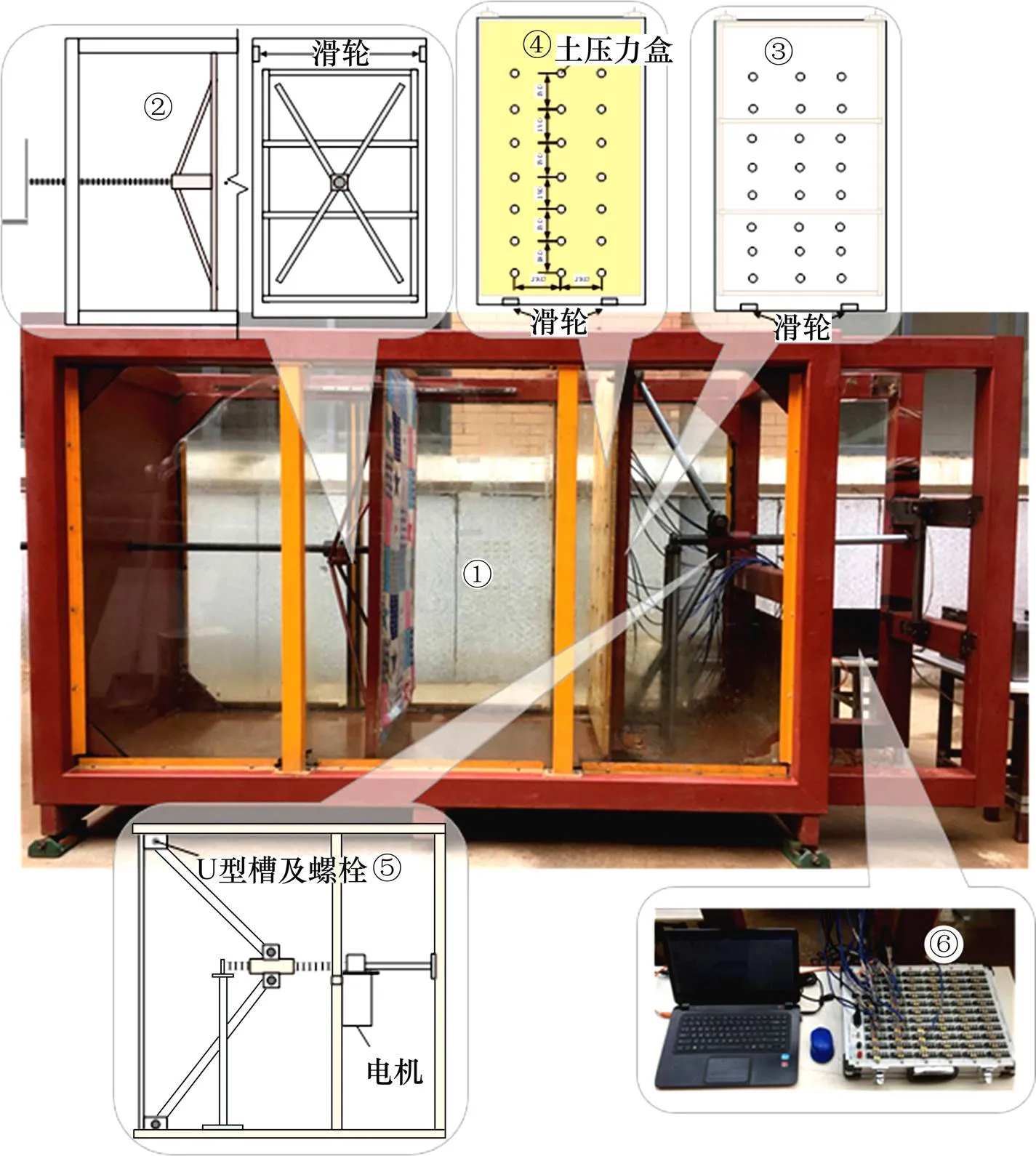
①—装土箱；②—填土宽度调节装置；③—刚性挡土墙；④—土压力埋设装置；⑤—挡墙变位自动控制装置；⑥—数据采集装置

①模型箱试验装置，尺寸为2 500 mm(长)× 1 000 mm(宽)×1 500 mm(高)，整体框架由100 mm宽方管焊接而成，试验装置底部焊接一块不锈钢钢板，左右两侧分别嵌固2块20 mm厚钢化玻璃，两侧玻璃之间的距离为800 mm。

②填土宽度调节装置，填土宽度调节装置由一块可移动透水挡板和一根带转盘的螺杆组成，可移动挡板高1 415 mm，宽796 mm。挡土板沿固定滑轨移动。

③刚性挡土墙，试验变位挡墙采用刚性挡墙。挡墙由一块钢板与一块实木木板固定贴合组成，其中木板一侧为迎土侧，钢板一侧与挡墙自动变位控制系统相连接。挡墙高1 400 mm，宽796 mm。挡墙在电机控制下可实现3种变位模式的运动。

④土压力盒埋设装置，变位挡墙与土体接触一侧设置了一块尺寸略小于钢板的木板，在木板中制作与土压力盒尺寸相同的凹槽将其埋设其中，土压力盒沿着木板中线及两侧对称且均匀布置3列，每列7个土压力盒。

⑤挡墙变位自动控制装置，变位挡墙右侧钢板的顶部与底部的中点处分别焊接2个U型槽，用钢管与螺杆上的运动装置相连接。通过拆卸钢管来实现不同的挡墙变位模式。螺杆末端与电机相连接，试验时，电机带动螺杆转动，螺杆上的套筒随螺杆上的螺纹前后运动，带动变位挡墙实现位移。

⑥数据采集装置本次试验的数据采集装置采用的是江苏东华测试技术股份有限公司DH3816N静态应变测试分析系统。土压力盒采用定制的电阻应变式土压力盒，规格为10~20 kPa。

1.2 土样物理力学参数

试验以福建标准砂作为试验土样。标准砂填筑前高温晾晒，含水量控制比较均匀，砂土样物理力学参数见表1。

表1 土体基本力学参数

1.3 实验方案设计

根据经典土压力理论，当挡墙高为1 300 mm且墙背倾角为0°时，通过理论计算，填土宽度需达到734 mm才能视为半无限土体，本次试验时绕墙顶、墙趾转动以及平动等3种变位模式共设置了5种填土宽度，分别为200，350，500，650和800 mm。总共模型试验组数为15组。

1.4 模型填筑

将晾晒干的土样从同一高度缓慢倒入填入装土箱中，并用自制的压实板压实，每次压实次数相同，基本控制压实能力，填土过程中每填一层便在土样边缘撒上一层薄薄的彩砂，这样分层填筑直至填土高度达到1 300 mm，之后静置土样2 h；为方便观察土体破坏模式，装填砂土时，在土体边缘分层装撒若干层红色彩砂。

2 试验结果分析

2.1 土体破坏模式

图2绕墙底转动模式下，破裂面均为直线，且不通过墙踵；破裂面均处于库伦破裂面的内侧，随着填土宽度的减小，破裂面逐渐向内侧收缩。当填土到达一定宽度(本次试验在650 mm至500 mm之间)时，土体破裂面由三角形变为了梯形，并且随着填土宽度的不断减小，梯形的短边也不断变大，且滑裂面倾角随着填土宽度的减小而不断增大。

图3绕墙顶转动模式下破裂面同样为直线，所有破裂面均通过墙踵，其滑裂面倾角略大于绕墙底转动模式，各破裂面均处在库伦土压力线的内侧，且随着填土宽度的减小逐渐向内收缩。

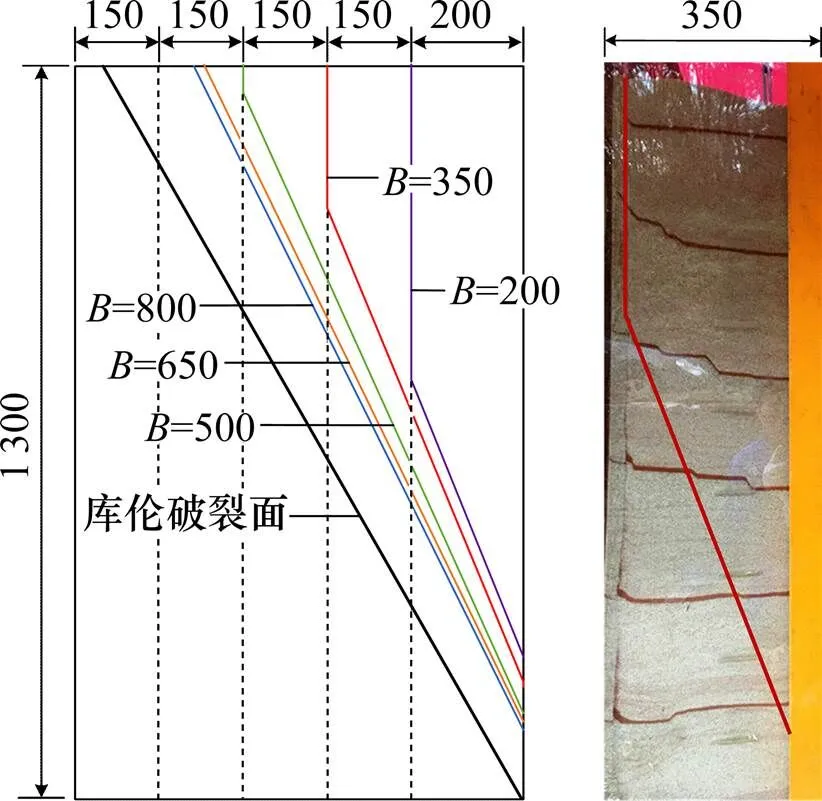
单位：mm

单位：mm

图4挡墙平动模式下各破裂面变形规律与绕墙顶模式下大致相同，其滑裂面倾角在3种变位模式中最小。

2.2 土压力分布规律

试验测得本次试验使用的土体内摩擦角= 31.1°，土体重度测定为=15.1g/cm3。

图5绕墙底转动模式下，挡墙上主动土压力呈线性分布，随着土体深度的增加逐渐增大，且均小于库伦土压力值。当填土宽度为半无限土体(即填土宽度为800 mm)时，其主动土压力线处于库伦土压力线内侧，较于库伦土压力减少了13%。随着填土宽度的减小，土体主动土压力值逐渐减小，主动土压力线也逐渐向内收缩，土压力值达到最小时，即填土宽度为200 mm时与库伦土压力相比减少了约42%。

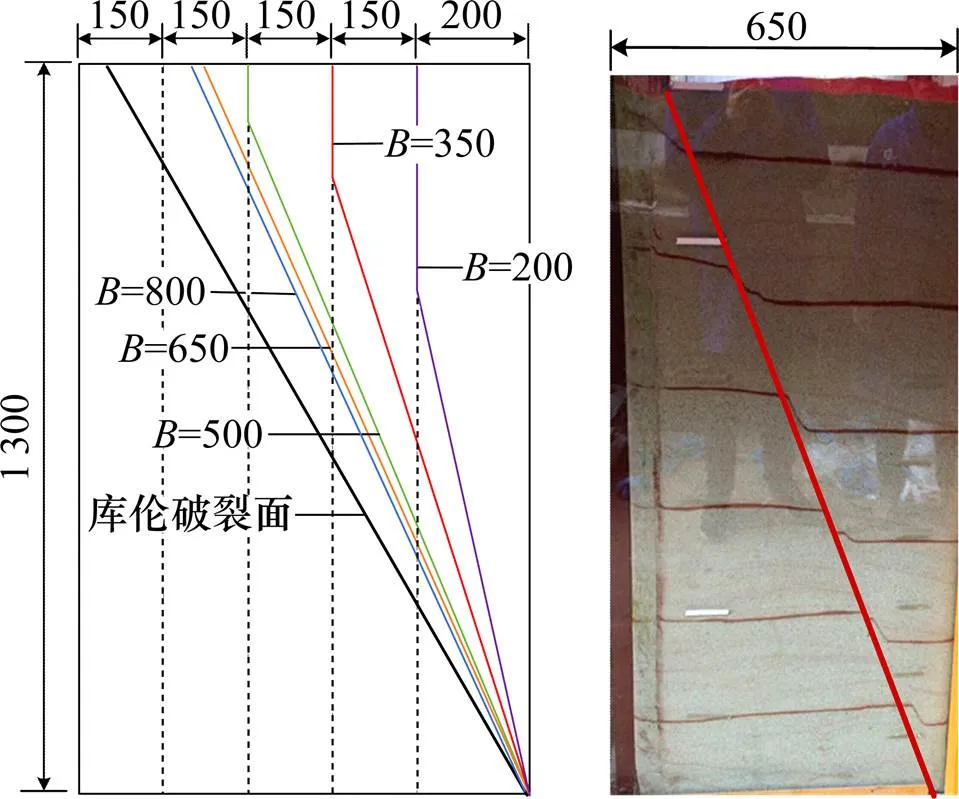
单位：mm

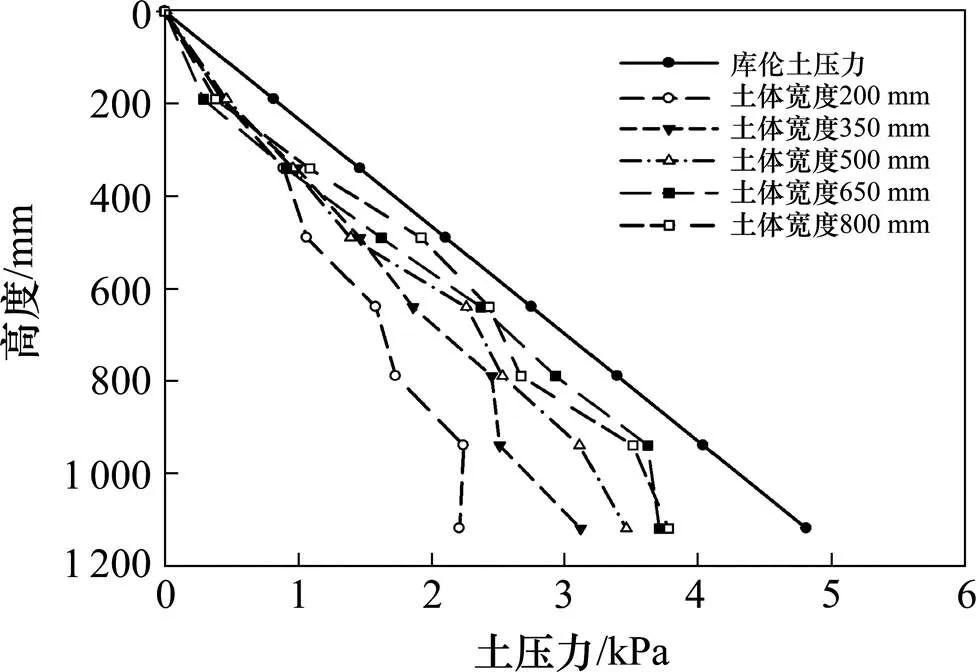
图5 绕墙底转动主动土压力

图6绕墙顶转动模式下，当填土宽度为500~ 800 mm时，上半部分主动土压力逐渐增大，这是由于填土宽度的增加而在墙后出现的土拱效应，这与前人[8]的试验结果一致。其土压力与库伦土压力相比最大增量达到113%。当填土宽度为200~350 mm时，主动土压力呈线性分布，主动土压力值随着土体深度的增加而增大。各填土宽度土体主动土压力值随着其宽度的减小逐渐减小，主动土压力线也随着填土宽度的减小逐渐向内收缩，当填土宽度为200 mm时达到最小，土压力值减少了43%。

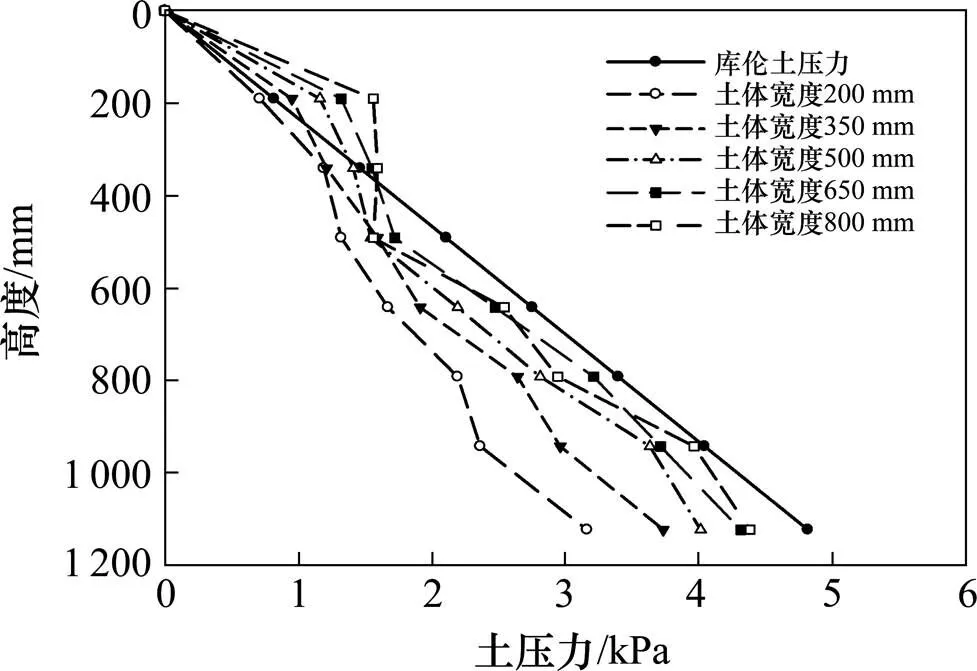
图6 绕墙顶转动主动土压力

图7挡墙平动模式下，下半部分主动土压力逐渐减小，其土压力值随着土体深度的增加先逐渐增大，在距离墙底约1/3土体高度处到达最大值，随后土压力值逐渐减小，并且明显小于库伦土压力值，土压力最大减少了41%。随着填土宽度的减小，土体主动土压力值也逐渐减小，其土压力线也随着填土宽度的减小逐渐向内收缩。

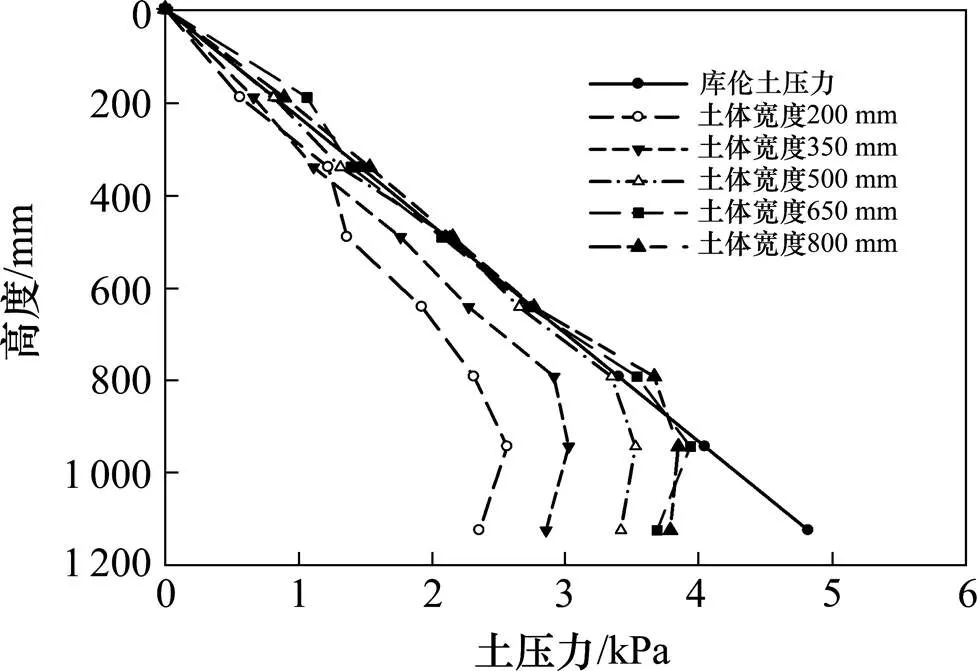
图7 挡墙平动主动土压力

各填土宽度在3种不同变位模式下的呈现出不同的土压力分布规律，为了对比不同变位模式下主动土压力之间的差异，将同一填土宽度下不同变位模式的主动土压力列出进行比较。

图8当土体宽度较为狭窄(本次试验填土宽度为200 mm)时，绕墙底转动模式下土压力明显小于其余2种变位模式，绕墙顶转动与挡墙平动模式下土压力差异不大，当填土宽度较大时，土体上半部分土压力值会明显大于其余变位模式。

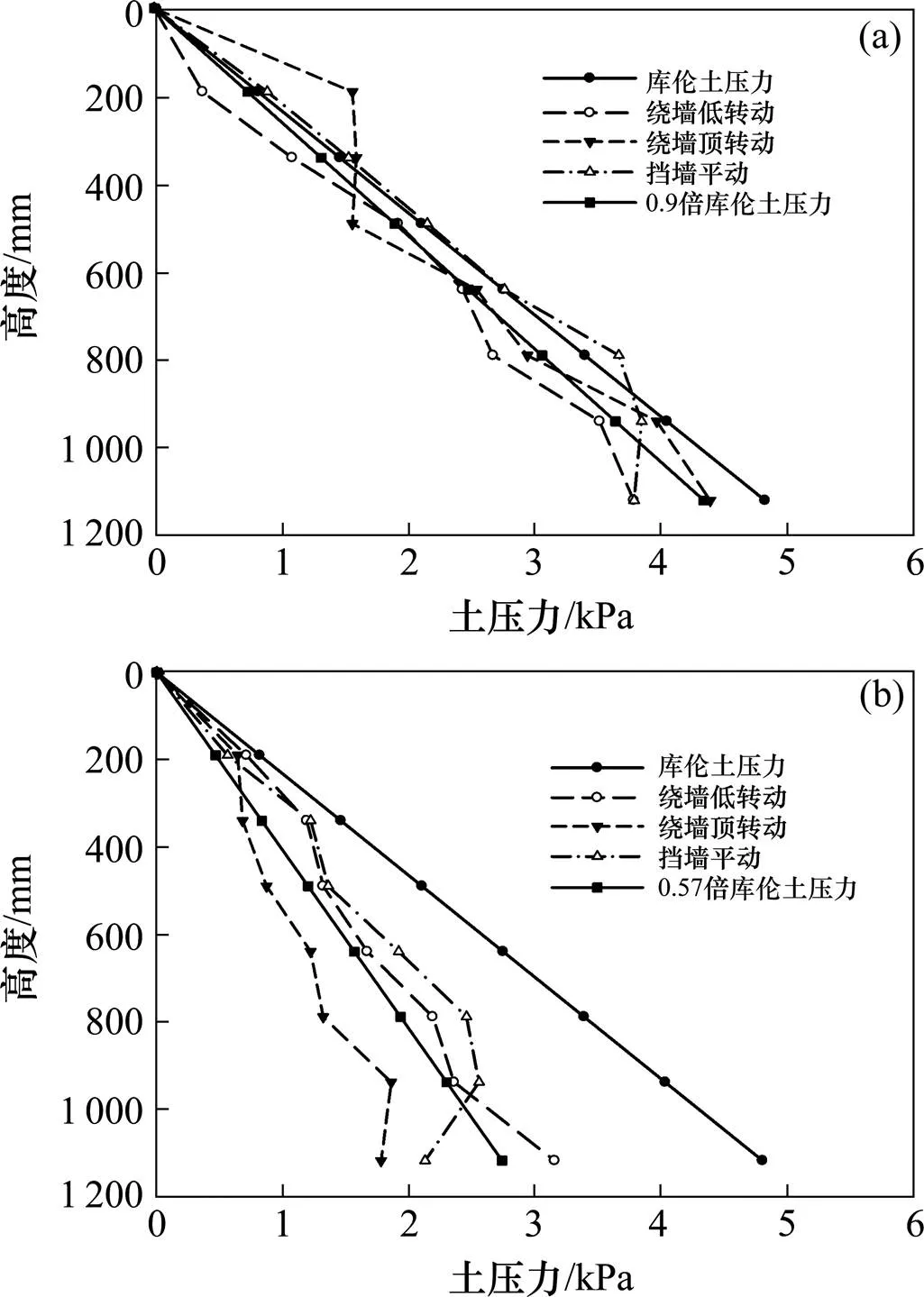
(a) 填土宽度为800 mm；(b) 填土宽度为200 mm

3 主动土压力合力分析

结合本次试验所得到的土体变形规律，基于极限平衡理论对建立砂性有限土体计算模型。为了便于分析，进行以下基本假定：

1) 土体为均质、各向同性的无黏性土，满足Mohr-Coulomb准则(2)土体破裂面为平面，破坏是一个平面应变问题。

当填土宽度不小于650 mm时，土体破坏形成的滑动楔体为一个三角形，见图9。

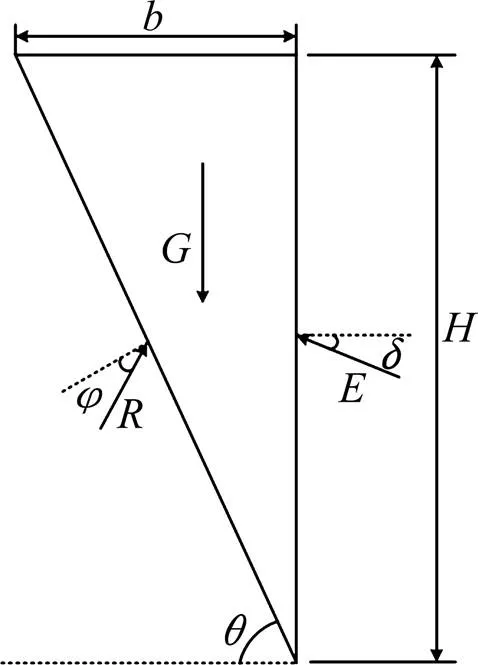
图9 三角形滑动楔体计算模型

由极限平衡法可以得到：

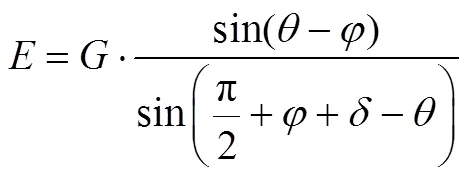
其中楔体自重为：

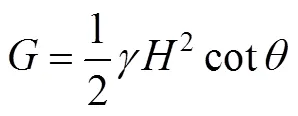
挡墙上反力的表达式为：

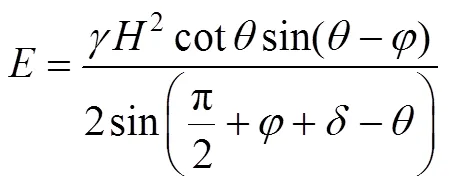
当填土宽度小于650 mm时，土体破坏形成的滑动楔体为一个梯形，见图10。

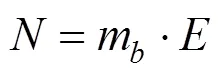
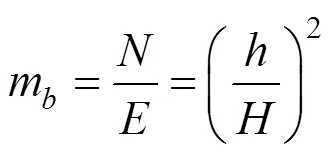
由土体受力平衡得到：

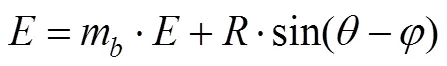
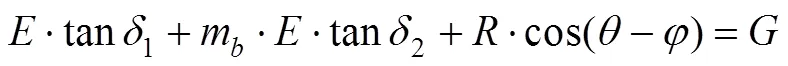
其中楔体自重为：

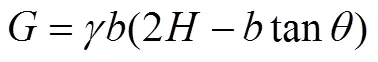
挡墙上反力的表达式为：

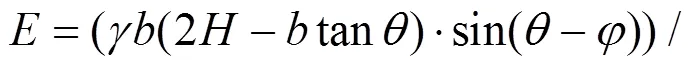
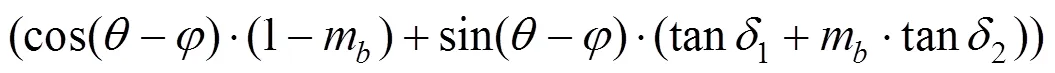
将各参数代入式(8)可以得到：

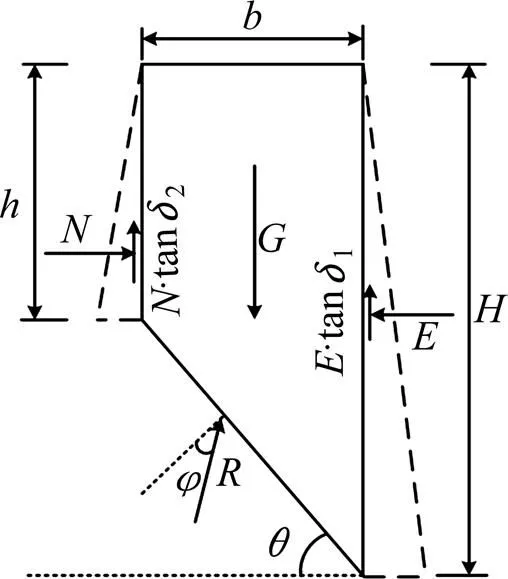
图10 梯形滑动楔体计算模型

图11绕墙底转动模式下，各填土宽度土体主动土压力理论计算值与试验所得结果差异不大，其差值最小为2.1%，最大为4.1%。随着填土宽度的增加，主动土压力逐渐增加；当填土宽度趋于半无限土体时，主动土压力增长放缓。分别对二者数据用二次多项式进行拟合分析，规律性非常明显。

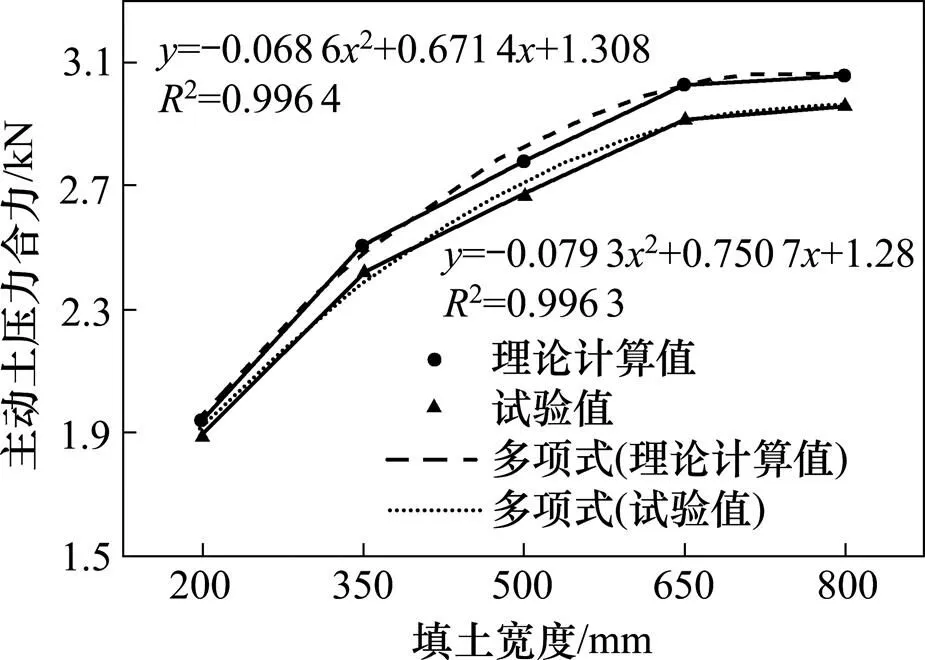
图11 绕墙底转动主动土压力合力

图12绕墙顶转动模式下，各填土宽度主动土压力理论计算值与试验所得结果同样存在一定差异，其差值最小为1.7%，最大为3.2%。其随宽度变化的土压力值变化规律与绕墙底转动下一致。同样得到拟合程度良好的2条趋势线。

图13挡墙平动模式下，计算与试验结果同样存在一定差异，其差值最小为3.8%，最大为6.1%。3种变位模式下，随宽度变化的土压力值变化规律基本一致。

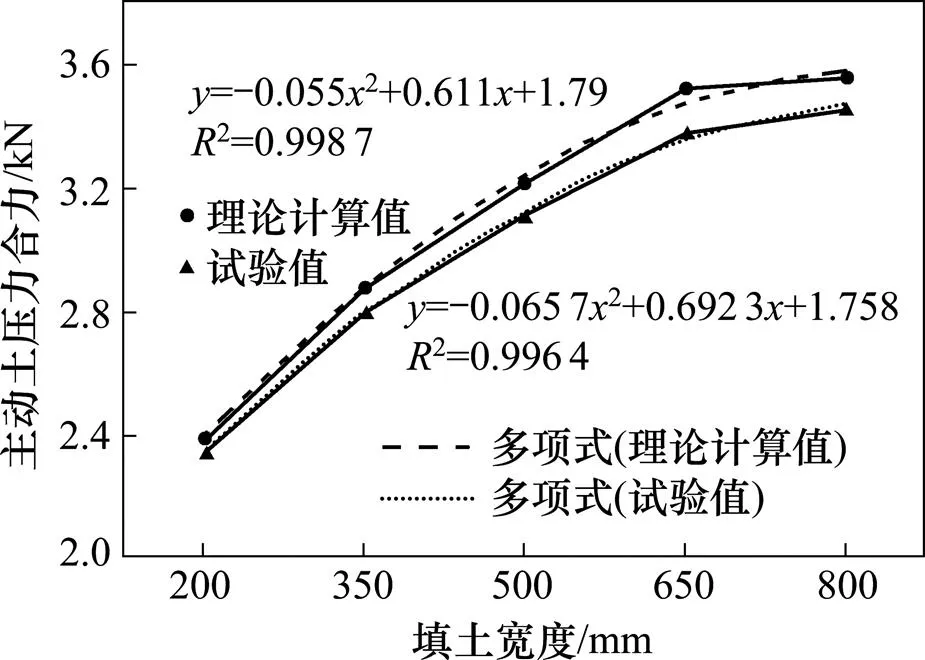
图12 绕墙顶转动主动土压力合力

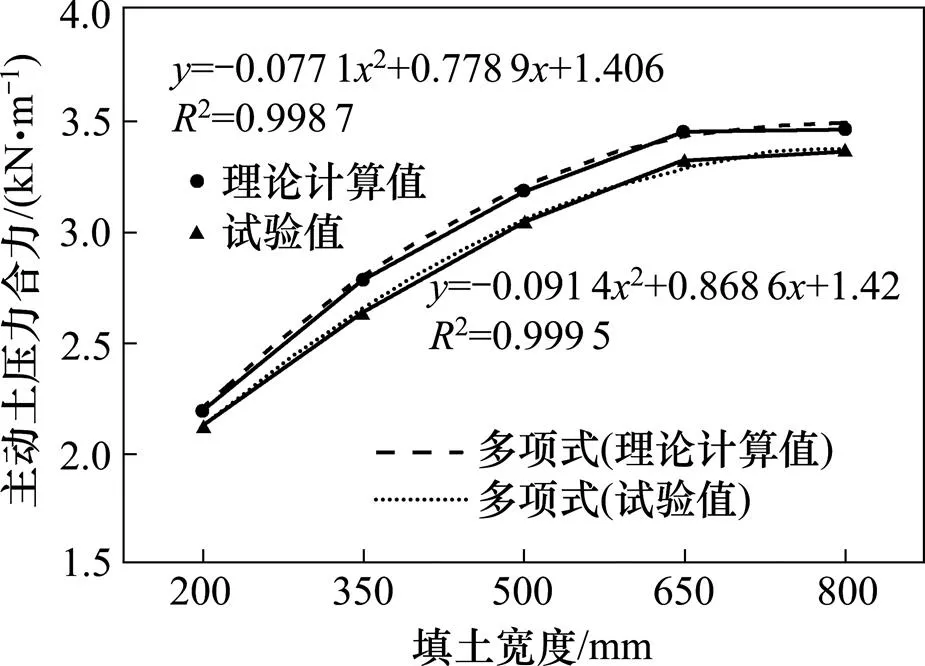
图13 挡墙平动主动土压力合力

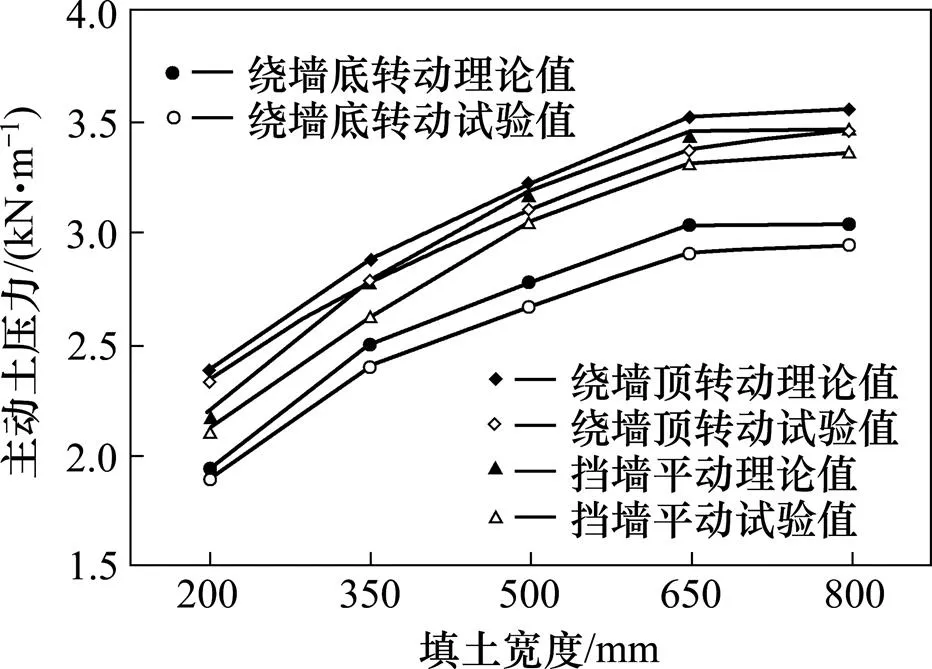
图14 主动土压力合力

图14土体主动土压力在3种变位模式下存在一定差异，其差值最大为23.2%。其中绕墙底转动模式下主动土压力明显小于其他2种变位模式。

4 结论

1) 各填土宽度砂土主动土压力试验的破裂面均为直线，且各破裂面均处在库伦土压力线的内侧。破裂面的剪切破坏角一直随着填土宽度的减小而不断增大，当宽度减小到一定值时土体破裂面由三角形变为了梯形。挡墙绕墙底转动模式下破裂面始终不会通过墙踵，挡墙平动及绕墙顶转动模式下破裂面均通过墙踵。

2) 有限土体主动土压力在3种变位模式下均小于库伦主动土压力值，并且随着填土宽度的减小其土压力值也逐渐减小。

3) 砂性有限土体主动土压力合力随着填土宽度的增加而增大，当填土宽度趋于半无限土体时，主动土压力增长放缓。结合试验结果，运用极限平衡法计算得到各组试验主动土压力合力，与试验结果差异不大，最大相差6.1%。

[1] Frydman S, Keissar I. Earth pressures on retaining walls near rock faces[J]. Journal of Geotechnical Engineering, ASCE, 1987, 113(6): 586−599.

[2] 高印立. 极限分析法计算有限范围土体土压力[J]. 建筑结构, 2001, 17(8): 66−68. GAO Yinli. Calculation of finite earth pressure by limit analysis[J]. Building Structures, 2001, 17(8): 66–68.

[3] 高印立. 有限土体土压力的计算探讨[J]. 建筑结构, 2000, 16(5): 53−56. GAO Yinli. The calculation of finite earth pressure[J]. Building Structures, 2000, 16(5): 53−56.

[4] 马平, 秦四清, 钱海涛. 有限土体主动土压力计算[J]. 岩石力学与工程学报, 2008, 27(增刊1): 3070−3074. MA Ping, QIN Siqing, QIAN Haitao. Calculation of active earth pressure for limited soils[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(Suppl 1): 3070−3074.

[5] Greco V. Active thrust on retaining walls of narrow backfill width[J]. Computers and Geotechnics, 2013, 50: 66−78.

[6] 林松. 非线性破坏准则下被动土压力的计算[J]. 铁道科学与工程学报, 2008, 5(4): 50−54. LIN Song. Calculation of passive earth pressure with nonlinear failure criterion[J]. Journal of Railway Science and Engineering, 2008, 5(4): 50−54.

[7] Khosravi M H, Pipatpongsa T, Takemura J. Experimental analysis of earth pressure against rigid retaining walls under translation mode[J]. Geotechnique, 2013, 63(12): 1020.

[8] 方焘, 王海龙, 杨锐锐, 等. 放坡条件下有限土体主动土压力计算[J]. 华东交通大学学报, 2016, 33(4): 50−55. FANG Tao, WANG Hailong, YANG Ruirui, et al. Active earth pressure calculation of limited soil in grading conditions[J]. Journal of East China Jiaotong University, 2016, 33(4): 50−55

[9] 张亮, 罗杰. 孔隙水作用下的二级边坡挡土墙被动土压力上限研究[J]. 铁道科学与工程学报, 2015, 12(2): 97–302.ZHANG Liang, LUO Jie. Upper bound analysis of passive earth pressure for reinforced slope under pore water pressure[J]. Journal of Railway Science and Engineering, 2015, 12(2): 297−302.

[10] 杨明辉, 戴夏斌, 赵明华, 等. 墙后有限宽度无黏性土主动土压力试验研究[J]. 岩土工程学报, 2016, 38(1): 131−137.YANG Minghui, DAI Xiabin, ZHAO Minghua, et al. Experimental study on active earth pressure of cohesi- onless soil with limited width behind retaining wall[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(1): 131−137.

[11] 王洪亮, 宋二祥, 宋福渊. 紧邻既有建筑基坑有限土体主动土压力计算方法[J]. 工程力学, 2014, 31(4): 76–81. WANG Hongliang, SONG Erxiang, SONG Fuyuan. Calclulation of active earth pressure for limited soil between existing building and excavation[J].Engineering Mechanics, 2014, 31(4): 76−81

[12] 张健, 王新征, 胡瑞林. RB模式下挡土墙主动土压力强度的计算研究[J]. 铁道科学与工程学报, 2016, 13(4): 675−681. ZHANG Jian, WANG Xinzheng, HU Ruilin. The study on active earth pressure against rigid retaining wall rotating about the base[J]. Journal of Railway Science and Engineering, 2016, 13(4): 675−681.

[13] FANG Y S, CHENG F P, CHEN R C, et al. Earth pressures under general wall movements[J]. Geotechnical Engineering, 1993, 24(2): 113−131.

(编辑 涂鹏)

Earth pressure experimental study of limited soil considering the mode of displacement of retaining wall

FANG Tao1, SUN Shuhan1, XU Changjie1, 2, WANG Hailong3, YANG Ruirui3, WANG Ning1

(1. Jiangxi Province Key Laboratory of Geotechnical Engineering Infrastructure Security and Control, East China Jiaotong University, Nanchang 330013, China; 2. Research Center of Coastal and Urban Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China;3. Nanchang Municipal Public Group, Nanchang 330000, China)

The classical earth pressure theory assumes the soil behind the wall is a semi-infinite space, however, it is no longer applicable when the width of the soil behind the wall decreases to a certain width. In order to study the earth pressure distribution characteristics in the case of soil with finite width, the automatic control model test device for finite soil was designed. The physical and mechanical properties of sandy soil were tested and the soil pressure force measuring elements were calibrated, then the three kinds of model tests, which were the rotation around the toe, the rotation around the top and translational motion of the wall, of limited active soil pressure distribution of the retaining wall were carried out by using Fujian standard sand. At the same time, the active earth pressure combined force of each group was calculated by the limit equilibrium method and the comparative analysis with model experiment were carried out. The test results show that the failure plane of the active soil pressure test of sandy soil with limited width is straight line. When the width decreases to a certain value, the soil failure surface changes from triangle to trapezoid, and as the width of the soil decreases, the resultant earth pressures behind the wall are also reduced, and the distribution law of earth pressure is different under three different displacement modes, in addition, the calculation results of limit equilibrium method are different from the test results, and the maximum difference is 6.1%.

limitedsoil; model experimental; active earth pressure; wall movement mode; limit equilibrium method

10.19713/j.cnki.43−1423/u.2019.05.009

TU411

A

1672 − 7029(2019)05 − 1178 − 08

2018−07−17

国家自然科学基金资助项目(51568021)

方焘(1976−)，男，安徽安庆人，副教授，博士，从事岩土工程、道路与铁道工程方面研究；E−mail：fangtaolq@163.com