变式才是硬道理
——一道二元最值问题的变式探究
陕西 李 歆
变式教学是数学教学过程中提高质量的重要手段,通过变式教学,有助于巩固学生的数学知识,培养学生分析、归纳、解决问题的能力,激发学生的学习兴趣,同时也是提高教师教学效率的重要保证.在教学实践中发现,对最基本的二元最值问题,学生往往感到比较棘手,处理时常常思路受阻,或者容易出错,其原因是对这类问题的变化规律没有掌握,导致变式的功能缺失,对此,本文对本刊责任编辑刘编辑在“数学变式兴趣研发群”中提出的一道二元最值问题的变式加以探究,供读者参考.
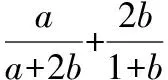
一、常规解法
由于问题式是由两个分子与分母都是一次的分式组成,所以容易想到用方程思想求解.
【解法1】先减元后用判别式
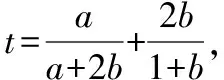

去分母后,整理得(3t-5)b2+(4t-2)b+t-1=0,


如果不用判别式法,那么用常用的解题工具——基本不等式行不行?
【解法2】先变形后用基本不等式
由已知条件及基本不等式,可得
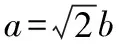
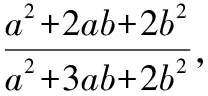
二、优美解法
【解法3】添项法一(先将1=2a+b代入第二项的分母)
由已知条件及基本不等式,可得
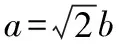
如果第二项的分母不变,而改变第一项的分母行不行?

由已知条件及基本不等式,可得
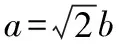
【点评】比较上述四种解法,前两种解法比较复杂,却是通解通法,属于基础层面,后两种解法十分简捷,但却需要抓住问题式的结构特征,对学生的观察能力有较高的要求,因此属于能力层面.在数学教学中,教师重视对通解通法的教学固然重要,但不能仅仅停留在基础层面,还要加强对学生解题能力的训练,所以在通解通法的基础上,倡导更加简便的优美解法,也是数学教学的主要任务.在下面的变式探究中,这种优美解法将会发挥举足轻重的作用.
三、变式与拓展
策略1:改变位置
1.分子与分母自身互换位置
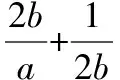
解:由已知条件及基本不等式,可得
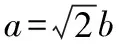
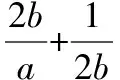
2.分子与分母交叉互换位置

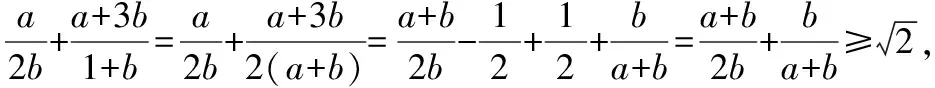


解:由已知条件及基本不等式,可得
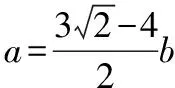
3.分子与分子,分母与分母互换位置
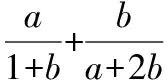
解:由已知条件及基本不等式,可得
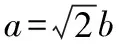
【点评】以上四种变式,变式1在互换位置后没有变化,是简单题,变式2、变式3和变式4在互换位置后,还对局部做了一些“微调”处理,属于基础题,四种解法都用到了“1”的代换技巧,变式2和变式3还用到了“添项法”,变式4还用到了“拆项法”,它们都是最基本的解题工具.
策略2:三角换元
由已知条件联想到三角公式sin2α+cos2α=1,可设2a=sin2x,b=cos2x,则有如下变式.

解:由已知条件及基本不等式,可得

策略3:等差换元
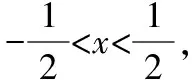
解:由已知条件可知, 5-6x>0,3-2x>0,又由基本不等式可得
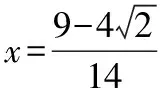
【点评】变式5和变式6都是将原来的二元最值问题转化为一元最值问题,如果按照习惯性思维,采用判别式法求解,则要复杂一些,但利用分子与分母的结构特征,用“添项法”处理却十分简捷.
策略4:升幂处理
1.将分子中的a变为a2,b变为b2,同时对第二项的分母做“微调”处理.
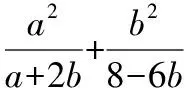
解:由已知条件及柯西不等式,可得
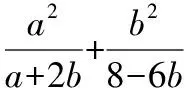
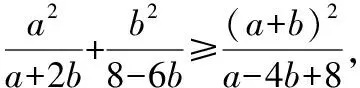

解:由已知条件及基本不等式,可得


策略5:改变常数项

解:由已知条件及基本不等式,可得
当且仅当4(m+b)2=2m(1+3b)2时等号成立,
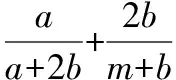
策略6:改变未知项
1.改变a的系数
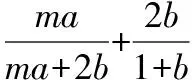
解:由已知条件及基本不等式,可得
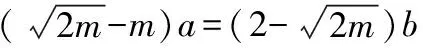
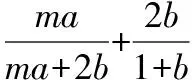
2.改变b的系数
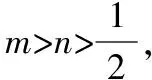
解:由已知条件及基本不等式,可得
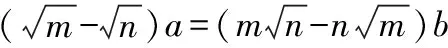

3.改变a和b的系数

解:由已知条件及基本不等式,可得
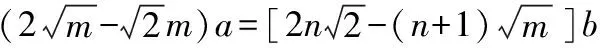
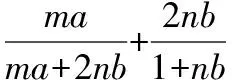
策略7:改变常数项和未知项

解:由已知条件及基本不等式,可得


【点评】与前面8个变式不同的是,后面的5个变式保留了上述问题的基本结构,只是从改变常数项及其变量的系数入手,将原有问题分别从几个不同的视角作了一般性地拓展,从而使原有问题的内在规律得以展示,在后面5个变式的解法中,都采用了“添项法”,但由于引入了常数参数,所以每一个变式添什么“项”,却不是一件容易的事,其中隐含了“待定系数法”的思想,值得读者去思考.


