小学数学练习设计的研究

李 烽

（江苏省海门市育才小学，江苏南通 226100）

引 言

课堂练习是数学教学中不可或缺的组成部分，是学生巩固知识、拓展思维、提升数学学习能力的重要手段。如何让小学数学练习的设计更有效，是教师一直在探索的问题。笔者结合多年教学经验，对小学数学练习设计做了如下研究。

一、巧用题型，夯实基础

每道数学练习题都是为了让学生更好地学习相关数学知识，因此，数学练习题的设计要立足基础、明确目标、突出重点。基础题涉及的知识点要单一，不可过于综合；题型要多样，如对比题、判断题是巩固基础知识常用的题型。

在教学苏教版四年级下册《解决问题的策略》这个单元时，有这样一道题目：小星和小泳共有78张卡片，如果小星给小泳8张，两人的卡片就会同样多，小星和小泳原来各有多少张卡片？在教学这道题时，可以出示下面这道题：小星和小泳共有78张卡片，小星比小泳多8张，小星和小泳原来各有多少张卡片？前一道题是移多补少的问题，第2题是和差问题，让学生比较两题有什么不一样，引导学生发现虽然两道题目中的总数都是78张，但是在前1道题移多补少问题中，小星给小泳8张以后，两人的卡片总数是不变的，还是78张，用78÷2=39（张），然后再倒推出小星原来有47张，小泳原来有31张。而在后一道题和差问题中，把小星多出的8张去掉，就转化成了小泳的2倍，此时两人一共有70张，总数发生了变化，用70÷2=35（张），算出小泳原来有卡片35张，再用35+8=43（张），算出小星原来有卡片43张。将两道题放在一起让学生辨析、思考，会给学生的认知带来比较强烈的冲击，能让学生深刻认识到移多补少问题与和差问题之间的异同点，使他们的认知结构更完整。

在数学概念的教学中，判断题是常用的题型，可以帮助学生深入认识数学概念的特点，规范数学语言，形成严密的数学思维。在教学新知之后，教师可以及时设计几道针对性强的判断题，让学生通过辨析，进一步理解新知、巩固认知、夯实基础。

二、变式拓展，发展思维

发展学生的思维能力是数学学习的重要目标。设计好每道练习题，挖掘每道题中的数学内涵，让学生每做一道题，都能经历一次思维锻炼的过程，丰富完善其各种思维方式，提升学生的数学素养。因此，我们对于现有的数学题，要进行适当的变式、有目的的拓展，为学生的思维发展服务[1]。

在学生了解了三角形的分类以后，会遇到这样一道题：一个等腰三角形的一个底角是70°，它的顶角是多少度？这是学生在学习了等腰三角形后的一道巩固练习题，属于基础题，涉及的知识点就是等腰三角形不仅两条腰相等，两个底角也相等，再联系三角形的内角和是180°，很容易就算出它的顶角是40°。我们可以将这道题进行适当的变式拓展，只要把“底”字去掉，就立刻提升了思维含量，将原题变为：一个等腰三角形的一个角是70°，它的另外两个角可能是多少度？变式后的题中没有明确这个70°的角是顶角还是底角，那么我们就需要分两种情况思考：假设70°的角是顶角，那么底角就是55°，所以另外两个角可能都是55°；假设70°的角是底角，那么顶角就是40°，所以另外两个角可能是70°和40°。这道题就会有两种不同的答案。将原题进行了一个小小的变化后，就运用到了假设的数学方法和分类思考的思维方式，有效拓展了学生的数学思维。

在《认识三角形》的教学中有这样一道题：在一个三角形中，如果有两个锐角的和小于90度，那么这个三角形一定是（ ）三角形。根据三角形的内角和是180度，很容易分析出第三个角一定大于90度，所以这是一个钝角三角形。在解答完这道题时，不能就此结束，教师应该趁机对原题进行变式：(1)如果在这个三角形中，有两个锐角的和等于90度，那么这个三角形是（ ）三角形。(2)如果在这个三角形中，有两个锐角的和大于90度，那么这个三角形是（ ）三角形。通过这样的变式题，让学生经过对比、辨析、总结的过程以后，学生对于三角形的内角和是180度这个知识点的认识，不会仅停留在知识点的记忆上，而是进入更深层次的理解，并且潜移默化地渗透了举一反三的学习方法和思维方式。

由此可见，教师需要用更高的视角，审视每道练习题，思考可以作出哪些变式和拓展，这样对学生掌握知识，拓展思维会有更大的帮助，甚至更有益于学生后续的数学学习。

三、重视方法，提升能力

数学学习不能仅满足于知识的获取这一层面，而应把提升数学能力作为更长远的目标。任何知识的学习都是为了解决实际问题，而解决实际问题则需要有更强的综合能力。因此，在设计数学练习时，不仅要围绕某些知识点设计习题，有时也需要淡化知识点，突出数学方法，围绕着数学思想、方法设计习题，如假设法、列举法、替换法、数形结合等数学方法，以此锻炼学生的数学综合能力，提升学生解决实际问题的能力。

例如，在苏教版四年级下册的教学中，有这样一道习题，如图1，左右两边处于平衡状态，一个圆柱体的质量是5千克，一个正方体的质量是4千克，那么请问一个长方体的质量是（ ）千克。虽然在这册教材中没有该题涉及的知识点，但是这道题包含了学生常用的等量转换的数学思想方法。可以先求出4个圆柱体和1个正方体的总质量是24千克，再根据图1中的等量信息，把它转换成3个长方体的总质量也是24千克，进一步再求出1个长方体的质量是8千克。其实，这道题除了应用等量转换的数学方法外，还渗透了五年级即将要学习的方程，为后续的数学学习打下基础。

图1

又如，王大叔要在同样大小的5块地里种柏树和松树，每块地里种5行树，每行种7棵，要求最外圈统一种柏树，其余种松树。王大叔要准备柏树苗和松树苗各多少棵？很多学生在读完题目后束手无策，按照以往解决实际问题时的经验，找不到互相有联系的条件，摸不着方向，有种有力无处使的感觉。但是如果像图2所示一样，画出其中一块地的示意图，就非常清晰了。○表示柏树，△表示松树，从图2中可以直接看出每块地里种了20棵柏树、15棵松树。那么5块地就需要准备100棵柏树苗、75棵松树苗。对于四年级的学生来说，这道题没有涉及任何有难度的知识点，重点考查的就是数形结合的思维方法。这就是我们常说的数学能力。我们不仅要围绕数学知识来设计习题，也要围绕数学方法来设计习题，只有这样，学生的数学能力才会得到锻炼和提升。

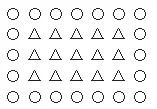
图2

结 语

总之，在练习设计时，题型的选择、题目的变式拓展以及对数学思想方法的重视等都决定了这份练习的质量，决定了学生学习数学的目标达成情况。一节好的数学课需要一份好的数学练习来辅助，通过有效设计数学练习，使学生在练习中夯实基础、发展思维，提高分析、解决问题的能力。