有轨电车特小半径曲线受力和变形特性
吴青松,段晓晖
(1.中交城市轨道交通设计研究院有限公司,湖北 武汉 430056;2.中交第二公路勘察设计研究院有限公司,湖北 武汉 430056;3.中铁第四勘察设计院集团有限公司 线站处,湖北 武汉 430063)
现代有轨电车线路投资少,建设周期短,具有节能环保、安全舒适、运能灵活等特点。现代有轨电车车辆采用独立轮对,左右2车轮解耦,独立转动[1],在曲线轨距不加宽条件下,能通过的最小曲线半径为15~30 m[2-4]。由于城市地形及道路条件限制,部分线路通过路口时采用特小半径曲线,通常半径为50 m。沈阳市浑南新区现代有轨电车采用一次建成槽形轨无缝线路,铺设半径为25~50 m的特小半径曲线共计20余处;武汉市大汉阳地区现代有轨电车无缝线路曲线最小铺设半径为50 m。
关于无缝线路铺设,TB 10015—2012《铁路无缝线路设计规范》[5]允许铺设无缝线路的最小曲线半径为300 m;GB 50157—2013《地铁设计规范》[6]中规定地下线曲线半径不小于300 m地段、高架线及地面线无砟道床曲线半径不小于400 m地段宜按无缝线路设计,允许最小曲线半径均未突破300 m。现代有轨电车允许最小曲线半径为35 m,困难条件下可至25 m[7],最小曲线半径为25~35 m已远远突破前述2个规范的限值。因此,有必要对有轨电车特小半径曲线段受力和变形特性进行研究。
研究有砟轨道无缝线路稳定性时采用统一的无缝线路稳定性计算公式[5],该公式有特定的使用条件,不适于有轨电车特小半径曲线段的研究。有轨电车整体道床结构刚度大,横向抗弯刚度为竖向的b/h2倍(其中b为宽度,h为高度);且由于上覆层的存在,道床结构温度变化较小,横向失稳可能性很小。为了综合考虑无缝线路下部整体道床对无缝线路受力和变形的影响,本文借助有限元软件进行研究。
1 计算模型
1.1 钢轨-道床三维空间耦合力学模型
以某有轨电车线路为例,特小半径曲线段为硬化铺装整体道床。受限于城市道路条件,通常不设置超高。轨道结构从上到下依次为60R2槽形钢轨、无枕式扣件、道床板、支承层和路基,扣件直接锚固于道床板,道床板与支承层通过层间黏接形成整体。曲线段线路受气温变化影响,钢轨、道床内部蓄积较大的温度力。随着温度力的增大,钢轨、道床发生变形,释放部分温度力,表现为径向分力,通过扣件传递至下部道床结构。此外,列车在通过曲线时,轮缘贴靠钢轨产生横向荷载,制动产生制动荷载,均通过扣件传递至下部道床结构。本文根据轨道结构纵横向受力特点,利用有限元软件建立钢轨-道床三维空间耦合力学模型,如图1 所示。

图1 钢轨-道床三维空间耦合力学模型
模型由直线段-曲线段-直线段组成,直线段和曲线段直接相连,未考虑缓和曲线连接。其中钢轨采用三维梁单元模拟,道床板、支承层采用实体单元模拟,扣件分别采用纵、横、垂3个方向的弹簧单元模拟。道床板与支承层间采用黏接模拟,支承层与路基间相互作用采用弹性地基模拟。考虑到扣件对钢轨的限位作用随线路方向的变化而变化,在直线段采用直角坐标系,x,y,z分别为线路纵、横和垂向;在曲线段采用柱坐标系,r,T,z分别为线路横、纵和垂向。
模型假定:①本文仅从轨道结构自身受力变形的角度出发,不考虑埋入式轨道硬化铺装及柔性材料;②假定直线段长度(100 m)足够消除边界条件影响,钢轨两端采用固定约束;③不考虑钢轨初始弯曲及运营维护线形偏差。
1.2 主要计算参数
参照统一公式,无缝线路临界容许温度力与曲线长度L、曲线半径R有关。为研究曲线长度、曲线半径对无缝线路受力和变形的影响,模型选取不同的曲线半径及曲线长度,最小圆曲线长度取15 m[7],最大圆曲线长度以对应圆心角不超过180°进行选取,共计34种曲线半径和曲线长度组合,具体见表1。

表1 不同曲线半径R和曲线长度L所对应的圆心角 (°)
60R2槽形轨弹性模量为206 GPa,泊松比为0.3,热膨胀系数为 0.000 011 8 /℃,横截面积为76.11 cm2,横向惯性矩为920.1 cm4;扣件垂向、横向弹簧为线性弹簧单元,刚度取50 kN/m[8];扣件纵向弹簧为非线性弹簧单元,极限位移2 mm,单组扣件阻力为9 kN,即单位长度扣件纵向阻力为14.4 kN/(m·轨)。道床板为C40混凝土,弹性模量为32.5 GPa,泊松比为0.2,热膨胀系数为0.000 01/℃。支承层为C25混凝土,弹性模量为28 GPa,泊松比为0.2,热膨胀系数为0.000 01/℃。
列车荷载:根据有轨电车列车荷载图式[9],列车横向荷载取为静轮载的0.8倍,即50 kN,单轮加载;加载位置分别为直圆点、圆曲线中点。
道床温度取值:有轨电车轨道结构为埋入式,交叉路口硬化铺装覆盖道床结构,道床结构上下温差变化较小,因此不考虑道床结构温度梯度。为考虑最不利影响,道床结构温度变化范围取气温变化范围。以武汉地区为例,历年最高气温39.6 ℃,最低气温-18.1 ℃,考虑混凝土施工温度为10~20 ℃,道床结构最大降温29.6 ℃,最大升温38.1 ℃。考虑混凝土收缩影响,分段灌筑的道床结构取等效降温10 ℃[10]。综上,道床温度取值最大降温、最大升温均取40 ℃。温度力与列车荷载组合时,采用最大日温差,日温差(升温或降温)取为20 ℃。
钢轨温度取值:武汉地区历年最高气温39.6 ℃、最低气温-18.1 ℃,取最高轨温59.6 ℃、最低轨温-18.1 ℃,设计轨温为20±5 ℃,钢轨最大升温44.6 ℃、最大降温43.1 ℃,均取为50 ℃。
1.3 荷载工况
特小半径曲线段轨道结构随着季节更替,钢轨温度偏离锁定轨温,道床温度偏离施工温度,在内部蓄积了较大的温度力。升温时,钢轨、道床向外膨胀变形;降温时,钢轨、道床向内收缩变形,变形过程中均伴随着温度力的释放。由于曲线段轨道结构存在初始弯曲,在温度升高情况下容易失稳破坏。因此,本文仅分析温度升高荷载工况。结合轨道结构实际运营情况,分析工况包含最大温度荷载和常用荷载组合,共计11组荷载工况(横向荷载作用位置包括直圆点和圆曲线中点),具体见表2。综合34种曲线半径及曲线长度组合和11组荷载工况,共计374个计算工况。

表2 荷载工况
2 计算结果分析
2.1 最大温度荷载对轨道受力和变形的影响规律
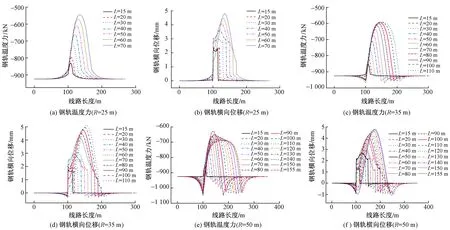
图2 最大温度荷载作用下钢轨受力和变形
最大温度荷载(工况1)作用下,钢轨温度力、横向位移计算结果见图2。可知,两端直线段钢轨温度力趋于水平,钢轨温度力与无缝线路固定区温度力一致,说明模型中钢轨边界条件假定合理。曲线两端直线段可视为无缝线路固定区,钢轨温度力无释放。直线段与曲线段之间为过渡段,此处钢轨温度力逐步被释放,随着曲线半径的增加,该段出现向内位移(负位移),半径越大、长度越长,受到直线段固定区的挤压越明显,在直圆点处达到最大,主要原因是曲率变化不连续。曲线段为钢轨温度力释放区,在连续支承层向外膨胀变形带动下,钢轨向外移动,整个钢轨温度力以曲线中点为中心呈对称布置,在曲线中点处达到最大值,对应的横向位移也达到最大值,钢轨温度力释放量与钢轨横向变形呈对应趋势。
综合受力和变形情况可知,曲线中点处钢轨温度力释放量最大,相对于直线段固定区,曲线半径为25 m 时,温度力释放量随曲线长度的增长而快速增大,其差值由94.3 kN增大至379.8 kN,最大横向位移则由2.34 mm增至4.78 mm;曲线半径为35 m时,温度力释放量随曲线长度的增长先快后慢地增大,其差值由74.2 kN增大至333.3 kN,最大横向位移则由1.78 mm 逐步增至5.13 mm,最大横向负位移约为0.3 mm;曲线半径为50 m时,温度力释放量随曲线长度的增长先增后降,其差值由62.8 kN先增至298.2 kN,再缓慢降至236.8 kN,最大横向位移则由1.35 mm逐步增至4.80 mm,最大横向负位移由0.04 mm 增至1.09 mm。上述位移均为钢轨绝对位移,包括钢轨和道床的整体横向变形,主要是道床向外膨胀变形带动发生的,而钢轨和道床间相对位移较小。相比于有砟轨道无缝线路横向失稳限值2 mm,上述计算结果已远超该限值,但由于无砟轨道刚度大,并未发生失稳破坏,轨道结构在最大温度荷载作用下发生横向向外4~5 mm的径向位移时,位移量在合理范围内,且此时轨道结构均处于线弹性阶段。计算结果表明,有砟轨道无缝线路横向失稳限值2 mm并不能很好地评价有轨电车特小半径曲线无缝线路受力状态。由于特小半径曲线段轨道结构整体横向位移较大,在钢轨与硬化铺装衔接处应采用可变形材料,以适应变形,防止挤压破坏。

图3 最大温度荷载作用下钢轨温度力释放量
图3为最大温度荷载作用下,考虑直圆点受压后的钢轨温度力的释放量。由图3(a)可知,曲线半径为25 m时,钢轨温度力释放量随曲线长度的增长而快速增大,由94.3 kN增大至379.8 kN;曲线半径为35 m 时,温度力释放量随曲线长度的增长先快速增大,曲线长度达到60 m后,温度力释放量增大速度降低,曲线长度为90~110 m时,温度力释放量几乎不再增长,最大释放量为364.8 kN;曲线半径为50 m时,温度力释放量随曲线长度的增长先快速增大,曲线长度达到80 m 后,温度力释放量增大速度降低,并出现释放量减小的现象,曲线长度为80 m时,钢轨温度力最大释放量为423.4 kN。由图3(b)可知,以圆心角90°为分界线,圆心角小于90°时,温度力释放量增长速度较快,大于90°后则增速减慢;圆心角小于150°时,曲线半径越小,温度力释放量越小,这主要是由于曲线半径大则所对应的线路长,其下部支承层为连续结构,在温度力作用下向外膨胀变形,会带动无缝线路横向位移和加大无缝线路温度力的释放。
结合实际选线工作,在线路经过路口时,通常线路中线是确定的,即线路偏转角(圆心角)确定,此时,可选用较小曲线半径通过路口。但曲线半径太小会限制有轨电车允许通过速度,延长通过路口时间,对交通影响较大,应综合考虑。
2.2 常用荷载对轨道受力和变形的影响规律
由前述分析可知,无缝线路在直圆点受到直线段固定区的挤压,承受较大的温度力;而圆曲线中点处横向位移、温度力释放量均达到最大。上述2处是无缝线路薄弱点,因此本文在常用温度荷载基础上,在上述2点分别施加横向荷载,以研究常用荷载对轨道受力和变形的影响规律。
轨道结构在常用温度荷载作用下,钢轨变形规律与前述最大温度荷载作用类似,在曲线段释放温度力。由于列车横向荷载的作用,在作用点两侧形成受力突变,左侧钢轨受力得到一定的释放,而右侧因受到无释放段挤压,反而有所增长。由于轨道结构整体刚度大,列车横向荷载仅对作用点附近受力有影响,而对整体几乎无影响。对计算结果分析可知,相同曲线半径和曲线长度下,对钢轨施加不同温度荷载,对钢轨受力突变两侧的差值几乎没有影响,即在同一点施加荷载工况2—工况6,计算结果基本相同。此外,计算结果表明,列车横向荷载分别在直圆点与曲中点时,钢轨受力突变两侧的差值基本一致。
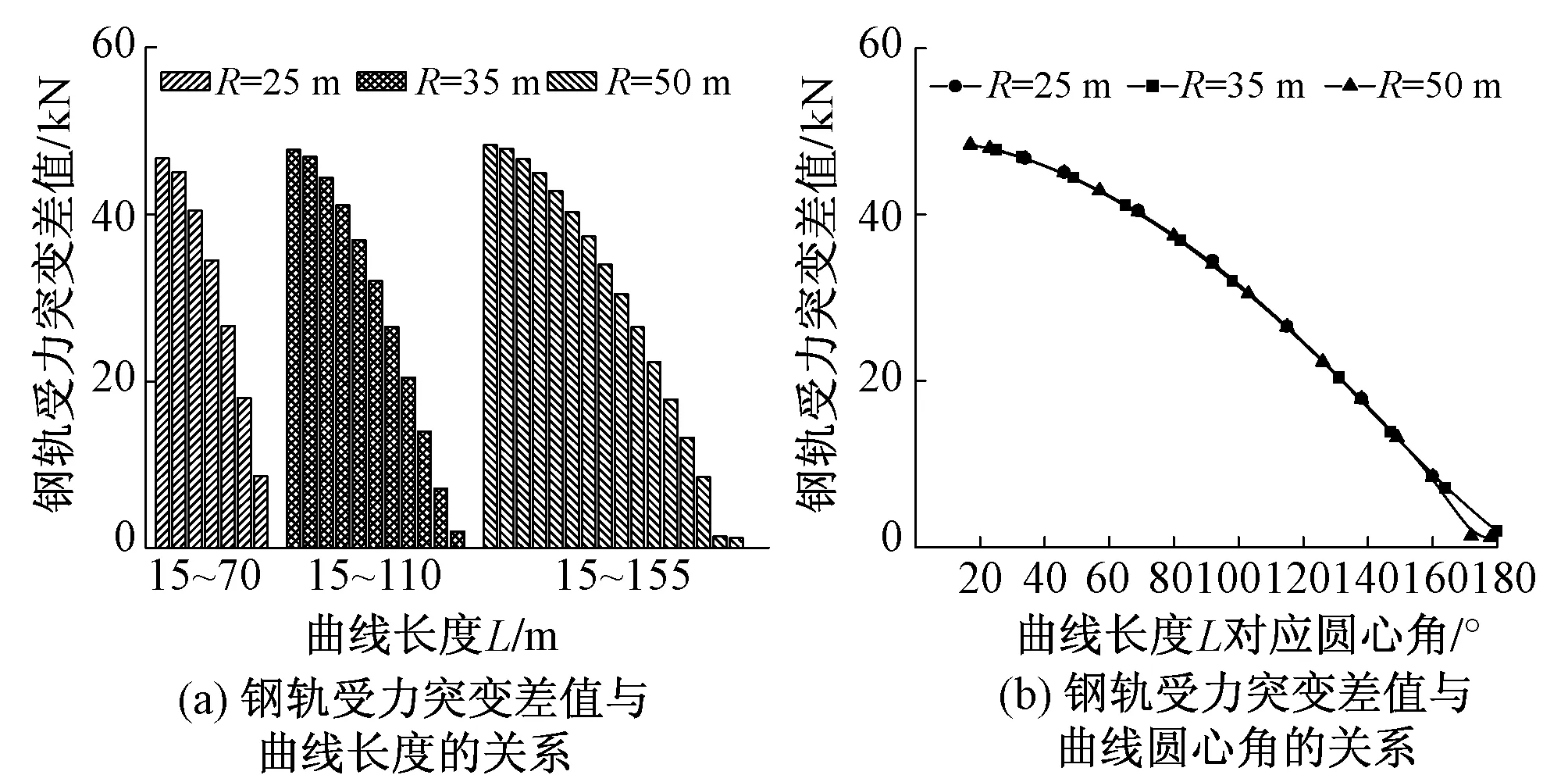
图4 常用荷载作用下钢轨受力突变差值
在排除钢轨温度、作用点等无关影响因素后,得到常用荷载组合作用时,钢轨受力突变差值随曲线半径、曲线长度的变化规律,如图4所示。由图4(a)可知,相同曲线半径时,钢轨受力突变差随曲线长度的增长而快速减小,曲线半径为35 m时,曲线长度为 110 m 时的钢轨受力突变差仅为曲线长度为15 m时的4%;曲线半径为50 m时,曲线长度为155 m时的钢轨受力突变差仅为曲线长度为15 m时的2%。由图4(b)可知,不同曲线半径下,钢轨受力突变差随着圆心角变化规律基本相同,随着圆心角的增大,钢轨受力突变差减小速度由慢变快,即曲线段圆弧长度对应圆心角较小时,列车横向荷载作用对钢轨受力影响较大,而对应圆心角较大时则影响较小,当对应圆心角达到或者接近180°时,已几乎没有影响。
由上述分析可知,轨道结构在常用荷载组合作用下,钢轨在列车横向荷载作用点两侧受力形成突变,其差值仅与曲线段圆弧长度对应圆心角有关,与钢轨温度、作用点、曲线半径无关。以上计算结果基于计算假定,未考虑轨道结构出现扣件失效等病害情况。为了降低列车通过小曲线半径时产生的横向力对轨道结构受力和变形的影响,可选用较大的圆心角。
3 结论
本文根据有轨电车交叉路口特小曲线半径段轨道结构特点,建立钢轨-道床三维空间耦合力学模型,在不同荷载工况作用下,得到轨道结构的受力和变形特性,结论如下:
1)轨道结构在最大温度荷载工况作用下,轨道结构未发生失稳破坏。小半径曲线段轨道结构向外臌曲变形,钢轨温度力得到释放。而直线段为无缝线路固定区,钢轨温度力无释放,在直圆点处容易受到直线段挤压而形成折角,其主要原因是曲率变化不连续。建议小半径曲线地段设置缓和曲线,有利于增强无缝线路稳定性。
2)轨道结构在最大温度荷载工况作用下,轨道结构整体横向位移较大,在钢轨与硬化铺装衔接处应采用可变形材料,以适应变形,防止挤压破坏。
3)轨道结构在最大温度荷载工况作用下,曲线对应圆心角小于90°时,温度力释放量快速增长;圆心角介于90°~150°时,温度力释放量增速放慢;超过150°时,温度力释放量出现一定的减少。
4)圆心角小于150°时,曲线半径越小,温度力释放量越小,这主要是由于曲线半径大所对应的线路长,其下部支承层为连续结构,在温度力作用下向外膨胀变形,会带动无缝线路横向位移和加大无缝线路温度力的释放。尽管小曲线半径对无缝线路受力和变形更有利,但会限制有轨电车允许通过速度,延长通过时间、影响交通,建议实际选线工作时,综合考虑曲线半径、允许通过速度、交通影响等因素。
5)轨道结构在常用荷载组合作用下,钢轨在列车横向荷载作用点两侧形成受力突变,其差值仅与曲线段圆弧长度对应圆心角有关,与钢轨温度、作用点、曲线半径无关。为了降低列车通过小半径曲线时产生的横向力对轨道结构受力和变形的影响,建议选用较大的圆心角。

