扣件失效对车-线-桥系统频率响应的影响

毛建红，张金喜，罗 俊

(1.北京工业大学 城市交通学院，北京 100124；2.中南大学 土木工程学院，湖南 长沙 410075)

随着我国轨道交通的快速发展，对轨道交通高架桥梁振动噪声问题的投诉也在不断增多[1-3]。为了降低桥梁的振动与噪声污染，各种减振器、隔振器以及减振轨道结构得到广泛应用，使用弹性扣件就是常用的措施之一。扣件大多利用橡胶垫层作为减振手段，但随着时间延长，橡胶弹性元件的耐久性和抗老化性有着不同程度的降低。而且随着列车循环往复的行驶，轨道结构受到很大的冲击，将导致扣件松脱或失效，这一问题随着线路运行密度的提高而更加严重。

我国学者针对扣件失效状态下轮轨系统的动力性能开展了研究。朱剑月[4]采用室内模型轨道，运用数值计算分析扣件支承失效对于轨道结构动力性能的影响。肖新标等[5-6]基于轮轨耦合动力学理论，从时域角度分析扣件失效工况下直线轨道和车辆系统的动态响应。张斌[7]运用基于车辆单元和轨道单元的车辆-轨道系统振动分析数值方法，研究了地铁扣件失效对轨道振动特性的影响。目前这些研究大多从时域角度分析扣件失效对轨道结构的影响，而很少从频域角度进行分析，而且扣件失效对桥梁结构的影响还鲜有研究。

鉴于此，本文基于车-线-桥耦合动力学理论，采用动柔度法建立车-线-桥耦合系统垂向振动的频域分析模型，详细分析了轨道正常、带有1个和3个失效扣件3种工况下车-线-桥系统的频率响应。

1 车-线-桥系统的频率响应

本文以城市轨道交通槽形梁为例，建立如图1所示的车-线-桥系统的垂向振动分析模型。车辆采用具有10个自由度的多刚体模型模拟，钢轨、桥梁分别采用无限长的Timoshenko梁和简支的Euler梁模拟，扣件系统和桥梁支座采用线弹性阻尼单元模拟，轮轨接触关系采用线性化的Hertz弹性接触理论。

图1 车-线-桥系统垂向振动模型

车辆系统的稳态响应为

(1)

式中：[MV]为车辆的质量矩阵；[CV]为车辆的阻尼矩阵；[KV]为车辆的刚度矩阵；{ZV(ω)}为车辆的位移向量；{P(ω)}为轨道不平顺引起的轮轨垂向相互作用力；ω为激振的圆频率。

根据动柔度定义，可得到车轮的动柔度为

(2)

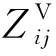
车轮动柔度可以写成一个4×4的矩阵

(3)

钢轨被视为无限长Timoshenko梁，其动柔度为[8]

βr(x1,x2)=u1e-ik1|x1-x2|+u2e-k2|x1-x2|

(4)

式中：βr(x1,x2)表示在钢轨上x2处施加单位谐荷载在x1处引起的位移；k1，k2，u1，u2为与振动波沿钢轨传播有关的参数。

利用动柔度的定义和叠加原理，钢轨在频域内的振动位移zr为

(5)

式中：Pw为第w个轮对施加在钢轨上xw处的垂向轮轨作用力；Nw为轮对数量；Ffn为第n个扣件施加在钢轨上xn处的扣件反力；N为1根钢轨下扣件的数量。

桥梁简化为简支的Euler梁，其稳态的振动响应可以表示为模态叠加形式，则简支Euler梁模型的动柔度βb可以表示为

(6)

式中：Wbn为简支梁的第n阶振型函数；ωbn为简支梁第n阶振型的固有频域；NMB为简支梁的计算模态数；ηb为桥梁的损耗因子。

利用动柔度的定义和叠加原理，槽形梁在频域内的振动位移zb为

(7)

式中：Fzh为第h个桥梁支座施加到桥梁上xh处的支座反力。

将式(5)和式(7)合并，可以写成矩阵形式：

[βK]{Z}={P}

(8)

式中：[βK]由钢轨和桥梁结构的动柔度乘以复刚度组成；{Z}由待求解的钢轨和桥梁结构的位移组成；{P}为荷载矩阵。

由式(8)可以求出轨道桥梁的动柔度为

(9)

与车轮动柔度相同，轨道桥梁的动柔度可以写成一个4×4的矩阵

(10)

因为频域分析模型只适用于线性系统，所以假定车轮和钢轨之间通过线性Hertz接触弹簧连接。轮轨接触刚度不仅与轮轨间的接触力、相对接触位移、材质的弹性系数有关，还与轮轨踏面形状有关[9]。轮轨接触弹簧的动柔度可以写成一个4×4的矩阵

(11)

式中：kc为线性化的轮轨接触刚度系数。

由于车轮模型轴距和定距的存在，不同轮轨接触点之间的激励出现时间滞后关系。图1模型中4个轮轨接触点的不平顺可表示为

R(t)={r1(t-t1)r2(t-t2)r3(t-t3)r4(t-t4)}T

(12)

式中：R为4个轮轨接触点的轨道不平顺；ri为第i个轮轨接触点轨道不平顺；t为时间;ti表示通过第i个轮轨接触点轨道不平顺的时间差，i=1,2,3,4。

假定t1=0，则车轮之间的时间差t2=2lt/V，t3=2lc/V，t4=2(lt+lc)/V。其中，V为车速，lt和lc分别为车轮轴距和定距的1/2。

假设时域的轨道不平顺为r(t)=r(ω)eiωt，则可得

(13)

以不平顺作为系统振动的激励源，由于车辆运行速度远小于振动波在钢轨中传播的速度，采用移动不平顺模型误差很小。假定车轮与轨道桥梁相对位置不变，而不平顺以一定速度在车轮与钢轨之间移动，以此形成相对位移激励。则动态轮轨作用力Pwr可表示为

Pwr=-(βV+βTB+βc)-1R(ω)

(14)

将求出的轮轨作用力代入式(1)和式(8)，即可求出车辆、钢轨和桥梁结构频域的动力响应。

2 计算参数

2.1 车辆、轨道、桥梁参数

地铁车辆以A型车为例，其参数见表1。

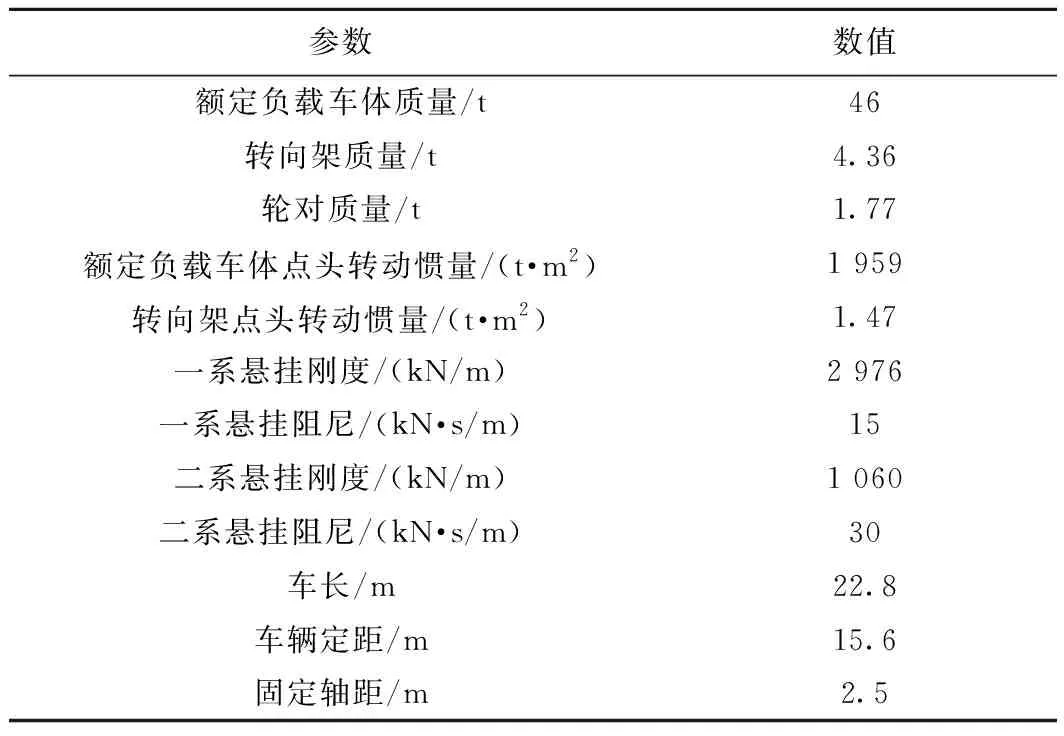
表1 地铁A型车的计算参数

桥梁选用应用广泛的城市轨道交通槽形梁，轨道、桥梁的结构参数见表2。

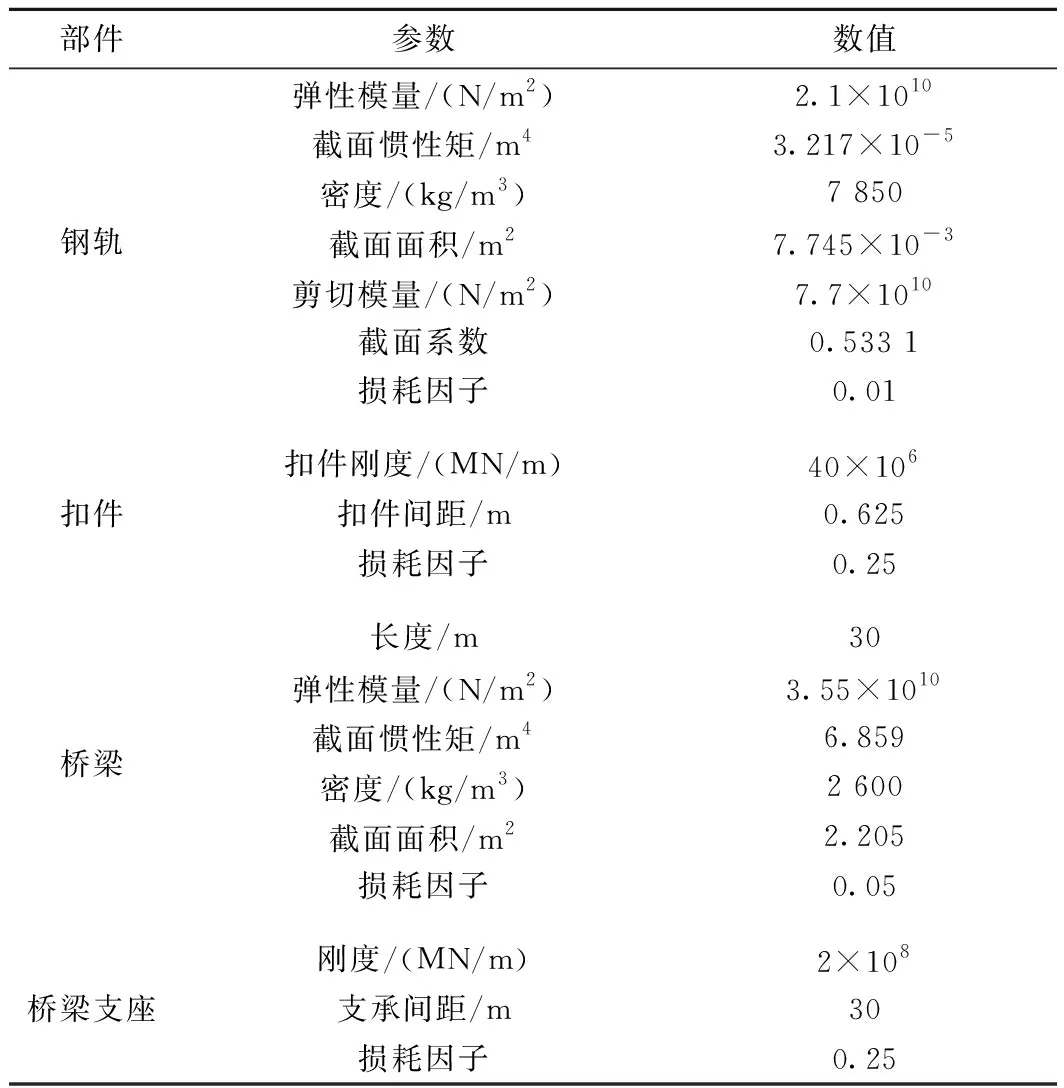
表2 轨道、桥梁的计算参数

2.2 轨道不平顺

车辆速度取80 km/h，轨道不平顺选用标准GB/T 5111—2011《声学 轨道机车车辆发射噪声测量》中以图表方式给出的0.63 m以下各个中心波长的频域幅值，经拟合得到表达式为

(16)

式中:r0为参考粗糙度值，r0=10-6m；λ为1/3倍频程中心波长。

2.3 扣件失效工况

应用上述模型，分析扣件失效对车-线-桥耦合系统频率响应的影响。本文考虑扣件失效时为完全失效，即令扣件刚度为0。工况1，2，3分别代表无扣件失效、跨中1个扣件失效和跨中3个相邻扣件失效。

3 扣件失效对耦合系统频率响应的影响

本文选取车体垂向振动加速度、钢轨垂向振动加速度、桥梁垂向振动加速度和扣件支反力4个动力学指标进行分析。计算结果见图2—图5。

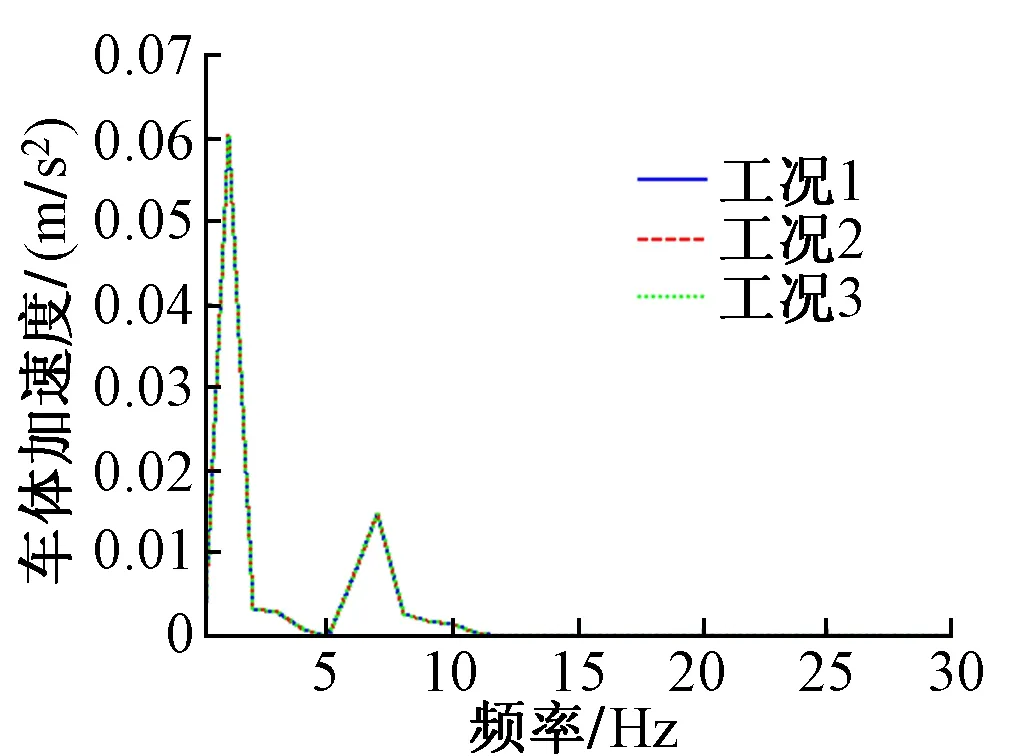
图2 车体垂向振动加速度

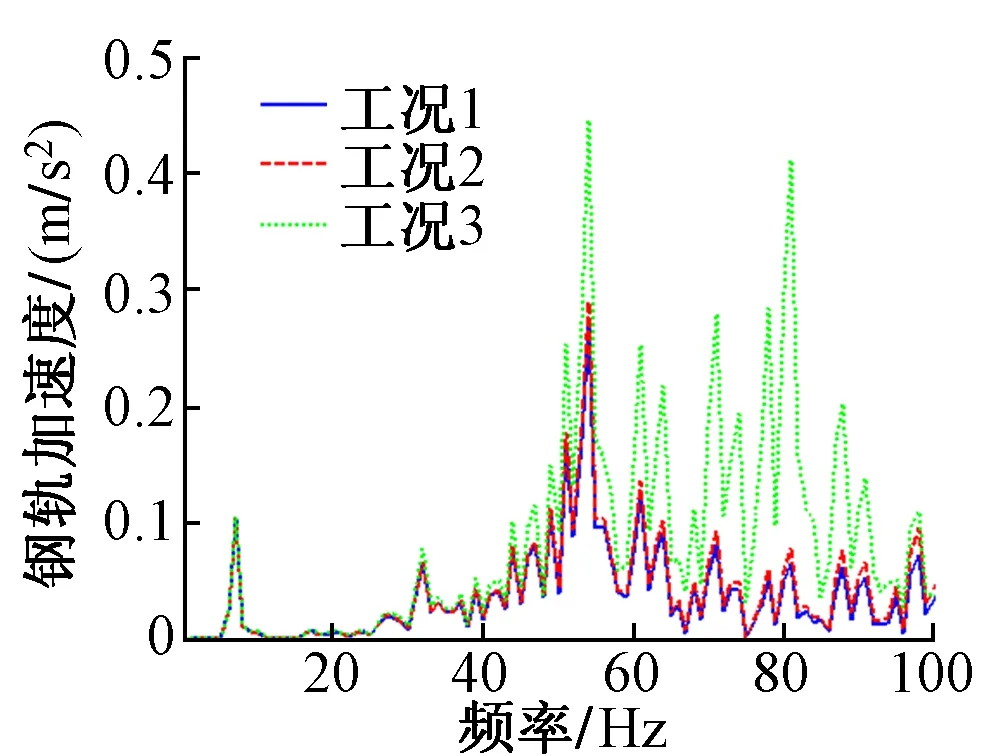
图3 钢轨垂向振动加速度

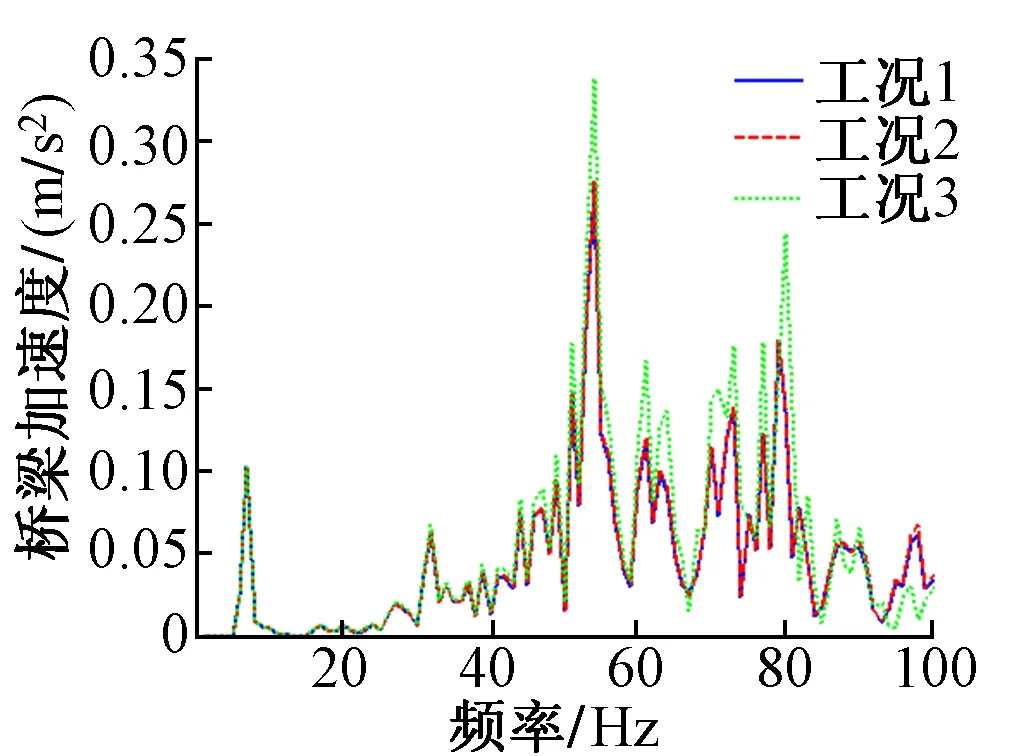
图4 桥梁垂向振动加速度

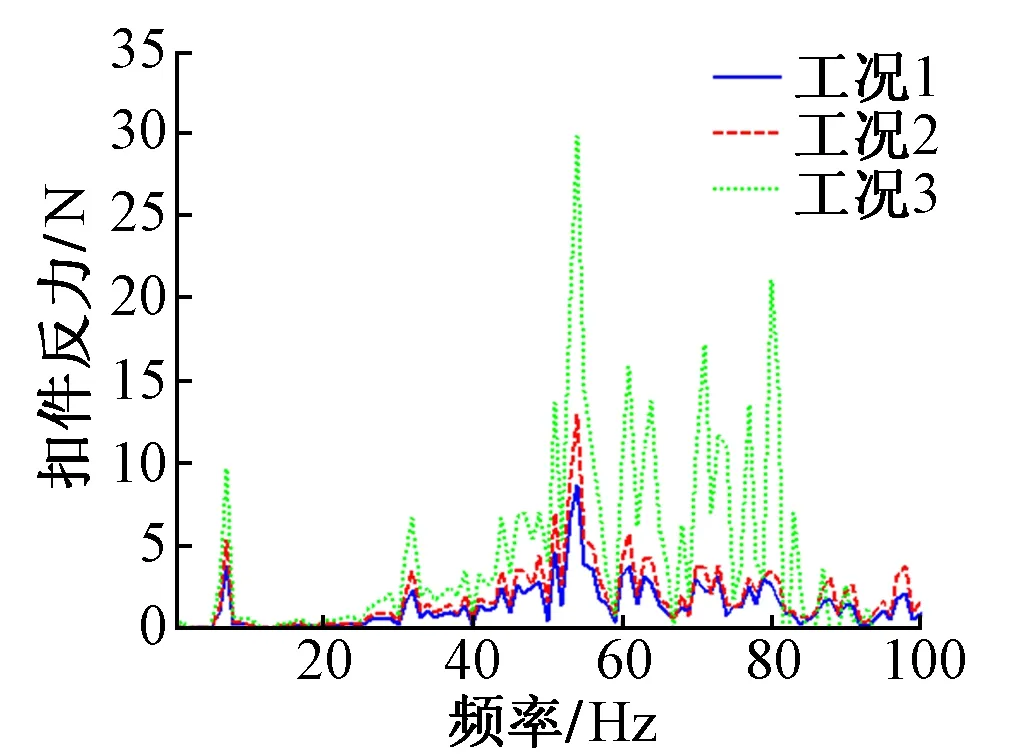
图5 相邻扣件支反力

图2为车体的垂向振动加速度。可知，3条曲线基本重合，而且第一主频都在1 Hz处。说明扣件失效对车体振动加速度的影响很小，这可能是由于一、二系悬挂系统削弱了扣件失效对车体振动的影响。这和文献[10]得出的结果相吻合。

图3为钢轨的垂向振动加速度。可知，扣件失效时，钢轨振动的主频并没有发生改变，但钢轨振动加速度会增大。而且随着扣件失效数增大，钢轨在频率50～80 Hz内的振动加速度急剧增大。当有3个扣件失效时，钢轨的振动加速度增长了65%。

图4为桥梁的垂向振动加速度。可知，扣件失效时，桥梁振动的峰值频率并没有改变，且与轮轨耦合共振频率一致，但其最大值略有增加。而且随着扣件失效数量增多其幅值也在增大。

图5为相邻扣件的支反力。可知，扣件失效时会使相邻扣件的支反力增大。而且随着扣件失效数量增多，相邻扣件的支反力会急剧增大。这表明当出现扣件失效时，容易引起相邻扣件的破坏。

综上所述，由于一、二系悬挂系统的存在，扣件失效时对车体振动加速度影响很小，但是对钢轨的冲击和相邻扣件的支反力影响较大。这容易造成相邻扣件产生累积变形，加速扣件的老化，极易使相邻扣件也失效，从而产生连锁反应，危及行车安全。

4 结论

本文基于车-线-桥耦合动力学理论，运用动柔度法建立了车-线-桥垂向耦合振动的频域分析模型，讨论了扣件失效对车-线-桥耦合系统频率响应的影响，得到如下结论：

1)扣件失效对车体振动加速度的影响很小。

2)扣件失效对钢轨振动加速度影响较大，且其影响随着失效扣件数的增加而增大。但对桥梁振动加速度的影响比钢轨要小一些。

3)扣件失效使相邻扣件支反力显著增大，且支反力随着扣件失效数的增加而增大。如不及时处理，会造成连锁反应，加剧线路的不平顺，影响行车安全。

4)工务部门应加强对扣件失效现象的检查，一旦发现，应立即采取措施予以消除。