时速350 km高速铁路40 m跨度预应力混凝土简支箱梁徐变上拱控制设计研究
苏永华,石 龙,胡所亭,班新林,杨心怡
(1.中国铁道科学研究院集团有限公司 铁道建筑研究所,北京 100081;2.高速铁路轨道技术国家重点实验室,北京 100081)
铁路预应力混凝土简支梁在施加预应力和梁体恒载共同作用下,各截面处于偏心受压状态,截面混凝土压应力沿梁高呈线性变化,下翼缘压应力较大,上翼缘压应力较小,甚至会出现拉应力。由于混凝土具有徐变特性,在预应力产生的反弯矩长期荷载作用下,梁体产生上拱变形,即预应力简支梁的徐变上拱[1]。我国高速铁路桥梁普遍为标准跨度预应力混凝土简支箱梁,大量采用无砟轨道形式。由于梁体徐变上拱,轨道铺设完成后桥上线路会形成连续周期性高低不平顺[2],引起了相关高铁运营部门的重视。
我国既有标准简支箱梁常用跨度为24 m和 32 m,基于2016年度中国铁路总公司重大课题——《高速铁路大跨度简支梁建造关键技术研究》相关成果可知,中国铁道科学研究院集团有限公司已完成跨度40 m标准简支箱梁的科研与设计。目前国内院校及科研单位对常用跨度简支箱梁徐变上拱问题有一定研究[3-5],然而对更大跨度简支箱梁未有相关成果,且未有对残余徐变上拱的控制方法进行系统研究。
本文系统地开展40 m跨度简支箱梁残余徐变上拱(即轨道铺设完成后的残余徐变上拱量)控制方法研究,在全预应力范围内分析降低跨中底缘压应力、提高预应力合力中心高度、缩短底板预应力束长度、增加梁高、提高混凝土强度等级、推迟二期恒载上桥时间、细化二期恒载分级等方法降低残余徐变上拱的效果及适用性,进一步确定40 m跨度箱梁残余徐变上拱控制措施,达到指导桥梁设计与施工的目的。
1 40 m跨度简支箱梁关键参数
1.1 结构形式及预应力布置
综合考虑车桥动力响应、运输架设条件、梁体受力特点、构造布置要求等因素,时速350 km高速铁路40 m 简支箱梁的梁长取40.6 m,计算跨度取39.3 m;采用单箱单室形式,轨下箱梁截面高度为3.235 m。40 m 跨度简支箱梁截面如图1所示,截面预应力布置如图2所示。采用全预应力体系设计,腹板单排布束,其中底板预应力束(N1a,N1b,N2a~N2d)竖弯倾角为4°,腹板预应力束(N3~N6)竖弯倾角为6°,且设置平弯。梁体混凝土为C50级。
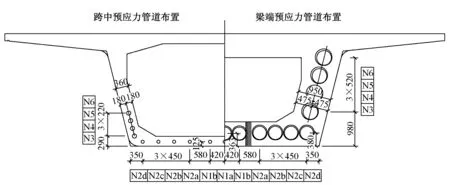
图2 40 m跨度简支箱梁截面预应力布置(单位:mm)
1.2 主要受力及变形指标
40 m跨度简支箱梁主要受力及变形指标见表1。可知:
1)在不同二期恒载等级下,梁体跨中底缘压应力、抗裂安全系数、强度安全系数等受力指标均满足规范要求;梁体静活载挠跨比、梁端转角、竖向基频等变形指标均满足规范要求。
2)参照既有通用图设计,考虑二期恒载施加时间在终张拉后60 d,不同二期恒载等级下40 m跨度箱梁残余徐变上拱值均超过7 mm,且二期恒载等级越低,残余徐变上拱越大。40 m梁残余徐变上拱值最大为8.73 mm,较既有32 m跨度无砟箱梁5.8 mm和24 m跨度无砟箱梁2.4 mm大[6-7],且跨度越大,残余徐变上拱值越大。
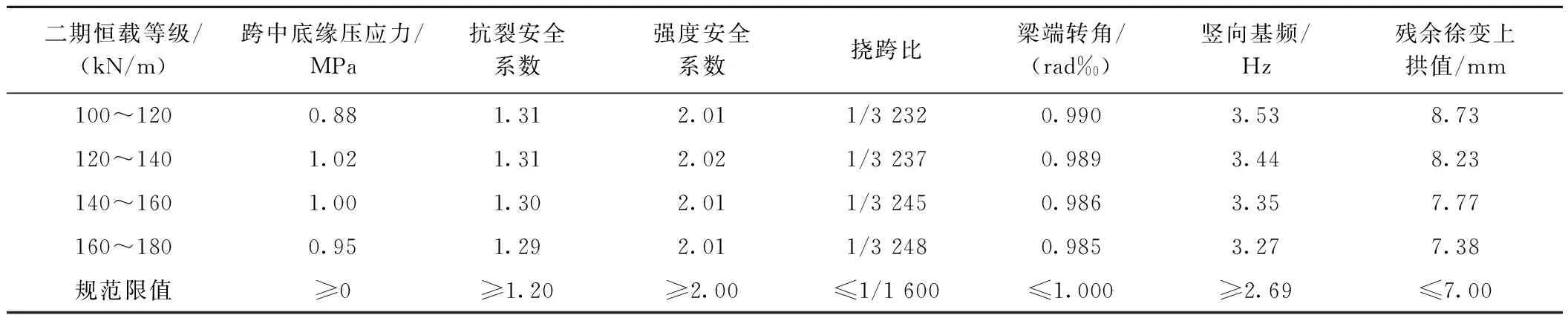
表1 40 m跨度简支箱梁主要受力及变形指标
注:表中受力及变形指标均给出最不利值;残余徐变上拱值以终张拉后60 d施加二期恒载计算,对于无砟轨道,规范限值为10 mm,考虑变异系数一般需控制在7 mm及以下。
2 残余徐变上拱控制方法分析
本节在全预应力体系范围内系统研究控制箱梁残余徐变上拱的方法,并给出40 m跨度梁残余徐变控制措施的合理建议。
2.1 降低跨中底缘压应力
箱梁预应力设计时会考虑一定安全余量,使主力荷载作用下跨中截面底缘存在1.0 MPa左右的压应力[6-7]。本文分析在全预应力情况下,适当降低跨中底缘压应力对减小残余徐变上拱的影响,并探讨其可行性。鉴于残余徐变上拱在最低二期恒载等级下最大,分析时主要考虑二期恒载等级为100~120 kN/m的情况。
不同跨中底缘压应力下的残余徐变上拱值见表2,残余徐变上拱值与跨中底缘压应力关系曲线见图3。

表2 不同跨中底缘压应力下的残余徐变上拱值

图3 残余徐变上拱值与跨中底缘压应力关系曲线
由表2和图3可知:
1)随着跨中底缘压应力降低,梁体残余徐变上拱值近于线性减小(相关系数R>0.999 9);压应力每减小0.1 MPa,残余徐变上拱值降低0.169 mm。
2)跨中底缘压应力由0.88 MPa降低至0.12 MPa 时,残余徐变上拱值由8.73 mm降低至7.45 mm,仍在7 mm 以上。
3)如果残余徐变上拱值控制在7 mm以内,那么主力荷载下跨中底缘将承受0.15 MPa的拉应力,梁体处于部分预应力状态。
综上可知,在全预应力体系范围内,降低40 m跨度箱梁跨中底缘压应力,不能将其残余徐变上拱值控制在7 mm 以内;张拉时管道内钢绞线有所上浮,跨中底缘压应力会减小0.2 MPa左右;考虑施工中各方面因素与设计状态的偏差,底缘压应力需预留一定的余量。因此,不宜通过降低跨中底缘压应力的方式来降低残余徐变上拱。
2.2 提高预应力合力中心高度
简支箱梁预应力设计时,预应力合力中心尽可能偏低以达到提高预应力效率、减少钢绞线用量的目的。然而,预应力合力中心过低会使梁体反向弯矩增加,梁体徐变上拱变大[8]。本节研究提高预应力合力中心高度对降低40 m跨度箱梁残余徐变上拱的影响,主要考虑3种方案:①增强腹板预应力并减弱底板预应力;②加大腹板预应力束间距;③顶板纵向张拉预应力束。同时,3种方案均控制梁体跨中底缘压应力使其与原设计相当。
2.2.1 增强腹板预应力并减弱底板预应力
在截面预应力位置不变(参见图2)、跨中底缘压应力相近的条件下,通过调整钢绞线根数、增强腹板预应力并减弱底板预应力,可提高预应力合力中心高度。不同钢绞线根数分配下的残余徐变上拱值见表3。

表3 不同钢绞线根数分配下的残余徐变上拱值
注:计算时各预应力束张拉控制应力与原设计保持一致。
由表3可知:
1)随着腹板预应力增强与底板预应力减弱,梁体残余徐变上拱值逐渐减小,N3~N6各腹板束每增加1根钢绞线,残余徐变上拱值平均减小0.13 mm左右。
2)方案3中腹板束采用34根钢绞线、底板束采用5或6根钢绞线,梁体残余徐变上拱值可降至7 mm左右,此时钢绞线用量相比原设计增加6.2%。
3)采用方案3时,由于腹板预应力增强较大,导致预应力终张拉时梁端箱内上下倒角及进人孔倒角处出现较大的主拉应力(超过9 MPa),增加了梁端开裂风险。
因此,采用增强腹板预应力并减弱底板预应力的方式控制梁体残余徐变上拱是不合理的。
2.2.2 加大腹板预应力束间距
在图2中跨中截面腹板预应力束间距为220 mm,满足规范构造要求的最小间距[9]。在保持预应力梁端位置不变、各腹板束起弯点纵向位置不变、N3束跨中高度不变、跨中底缘压应力相近的条件下,通过增加跨中截面N3~N6腹板预应力束的间距,可提高预应力合力中心高度。不同腹板预应力束间距下的残余徐变上拱值见表4。

表4 不同腹板预应力束间距下的残余徐变上拱值
由表4可知:
1)随着腹板预应力束间距的增加,梁体残余徐变上拱值降低,但钢绞线用量增加。
2)腹板预应力束间距增加至580 mm时,梁体残余徐变上拱值可降至7.19 mm,但钢绞线用量相比原设计增加了12.4%(大于二期恒载160 ~180 kN/m的钢绞线用量),预应力效率明显降低。
3)预应力配束的增加会使终张拉时梁端各倒角的局部应力变大,增加开裂风险。
因此,采用加大腹板预应力束间距的方式控制梁体残余徐变上拱也是不合理的。
2.2.3 顶板纵向张拉预应力束
在箱梁顶板纵向张拉2束N7预应力束,也可提高预应力合力中心高度。顶板张拉纵向预应力束方案见图4。

图4 顶板张拉纵向预应力束方案(单位:mm)
设计N7预应力束为直线束,距梁底高度为3 m,沿梁全长布置,横向位于梁端腹板中心线处,锚外张拉控制应力 1 340 MPa(与N3~N6束相同)。调整各预应力束的钢绞线根数,保证跨中底缘压应力接近原设计值。计算结果表明,每一N7束钢绞线根数为19根及以上时,梁体残余徐变上拱值可降至7 mm以内,但存在如下不足:①N7预应力束在梁端锚固空间较为紧张,且会增大预应力张拉时梁端各部位局部应力,增加梁端开裂风险;②为使残余徐变上拱值在7 mm以内,张拉N7束会使预应力钢绞线总用量增加13%以上(大于二期恒载160 ~180 kN/m的钢绞线用量),预应力效率明显降低。
因此,采用箱梁顶板纵向张拉预应力束的方式控制梁体残余徐变上拱也是不合理的。
2.3 缩短底板预应力束长度
为使梁体箱内构造简洁及预应力张拉施工方便,既有铁路标准箱梁的预应力束均沿梁体全长布置,并锚固于梁端[6-7]。这种布束方法,虽然满足了箱梁跨中截面压应力的要求,但会造成1/4跨至梁端区域存在较大的压应力冗余。采取措施减小压应力冗余可有效降低梁体残余徐变上拱。
考虑腹板预应力束存在一定倾角,能有效抵抗受剪区域的剪应力(对于40 m箱梁,受剪区的范围和剪力均较32,24 m箱梁大),因此本节根据40 m梁底板预应力布置方案,仅缩短部分底板预应力束的长度,将原通长的N1a,2N2a,2N2c共5束预应力束的长度缩短至20 m,并锚固于箱内1/4跨的底板顶面,其余预应力束保持不变。同时,通过配置合适的预应力筋使主力荷载下跨中截面压应力与原设计值相同。缩短部分底板预应力束示意如图5。

图5 缩短部分底板预应力束示意(单位:mm)
计算结果表明:
1)箱梁各截面压应力、抗裂安全系数、强度安全系数、剪应力、主应力等指标均满足规范要求。
2)与原设计值相比,梁体残余徐变上拱值由8.73 mm 降至6.91 mm,在7 mm以内。
3)钢绞线用量为13.049 t,与原设计值相比减少10.3%。
综上可知,缩短箱梁部分底板预应力束,在满足受力要求的情况下可降低梁体残余徐变上拱、减少钢绞线用量。然而,因需在箱内预留锚固尺块,且对预应力张拉工作带来较大不便,缩短部分预应力束的方式在现浇梁中可以应用,但在基于预制架设模式的简支箱梁中未曾采用。40 m跨度预制箱梁不推荐采用此种方式降低残余徐变上拱。
2.4 增加梁高
在梁重变化不大的情况下,增加梁高可提高梁体截面抗弯惯性矩,降低跨中残余徐变上拱。本节以图1中截面为基准,设计高度分别为3.335,3.435,3.535,3.635,3.735 m时的40 m跨度箱梁,调整预应力以保证主力荷载下跨中底缘压应力相近,梁体残余徐变上拱值见表5。可知:
1)随着梁高的增加,梁体残余徐变上拱值降低;梁高每增加10 cm,残余徐变上拱值降低0.35~0.38 mm;梁高为3.735 m时,梁体残余徐变上拱值可降至7 mm以内。
2)梁高由3.235 m增加至3.735 m时,跨中截面积增加3.7%,而抗弯惯性距增加38.4%。

表5 不同梁高下的残余徐变上拱值
注:跨中截面积与跨中抗弯惯性距为毛截面对应参数。
残余徐变上拱值与跨中截面抗弯惯性矩关系曲线见图6。可知抗弯惯性距与残余徐变上拱值近于线性相关(相关系数R>0.999)。
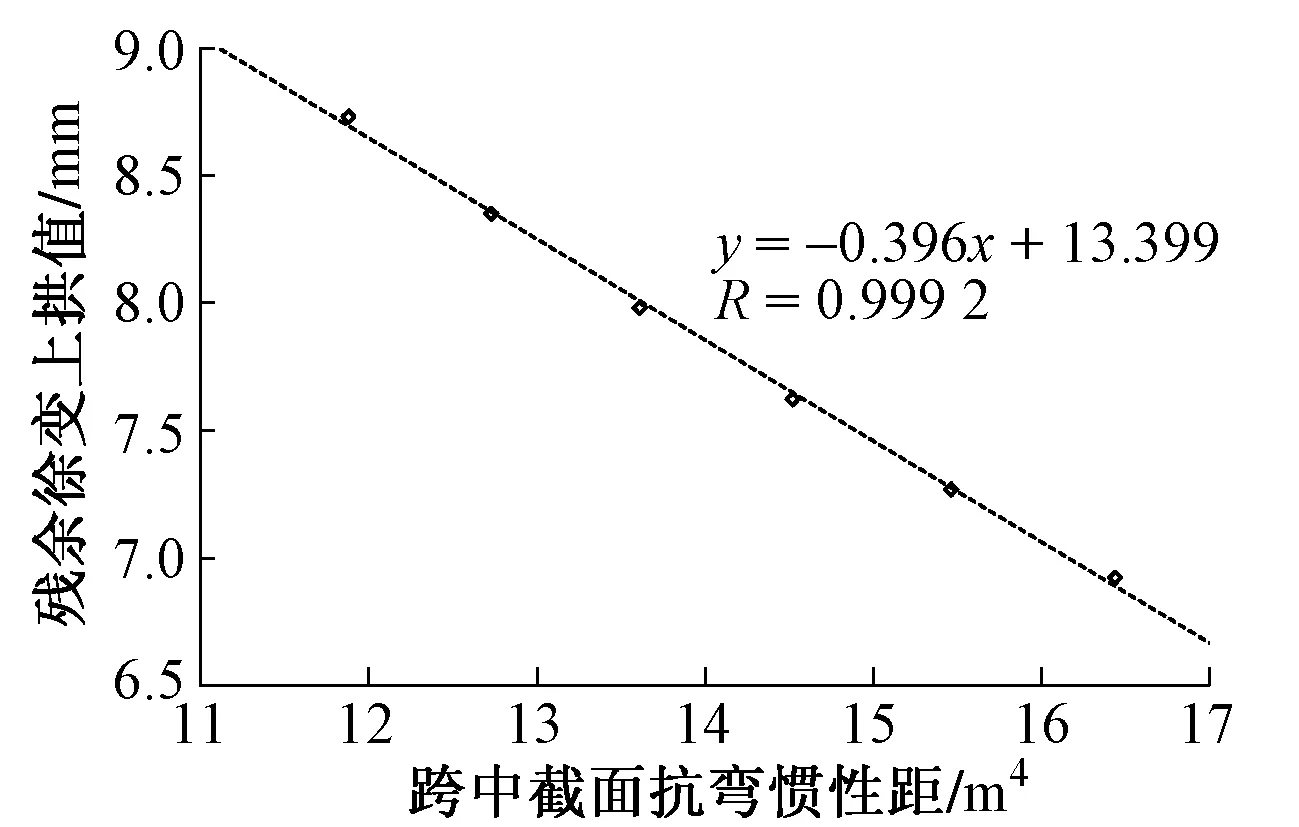
图6 残余徐变上拱值与截面抗弯惯性矩关系曲线
综上可知,增加梁高可有效提高截面抗弯惯性距,降低残余徐变上拱。对于预制架设的40 m跨度箱梁来说,梁高需增加至3.7 m以上,与既有现浇40 m跨度箱梁高度相当[10]。考虑预制箱梁运梁过隧道工况,梁高为3.235 m时过隧空间已较为紧张,梁高增至3.7 m将无法实现运梁过隧。因此40 m跨度预制箱梁不推荐采用增加梁高的方式来降低残余徐变上拱。
2.5 提高混凝土强度等级
若提高混凝土强度等级,其弹性模量会有所增加,则徐变上拱降低。不同混凝土等级下40 m跨度箱梁的残余徐变上拱值见表6。
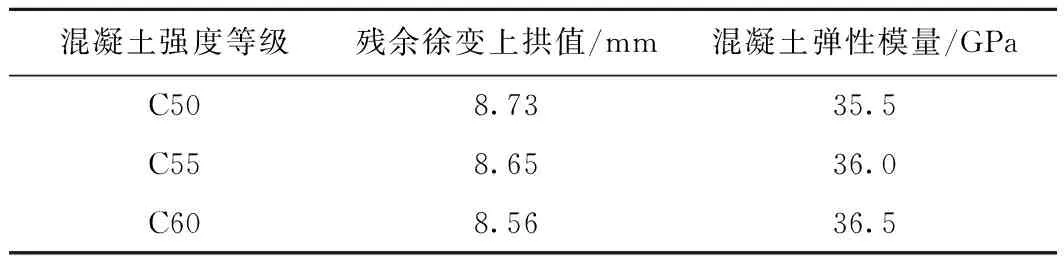
表6 不同混凝土等级下40 m跨度箱梁的残余徐变上拱值
由表6可知:
1)混凝土强度等级由C50变为C60,梁体残余徐变上拱值降低2.0%,相应混凝土弹性模量提高2.8%,二者比例接近。
2)采用C60级混凝土,梁体残余徐变上拱值为8.56 mm,超过7 mm限值。
因此,提高混凝土强度等级对降低梁体残余徐变上拱的效果不明显。
2.6 推迟二期恒载上桥时间
推迟二期恒载上桥时间,使二期恒载上桥前梁体徐变上拱尽可能地发展,从而可减小二期恒载上桥后梁体的残余徐变上拱。表7给出40 m梁不同二期恒载上桥时间下的残余徐变上拱值,图7为其相应关系曲线。由表7和图7可知:
1)推迟二期恒载上桥时间可明显降低梁体残余徐变上拱。
2)二期恒载上桥时间在终张拉后75 d时,梁体最大残余上拱值即可降低至7.43 mm;二期恒载上桥时间在终张拉后90 d,梁体最大残余徐变上拱值可控制在6 mm左右,小于7 mm。

表7 不同二期恒载上桥时间下的残余徐变上拱值
注:二期恒载上桥时间以终张拉完成时间起算。
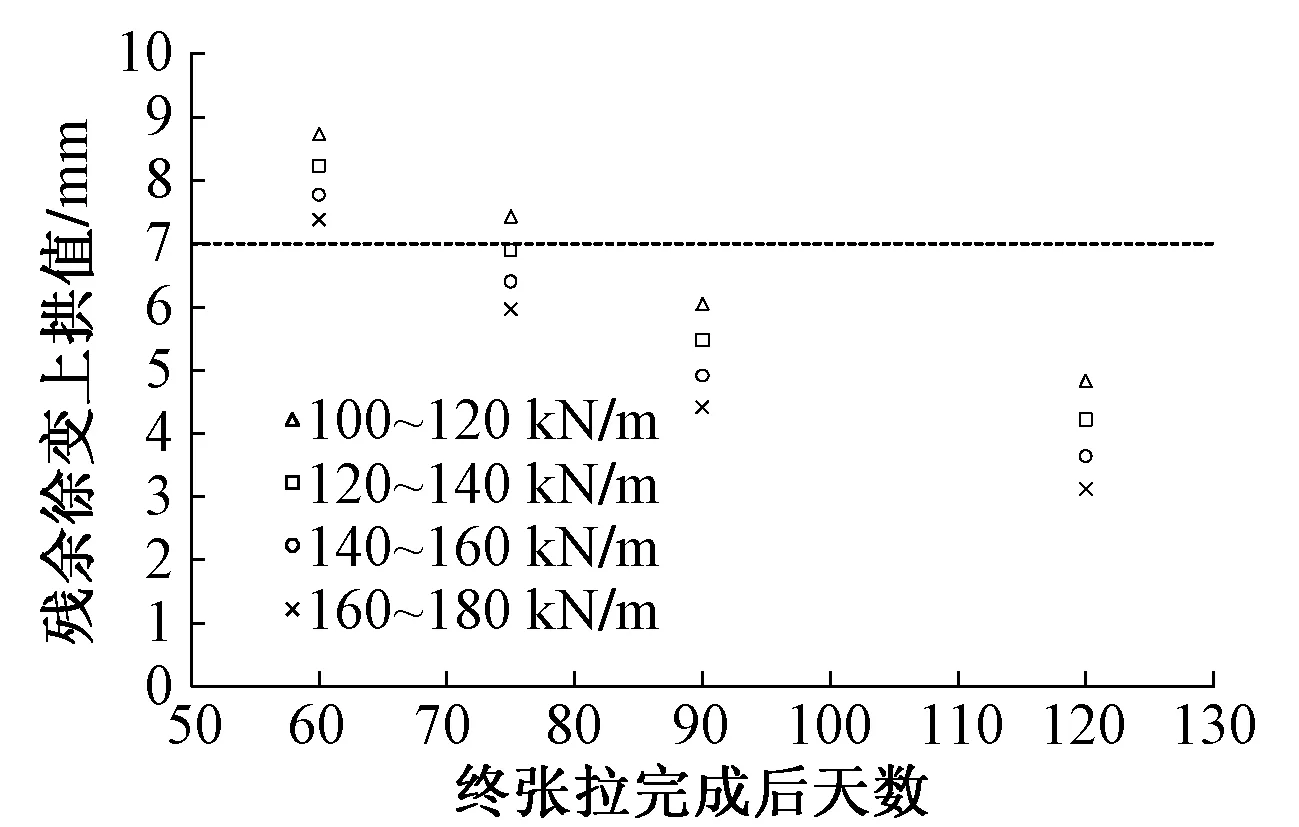
图7 残余上拱值与二期恒载上桥时间关系曲线
目前高铁箱梁设计二期恒载上桥时间为终张拉后60 d,而实际中受制梁情况、运架条件等影响,往往有所推迟。故40 m跨度箱梁考虑将二期恒载上桥时间推迟至75 d,并结合其他措施将梁体最大残余徐变上拱值控制在7 mm左右。
2.7 细化二期恒载分级
高铁箱梁的预应力以二期恒载大小为分级依据,无砟箱梁以20 kN/m为级差。以100~120 kN/m为例,其预施应力需满足120 kN/m二期恒载的受力要求,而当实际梁体二期恒载为100 kN/m时,跨中残余徐变上拱值即出现最大值。因此,40 m跨度箱梁考虑将二期恒载分级细化,以10 kN/m为级差,使梁体预应力设计、降低残余徐变上拱更精细化。细化后的二期恒载等级适用桥梁属性见表8。

表8 细化后的二期恒载等级适用桥梁属性
40 m跨度箱梁细化分级后二期恒载上桥时间在终张拉后75 d时的跨中残余徐变上拱值见表9。可知,细化分级后40 m跨度箱梁最大残余上拱值为7.02 mm,总体上满足要求。
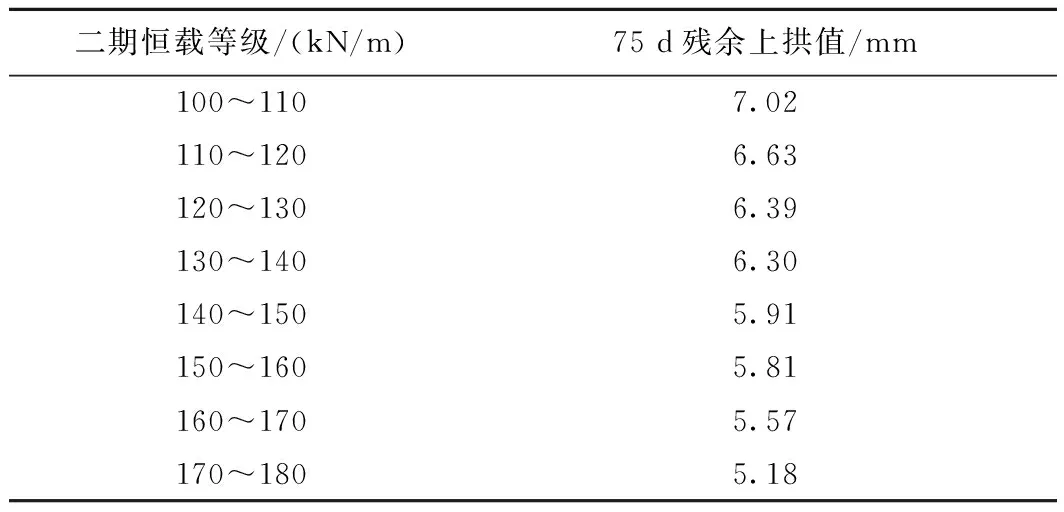
表9 细化二期恒载分级后的残余徐变上拱值
综上所述,最终确定40 m跨度箱梁应同时采用推迟二期恒载上桥时间为终张拉后75 d和细化二期恒载分级2种方法来控制其残余徐变上拱值。
3 结论
1)简支箱梁跨度越大,残余徐变上拱越大,对于40 m跨度简支箱梁,残余徐变上拱为设计控制指标。
2)降低跨中底缘压应力、提高预应力合力中心高度、增加梁高、提高混凝土强度等级等方法可不同程度地降低梁体残余徐变上拱,但受各方面因素限制,在40 m跨度箱梁设计时不宜采用。
3)缩短部分底板预应力束的方法可有效降低40 m 跨度箱梁残余徐变上拱,但不便于箱梁施工,在少量现浇梁中可考虑采用,在大量使用的预制梁中不宜采用。
4)采用推迟二期恒载上桥时间为终张拉后75 d和细化二期恒载分级2种方法,可有效控制40 m跨度箱梁残余徐变上拱。

