铁路常用跨度简支箱梁桥新型支撑体系减震性能研究
曹志峰,臧晓秋,石秋君,孙明德
(1.中国铁道科学研究院集团有限公司 铁道建筑研究所,北京 100081;2.高速铁路轨道技术国家重点实验室,北京 100081)
常用跨度简支箱梁桥是铁路桥梁结构中最简单、应用最多的结构形式,尤其是在大规模的高速铁路和城际铁路建设中。因此,结构中一些细微的改进就有可能带来很大的经济效益[1-2]。
常用跨度简支箱梁桥主要由梁体和墩台及其支撑体系构成,支撑体系是梁体和墩台之间关联部件的总称,具有承受并传递竖向荷载和水平荷载、适应梁端位移和转角的作用。传统支撑体系由桥梁支座和防落梁挡块组成,由于桥梁支座和防落梁装置不具有耗能功能,因此在地震作用下只能通过桥墩延性抗震。对于重力式桥墩来说,由于桥墩本身刚度很大,难以出现塑性铰,因此无法采用延性设计方法,一旦发生超出设计地震烈度的强烈地震,结构几乎不可避免地会遭到严重损伤甚至破坏。支撑体系是影响桥梁结构受力状态的主要因素,因此本文进行了铁路常用跨度简支梁桥新型支撑体系的研究。该支撑体系除具有传统支撑体系的全部功能外,还具有耗能减震作用。其主要特点是将简支箱梁桥梁体和墩台两端的“固定-活动”约束转变为弹塑性约束,可显著改善墩台受力,有效提高结构抗震能力[2-4]。
本文采用动力仿真方法,选择跨度40 m高速铁路预应力混凝土简支箱梁桥为研究对象,对简支箱梁桥新型支撑体系的减震性能进行研究。
1 新型支撑体系的组成及受力特征
1.1 新型支撑体系的组成
新型支撑体系在组成上与传统支撑体系的不同之处在于该体系是由桥梁支座和阻尼装置组成,其中桥梁支座均为多向活动支座。该体系组成如图1所示。
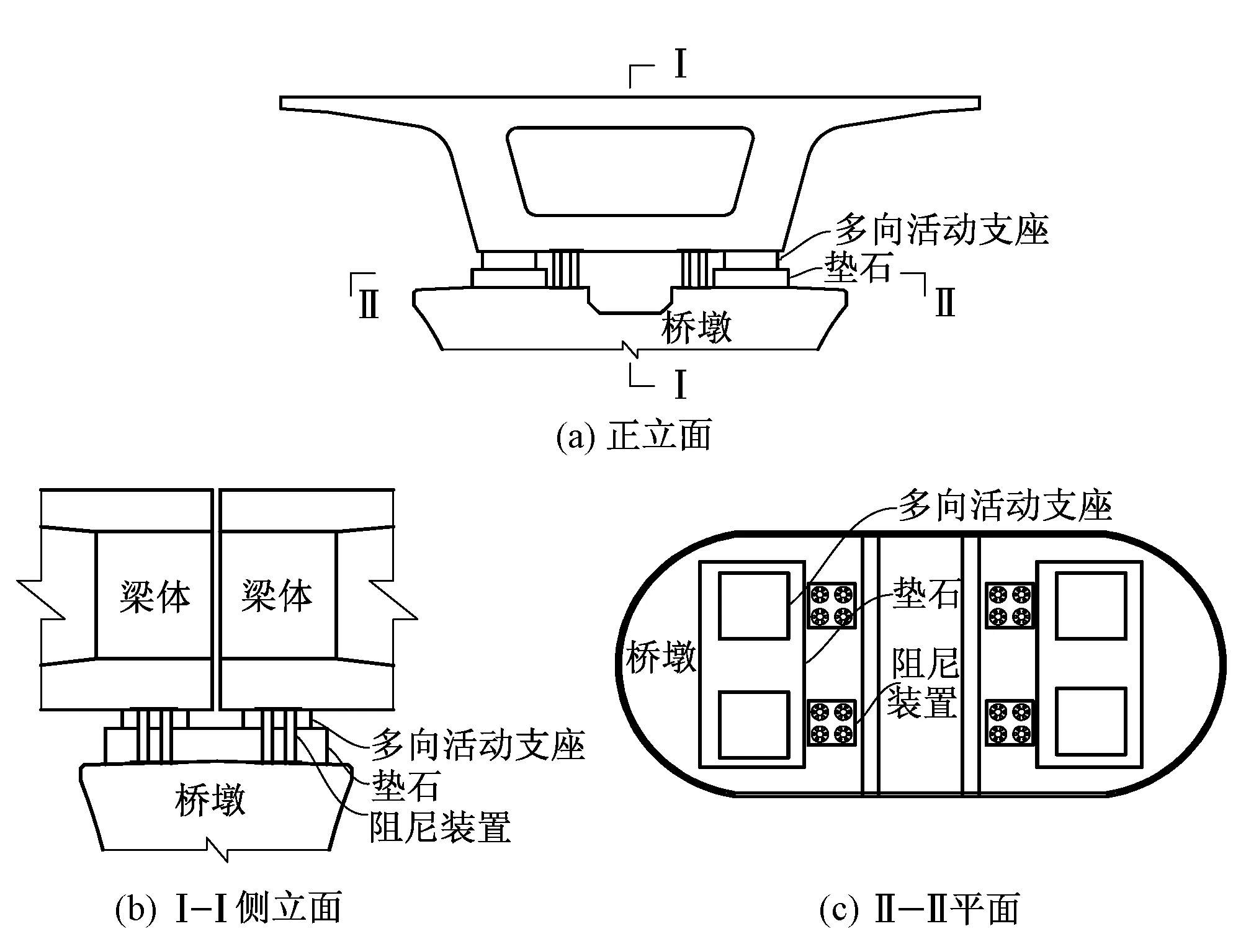
图1 新型支撑体系组成示意
1.2 新型支撑体系的受力特征
新型支撑体系与传统支撑体系相比,特点在于其实现了支座水平力的传递与竖向支承功能的完全分离,梁体传来的竖向荷载仍由支座承担,而梁体的水平荷载则由阻尼装置承担。其最显著的受力特征是梁体水平向约束状态的改变,由传统支撑体系的“固定-活动”约束(见图2(a))转变为新型支撑体系的弹塑性约束(见图2(b))。
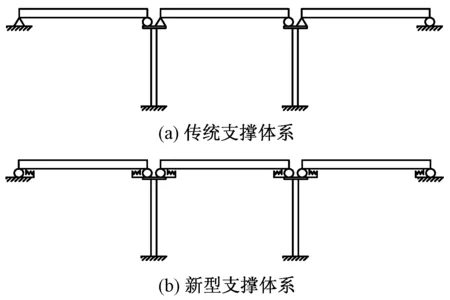
图2 2种支撑体系约束状态示意
2 新型支撑体系设计原则
根据新型支撑体系的组成和受力特征可以看出阻尼装置并不只是在结构受到地震作用时提供额外刚度和阻尼的附加装置,同时也是承担梁体运营期间水平荷载的重要构件,在整个支撑系统中起着至关重要的作用。因此,新型支撑体系设计的关键是阻尼装置的设计。现有的阻尼材料有速度相关型和位移相关型2种,根据新型支撑体系对于阻尼装置的性能要求,本文选用位移相关型阻尼材料——软钢。软钢拉伸时的应力-应变曲线(见图3)可分为4个阶段:弹性阶段(OA)、屈服阶段(AB)、强化阶段(BC)和破坏阶段(CD)。设计时依据刚度配置合理和阻尼约束有效的原则。
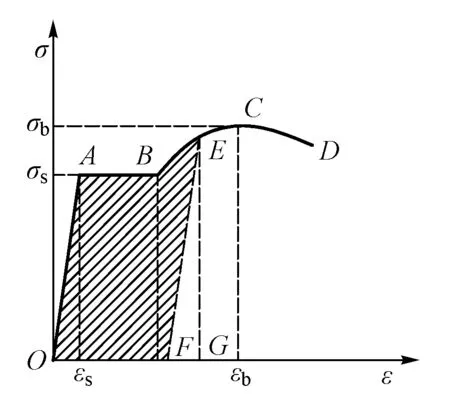
图3 软钢拉伸应力-应变曲线
2.1 刚度配置合理
由于新型支撑体系中阻尼装置是承担结构水平荷载的重要构件,因此通过精细化设计与制造,使阻尼装置在正常运营荷载下以及多遇地震作用下处于弹性工作区间。由软钢的拉伸应力-应变曲线(参见图3)可知,日常运营荷载以及多遇地震作用下阻尼装置的应力段应位于OA区间。
2.2 阻尼约束有效
为保证阻尼约束的有效性,首先要选择塑性阶段长、耗能能力强的钢材,其次设计时应该合理选择工作应变范围,在保证安全的前提下充分利用材料。显然,进入塑性阶段后阻尼装置的主要工作应变范围为应力平台段(图3中AB段),因此所选软钢材料的应力平台越长越好。
3 算例
3.1 工程概况
我国铁路简支箱梁桥常用跨度为24,32,40 m,随着桥梁跨度的增加,地震作用下落梁和支座破坏问题会更加突出。因此,本文选择跨度40 m高速铁路预应力混凝土简支箱梁桥为研究对象。梁体为双线整孔简支箱梁,桥墩为双线圆端形实心桥墩,墩高取10 m。桥址处抗震设防烈度为8度,场地特征周期为0.45 s,设计地震动峰值加速度为0.3g,多遇地震动峰值加速度为0.1g,罕遇地震动峰值加速度为0.57g。
3.2 新型支撑体系设计
本文选用具有等强度特性的短刚臂钢棒阻尼器作为阻尼装置[5-6](见图4)。短刚臂钢棒阻尼器结构设计主要分为2个部分:AB段和BC段。其中AB段为直线,BC段为等强度抛物线,且AB,BC相切于B点。AB段的长度为L1,总长为L。B点所在平面圆的直径为d0,BC段x点所在平面圆的直径为d(x)。短刚臂钢棒阻尼器的设计参数见表1。
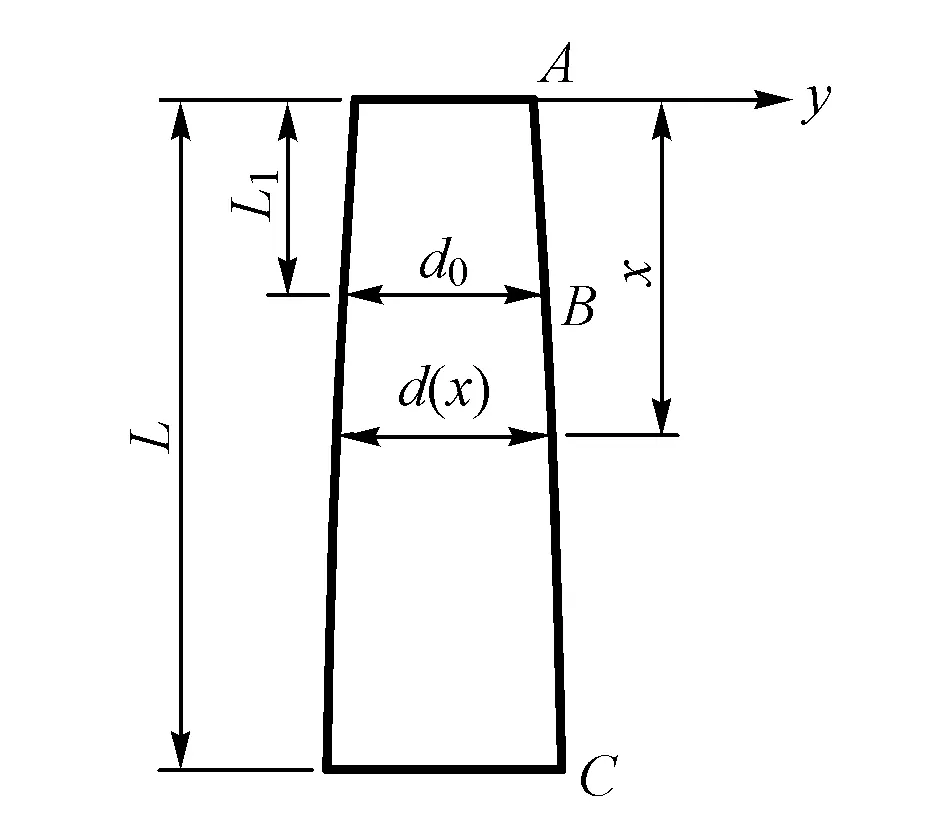
图4 短刚臂钢棒阻尼器主体结构形式

设计水平力/kN设计位移/mm极限位移/mm阻尼比屈后刚度比150160 200 0.450.07
基本设计思路是:
第1步。计算运营荷载和多遇地震作用下阻尼装置的刚度需求量,从而确定新型支撑体系的最低刚度,据此确定所需短刚臂钢棒阻尼器的数量。
第2步。设计地震作用下的结构抗震性能,目的是确定设计地震作用下新型支撑体系抗震性能是否满足要求,如满足要求则进入第3步,如不满足要求则从第1步重新开始。
第3步。在罕遇地震作用下对结构进行安全性能评估,目的是判断罕遇地震作用下新型支撑体系是否会发生落梁。评估的标准是阻尼装置位移是否超过极限位移,如满足要求则设计完成,如不满足要求则从第1步重新开始。
从上述设计思路中可以看出,短刚臂钢棒阻尼器设计的首要问题是刚度设计。短刚臂钢棒阻尼器和桥墩为串联刚度体系,其合成刚度k为
式中:k1为阻尼装置刚度;k2为桥墩刚度。
合成刚度应满足以下要求:
1)运营荷载作用
为满足运营荷载作用下桥上无缝线路的稳定性、安全性及梁体横向变形要求,纵横向刚度应符合以下规定[7]。①纵向刚度,根据TB 10002—2017《铁路桥涵设计规范》,对于跨度40 m混凝土简支梁,当不做梁-轨共同作用分析时,墩台顶纵向水平线刚度不宜小于550 kN/cm。②横向刚度,由TB 10002—2017中无砟轨道桥梁相邻梁端两侧的钢轨支点横向相对位移不应大于1 mm以及墩顶横向力的相关规定来确定。
2)多遇地震作用
多遇地震刚度需求主要是为了满足小震不坏的抗震设计原则,要求多遇地震作用下短刚臂钢棒阻尼器为弹性状态。可根据桥址处多遇地震下峰值加速度、梁体和二期恒载重量采用静力法进行计算。
3.3 分析计算
3.3.1 分析模型
模型假定:①桥梁上部结构和桥墩在地震作用下保持线弹性;②不考虑基础和地基的影响,墩底按固结处理;③不考虑桥面系对桥墩的纵向约束作用;④不考虑活动支座摩擦力;⑤阻尼装置的力学性能是单个阻尼器力学性能的线性叠加。
建立有限元模型时,桥墩和箱梁均采用线性梁单元模拟,活动支座、阻尼装置对应的约束条件采用主从关系处理。有限元分析模型如图5所示。阻尼装置采用双线性恢复力模型,如图6所示,其中,Fy为最大弹性力,即设计水平力;Fu为最大屈服力,即水平极限承载力;d1为最大弹性位移;d2为最大屈服位移,即设计位移;Ku为弹性刚度,Ku=Fy/d1;Kd为屈服后的刚度;Kd/Ku为屈后刚度比。本文算例一孔梁选取16根短刚臂钢棒阻尼器构成4组阻尼装置。

图5 有限元分析模型

图6 阻尼装置双线性恢复力模型
3.3.2 地震动输入
结构动力反应不但与结构特性有关,还与输入的地震波密切相关。本文根据GB 50111—2006《铁路工程抗震规范》给出的动力放大系数曲线,采用三角级数法作为拟合方法,编制了人工地震波模拟程序[8-11],随机模拟的人工地震波时程及动力放大计算系数与规范给定的动力放大目标系数对比见图7。

图7 人工地震波时程及计算系数与目标系数对比
3.4 计算结果
3.4.1 设计地震
分析时考虑2种工况:工况1为传统支撑体系,梁体与桥墩之间采用球型支座连接;工况2为新型支撑体系,梁体与桥墩之间通过阻尼装置与多向活动支座共同连接。随机模拟3条符合规范要求的设计地震波(0.3g)作为地震动输入。表2—表5分别为2种工况下3条设计地震波激励下1#墩、2#墩墩底受力情况及其平均减震率。减震率=(工况1墩底剪力平均值-工况2墩底剪力平均值)/工况1墩底剪力平均值。
3.4.2 罕遇地震
以3.4.1节工况2的新型支撑体系为评估对象,随机模拟3条符合规范要求的罕遇地震波(0.57g)作为地震动输入。
图8—图10分别为3种罕遇地震波激励下梁端典型1组(4根)阻尼装置的滞回曲线。可知,3种地震波激励下阻尼装置均充分进入塑性变形阶段,滞回曲线饱满,且阻尼装置的最大位移依然处于设计位移内,远小于极限位移。

表2 地震作用下各工况墩底纵向剪力

表3 地震作用各工况墩底横向剪力

表4 地震作用下各工况墩底纵向弯矩

表5 地震作用下各工况墩底横向弯矩

图8 罕遇地震波1作用下阻尼装置滞回曲线

图9 罕遇地震波2作用下阻尼装置滞回曲线
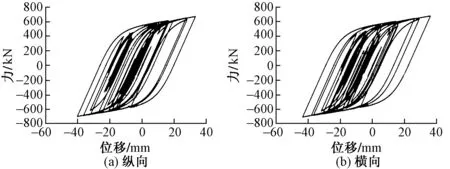
图10 罕遇地震波3作用下阻尼装置滞回曲线
4 结论
本文选择跨度40 m高速铁路预应力混凝土简支箱梁桥为研究对象,并建立有限元模型进行计算分析,得到如下结论:
1)设计地震作用下,新型支撑体系可显著改善桥墩受力,本文算例中墩底弯矩和墩底剪力的减震率均在77%以上。
2)罕遇地震作用下,新型支撑体系可起到防落梁作用,本文算例中阻尼装置在罕遇地震作用下最大位移小于其极限位移,可充分保证地震时梁体的安全。
3)在选择合适的阻尼材料,并经过合理的刚度设计后,新型支撑体系在地震发生时可提供较大的塑性变形以发挥耗能减震作用,从而有效地提高了简支箱梁桥结构的抗震能力。

