基于犹豫模糊群决策模型的云计算服务商选择

刘 俊

常州大学 信息科学与工程学院，江苏 常州 213164

1 引言

多属性群决策问题是现实生活中普遍存在的问题，也是决策领域经常研究的问题之一[1-3]。由于决策问题具有复杂性、不确定性等特征，很难用精确清晰的数字来描述这些决策问题的属性[4-6]。Zadeh[7]提出的模糊集能较好地处理描述模糊信息。但是随着模糊集的发展，学者们发现其存在一定的不足，于是模糊集的各类型拓展形式依次被提出和研究，包括：区间模糊集[8]、直觉模糊集[9]、模糊粗糙集[10]、Type-2模糊集[11]等等。作为模糊集的一种有效扩展，Torra[12]引入了犹豫模糊集，其中单位元是由0和1之间的不同的隶属度构成，因此犹豫模糊集能够有效处理其中的数据是不确定的或决策者可能决定有犹豫的情况。

多属性群决策问题的一个重要部分就是如何构建合理有效的模糊信息集成算法来选出最优方案[13-14]。文献[15]利用算术平均，提出了几类新的直觉模糊信息集成算子用于对属性值进行集成。文献[16]建立了三种直觉模糊信息集成算子方法。Wei[17]将优先算子提出了犹豫模糊优先算术加权平均算子和犹豫模糊优先几何加权平均算子，并将提出的算子应用于教师招聘过程中。针对Wei[17]中算子存在的不足，文献[18]提出了两个具有幂等性和有界性的改进犹豫模糊集成算子，并将它们应用到实际案例问题中。Xu和Xia[19]详细研究了犹豫模糊信息的相似度、距离和相关度，同时提出了犹豫模糊信息集成算子的决策模型。文献[20]在直觉模糊正态环境下构建了一种基于信息集成算法的多属性决策模型。

Maclaurin对称平均最初是由麦克劳林[21]提出的，其可以反映多个输入变量之间的相互关系，同时Maclaurin对称平均相对于参数单调递减，使得决策者可以根据其偏好选择合适的参数值进行决策。另一方面，上述所有信息集成算子都是基于代数范数提出的，而代数范数只是Archimedean范数的一种特殊运算[17]。因此，有必要研究基于Maclaurin对称平均和Archimedean的犹豫模糊糊信息集成算法，使得决策者对信息集成方法的选择性更多、涵盖范围更广。本文首先基于Maclaurin对称平均和Archimedean范数定义了犹豫模糊MSM算子，研究了其具有的优良性质和常见形式，最后基于犹豫模糊加权Maclaurin对称平均算子构建了犹豫模糊多属性群决策模型，并通过云计算服务商选择实例论证了其有效性和可行性。

2 基本概念和理论

2.1 概率犹豫模糊集

定义1[12]令X={x1,x2,…,xm}为一个给定的集合。形如H={＜xi,h(xi)＞|xi∈X}的二元组称为X上的犹豫模糊集（Hesitant Fuzzy Set，HFS）。其中，h(xi)={γi|γi∈h(xi)}是由若干组实数组成的集合，γi表示元素 xi属于集合H的可能隶属度。为了方便起见，称hi=h(xi)为一个犹豫模糊元（Hesitant Fuzzy Element，HFE）。

由于犹豫模糊元中的元素可以通过β-标准化方法进行增加，因此为了下面计算的方便，规定本文犹豫模糊元中元素个数均为l，即h={γ(k)|k=1,2,…,l}，其中γ(k)表示h中的第k大元素。

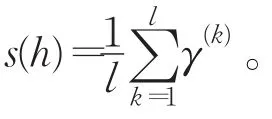
分析发现，现有的代数乘法和加法运算只是Archimedean范数中的一种形式，严格Archimedean T-范数可由一个严格单调递减的加性算子g:[0,1]→[0,+∞]表示为T(x,y)=g-1(g(x)+g(y))，其中g(1)=0,g(0)=1。根据对偶原则，严格Archimedean S-范数可表示为S(x,y)=f-1(f(x)+f(y))，其中 f(t)=g(1-t)，于是 f(t)严格单调递增，且 f(0)=0,f(1)=1[22]。

接下来，介绍运用Archimedean范数定义犹豫模糊元之间新的运算法则。

定义3 设j=1,2，为三个HFE，定义如下运算：

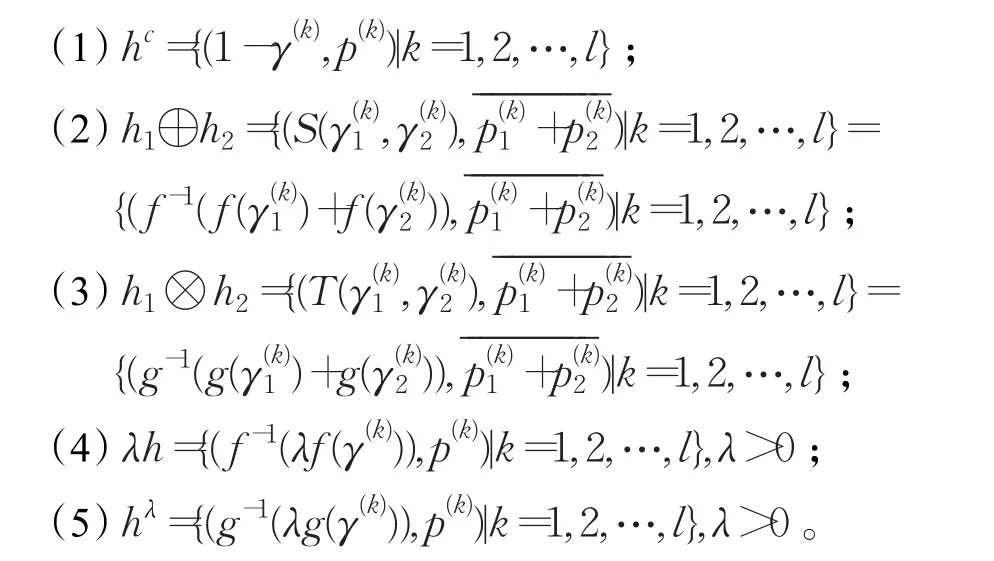
从定义3可知，通过新的运算法则计算得到的犹豫模糊元中元素个数仍是l。容易证明，定义3中的运算满足如下性质。

定理1 令j=1,2，为三个HFE，则有：

2.2 Maclaurin对称平均

定义4[21]令a1,a2,…,an是一组非负实数，并且r=1,2,…,n 。如果

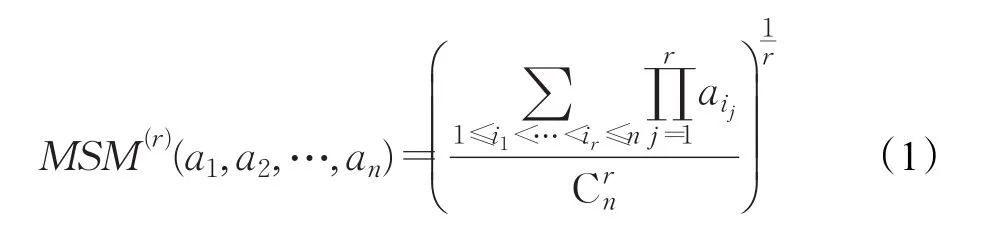
3 HFMSM算子及其性质和常见形式

本章主要将Maclaurin对称平均引入到犹豫模糊环境下，提出HFMSM算子，然后分别研究HFMSM算子所具备的优良性质和一些特例。

3.1 HFMSM算子

定义5令hi(i=1,2,…,n)是一列犹豫模糊元，且r=1,2,…,n。如果

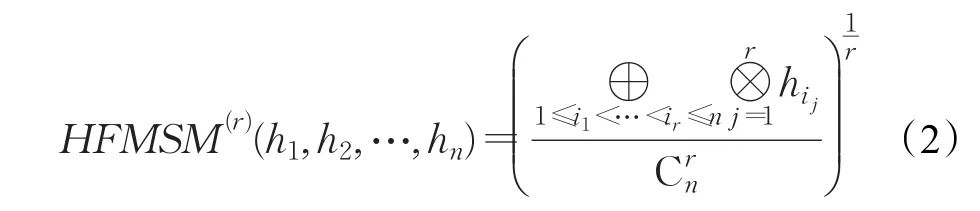
称为犹豫模糊Maclaurin对称平均算子，简记为HFMSM(r)算子。

定理2令hi(i=1,2,…,n)为一列HFE，则运用HFMSM(r)算子得到的集成结果仍为HFE，且有：

证明（1）根据定义4中的运算法则，可得：

于是有：

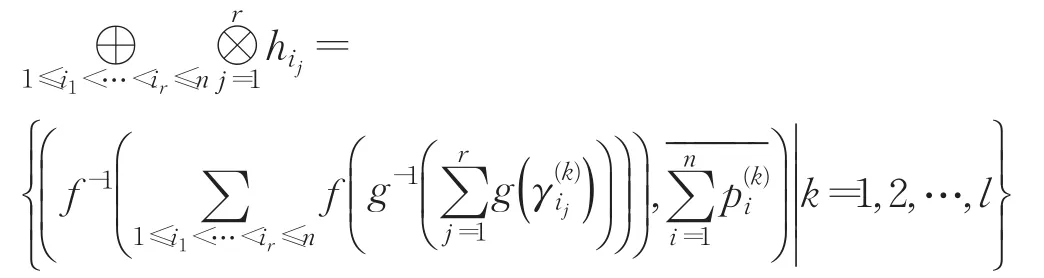
所以

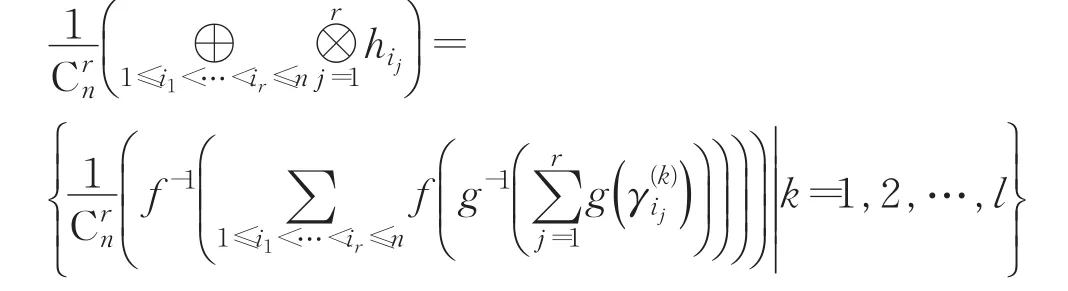
从而，集结结果为：

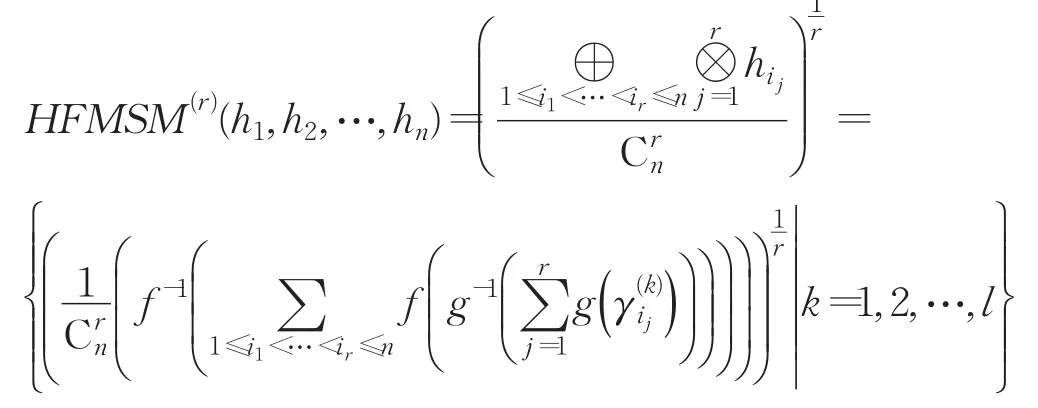
所以公式（2）成立。

（2）若要证明HFMSM(r)算子得到的结果仍为HFE，即证对任意的k=1,2,…,l，有：

又因 f(t)和 f-1(t)为严格单调递增函数，则

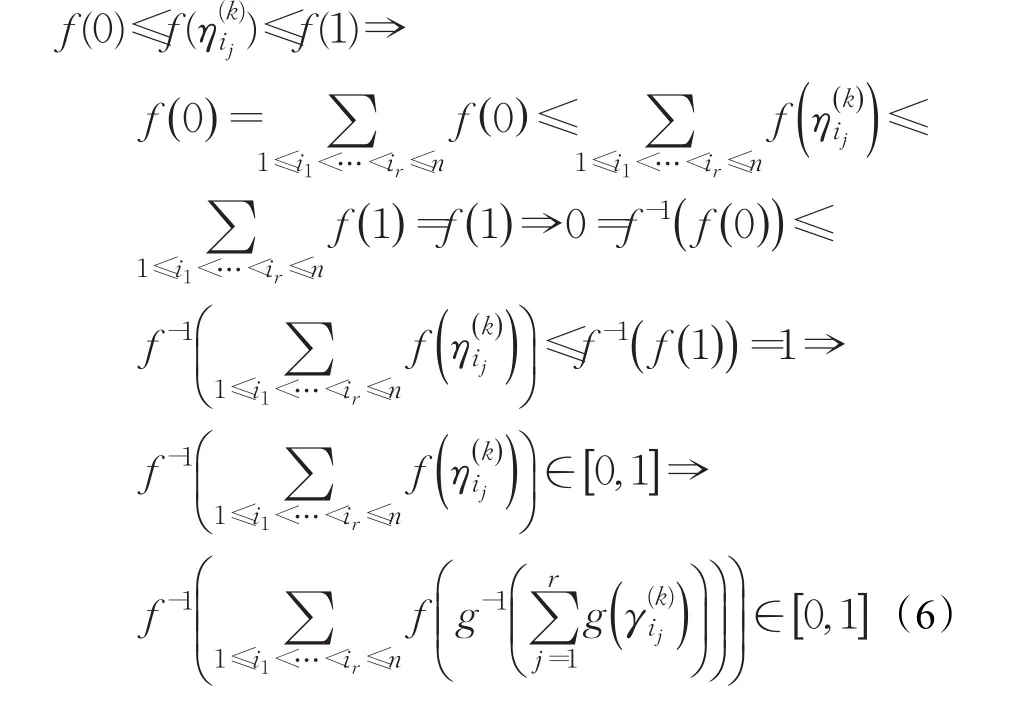
综上证明过程可知，运用HFMSM(r)算子得到的结果仍为HFE。因此，定理2成立。

3.2 HFMSM算子的基本性质

性质1（置换不变性）令hi(i=1,2,…,n)为一列HFE，如果是的一个任意置换，则有：

证明因为是 {h1,h2,…,hn}的一个任意置换，则根据定义5可得：

因此，性质1成立。

性质2（幂等性）令hi(i=1,2,…,n)为一列HFE，如果对于所有的i=1,2,…,n，都有hi=h={r}，则

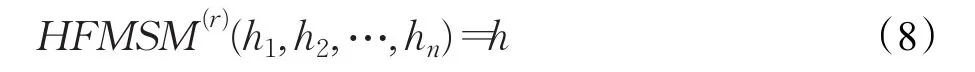
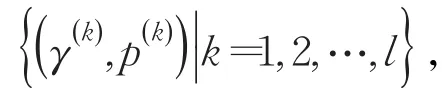
综上，易知性质2成立。

性质3（单调性）假设和 ai=为两列PHFE。若对任意的k=1,2,…,l，i=1,2,…,n有，那么

证明因为，然后根据函数 g(t)、g-1(t)、f(t)和 f-1(t)的单调性，可得：

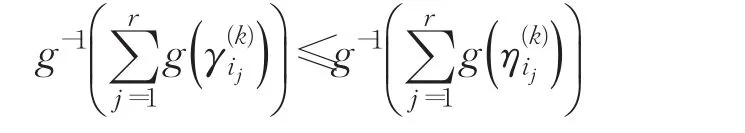
于是

所以有：

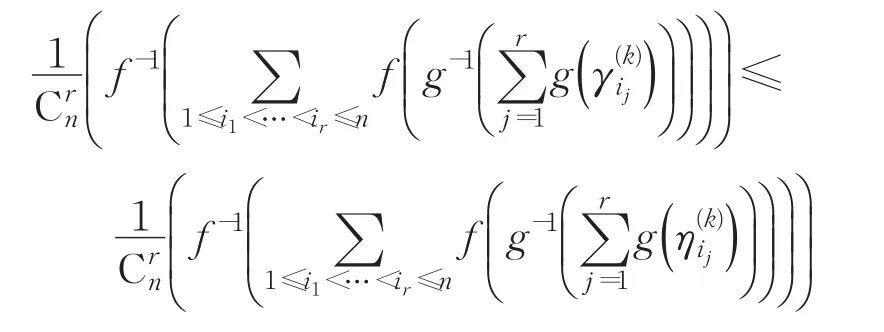
从而得到下面的不等式：

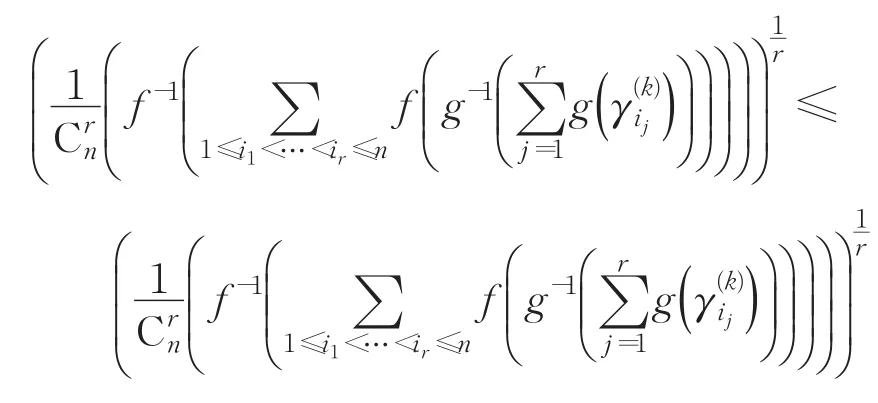
即公式（9）成立。

结合性质2和性质3，容易证明性质4成立。

性质4（有界性） 假设为一列HFE，令l}，则有：

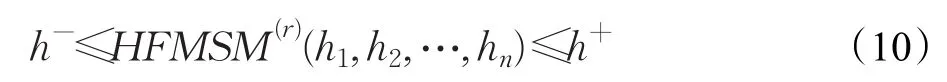
3.3 HFMSM算子的几类特例

本节将介绍HFMSM()r在参数r取不同值时的特殊形式。

情形1当r=1时，HFMSM()r转化为：

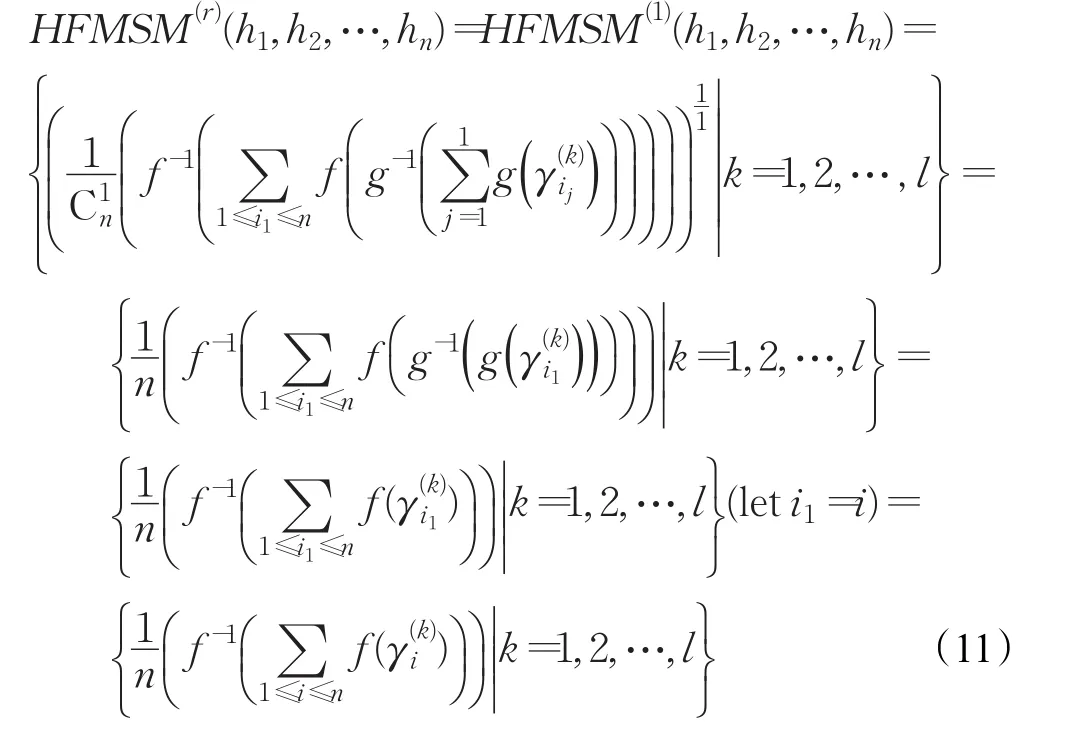
情形2当r=2时，HFMSM()r转化为：

情形3当r=n时，HFMSM()r转化为：

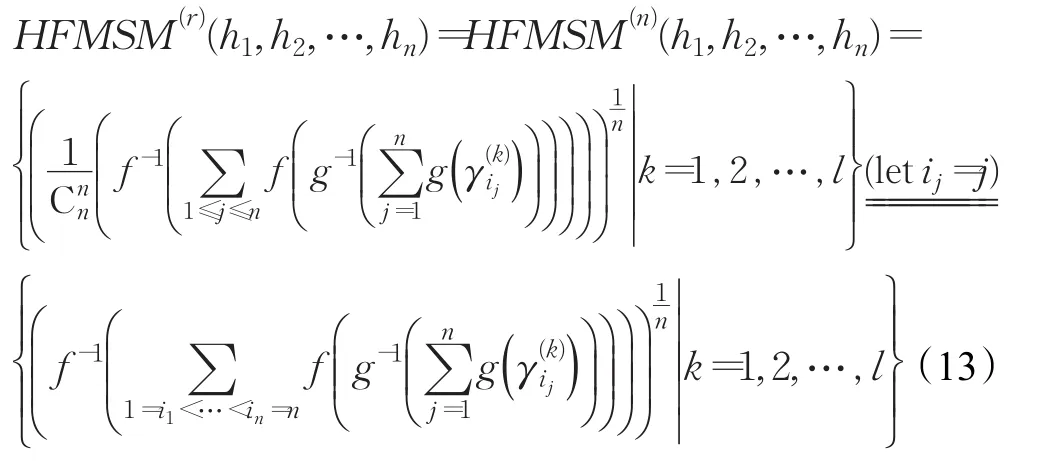
4 基于HFMSM算子的云计算服务商选择决策模型

假设X={X1,X2,…,Xm}为一个给定的备选云计算服务商集合，C={C1,C2,…,Cn}为属性集合。决策层邀请一组相关专家对这些备选云计算服务商在属性集下进行综合评估。在属性值评估过程中，由于每个专家都提供了各自的意见，并坚持保存自己的评估值而不相互谦让，因此为了使得专家们提供的决策信息表达得更为全面和精确，运用犹豫模糊元hij(i=1,2,…,m，j=1,2,…,n)表示这些专家对每个云计算服务商Xi在每种属性Cj下的评估信息，进而构建一个犹豫模糊决策矩阵H=(hij)n×n。接下来，将运用提出的HFMSM算子处理上述多属性群决策问题，具体步骤如下：

步骤1群决策信息标准化。如果所有的属性均为效益型，则不需将决策矩阵H=(hij)n×n进行标准化处理；否则，运用如下方法对原始矩阵进行标准化：

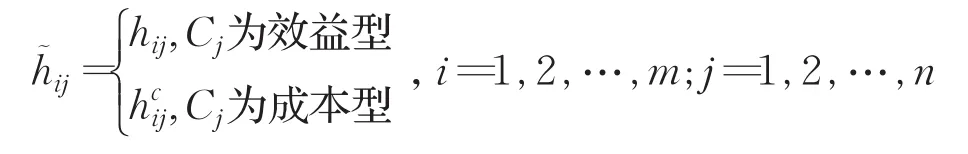
步骤2 基于得到的标准群决策矩阵，运用HFMSM(r)算子：

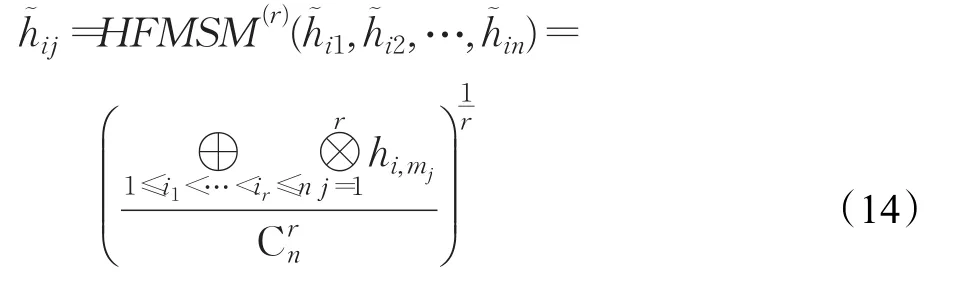
计算每个备选云计算服务商Xi(i=1,2,…,m)的综合属性信息

步骤3计算各备选云计算服务商综合属性信息的得分函数值

步骤4对所有的云计算服务商进行综合性能排序，得分函数越大，则对应的云计算服务商性能越好。

5 算例分析

某金融企业为了完善用户信息材料的存储和保护，保证存储信息时的空间充足，现准备引入一家云计算服务商。根据自身要求和条件，在市场中挑选出了五家合适的服务商X={X1,X2,…,X5}。为了选择出综合条件最优的云计算服务商，该企业邀请了相关领域的专家对这五家云计算服务商在如下四种指标下进行评估，即C1：服务商规模、C2：计算速度、C3：存储质量和C4：售后服务，并且四个指标的重要性相同。评估专家们给出了每家云计算服务商在所有指标下的评估信息hij(i=1,2,…,5，j=1,2,3,4)，从而构建了表1所示的犹豫模糊矩阵H=(hij)5×4。下面利用第4章建立的选择决策模型挑选最合适的云计算服务商。

步骤1由于四种属性指标Cj(j=1,2,3,4)为同一类型指标，即均为效益型指标，因此不需要对原始的矩阵H=(hij)5×4进行标准化。

步骤2运用HFMSM(r)算子对五家服务商在属性指标集下的决策信息进行集成。不失一般性，令r=1，g(t)=-ln t，则计算结果如表2所示。

步骤3计算得到表3中所示的各云计算服务商综合属性信息hi(i=1,2,…,5)的得分函数值。

步骤4依据得分函数值的大小对五家云计算服务商的综合表现进行优劣排序，得分函数值越大，则对应云计算服务商的综合条件最优，具体排序结果见表3。由表3可知，综合条件最合适的云计算服务商为X5。

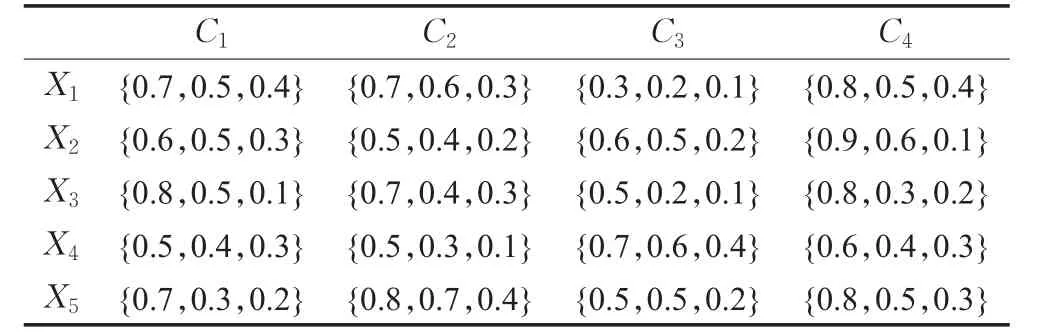
表1 犹豫模糊决策矩阵H=(h ij)5×4

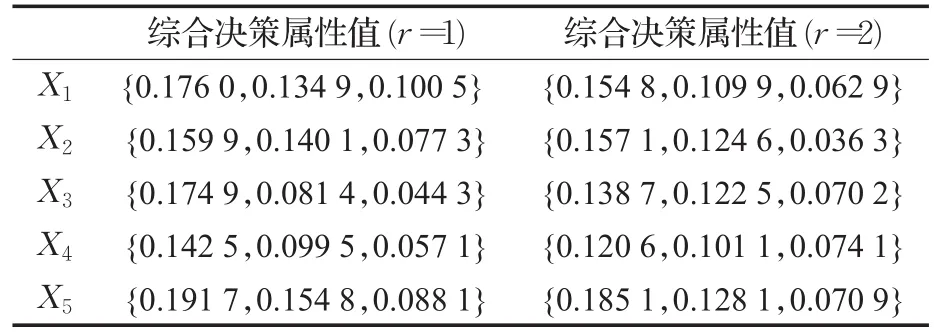
表2 利用HFMSM(r)算子得到各服务商的综合属性值

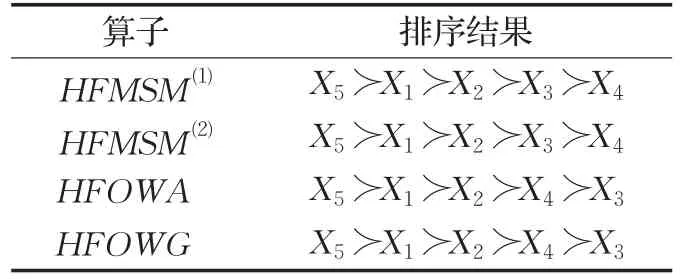
表3 利用不同算子计算得到的排序结果

依据HFMSM(r)信息集成算子的表达形式和3.3节可知，采用不同的参数r，能够得到不同的算子形式，因此下面运用参数r=2进行决策，得到的结果如表2所示，各服务商的排序结果如表3所示。分析发现，虽然运用不同的参数计算得到的五家云计算服务商的综合属性值不相同，但是综合条件最合适的云计算服务商为X5，这说明尽管改变了参数值r，但排序结果仍未变，从而体现了提出的HFMSM(r)算子具有很好的稳定性。另一方面，结合文献[23]中的Maclaurin不等式和定理2，容易得到HFMSM(r)算子是关于参数r的单调递减函数。由表2可以得出，随着r取值的不断增加，HFMSM(r)算子在同一方案下的综合函数值也在减小，这与上述性质相一致。

由于参数r能够反映决策者的主观偏好，可以根据决策者的风险偏好态度来选择r的近似值[24]，在实际问题中一般地取，其中[]表示取整函数，n表示集成的元素个数，同时，参数r取值越大，说明决策者的风险偏好就越高。

下面将与文献[19]提出犹豫模糊决策方法进行对比分析。首先，将犹豫模糊决策矩阵进行标准化。由于属性指标都是效益型属性，因此不需标准化。然后，分别运用文献[19]中的犹豫模糊有序加权平均（HFOWA）算子和犹豫模糊有序加权几何平均（HFOWG）算子：

对各云计算服务商在属性指标下的属性信息进行集成，计算结果如表4所示。

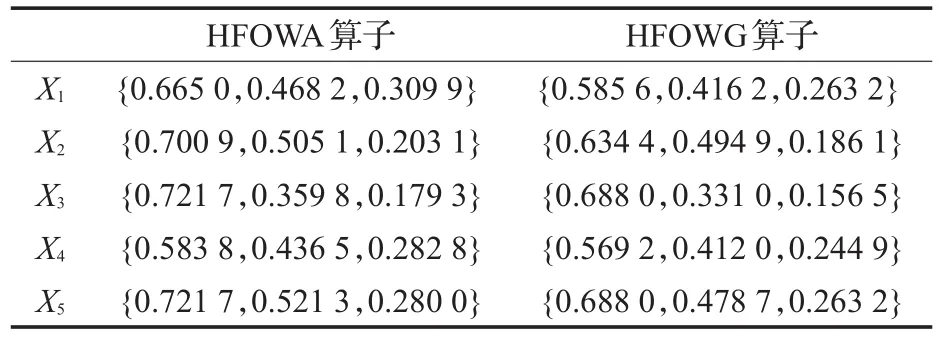
表4 利用HFOWA算子和HFOWG算子得到综合属性值

最后，通过计算综合属性信息值的得分函数对所有云计算服务商进行优劣排序，排序结果见表3。

分析表3中的云计算服务商优劣顺序和综合条件最合适的云计算服务商发现，运用四种算子计算得到的综合条件最合适的云计算服务商相同，即综合条件最合适的云计算服务商都是X5，这说明本文构建的多属性群决策方法具有合理性。然而，五家云计算服务商的优劣顺序存在一定的差异，即运用本文提出的HFMS M(r)算子（参数r=2）得到的云计算服务商X3和X4的优劣顺序与其他方法不相同。事实上，通过原始的犹豫模糊决策矩阵H=(hij)5×4中的决策信息可以发现，云计算服务商X3在四种属性下的属性信息值大体上都高于X4。在四种属性下的属性信息值，这说明云计算服务商X3的综合条件应该优于X4，即X3≻X4，这与运用本文提出的HFMSM(r)算子（参数r=2）得到排序结果相一致，说明了本文提出的HFMSM(r)算子是有效的。另一方面，本文提出的HFMSM(r)算子具有可变参数r，这使得决策更加灵活，能够满足决策者不同的需要，更具有一般性。而文献[19]提出的两个算子不具有可变参数。综上分析可知，本文提出的决策方法是合理的，并且更加灵活可靠。

6 结语

基于Maclaurin对称平均的思想，本文提出了一种基于犹豫模糊Maclaurin对称平均信息集成算子的云计算服务商选择决策方法。首先，在犹豫模糊环境下引入了MSM的思想和Archimedean范数，提出了犹豫模糊Maclaurin对称平均(HFMSM(r))算子，并探讨了其具有的优良性质，即幂等性、置换不变性、单调性和有界性。此外，根据参数值r的变化对该算子的几种特殊情况进行了分析。接着，基于提出的犹豫模糊Maclaurin对称平均算子，构建了一种多属性群决策模型用于云计算服务商的选择决策中，并通过实际问题进行可行性和有效性分析。下一步，主要研究应集中在参数值r的变化对决策结果的影响探讨中，并且建立算法扩展模型，为下一步深入研究奠定基础。