基于改进能量泛函模型的噪声图像分割算法
韩 明,吴朔媚,王敬涛,孟军英
石家庄学院 计算机科学与工程学院,石家庄 050035
1 引言
图像分割技术是计算机视觉领域一项重要的图像分析技术,图像分割技术的优劣直接影响后续的图像处理效果[1]。但是由于噪声、前景与背景对比度低、边界特征模糊、灰度不均匀等现象的出现,使得图像分割变得越来越复杂,因此在图像分割中如何抑制噪声,提高分割精度成为主要研究内容[2]。
为了克服图像灰度不均匀以及噪声对图像分割带来的影响,国内外学者提出了很多解决方案[3-4],在一定程度上实现了对噪声的抑制,在一定程度上解决了灰度不均匀造成的影响,但是有些方法的抗噪性较差。
随着基于动态曲线演化的水平集方法在图像分割中的成功应用,及其在图像分割中的良好性能,基于水平集的图像分割越来越具有独特的优势,它将图像分割的曲线演化问题转化为了偏微分方程的求解,避免了对演化过程中的跟踪。文献[5]提出了局部二值拟合算法(Local Binary Fitting,LBF),该算法利用图像的局部信息进行分割,对于灰度不均匀的图像分割效果较好,但是对于噪声图像,尤其是噪声较强时处理效果较差,并且采用局部信息,容易导致水平集演化过程中陷入局部极小值。一些学者在此基础上提出了全局局部融合图像拟合(LGIF)模型[6-7],融合了图像的局部信息和全局信息,对图像分割的准确度而言具有较大的提升,但是模型对噪声处理能力较差。因此针对噪声图像的分割方法相继提出,例如文献[8]提出局部相似性系数(Region-Based Mode via Local Similarity Factor)模型实现了对椒盐噪声图像分割,但是当噪声较强时分割精度低或者出现了失败的现象。文献[9]提出了结合局部灰度差异的噪声图像分割算法,该算法利用不同噪声条件下像素的灰度差异不同,通过增加噪声修复函数提高图像分割的抗噪性,但是算法复杂度较高,并且容易出现分割的“孤岛”现象。
在图像预处理中存在噪声去除和目标图像边缘保持之间的矛盾,各向异性扩散方程的应用成为解决这一矛盾的合适方法[10]。该方法在图像去除噪声和保持目标边缘细节特征方面具有一定的优势,但是传统的各项异性扩散方程扩散函数在梯度较大的区域容易随着时间的变化而产生明显的“阶梯现象”,为了减少“阶梯现象”的发生,并且在去噪的同时更好地保持图像的边缘信息,本文提出了基于非凸泛函的能量泛函模型实现图像去噪。
在图像去噪的同时为了提高模型的分割速度以及分割精度,本文从能量泛函的最小化入手,对能量泛函模型进行改进提高分割速度以及分割精度。综合考虑图像去噪和分割速度和分割精度等方面的因素,本文提出了基于改进的能量泛函模型的噪声图像分割算法。该算法在图像预处理阶段采用非凸泛函模型构建自适应各向异性扩散方程取代传统的高斯低通滤波去噪,在去噪的同时保持图像中边缘信息的完整性,然后将各向异性扩散方程得到的光滑图像与水平集模型相结合,得到改进的能量泛函模型,通过对新的能量泛函模型求解最小值,得到水平集演化的前景目标的最佳位置。通过对比实验证明本文算法在分割精度和分割速度上具有较高的性能。
2 自适应各项异性扩散方程
2.1 P-M模型
Perona和Malik提出的P-M模型[11]是经典的基于各向异性扩散方程的图像去噪模型,该模型的扩散系数随图像梯度的改变而改变,旨在去除噪声的同时尽可能多地保留边界的细节信息。P-M模型为:

其中,u是随时间变化的光滑图像,div为散度算子,∇为梯度算子,为扩散系数并且为非增函数,与图像梯度成反比。
由两个扩散方程可得:当s→∞时,c(s)→0;当s=0时,c(s)=1,即在梯度较大的地方扩散较小,在图像梯度较小的地方,扩散较大。这些性质使得这两种扩散系数在去除图像噪声的同时一定程度上保护图像边缘特征[12]。但是P-M模型的平滑效果较差,在梯度较大的区域容易随着时间的变化而产生明显的“阶梯现象”,这是由于方程的病态导致在离散问题中的不稳定性。因此在应用过程中为了使得图像的处理结果更加光滑,需要减弱“阶梯现象”的影响。
上述模型的改进均是对偏微分方程的求解,都涉及到对初始水平集的选择与初始化的问题,针对不同的图像需要选择合适的水平集,因此为了避免水平集的初始化,本文直接在离散的灰度水平集上计算能量泛函,而不是求解偏微分方程,从而大大提高分割效率。以下证明不存在全局最小值,通过求解能量泛函的极小值得到对应的欧拉方程。
2.2 改进的能量泛函模型
要得到图像的光滑模型可以将方程(1)看作是一个求能量泛函极小化的能量耗散过程[13],能量泛函的形式如下:


图1 高斯低通滤波与不同灰度水平集进行去噪对比
由于噪声图像的灰度水平集缺乏正则性,而光滑图像的灰度水平集则是正则化的,图1给出了不同图像利用高斯低通滤波进行去噪处理之后的结果,以及采用不同灰度水平集进行去噪之后的对比结果。从左至右依次为高斯低通滤波,灰度值为60,80,100,120和160的水平集去噪结果。由图可以看出经过高斯低通滤波之后的图像,图像边缘变得比较模糊,但是灰度水平集函数处理之后仍旧保留了边缘信息,灰度水平集选择灰度值为100时非常接近图像的边缘。
本文中采用灰度水平集函数杜图像进行处理,当灰度值选择适当时图像的边缘分割准确,并且保持了边缘信息,该方法相较于高斯低通滤波在于能够通过水平集模型使得图像像素灰度与区域均值距离函数相互制约,保持噪声图像的边缘光滑,在曲线演化过程中逼近目标轮廓。
由于图像中的噪声类型不同,因此图像的去噪方法也不尽相同,但是通过对比凸泛函模型与非凸泛函模型在去噪中的特点,发现非凸泛函模型能够更好地保持图像的边界信息[14]。
因此本文提出了基于非凸泛函的能量泛函模型实现图像的去噪处理。模型如下:

为了保证模型为非凸泛函,因此0<α<1,从而保证目标边缘信息被保留,f为噪声图像,λ>0为调整参数,起到平衡平滑和保真的作用。
以下证明式(3)不存在全局最小值。
假设E(u)存在全局最小值点,则有E(u)=0,可得:

由式(4)可见,如果式(4)成立,则需要满足 u=f和u′=0,而这两者在图像空间Ω上几乎处处都成立,但是又由于 f不可能为常值函数,因此在E()u的解空间中不存在全局最小值。
通过求解式(3)能量泛函模型的极小值,即欧拉方程可得:


在图像u的等灰度线的切线方向T=(-uy,ux)和法线方向N=(ux,uy)上的扩散,分别用uT和uN标记如下:

由式(5)可得,当0<α<1时,在图像u的法方向的扩散系数为:

由式(8)可得对于式(5)的扩散模型而言总是在法方向N=(ux,uy)上发生倒向扩散,从而更好地保护图像中目标边缘信息。
图像的边缘信息是区分图像不同区域的最直观的准则,作为图像分割的最重要特征信息,由于非凸泛函可以减小Heaviside函数在目标轮廓处的模糊程度,一方面非凸函数使得正则项可以近似表示为的加权l0范数,从而使得Hε(ϕ)的支撑更加靠近Heaviside函数的支撑,另一方面采用非凸泛函使得水平集演化的停止函数在光滑区域更加接近于1,在图像的边缘区域更加接近于0,因此通过非凸泛函模型使得演化过程中更好地保持图像的边界信息。
通过上述证明过程,通过基于非凸泛函的能量泛函模型获得的扩散模型能够得到光滑的图像边界,并且保持了图像中目标边缘信息的完整性。
3 CV模型能量泛函实现图像分割
3.1 CV模型表示与分析
C-V水平集模型[15-16]是基于图像区域信息的集合活动轮廓模型,通过最小化能量泛函的方式来演化曲线,设图像I(x,y)被闭合曲线C划分为目标和背景两个同质区域,两个同质区域的平均灰度值分别为Co和Cb,图像的拟合能量泛函定义如公式(9)所示:

式中,μ,ν≥0,λ>0为各个能量项的权重系数,均为常数。L(C)为闭合曲线的长度,A(C)为曲线C的内部区域的面积。 δ(ϕ)是一维的Dirac函数,H(ϕ)表示Heaviside函数,ϕ(x,y,t)为水平集函数。当闭合曲线C达到两个区域的边界时,Ecv(C,Co,Cb)取得最小值,由于CV水平集模型是水平集思想与Mumford-Shah模型的结合,即C-V水平集模型是Mumford-Shah模型的特例,又因为Mumford-Shah模型的泛函存在极小值,所以C-V水平集模型的能量泛函Ecv(C,Co,Cb)一定存在极小值。即最优化式(9)可得最终的目标图像的分割曲线C的位置。
CV模型的示意图如图2所示,图2(a)表示演化曲线包含目标轮廓图;图2(b)表示目标轮廓曲线包含演化曲线;图2(c)表示目标轮廓曲线与演化曲线相交;图2(d)表示演化曲线与轮廓曲线相重合,只有在图2(d)所示的情况下能量泛函Ecv(C,Co,Cb)取极小值。

图2 CV模型示意图
为了计算式(9)中的数值解进行能量泛函的逼近计算,Dirac函数δ(x)采用正则化函数δε(x),其定义如下:

在实际应用中利用数值计算的方法计算H(x)函数比较困难,因此在本文中选择非紧支撑、光滑并严格单调的正则化形式:

与本文的式(11)进行对比实验的是式(12)的CV模型中的Heaviside函数:

对比实验结果如图3所示。

图3 Hε(x)函数对比
实验中ε的取值均为0.1。由图可见当ε的取值相等时,本文的非紧支撑、光滑并严格单调的正则化Hε(x)函数相对于式(12)中传统CV模型中选择的Hε(x)函数而言能够更好地逼近Heaviside函数,因此可见本文的正则化函数对在分割精度上更高。
Dirac函数的正则化函数δε(x)和Heaviside函数的正则化函数Hε(x)对于不同的ε取值如图4所示。

图4 不同ε值的δε(x)函数
由图4可见如果ε取值太小(如:ε=0.5)则δε(x)的值趋向于0,由图可见其作用范围很窄,从而导致能量函数陷入局部极小化,如果初始轮廓距离目标较远,容易出现目标分割失败的现象。如果ε取值太大(如:ε=2),由图可见虽然δε(x)可以得到全局最小化,最终目标轮廓可能会不精确[17]。
即当 ε→0 时,δε(ϕ)→δ(ϕ),Hε(ϕ)→H(ϕ),此时能量泛函Ecv(C,Co,Cb)的逼近形式为:

通过求解能量泛函对应的Euler-Lagrange方程实现对式(13)的极小化,利用有限差分法得到如下的水平集演化方程,将ϕ表示为梯度流下降的形式为:


通过上述演化方程可得到水平集函数ϕ(x ,y,t)的演化过程,同时可得演化曲线的演化过程,因此经过若干次迭代演化之后初始图像通过演化曲线被分割,即如图2(d)所示的分为了曲线内部的部分和曲线外部的Ωb=部分。
3.2 模型的灰度水平集算法实现
利用第2章中提出的各项异性扩散模型得到的光滑图像u对式(13)的能量泛函进行改进得到新的模型,并且求解能量泛函的最小值,得到水平集演化的前景目标的最佳位置。
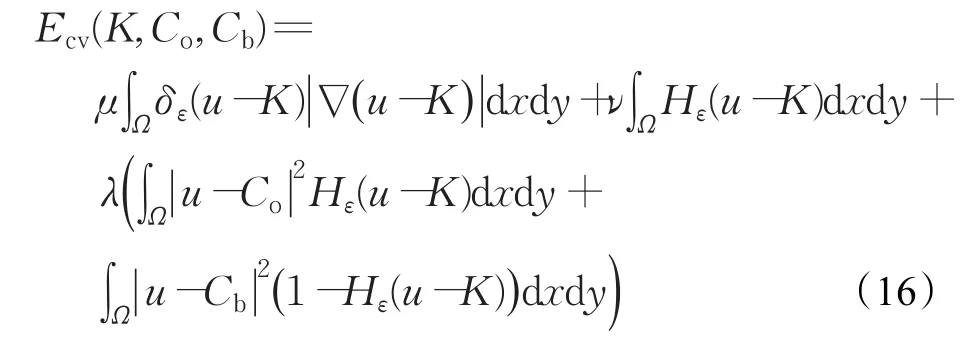
其中:


由式(17)和式(18)可见改进之后的新模型是只依赖于K的函数。
根据变分法和Euler-Lagrange方程,求解式(18)对Euler-Lagrange方程表示的水平集演化方程为:

求解式(18)对应的能量泛函最小值问题即演化为求解式(19)中目标零边界条件的Euler-Lagrange方程的解:
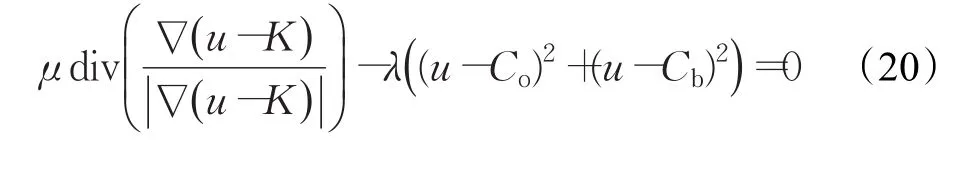



即

则有,如果L(C)为非常值函数,由式(24)可见,存在极小值点K∈(Kmin,Kmax)使得 E′cv(K)=0。
本文的改进能量泛函模型主要做了以下几方面的改进:
(1)采用基于非凸泛函的能量泛函模型实现图像的去噪处理,在图像去噪的同时,利用非凸泛函的图像边缘保持特性,保持图像的边缘信息,使得水平集演化时更加准确。
(2)利用式(11)的正则化函数代替式(12)的正则化函数使得目标函数更好地逼近Heaviside函数,从而提高图像分割的准确性。
(3)利用通过各项异性扩散模型得到的光滑图像u代替水平集函数ϕ,实现对噪声图像的非同质区域的边缘抑制外,能够更好地进行全局优化。
(4)在算法的时间复杂度上本文算法主要在于通过各项异性扩散模型得到的光滑图像u与水平集函数ϕ之间的差异,本文算法在能量泛函的迭代求解过程中由于采用了各项异性扩散方程实现光滑图像的获取,在每一步的迭代中每个时间步长总是保持减小,直到这种状态保持到模型达到稳定为止,而传统的方法中时间步长保持不变,因此相对而言本文算法的运算复杂度相对较小,通过第4章实验中的运行时间的计算同时证明了本文算法运算的复杂度较小。
3.3 本文算法具体步骤
在上述论述的基础上,本文基于各向异性扩散的灰度水平集图像分割算法步骤如下:
步骤1输入原始图像I(x,y)利用式(3)的非凸泛函能量泛函模型实现图像的去噪处理,得到去噪之后的光滑图像u。
步骤2对步骤1中得到的光滑图像u给出初始化曲线C,初始参数设置如下:
离散网格的间隔为h=1,时间步长为Δt=0.1,正则化参数ε=1,输入的原始图像u中的待分割目标较小,长度惩罚项L(C)的权值μ取较小的值,当待分割目标较大时则 μ取较大的值,其取值形式可表示为μ=O×2552,其中O∈[ ]0,1。
步骤3根据式(19)的水平集函数的演化方程,求出演化的水平集函数u-K。
步骤4根据步骤3中的水平集函数u-K ,提取出零水平集。
步骤5求解式(18)对应的能量泛函最小值,判断演化是否停止,如果停止,则为水平集演化的目标最佳边缘位置,给出分割结果,算法结束,否则,转到步骤3继续。
4 实验分析
为了验证本文算法的有效性,本文选取了不同的视频图像序列进行去噪和分割实验,与本文进行对比实验的算法是考虑局部图像信息的LBF算法和文献[9]的结合局部灰度差异的噪声图像分割算法。
4.1 实验环境和参数设置
本文的实验环境如下:实验采用Matlab R2009a作为仿真环境,实验计算机配置为:Win10操作系统,Intel Core i7-6700 CPU 3.40 GHz,64 GB内存。无特别说明,实验中参数设置如下:离散网格的间隔为h=1,时间步长为Δt=0.1,正则化参数ε=1,λ=1.0,标准方差随处理图像的不同而不同。对算法性能的定量评价,采用迭代次数和运行时间评价算法的计算效率,采用True Positive Rate(TPR),False Positive Rate(FPR)和Similarity Index(SI)[18]进行分割精度的度量。
4.2 实验处理与分析
4.2.1 算法噪声处理能力实验
首先测试本文算法对噪声的处理能力。如图5所示为三幅具有高强度噪声的图像,运用本文算法进行噪声处理和分割,由图4可见本文算法在高强度噪声下的目标分割取得了较好的效果。

图5 高强度噪声下本文算法的分割结果
4.2.2 不同算法对比实验
为了实现对算法性能的定量评价,本文采用真阳性比率(True Positive Rate,TPR),假阳性比率(False Positive Rate,FPR),相似性系数(Similarity Index,SI)三个度量进行评估。三个度量的定义如下:

其中,ST表示图像中待分割图像的真实前景区域像素集,SA表示通过模型分割算法所获取的前景区域像素集,理想情况下,SI和TPR接近于1,FNR接近于0,表示算法性能越好,TPR值越大,FN R越小说明更多的真实目标区域被分割区域所覆盖,SI值越大说明目标区域与分割区域相似度越高。
另外对于本文算法的分割精确性的度量,通过测量分割之后的目标轮廓与真实目标轮廓之间的距离进行比较,即均方根误差(Root Mean Square Error,RMSE)进行比较[19]。

(1)增加不同噪声的算法比较
如图6所示为在本文算法和文献[9]算法对原始图像上增加了不同程度的噪声之后的图像的分割结果,其中后两幅图像分别增加了标准差为0.01和0.02的高斯噪声。在实验中两个算法的μ=0.06×2552。

图6 不同噪声的图像分割结果
由图可以看出对于原始图像和噪声污染程度较低的图像本文算法和文献[9]算法均能够实现正确的图像分割,并且SI和TPR的值都接近于1,FPR接近于0,但是对于增加标准差为0.02的噪声时,由图可以看出当噪声增强时分割结果的准确性不同,本文算法比文献[9]算法的分割结果更加精确。此时文献[9]算法和本文算法SI分别为0.935和0.991,TPR分别为0.982和0.995,FPR分别为0.008和0,通过定性分析可见本文算法抗噪性更强。
图中标准差0.01和0.02情况下的均方根误差比较如表1所示。

表1 不同噪声图像分割的均方根误差比较
(2)边缘模糊图像对比实验
该实验采用肿瘤图像作为分割图像,旨在比较不同的算法对前景目标灰度和背景相似的图像的分割结果的比较,在实验中μ=0.02×2552。该图像噪声强,目标图像的边缘特征模糊,由图7可见,LBF算法能够有效地进行分割,但是对于第三列的背景与前景目标边界不明显的图像来说分割失败,对于文献[9]算法而言由分割结果可见能够准确地定位目标的边界,但是出现了部分“孤岛”现象,本文算法对于所实验的图像均能够达到较好的分割效果。由表2可以看出本文的算法分割精度相对较高,算法分割性能较好,在相同的迭代次数下用时较短。
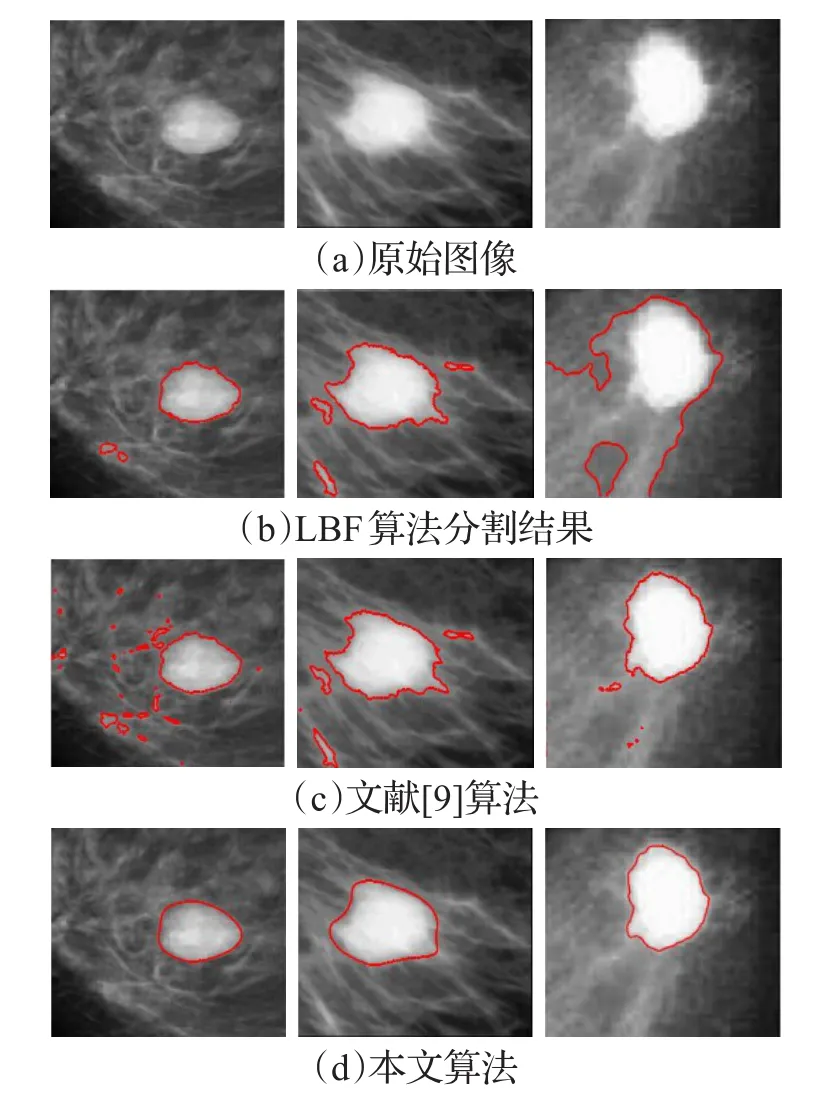
图7 不同算法对肿瘤图像分割结果
(3)MR图像分割实验
该实验采用真实的医学超声图像进行分割实验,实验目的是分割出图像中的白质边界,三幅均带有较大程度噪声的医学超声图像,并且边界模糊,在实验中μ=0.02×2552。由图可见在噪声干扰下,LBF算法和文献[9]算法均没有能够成功地提取出白质轮廓,文献[9]算法效果比LBF算法效果较好,但是仍然存在一些不正确的边界定位,而本文模型则能够准确地演化到白质边界,效果较好。三个图像分割的均方差误差和重叠区域误差比较如表3所示,由表数据可见,在图像中LBF算法效果较差,重叠区域误差较大,运行时间相对较长,本文算法相对于其他两种算法对于噪声图像具有更好的分割性能。

表2 图7中三幅图像分割结果的均方误差、重叠区域误差、运行时间比较

图8 不同算法对MR图像分割结果

表3 图像分割结果的均方误差、重叠区域误差、运行时间比较
5 结束语
为了提高水平集对图像分割的抗噪性,本文在分析了各向异性扩散方程和CV水平集模型的基础上,提出了一种基于各项异性扩散方程和灰度水平集的噪声图像分割算法。与LBF和文献[9]中的模型相比,本文的算法在强噪声环境下具有更好的鲁棒性,并且能够实现对强噪声图像的高精度分割。本文模型通过引入非凸泛函到能量泛函模型,实现对噪声图像平滑处理的同时保持前景目标边缘信息。然后将平滑之后的图像函数与水平集能量泛函模型相结合实现对强噪声图像中目标边界的水平集准确演化,从而保证在强噪声环境下图像分割的准确性。最后本文通过多组对比实验进行分析和验证,证明了本文提出的算法对噪声图像的分割具有优越性。

