基于梯度下降的脉冲神经元精确序列学习算法

杨 静，赵 欣，徐 彦，姜 赢

1.北京师范大学珠海分校 管理学院，广东 珠海 519087

2.南京农业大学 信息科技学院，南京 210095

1 引言

脉冲神经元的输入输出均为一串离散的脉冲激发时间，通过脉冲序列表示并处理信息。脉冲神经网络以脉冲神经元为基本构成单元，相比传统的人工神经网络有着更强大的计算能力。因此，脉冲神经网络已有越来越多的研究者从不同方面对其进行研究[1]。由于基于脉冲激发时间的编码方式能够在一个相对短的时间内携带更多的复杂信息[2]，研究者希望能通过样本学习使得脉冲神经元能够在精确的时间点上激发出脉冲而不是仅仅学习激发出特定激发率的脉冲序列。

在生物学研究中有大量的证据表明：在大脑皮层中的确存在着有监督学习的行为[3]，因此有监督学习算法在脉冲神经网络中也被广泛应用。现有的脉冲神经网络有监督学习算法大致可以分为三大类：基于梯度下降的、基于突触可塑性的以及基于脉冲序列卷积的学习算法[4]。例如，Bohte等人最早提出了一种单脉冲神经网络的反向传播算法：SpikeProp[5]，该方法通过近似的将脉冲激发时刻附近的神经元内部状态看作线性函数的方法将BP算法推广到脉冲神经网络中。在此基础上还出现了各种推广算法，例如：带动量的反向传播，QuickProp，Rprop，Levenberg-Marquardt BP以及基于隐层多脉冲的反向传播学习算法[6-9]。Xu等人提出了一种基于梯度下降的多层前馈脉冲神经网络多脉冲输出的有监督学习方法（MSGDB），该方法中各层神经元的输出均可以为多脉冲[10-12]。Florian提出了一种名为Chronotron[13]的方法，其中包括了两种学习机制：E-learning和I-learning。E-learning学习机制同样基于梯度下降，不同的是该方法采用VP距离来度量实际输出与目标输出脉冲之间的差异。最近Lin等人提出了另一种基于反向传播的脉冲神经网络的学习算法，其中误差函数是基于输出脉冲序列的内积而构建，算法同样可以推广至多脉冲激发的多层脉冲神经网络[14]，也有研究者提出了一种基于反向传播的脉冲神经元深度学习算法[15]。

突触可塑性的有监督学习方法主要基于生物神经元的突触调整机制，例如STDP（Spike-Timing-Dependent-Plasticity）规则[16]。ReSuMe方法[17]是一种基于 Widrow-Hoff规则并结合STDP规则的脉冲神经元有监督学习方法，具有较好的学习性能和适用性，但该方法只适合于单层网络的学习。Sporea[18]等人提出一种结合BP算法的Multi-ReSuMe方法，以解决多脉冲激发的多层网络学习问题。文献[19]中提出了一种基于ReSuMe方法的输入脉冲选择改进学习算法以提高学习的精度。Wade等人结合STDP规则与BCM（Bienenstock-Cooper-Munro）学习规则给出了一种名为SWAT[20]（Synaptic Weight Association Training）的多层前馈脉冲神经网络的学习算法。Chronotron中的I-learning学习机制[12]也是依据STDP规则调整权值，不同的是该方法以在线方式运行，更加符合生物神经元的行为特性。

基于脉冲序列卷积的有监督学习算法通过选择合适的核函数将脉冲序列转换成一个连续函数以进行进一步的定量分析。例如SPAN（Spike Pattern Association Neuron）算法[2]采用卷积方式将离散的脉冲激发时间转换为所对应的实数值并将其代入Widrow-Hoff规则得到权值调整公式。类似的方法PSD（Precise-Spike-Driven）[21]基于LIF神经元模型提出，但该方法只对输入脉冲进行卷积。Lin等人[22]提出了一种基于nSTK（nonlinear Spike Train Kernels）的在线有监督学习算法，该算法利用Laplacian核函数与一个非线性函数一起完成对输入脉冲序列的转换。另一种基于脉冲序列卷积学习方法FILT（FILTered-error）[23]利用一个滤镜函数处理目标与实际输出脉冲之间的误差后再通过调整权值逐步降低这个误差值，该方法是基于随机的学习模型提出的。

基于梯度下降的多脉冲神经元学习算法中的MSGDB方法具有较高的学习精度[24]，但该方法采用一种动态误差函数来计算权值调整值，在神经元的序列学习中有可能会遇到实际输出脉冲个数和目标脉冲个数不等但算法已经收敛并结束的情况。基于MSGDB方法的这一固有缺陷，本文提出了一种基于梯度下降的脉冲神经元精确序列学习算法。该算法通过引入虚拟激发脉冲，使得算法能在提前结束时利用虚拟激发脉冲继续进行学习，并最终使得神经元能够精确激发出和目标序列个数一致的脉冲序列。

2 SRM神经元模型简介及相关算法介绍

2.1 SRM神经元模型

脉冲神经元的种类较多，例如：SRM模型（Spike Response Model），LIF模型（Leaky Integrate-and-Fire Model）和HH模型（Hodgkin-Huxley model）等[25]。其中SRM模型具有显式的膜电位表达式，可以方便地对表达式进行求导计算，进而研究神经元的运行方式以及学习算法。同时LIF模型和HH模型都可以通过求解微分方程等方法将其转换成类似SRM模型的形式，本文选用SRM神经元模型作为研究对象。

在SRM模型中，神经元接收由多个突触传输过来的一串离散的脉冲时间序列。所有的脉冲在到达神经元后就会产生突触后电位（Postsynaptic Potential，PSP），并和突触的权值一起作用使得神经元的内部状态即膜电位值（membrane potential）发生变化，其计算公式如下所示：

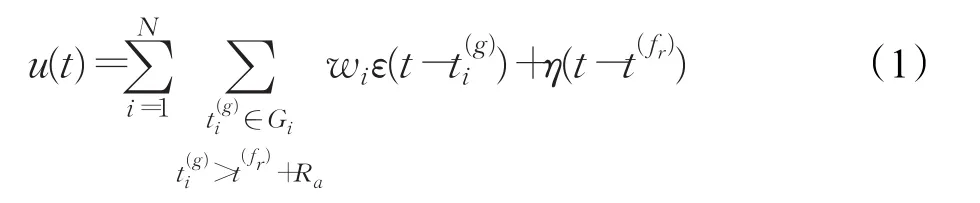
其中，N为神经元输入突触的个数；wi为神经元的第i个输入突触的权值；为第i个突触的第g个脉冲到达神经元的时间；Gi为第i个突触的输入脉冲集合；为当前时刻t(t＞0)之前最近的一次脉冲激发时刻；Ra为绝对不应期长度。从上式中可以看出，当时，也就是如果脉冲到达时间小于等于最近一次脉冲激发时刻与绝对不应期长度之和时，该脉冲在膜电位的计算中是无效的。Ra直接决定了神经元在激发后的一个短时期内不会再次激发脉冲，这个时期被称为绝对不应期。ε()为反应函数，它决定一个输入脉冲产生的PSP大小，其表达式如下所示：

其中τ是决定反应函数形态的时间延迟常数。

当神经元的膜电位值不断增加直到超过神经元的激发阈值ϑ时，神经元就会在该时刻激发出一个脉冲，并且膜电位值立即降为0。随后神经元会进入一个相对不容易再次激发脉冲的时期，这个时期称为相对不应期。相对不应期由膜电位计算公式（1）中的η(t)函数描述：

其中τR是决定不应期函数形态的延迟常数。显然这是一个恒负函数，t越小也就是当前时刻和最近激发时刻越接近时，η(t)值越小，从而导致膜电位值越小，越不容易超过阈值。当神经元还没有脉冲激发时，η(t)恒等于0。

2.2 MSGDB算法及其缺陷

MSGDB算法根据神经元实际输出序列和目标序列构建误差函数，通过计算梯度调整权值并最小化该误差函数。由于脉冲神经元的输出是一串脉冲序列，在学习过程中可能出现神经元的实际脉冲输出个数和目标脉冲输出个数不相等的情况。MSGDB的解决方案则是采用动态选取脉冲的方法，即选取相对应的实际输出脉冲和目标输出脉冲进行误差计算。MSGDB算法有两种运行方式：在线和离线学习方式。离线学习方式在神经元每一轮运行结束后根据实际输出脉冲序列和目标输出脉冲序列构建误差函数，并进行权值调整。而在线学习方式当神经元一旦有实际脉冲激发时就立刻和相对应的目标脉冲构建误差函数以调整权值。这种学习方式更符合生物学基础，大量实验也证明在线学习方式有着更高的学习精度。因此本文也以在线学习方式为研究对象开展讨论。

当实际激发序列和目标激发序列脉冲个数不相等时，就会有实际激发脉冲或者目标激发脉冲没有相对应的激发脉冲来构建误差函数。如果此刻之前的误差函数并未完全等于零，学习将继续调整权值。然而当误差函数完全等于零时即前若干个输出脉冲已经完全学会时，就会由于没有可计算的误差函数而导致神经元在未完全学会的情况下提前停止学习。提前停止分为两种情况。情况1：神经元仅仅学会了目标序列中的前若干个脉冲而未能激发出最后的若干个脉冲；情况2：神经元学会了全部目标序列但在目标序列最后一个激发脉冲之后还激发了若干个多余的脉冲。在以上两种情况下，误差函数均为0，算法认为学习已经收敛而停止学习。图1为这两种情况的具体示意图。

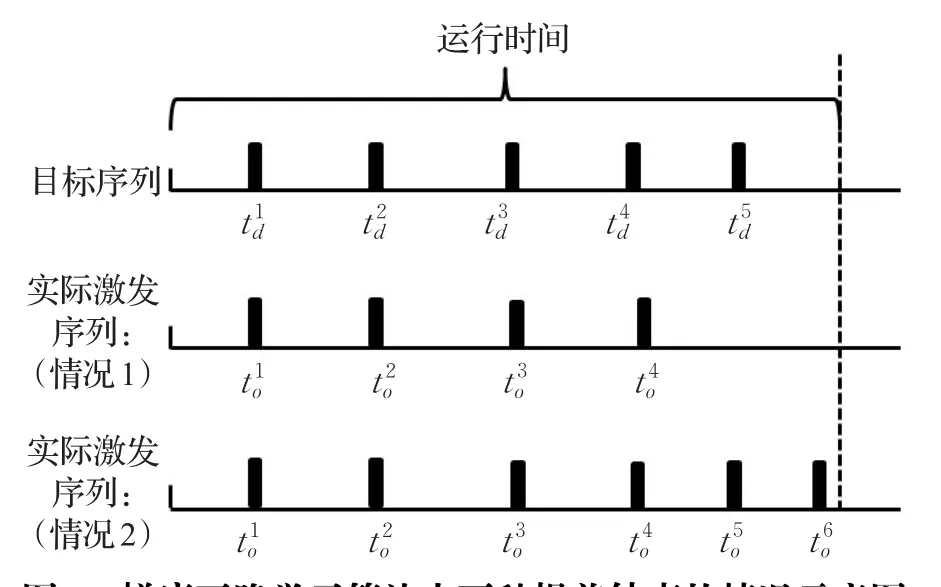
图1 梯度下降学习算法中两种提前结束的情况示意图

3 精确脉冲序列学习算法

基于2.2节中所讨论的多脉冲神经元梯度下降学习算法可能收敛于个数不等的脉冲序列的缺陷，本文给出了一种基于虚拟脉冲的改进算法。以下分别以实际输出脉冲个数不足以及实际输出脉冲个数多余两种情况为例具体介绍该算法。

3.1 实际输出脉冲序列个数不足情况

如图2所示，神经元的运行时间为Tt；接收突触传递过来的若干输入脉冲；目标输出序列为；实际输出序列为。显然神经元已完全学会了目标输出序列中的前F个脉冲，但却未能激发出目标输出序列中的最后M个脉冲如果将神经元的运行看作是一个连续过程，并且在Tt时刻之后继续接收后续输入脉冲等，那么随着输入脉冲对于神经元膜电位的不断积累增加作用，可以预见神经元将在Tt之后的某时刻继续激发出脉冲（如图2所示）。那么让神经元继续激发出额外的脉冲就可以看作是使得未来的输出脉冲提前激发至运行时间之前。然而由于的具体激发时间无法得到，采用虚拟实际激发脉冲来与目标序列中被遗漏的最后M个脉冲配对来构建近似的误差函数。应该大于运行时间Tt以保证权值调整方向的正确，并且取值越大意味着调整幅度越大。

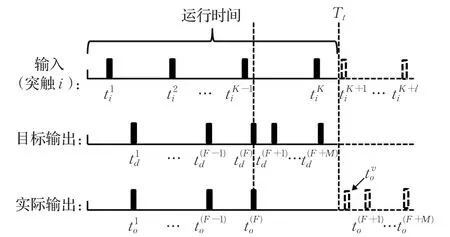
图2 实际激发个数不足情况下虚拟脉冲示意图

由于神经元已经完全学会了前F个输出脉冲，那么前F个误差函数均等于零。为了使得神经元继续激发，新的误差函数由目标输出序列中的最后M个脉冲分别与M 个虚拟实际激发脉冲构建：

权值的更新值Δwi为：

类似于MSGDB算法：

B部分的计算方法和多脉冲神经元梯度下降学习算法类似：

3.2 实际输出脉冲序列个数多余情况

类似的，实际输出多余情况如图3所示，神经元已完全学会了全部的目标输出序列，但却多激发出了最后M个脉冲。那么让神经元不激发出这些额外的脉冲就可以看作是使得这些多余的输出脉冲延后激发至运行时间之后。同样可以假设目标输出序列在运行时间Tt之后还有额外的期望输出脉冲，并采用一个虚拟目标激发脉冲来近似代替与实际输出序列中多余的最后M个脉冲配对来构建一个近似的误差函数。同样需要大于运行时间Tt以保证权值调整方向的正确，并且取值越大意味着调整幅度越大。

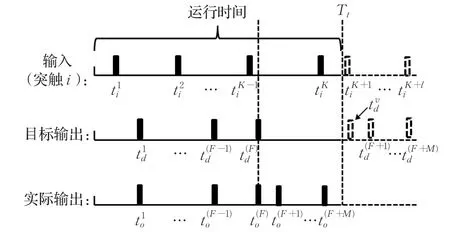
图3 实际激发个数多余情况下虚拟脉冲示意图

类似的，在这种情况下为了使得神经元继续激发，新的误差函数构建如下：

同样，Δwi的计算如下所示：

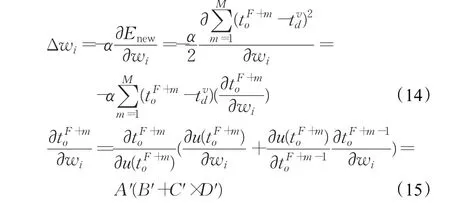
类似的，有：

D′部分的计算方法与上一节类似。

3.3 精确脉冲序列学习算法讨论

以上分别介绍了两种输出脉冲个数不等情况下利用虚拟激发脉冲构建误差函数和调整权值的方法。在该方法的实际应用中还有一点需要仔细讨论，即究竟在什么时候采用虚拟激发脉冲构建新的误差函数。2.2节中提到的原始的MSGDB算法本身是有一定的脉冲个数收敛能力的。在算法运行过程中可能出现输出脉冲个数不等的情况，而算法也有可能将其纠正过来。由于神经元在学习结束前并不知道学习是否会收敛于个数不等的脉冲序列，那么精确脉冲序列学习算法有两种运行方式：（1）只有当算法已经收敛且输出脉冲个数不等时才采用虚拟激发脉冲进行纠正；（2）在每轮学习结束后一旦遇到输出脉冲个数不等的情况就采用虚拟激发脉冲进行纠正。这两种算法分别缩写为V1-MSGDB和V2-MSGDB。对于V1-MSGDB而言，在算法第一次收敛之前的学习轨迹和MSGDB是完全一致的。而对于V2-MSGDB而言，只要在运行过程中出现输出个数不等的情况，那么算法将增加虚拟脉冲来构建误差函数，这将导致学习轨迹和MSGDB完全不一样。两种算法的学习效率是有差异的，流程分别如下所示：

V1-MSGDB算法流程

输入：输入脉冲序列，目标序列，初始权值以及学习速率

（1）利用MSGDB训练神经元

（2）如果C=1且目标序列中脉冲个数大于实际输出序列中脉冲个数

（2.1）利用公式（5）构建误差函数

（2.2）利用公式（6）～（12）计算 Δwi并更新权值（2.3）转到（1）

（3）如果C=1且目标序列中脉冲个数小于实际输出序列中脉冲个数

（3.1）利用公式（13）构建误差函数

（3.2）利用公式（14）～（19）计算 Δwi并更新权值

（3.3）转到（1）

输出：权值

V2-MSGDB算法流程

输入：输入脉冲序列，目标序列，初始权值以及学习速率

（1）利用MSGDB训练神经元

（1.1）如果一轮学习结束后目标序列中脉冲个数大于实际输出序列中脉冲个数

（1.1.1）利用公式（5）构建新误差函数

（1.1.2）利用公式（6）～（12）计算 Δwi并更新权值

（1.1.3）继续下一轮学习

（1.2）如果一轮学习结束后目标序列中脉冲个数小于实际输出序列中脉冲个数

（1.2.1）利用公式（13）构建新误差函数

（1.2.2）利用公式（14）～（19）计算Δwi并更新权值

（1.2.3）继续下一轮学习

输出：权值

另一个需要说明的问题是：虚拟脉冲激发时间的取值。在算法中需要利用虚拟脉冲来和实际激发时间或目标激发时间配对构建误差函数，一个合适的虚拟脉冲应该能尽快地使得神经元激发出额外脉冲或者消除多余脉冲，但同时又使得权值调整对原学习结果的破坏最小。而这个合适的取值和神经元的突触权值大小，输出脉冲时间以及目标脉冲序列等参数紧密相关。类似于学习速率的取值，目前并无一个明确的取值方案。从最小调整的原则出发和可以取值为Tt+1。因为虚拟脉冲的取值直接和权值的调整幅度相关，取值越大，调整幅度越大。为了避免权值调整过大对原有学习结果的破坏，可以采用最小值。而Tt+1只是保证调整方向正确的最小的虚拟激发时间并不能保证一定获得最好的学习效果。在下一章的实验中，将通过设置不同取值的虚拟脉冲对其进行进一步的结果分析。总之，本文提出的基于梯度下降的精确序列学习算法在原有MSGDB算法的基础上，引入虚拟脉冲构建误差函数来对神经元的输出脉冲个数进行调整。其中虚拟实际脉冲可以使得神经元增加脉冲激发个数而虚拟目标脉冲的引入可以使得神经元减少激发个数。算法通过比对实际输出脉冲个数和目标输出脉冲个数采取新的误差函数引导学习朝着正确激发个数的方向进行，并最终达到精确学习的目标。

4 算法实验验证

本章通过一系列对比实验来验证所提出的精确脉冲序列学习算法的效果。实验中的神经元的输入脉冲序列和目标输出脉冲序列均为给定激发频率的Poisson序列，Fin代表输入激发频率，Fout代表输出激发频率。其他一些神经元的参数如下所列：τ=7 ms，τR=80 ms，ϑ=1，Ra=1 ms。神经元的初始权值是在给定区间内取的均匀分布的随机值，学习速率设为0.003，每次学习的最大步数设为1 000步。

在第一个实验中，选取的神经元有200个输入突触，在200 ms的运行时间内接收Fin=5 Hz的输入脉冲，其学习目标脉冲序列为Fout=80 Hz的Poisson序列，初始权值的产生区间为：[0，0.25]。首先取进行实验，图4、图5分别显示了V1-MSGDB的学习结果。

图4 V1-MSGDB学习精度变化示意图（激发个数不足）

图5 V1-MSGDB从53步到225步学习过程示意图（激发个数不足）

从图4中可以看出算法在53步时第一次达到精度1，但此刻神经元的输出少激发了最后两个目标脉冲。MSGDB算法将在53步时停止学习而V1-MSGDB算法在检测到输出个数不等后利用虚拟脉冲继续调整权值，又通过172步学习使得神经元精确激发出目标脉冲序列。在图4中可以看到在第54步时精度有一个急剧下降，这是由于虚拟脉冲带来的精度损失，但之后可以看到精度随着学习步数的增加逐渐增大，最终达到1，并激发出了全部目标脉冲。

图6、7分别显示了另一种算法V2-MSGDB的学习结果。

图6 V2-MSGDB学习精度变化示意图（激发个数不足）

图7 V2-MSGDB学习过程示意图（激发个数不足）

可以看出V2-MSGDB只有1次也就是最后一步收敛于精度1，并且激发出了全部的目标脉冲。相比V1-MSGDB的225步的收敛步数，整个学习过程只花了117步。因为该算法在每一轮学习结束时一旦遇到激发个数不等立即使用虚拟脉冲来调整权值，能有效避免算法收敛但激发个数不同的情况出现。在本例中，第一轮学习结束后精度为0.134 5，神经元输出为脉冲12个，与目标脉冲个数相等；第二轮学习结束后精度为0.173 5，神经元输出脉冲为19个，比目标脉冲个数多了7个。在第三轮学习中，V2-MSGDB检测到输出个数不足立刻引入了虚拟目标脉冲来构建误差函数使得这一轮学习结束后神经元激发个数降到10个，而V1-MSGDB仍然采用原有的误差函数调整，并使得调整结束后神经元激发个数变为13个。因此从这一轮开始两种算法的学习轨迹完全不同。

表1 不同取值虚拟脉冲的收敛步数（实验一）

第二个实验中，利用和实验一相同的神经元参数设置，不同的是选取了一个神经元有多余激发例子来进行实验。图8、9为V1-MSGDB的学习过程示意图。

图8 V1-MSGDB学习精度变化示意图（激发个数多余）

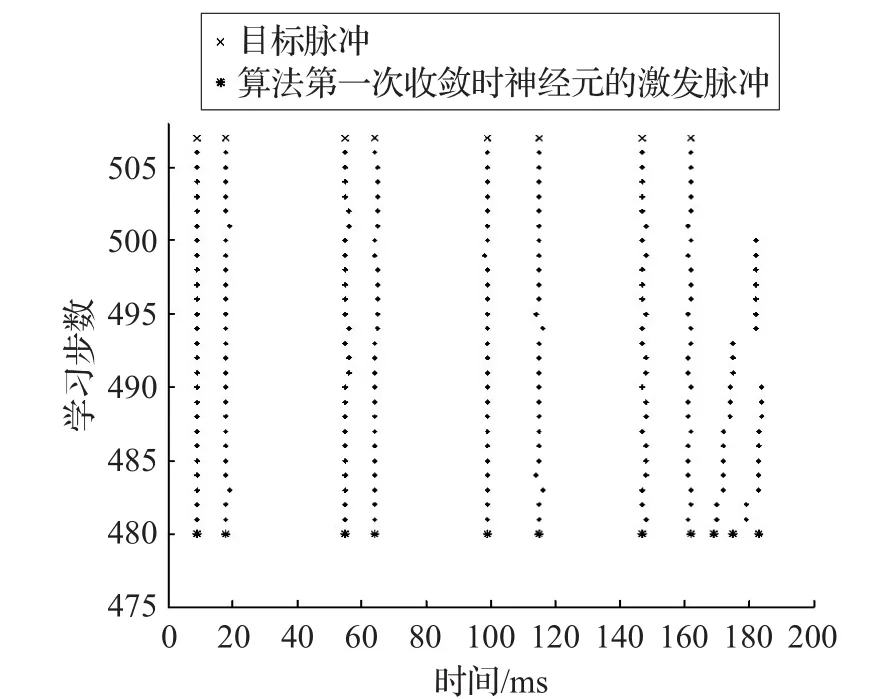
图9 V1-MSGDB从480步到506步学习过程示意图（激发个数多余）

图8 显示出神经元在480步时达到精度1，但从图9中可以看出此刻神经元激发了11个输出脉冲，比目标输出序列多了3个脉冲。V1-MSGDB采用虚拟脉冲继续调整权值，并在506步时消除了所有多余的输出脉冲达到精度1。此例中输出神经元个数差异数达到3个，但算法仍能够逐一消除输出脉冲的个数差异。从图9中可以看出算法在纠正过程中是逐个消除多余输出的脉冲的。V1-MSGDB的纠正学习过程中，有5次达到精度1，分别是：482、487、490、493、500步，但这些时刻神经元仍然均有多余的输出脉冲，因此算法持续调整权值直到精确激发出目标序列。

图10、11展示了V2-MSGDB在的学习过程，可以看出算法总共花了635步精确收敛到精度1比V1-MSGDB的学习效率稍低。这也说明了虽然V2-MSGDB从算法开始就一直纠正输出脉冲个数不同的情况，但这并不意味着该算法就能获得更好的学习效果。

同样对于实验二，也分别采用了不同的虚拟脉冲取值来学习，表2为相应的结果。在实验二中，不同的虚拟脉冲取值仍然会带来不同的收敛速度且并无明显规律。对于V1-MSGDB算法，不同的取值带来的收敛速度差异并不是太大，而对于V2-MSGDB算法差异则较大。因此最优虚拟脉冲的取值受到多个因素影响比较困难确定，需要进一步深入研究。

图10 V2-MSGDB学习精度变化示意图（激发个数多余）

图11 V2-MSGDB学习过程示意图（激发个数多余）

表2 不同取值虚拟脉冲的收敛步数（实验二）

V1-MSGDB和V2-MSGDB均能使得神经元激发出精确的目标输出序列，但在不同的情况下有着不同的学习效率。在该算法的实际应用中，一个神经元在正常学习结束之前，是无法得知它是否会收敛到一个输出脉冲个数不等的情况。因此如果采用V1-MSGDB算法，则对原来就能够正确激发的神经元学习过程无影响，而如果采用V2-MSGDB则很有可能会改变原来就能正确激发的神经元的学习轨迹。以下通过两组实验来进一步验证这两种不同的精确学习算法的效果。第一组实验采用和实验一类似的设置，不同的是神经元的初始权值是在区间[0，0.5]中产生，这种设置可以使得神经元的初次激发个数大约是目标输出脉冲个数的两倍左右。使用这种方式产生50组不同的初始权值，并分别用MSGDB、V1-MSGDB和V2-MSGDB训练该神经元。首先，在这50次实验中，MSGDB算法出现了31次收敛于不相等输出脉冲个数的现象，出现概率高达62%，这也说明当初始输出与目标输出相差较大时，MSGDB是有大概率出现收敛于不相等输出的现象。图12分三组不同情况分别列出了50次实验的平均结果，其中A组结果显示的是所有这50次实验的平均结果，B组显示的是所有出现收敛于不相等输出脉冲个数情况的实验结果，C组显示的是所有未出现收敛于不相等输出脉冲个数情况的实验结果。

图12 初次激发个数大约是目标输出脉冲个数的两倍时MSGDB、V1-MSGDB和V2-MSGDB的平均收敛步数

可以看出，在考虑所有50次实验时，带虚拟激发脉冲的算法显然需要更多的学习步数达到收敛，而MSGDB虽然只需要约264步的平均收敛步数，但超过一半是收敛于不相等的输出脉冲个数情况。当处理收敛于不相等输出脉冲个数的现象时V2-MSGDB的学习效率稍高于V1-MSGDB。而在本来就能被MSGDB精确学习的情况下V2-MSGDB则需要额外的学习步数达到收敛，这是由于V2-MSGDB算法破坏了原来学习的结果。

第二组实验使用在区间[0，0.15]的初始权值，这种设置可以使得初次激发的脉冲个数大约是目标输出脉冲个数的一半左右。同样，利用不同的初始权值进行了50次实验。在这组实验中，MSGDB算法出现了32次收敛于不相等输出脉冲个数的现象，概率仍然高达64%，这与前一组实验结果是基本一致的。从图13中可以看出不同于前一组实验结果，V2-MSGDB在这三组情况下均为学习效率最低的，当处理不能精确激发的情况时，V2-MSGDB也有可能需要更多的学习步数。

图13 初次激发个数大约是目标输出脉冲个数的一半时MSGDB、V1-MSGDB和V2-MSGDB的平均收敛步数

从以上结果可以看出，在MSGDB本来能够激发出精确的输出脉冲时，由于V2-MSGDB采用了虚拟激发脉冲纠正学习，破坏了原有学习结果，因此需要更多学习步数，而当神经元不能精确激发时，V1-MSGDB和V2-MSGDB的学习效率并没有明显的好坏区别，在不同情况下有着不同的结果。而实际应用中，并不能事先判断出学习是否会收敛于不相等的输出序列，因此综合考虑V1-MSGDB这种形式的精确序列学习算法更具有优势。

5 结束语

本文主要针对多脉冲神经元梯度下降学习算法MSGDB的固有缺陷进行改进，使得神经元通过样本学习后能够激发出和目标序列个数一致的精确脉冲序列。该算法引入虚拟激发脉冲来构建误差函数，不但能解决激发个数多余的问题还能解决激发个数不足的问题。同时本文提出的精确序列算法也在解决输入、输出个数差异较大时同样能获得较好的学习效果。

本文的后续工作将对如何确定最优的虚拟脉冲激发时间展开进一步研究，并将其结果延伸到脉冲神经网络的学习算法研究中。