新型软亚BCI-代数的进一步研究
黄 昱,廖祖华,李 论
1.无锡太湖学院,江苏 无锡 214064
2.江南大学 理学院,江苏 无锡 214122
3.中国科学院 数学与系统科学研究院,北京 100190
1 引言
逻辑代数是人工智能、逻辑电路设计、计算机推理等领域的逻辑基础。BCK/BCI-代数作为两类重要的逻辑代数,是由Imai和Iseki[1-2]于1966年提出的。BCI-代数是BCK-代数的推广。BCK/BCI代数自引入以来,得到了许多学者的扩展研究[3-7]。2005年,陈露和蒲义书[8]推广了BCI-代数,提出了亚BCI-代数及其理想的概念。2010年,彭家寅[9]引入了亚BCI-代数的模糊理想的概念并讨论了相关性质。
软集理论是Molodtsov[10]于1999年创立的。它是处理不确定性问题的一个有力的数学工具。其理论已被应用于不确定决策、近似推理、软计算、数据分析等[11-16]诸多领域。将软集与代数系统相融合是研究的热点之一。Aktas和Cagman[17]率先将软集与群论相结合提出了软群的概念。Jun[18]提出了软BCK/BCI-代数的概念。伏文清等[19-20]进一步把软集思想应用于BCK代数,研究了软BCK代数的运算性质。刘春辉[21]将软集概念及其相关运算运用于FI代数,提出滤子化软FI代数并讨论其代数性质。彭家寅[22]利用软集理论去处理BCC-代数的结构,讨论了软BCC-理想与理想的软BCC-代数。
2008年,温永川[23]将参数集赋予群的代数结构,提出了新型软群的概念。这种将参数集赋予代数结构的方法引入的软集代数可以得到更深刻的结果。廖祖华的团队利用这一思想,研究了一系列新的软集代数[24-27]。2014年,Jun等[28-29]将犹豫模糊集引入MTL-代数和BCK/BCI代数中,开创了犹豫模糊代数的新领域。接着,国内外学者获得了一系列研究成果[30-35]。值得指出的是犹豫模糊代数的研究是这种新型软集代数的特例(泛集U=[0,1]时的情形)。对于一般的U,文献[23]引进的对偶软集是与犹豫模糊集的α-水平集不同的代数结构。某种代数的模糊子集是某种犹豫模糊代数的充要条件是犹豫模糊集的α-水平集是某种代数。而本文的研究表明某种代数的软集是某种新型软代数的充要条件是对偶软集是某种代数,但与α-水平集是某种代数不等价(相关论文A new type soft prime ideal of KU-algebras已被斯普林格出版社Advances in Intelligent and Soft Computing录用)。因此U取一般集合是有研究意义的。
文献[27]将参数集赋予亚BCI-代数,给出了新型软亚BCI-代数的新概念,并研究了两个新型软亚BCI-代数的且运算及限制交仍然是新型软亚BCI-代数。利用对偶软集给出了新型软亚BCI-代数的等价刻画。同时还给出了新型软亚BCI-代数的同态像与原像的性质。
本文在文献[27]的基础上对新型软亚BCI-代数做了进一步研究。
2 预备知识
本章给出了文中需要的软亚BCI-代数、软集的相关知识。
定义1[8](亚BCI-代数)一个(2,0)型代数(X,∗,0)如果满足条件:∀x,y,z∈X,有:
(1)x∗0=x ;
(2)x∗x=0 ;
(3)(x∗y)∗z=(x∗z)∗y 。则称X为一个亚BCI-代数。
定义2[8](亚BCI-代数的子代数)亚BCI-代数X的非空子集S称为 X的子代数,如果对∀x,y∈S,有x∗y∈S 。
注1任意子代数 S都包含0,因为 ∀x∈S,有0=x∗x∈S。
定义3[10](软集)设U是一个初始集合,E是参数集,A⊆E,P(U)是U的幂集,设F:A→P(U)为一个映射,则称(F,A)是U上的软集,也称F为A的软集。
定义4(笛卡尔积)设A,B是两个非空集合,称A×B={(x,y)|x∈A,y∈B}为A,B的笛卡尔积。
定义5[36](软集的且运算)(F,A),(G,B)是U上的软集,令 (F,A)∧(G,B)=(H,A×B),其中 H(x,y)=F(x)⋂G(y),∀(x,y)∈A×B ,则称 (F,A)∧(G,B)是软集 (F,A)与(G,B)的且运算。
定义6[27](新型软亚BCI-代数)设X为一个亚BCI-代数,H:X→P(U)为一个软集,若∀x,y∈X,满足H(x∗y)⊇H(x)⋂H(y),则称 H 为 X的一个新型软亚BCI-代数,记为 (H,X)。
引理1[27]H为X的一个新型软亚BCI-代数,则∀x∈X ,有 H(0)⊇H(x)。

3 新型软亚BCI-代数的一些新性质
本章给出两个亚BCI-代数的并代数、并代数上的扩展交以及软平移等新概念,讨论新型软亚BCI-代数在并代数上的扩展交、软平移以及投影等基本性质。
定义8 设 (X1,∗1,0)与 (X2,∗2,0)是两个亚 BCI-代数,又设 X=X1⋃X2,且X1⋂X2={0},在X上定义运算∗如下:
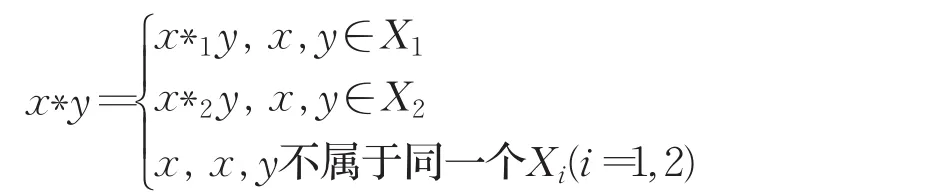
记 X=X1⊕X2。
注2由定义x,y在X1与X2的并集中取元素,所以x∗y在X1⊕X2中的运算结果与它在X2⊕X1中的运算结果相同。因此X1⊕X2=X2⊕X1。
引理2 设 (X1,∗1,0)与 (X2,∗2,0)是两个亚 BCI-代数,若 X=X1⊕X2,则 (X,∗,0)是一个亚BCI-代数。这时称 (X,∗,0)为 (X1,∗1,0)与 (X2,∗2,0)的并代数。
证明∀x∈X=X1⋃X2,有 x∈X1或 x∈X2。若x∈X1,则 x,0∈X1,由定义得,x∗0=x∗10=x 及x∗x=x∗1x=0。若 x∈X2,则 x,0∈X2,由定义得,x∗0=x∗20=x及 x∗x=x∗2x=0。
∀x,y,z∈X=X1⋃X2,
(1)若 x∈X1,y∈X1,z∈X1,由定义1得 (x∗y)∗z=(x∗z)∗y 。
(2)若 x∈X1,y∈X1,z∈X2,有(x∗y)∗z=(x∗1y)∗z=x∗1y ,(x∗z)∗y=x∗y=x∗1y ,得 (x∗y)∗z=(x∗z)∗y 。
(3)若x∈X1,y∈X2,z∈X1,有(x∗y)∗z=x∗z=x∗1z,(x∗z)∗y=(x∗1z)∗y=x∗1z ,得 (x∗y)∗z=(x∗z)∗y 。
(4)若 x∈X1,y∈X2,z∈X2,有 (x∗y)∗z=x∗z=x ,(x∗z)∗y=x∗y=x ,得 (x∗y)∗z=(x∗z)∗y 。
(5)若 x∈X2,y∈X1,z∈X1,有 (x∗y)∗z=x∗z=x ,(x∗z)∗y=x∗y=x ,得 (x∗y)∗z=(x∗z)∗y 。
(6)若x∈X2,y∈X1,z∈X2,有(x∗y)∗z=x∗z=x∗2z,(x∗z)∗y=(x∗2z)∗y=x∗2z ,得 (x∗y)∗z=(x∗z)∗y 。
(7)若 x∈X2,y∈X2,z∈X1,有(x∗y)∗z=(x∗2y)∗z=x∗2y ,(x∗z)∗y=x∗y=x∗2y ,得 (x∗y)∗z=(x∗z)∗y 。
(8)若 x∈X2,y∈X2,z∈X2,由定义1得 (x∗y)∗z=(x∗z)∗y 。
综上所述,(X,∗,0)是一个亚BCI-代数。
例1 设 X1={0,1},定义“ ∗1”,其运算表如表1。容易验证(X1,∗1,0)是亚BCI-代数,它的子代数有{0},{0,1}。

表1 运算“ ∗1”
设 X2={0,2,3},定义“ ∗2”,其运算表如表2。容易验证 (X2,∗2,0)是亚 BCI-代数,它的子代数有{0},{0,2},{0,2,3}。

表2 运算“ ∗2”
则由X=X1⊕X2的运算定义知X的运算“∗”如表3。

表3 运算“∗”
由引理2知(X,∗,0)是亚BCI-代数,它的子代数有{0},{0,1},{0,2},{0,1,2},{0,2,3},{0,1,2,3}。
定义9设X1,X2是两个亚BCI-代数,(H1,X1),(H2,X2)是U上的软集,若软集(H,X)满足:
(1)X=X1⊕X2;



在一定条件下,有下面的定理。

证明因为 X1⋂X2={0},故∀x∈X1⊕X2,有:

(1)若 x,y∈X1-X2,则 H(x)=H1(x),H(y)=H1(y),如果 x∗y≠0,则 x∗y=x∗1y∈X1-X2,因为 H1是 X1的新型软亚 BCI-代数,故 H(x∗y)=H1(x∗1y)⊇H1(x)⋂H1(y)=H(x)⋂H(y)。
在伟晶作用发育的全过程中,不是所有伟晶岩区的伟晶岩脉中都可以见到伟晶岩各结构带,只在一些典型的脉中能够见到。特别是构造活动频繁、围岩渗透性较强的地区形成的伟晶岩,往往不具有良好的带状构造,各种矿物组合在脉中分布无明显的规律[9]。
如果 x∗y=0 ,则 H(x∗y)=H1(0)⋂H2(0),因为 H1是 X1的新型软亚BCI-代数,故 H1(0)⊇H1(x)=H(x),H2(0)=H1(0)⊇ H1(y)=H(y),即 H(x∗y)⊇H(x)⋂H(y)。
(2)若 x,y∈X2-X1,同理可证 H(x∗y)⊇H(x)⋂H(y)。
(3)若x∈X1-X2,y∈X2-X1,则x∗y=x,H(x∗y)=H(x)⊇H(x)⋂H(y)。
(4)若x∈X2-X1,y∈X1-X2,则x∗y=x,H(x∗y)=H(x)⊇H(x)⋂H(y)。
(5)若 x∈X1-X2,y∈X1⋂X2={0},则 x∗y=x∗0=x,H(x∗y)=H(x)⊇H(x)⋂H(y)。
(6)若 x∈X2-X1,y∈X1⋂X2={0},则 x∗y=x∗0=x,H(x∗y)=H(x)⊇H(x)⋂H(y)。
(7)若 x∈X1⋂X2={0},y∈X1-X2,则 x∗y=0∗1y。
如果0∗1y∈X1-X2,因为H1是X1的新型软亚BCI-代 数,故 H(x∗y)=H(0∗1y)=H1(0∗1y)⊇H1(0)⋂H1(y)=H1(y)=H(y)⊇H(x)⋂H(y)。
(8)若 x∈X1⋂X2={0},y∈X2-X1,则 x∗y=0∗2y。如果0∗2y∈X2-X1,因为H2是X2的新型软亚BCI-代数,故 H(x∗y)=H(0∗2y)=H2(0∗2y)⊇H2(0)⋂H2(y)=H2(y)=H(y)⊇H(x)⋂H(y)。
如 果 0∗2y=0 ,则 H(x∗y)=H(0)=H1(0)⋂H2(0)=H2(0)⊇H2(y)=H(y)⊇H(x)⋂H(y)。
(9)若 x,y∈X1⋂X2={0},则 x=y=0,故 x∗y=0,H(x∗y)=H(0)=H(0)⋂H(0)=H(x)⋂H(y)。
综上所述,H是X1⊕X2的新型软亚BCI-代数。
定理2设 XH:={x|x∈X,H(x)=H(0)},如果H为X的一个新型软亚BCI-代数,则XH为X的子代数。
证明显然0∈XH,所以XH为X的非空子集。又∀x,y∈XH,有H(x)=H(y)=H(0),因H 是X 的新型软亚BCI-代数,有 H(x∗y)⊇H(x)⋂H(y)=H(0),又由引理1知 H(0)⊇H(x∗y),进而有 H(x∗y)=H(0),即 x∗y∈XH,所以,XH是X的子代数。
定义10设X是任一参数集,H:X→P(U)是一个软集,λ∈P(U),对于∀x∈X,Htλ(x)=H(x)⋃λ称为H相对于λ的一个软平移。
定理3设X为亚BCI-代数,H:X→P(U)为一个软集,λ∈P(U),若H是X的新型软亚BCI-代数,则H相对于λ的软平移Htλ是X的新型软亚BCI-代数。
证明∀x,y∈X,有:


证明若存在λ⊆ΣH使得H相对于λ的软平移是X的新型软亚BCI-代数,则有∀x,y∈X,,即H(x∗y)⋃λ⊇(H(x)⋃λ)⋂(H(y)⋃λ)=[H(x)⋂H(y)]⋃λ。∀z∈H(x)⋂H(y),有z∈[H(x)⋂H(y)]⋃λ⊆H(x∗y)⋃λ。因为 z∉λ,所以 z∈H(x∗y),即 H(x)⋂H(y)⊆H(x∗y)。
因此,H是X的新型软亚BCI-代数。
定理5设X1,X2为两个亚BCI-代数,若(F,X1)和(G,X2)分别为X1和X2的软集,且(H,X)=(F,X1)∧(G,X2)是 X的新型软亚BCI-代数,则(HX1,X1)和(HX2,X2)分别是X1和X2的新型软亚BCI-代数。
证明∀x,y∈X1,有:


所以,(HX1,X1)是X1的新型软亚BCI-代数。同理可证(HX2,X2)是X2的新型软亚BCI-代数。
4 新型软亚BCI-代数的一些新的等价刻画
本章给出亚BCI-代数上的两个软集的合成运算的新概念,同时利用软集的合成运算、水平集、广义特征函数给出新型软亚BCI-代数的新的等价刻画。
定义11设(F,A)是A上的软集,(G,B)是B上的软集,若满足:
(1)A⊆B;
(2)∀x∈A,有 F(x)⊆G(x)。
注3 显然,若且,则(F,A)=(G,B)。
定义12设X是亚BCI-代数,(F,X)和(G,X)分别为X的两个软集。定义(F∘G,X):

则(F∘G,X)是X的软集,并称F∘G为两个软集的合成。
因∀z∈X,z∗0=z,于是 X中的元素均有分解式x∗y=z成立,所以上述定义是合理的。
定理6设X为亚BCI-代数,H:X→P(U)为一个软集,则H是X的新型软亚BCI-代数的充要条件是(H2,X)=(H,X)。


定理7设X为一个亚BCI-代数,H:X→P(U)为一个软集,则H是X的新型软亚BCI-代数的充要条件是 H 的 α -水平集 Hα:={x|H(x)⊇α,α∈P(U)}≠∅ 是X的子代数。
证明必要性:∀x,y∈Hα,则 H(x)⊇α,H(y)⊇α,由 H 是 X 的新型软亚BCI-代数,知 H(x∗y)⊇H(x)⋂H(y)⊇α,即 x∗y∈Hα,所以,Hα是 X 的子代数。
充分性:∀x,y∈X ,若 H(x)⋂H(y)=∅,则 H(x)⋂H(y)⊆H(x∗y);若 H(x)⋂H(y)≠∅ ,令 H(x)⋂H(y)=α,有H(x)⊇α且H(y)⊇α,那么,x∈Hα且y∈Hα。由Hα≠∅ 是 X 的子代数,知 x∗y∈Hα,进而有 H(x∗z)⊇α=H(x)⋂H(y)。
因此,H是X的新型软亚BCI-代数。
定义13 设X 是亚BCI-代数,X1是X 的子集,X→P(U)是一个软集,γ1,γ2∈P(U),γ2⊂γ1,且满足:

定理8设X为亚BCI-代数,X1是X的非空子集,则 X1是 X的子代数的充分必要条件是是 X的新型软亚BCI-代数。
证明必要性:∀x,y∈X,若x∉X1或 y∉X1,则有或,所以,。若 x,y ∈ X1,因 X1是 X 的子代数,有 x∗y∈ X1,故H X1(γ1,γ2)(y)。
5 结束语
本文是文献[27]研究工作的继续。引入了两个亚BCI-代数的并代数,这对亚BCI-代数本身研究也很有意义。由此产生了两个软集在并代数上的扩展交的新概念。另外还引入了软集的软平移、合成运算,利用这些代数结构对新型软亚BCI-代数进行了新的刻画。值得指出的是当U=[0,1]时,就得到了相应的犹豫模糊亚BCI-代数的结果(犹豫模糊集时的情形也未见研究)。进一步会用上述的这些代数结构去研究其他的逻辑代数的相关性质。

