信用评价方法的多维最优选择策略

杨成荣，李战江，史来银,2

（1.内蒙古农业大学 经济管理学院；2.内蒙古银行总行，内蒙古 呼和浩特 010010）

0 引言

现有研究中单一信用评价方法的研究较多，比如德尔菲法、人工神经网络法、层次分析法、Fisher判别法、5C要素分析法、模糊数学法、支持向量机法和Logistic回归法等，但是在何种情况下使用何种方法是困扰很多学者的难题，而现有研究针对最优信用评价方法选择问题的研究少之又少。因此研究多种信用评价方法的最优选择具有重要的科研价值。

信用评价方法的多维最优选择策略是指在不同维度下给出每一维度的多种信用评价方法优劣排序以及最优选择。目前已有研究存在的不足之处：一是单一信用评价方法的研究较多，但是没有对众多信用评价方法进行优劣比较。二是在现有信用评价a研究中没有在多维度下筛选出最优评价方法。本文将现有信用评价方法分为五类，分别为计量经济学方法、多元统计方法、人工智能方法、非参数方法以及数学优化方法，在每一类信用评价方法中选取一种高频研究方法，分别为：Logistic回归方法、Fisher判别方法、支持向量机方法、K最近邻方法以及灰色关联方法，使用这五种信用评价方法从判对率维度、软件操作维度以及适用范围维度进行优劣比较从而得到每个维度下的最优信用评价方法，最后以企业信贷数据为基础进行应用。

1 信用评价的方法

1.1 信用评价指标的标准化

（1）正向指标的标准化

设：xij是第i个企业第j个指标的标准化值；vij是第i个企业第j个指标的原始数值；n是企业样本总数。则正向指标标准化值xij为[1]：

（2）负向指标的标准化

设：xij是第i个企业第j个指标的标准化值；vij是第i个企业第j个指标的原始数值；n是企业样本总数。则负向指标的标准化值xij为[1]：

（3）定性指标的标准化

定性指标的标准化规则如表1所示。

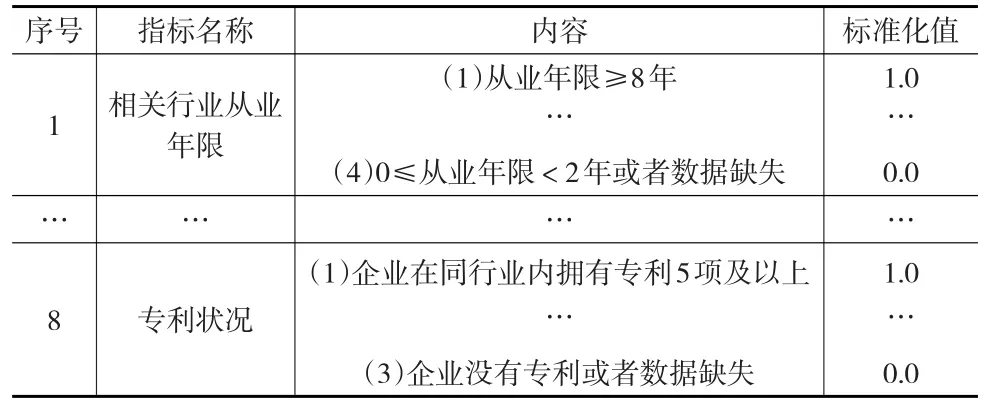
表1 定性指标的标准化规则

1.2 计量经济学方法——Logistic回归法

1.2.1 Logistic回归法原理

设：Pi是第i个企业样本的概率；bj是第j个评价指标的偏回归系数；xj是第j个评价指标的数值；yi是第i个样本的信用违约状态(yi=0则表示样本为非违约；yi=1则表示样本为违约）；pi是第i个样本的条件概率(yi=0时Pi=pi；yi=1时Pi=1-pi)。则有Logit模型为[2]：

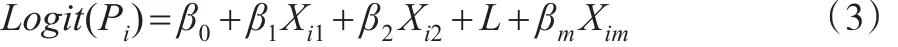
即：

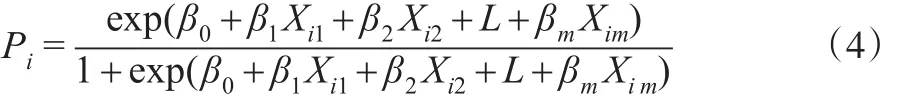
则n个样本的联合密度函数的似然函数为[3]：

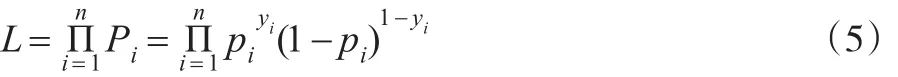
取对数化简为对数似然函数：

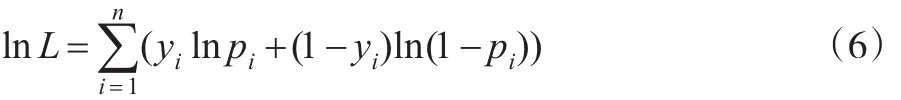
使对数似然函数最大以求解参数的估计值：

1.2.2 Logistic回归法的分类标准

Logistic模型中Pi越接近0则表示企业违约的可能性越大，Pi越接近1则表示企业非违约的可能性越大，本文将判定企业样本是否违约的分界值设置为0.5，即若待判样本的P值大于0.5则判定该样本非违约，若待判样本的P值小于0.5则判定该样本违约。

1.3 多元统计方法——Fisher判别法

1.3.1 Fisher判别法原理

设：u(x)是判别函数；αj是第j个评价指标的系数；xj是第j个评价指标的数值；p是指标个数；α是评价指标的系数向量；k是总体的个数；ni是第i个总体中抽取的样本量；uˉi是判别函数在第i个总体的样本均值；uˉ是判别函数的总体样本均值；A是组间离差平方和；E是组内离差平方和；xˉi是第i个总体的样本均值向量；是判别函数在第i个总体的样本方差；si是第i个总体的样本协方差阵；xˉ是样本总体均值向量；x是评价指标的数值向量。则建立的Fisher判别函数为[4]：

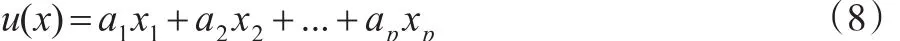
根据Fisher判别分析的基本思想，选择a′=(a1，...，ap)使λ最大[4]：

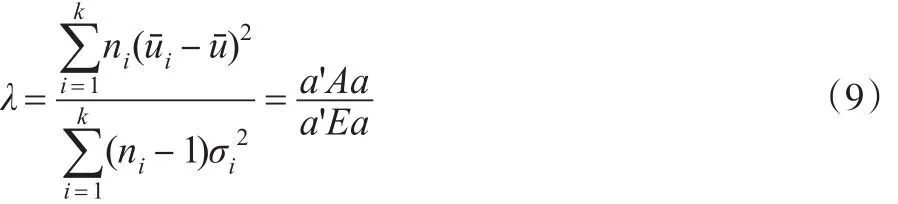
其中：

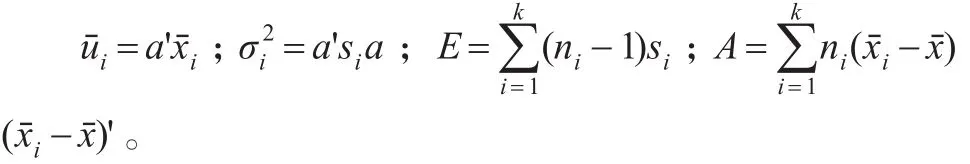
1.3.2 Fisher判别法的分类标准

1.4 人工智能方法——支持向量机法

1.4.1 支持向量机法原理

设：是第i个企业的违约状态预测值(：第i个企业违约状态预测为非违约：第i个企业违约状态预测为违约）；n是企业样本总数；aj是支持向量机训练所得的拉格朗日因子；yi是第i个企业的违约状态真实值；k(xi，xj)是核函数；xi是第i个企业的评价指标；b是阂值；σ是核函数的参数。为[5]：

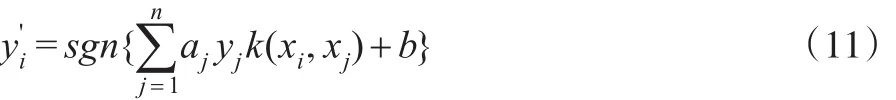
其中，aj和b由下式求得[5]：

其中：

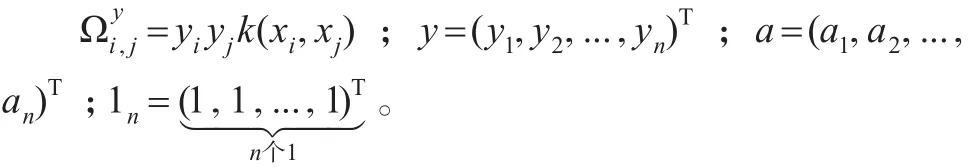
选择高斯径向基核函数为支持向量机的核函数，则有[6]：

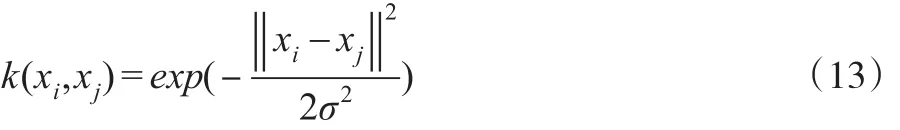
1.4.2 支持向量机法的分类标准根据最终得到的第i个企业的违约状态预测值得到支持向量机法下的分类标准：当，表明第i个企业被预测为非违约；当，表明第i个企业被预测为违约。

1.5 非参数方法——K最近邻法

1.5.1 K最近邻法的原理

假定有c个类别为w1，w2，…，wc的样本集合，每类有标明类别的样本Ni个，共计个样本点。设样本的指标有m个，则样本点的指标将可以构成一个m维特征空间，所有的样本点在这个m维特征空间里都有惟一的点与它对应，则对任何一个待判别样本x=(u1，u2，…，um)，计算它与所有的样本点xi的Euclidean距离[7]：

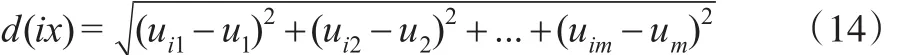
1.5.2 K最近邻法的分类标准

由式（14）可以得到n个距离，通过比较这n个距离找出最小的k个距离对应的样本点，假设其中有k1个属于非违约样本点，k2个属于违约样本点(kl+k2=k，k为奇数)，且有k1大于(或小于)k2，则待识别样本x属于非违约样本（或违约样本）。

1.6 数学优化方法——灰色关联法

1.6.1 灰色关联法的原理

（1）灰色关联系数的计算

设：xij是待判别信用类别的企业i的第j个指标的数值；xkj是参考对象k（k=0时取非违约企业样本的聚类中心；k=1，取违约企业样本的聚类中心）的第j个指标的数值；ξ(xij，xkj)是待判别信用类别的企业i与参考对象k间的灰关联系数；ρ是分辨系数（一般取0.5）。则有[8]：

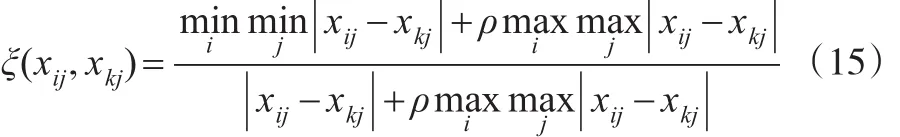
（2）灰色关联度的计算

本文通过基于群灰色关联度的方法给各指标进行赋权，以求待判别信用类别的企业样本与违约、非违约两类企业样本聚类中心的考虑权重的灰色关联度，进而进行企业信用类别的判别。

设：γ(xi，xk)是待判别信用类别的企业i与参考对象k间的灰色关联度；m是指标个数；ωj是第j个指标的权重；ξ(xi，xk)是待判别信用类别的企业i与参考对象k间的灰关联系数；xj是第j个指标的数值；xˉj是除第j个指标外的剩余指标的数值；γ(xj，xj)是第j个指标和除第j个指标外的剩余指标的群灰色关联度；n是企业总数；xij是待判别信用类别的企业i的第j个指标的数值；ξ(xij，xia)是第j个指标与第a个指标间的灰关联系数；ρ是分辨系数。则第i个企业与参考对象k间的灰色关联度为[8]：

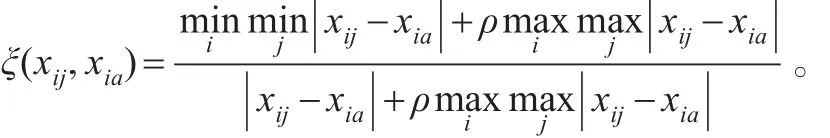
1.6.2灰色关联法的分类标准

若待判别信用类别的企业样本与违约类企业样本灰色关联度＞待判别信用类别的企业样本与非违约类企业样本灰色关联度，则待判别信用类别的企业违约；若待判别信用类别的企业样本与违约类企业样本灰色关联度＜待判别信用类别的企业样本与非违约类企业样本灰色关联度，则待判别信用类别的企业非违约。

1.7 多维度的最优选择标准

本文从评价方法的判对率维度、软件操作维度以及适用范围维度来衡量多种信用评价方法的优劣。

1.7.1 判对率维度

设：A是信用评价方法的判对率；n0是非违约企业样本总数；yi是第i个企业的违约状态真实值(yi=0：第i个企业违约状态真实为非违约；yi=1：第i个企业违约状态真实为违约）；是第i个企业的违约状态预测值；n1是违约企业样本总数；n是企业样本总数。则信用评价方法的判对率A为：

式（17）分子第一项表示非违约企业被鉴定正确的数量，分子第二项表示违约企业被鉴定正确的数量。公式含义为：预测企业样本违约、非违约时违约企业、非违约企业被鉴定正确的比率。

1.7.2 软件操作维度

本文主要针对在软件操作过程中参数的设置、软件操作的难易度以及软件运行时长来对各个评价方法的软件操作方面进行讨论：

（1）在参数的设置中主要考虑参数确定的难易度、设置的参数个数以及设置的参数对结果的影响度这三个方面，若参数的确定越简易、设置的参数个数越少、设置参数的不同对评价结果影响程度越小则该评价方法越好；

（2）在软件操作的难易度中主要考虑算法的实现是否需要编程运行、若无需编程则考虑软件操作的步骤数、若需要编程则考虑编程的难易度，若无需编程且软件操作的步骤数越少则该评价方法越好，相反若需要编程且软件操作的步骤数越多则该评价方法越欠佳；

（3）在软件运行时长中主要考虑算法实现所需时间的长短，若算法实现所需时间越短则该评价方法越好。

1.7.3 适用范围维度

不同信用评价方法有不同适用范围，本文根据方法适用范围的广泛度对信用评价方法进行最优选择。

2 评价方法的应用

2.1 信用评价指标体系

本文选用现有研究中构建好的企业信用评价指标体系进行应用分析，该指标体系包含主营业务收入现金比率、超速动比率、资产负债率等22个评价指标，评价指标体系如表2所示[9]。

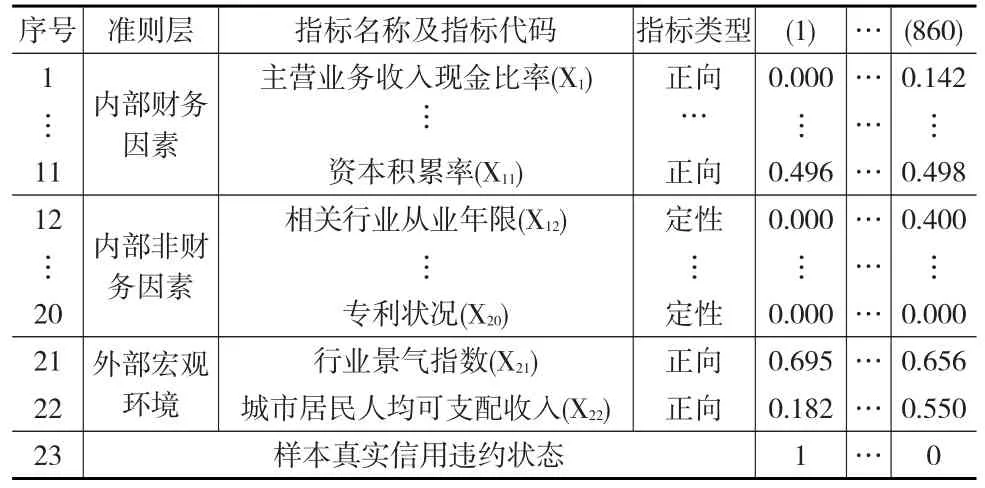
表2 信用评价指标及其标准化值

2.2 数据及信用指标的标准化

本文采用的企业信贷样本共860个，其中非违约企业样本共830个，违约企业样本共30个，表2中序号为23一行表示企业的真实信用违约状态，其中0表示该企业真实信用状态为非违约，1表示该企业真实信用状态为违约。

选用的企业信用评价指标体系及标准化值见表2所示。

2.3 计量经济学方法——Logistic回归法

本文利用SPSS软件对Logistic回归法进行应用。切割值默认为0.5、最大迭代次数默认为20次并选用向前步进(条件)法，其中步进概率中进入概率默认为0.05、删除概率默认为0.1，在0.05显著性水平下运行SPSS软件后可以得到最终模型为：

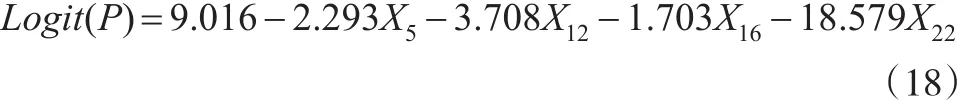
将待判样本相应于这4个指标的标准化后数据（见表3）代入式（18）可以得到各样本的P值，根据Logistic回归法的分类标准得到最终的分类结果如表4所示，判对率为97.44%。

2.4 多元统计方法——Fisher判别法

本文利用SPSS软件对Fisher判别法进行应用。由于选取的已构建好的企业信用指标体系不含信息冗余指标，所以不存在多重共线性。在先验概率相同的前提下一起输入自变量得到Fisher线性判别函数系数如表5所示。

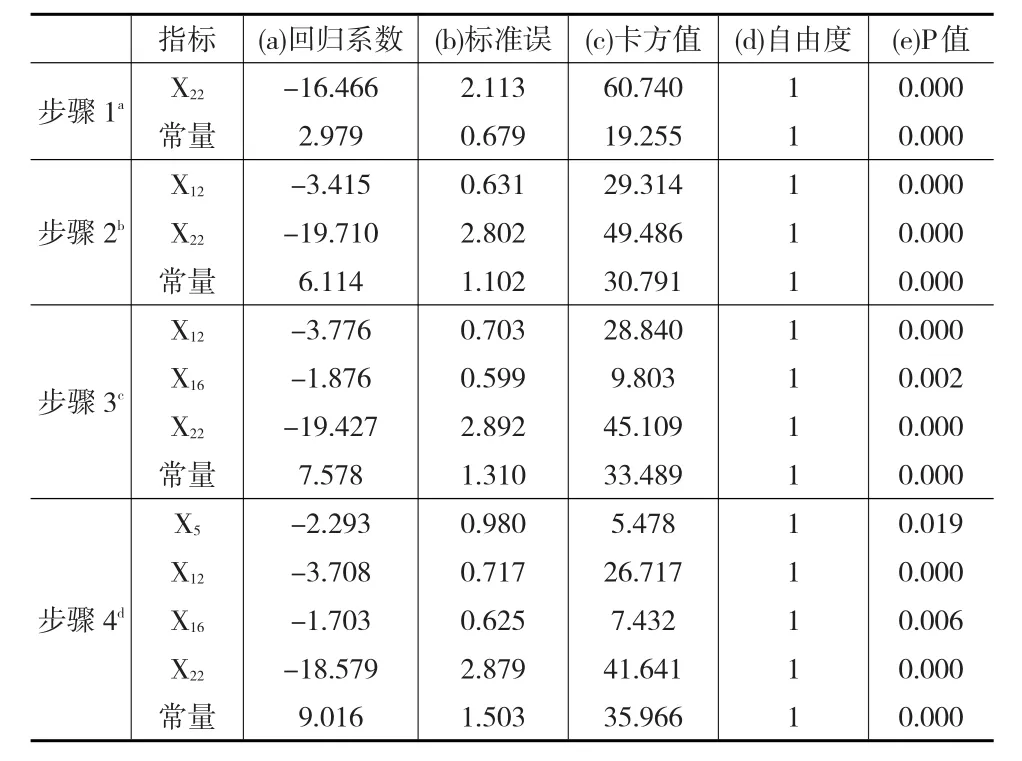
表3 方程中的变量

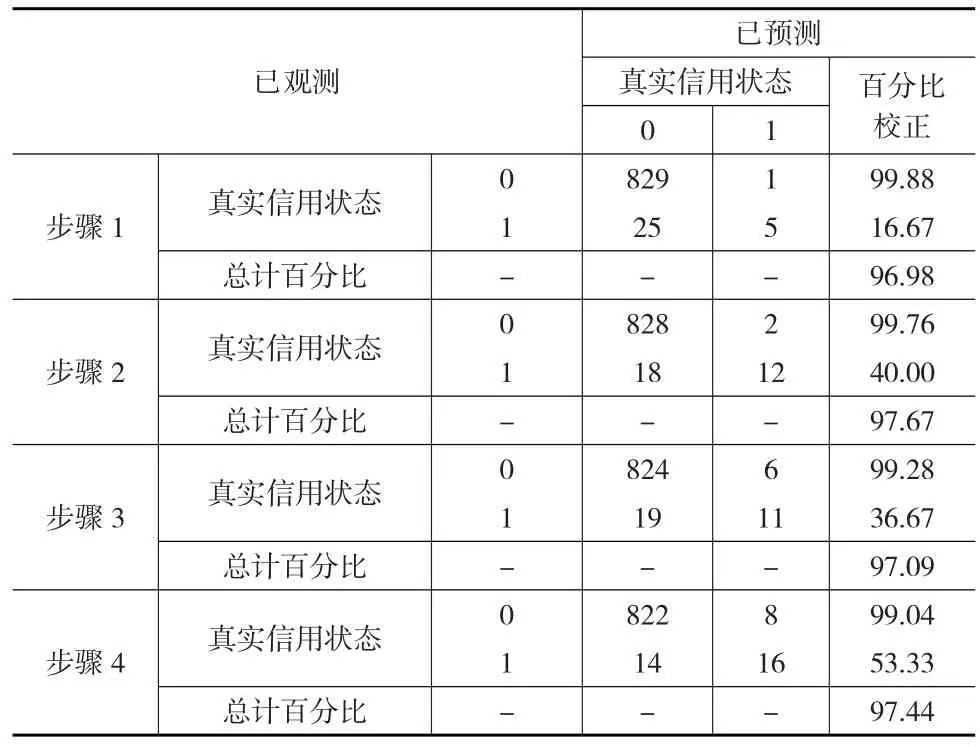
表4 Logistic回归法的分类结果

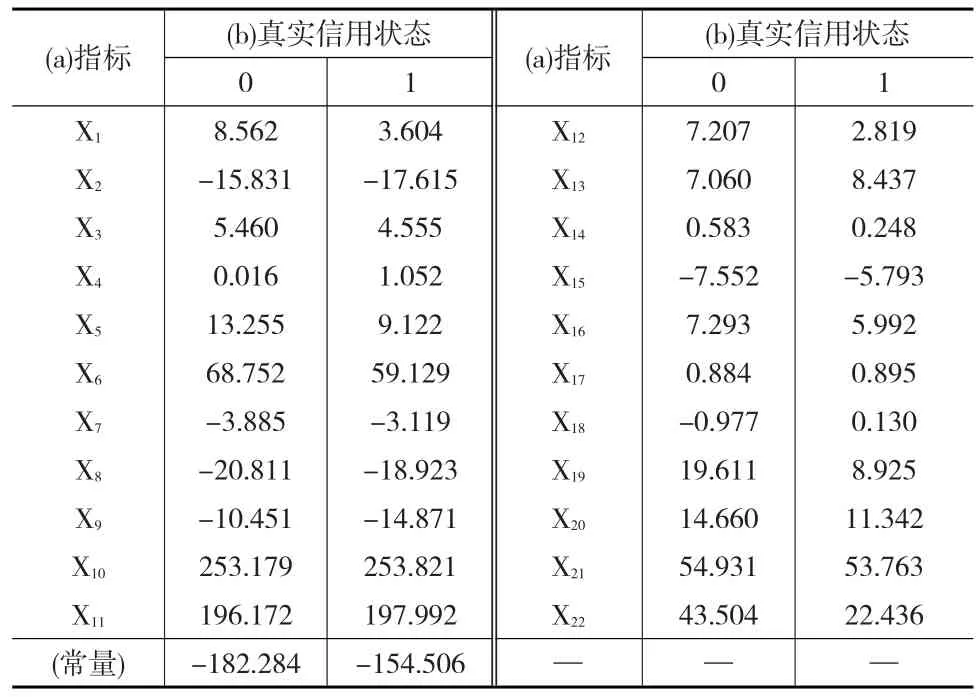
表5 Fisher线性判别函数的系数

由表5得到两个线性判别函数为：

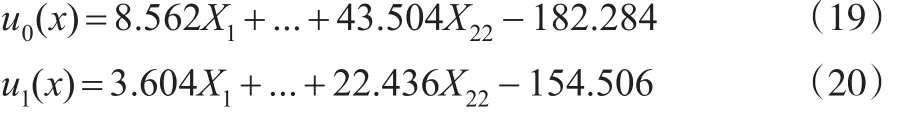
将待判样本指标的标准化后数据分别代入式（19）、式（20）计算各自判别值，然后将该待判样本判归其中最大值对应的信用违约类型。得到待判样本的分类回判结果如表6所示，得到判对率为96.16%。

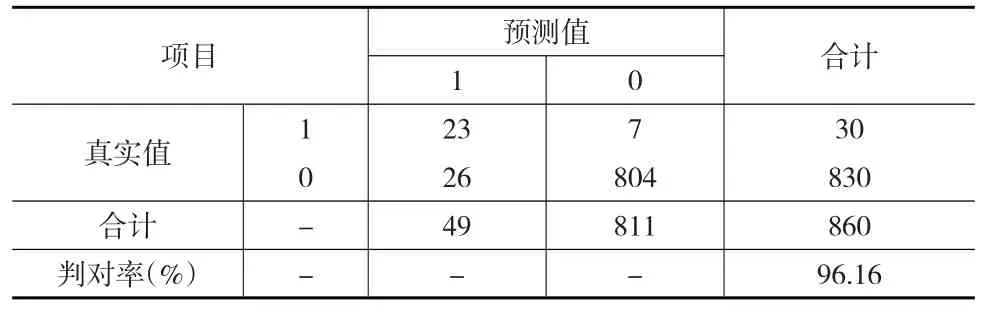
表6 Fisher判别法的分类回判结果

2.5 人工智能方法——支持向量机法

本文利用MATLAB软件和LIBSVM工具箱对支持向量机法进行应用。将860个企业样本随机按8：2的比例选取训练集、测试集，即形成由24个违约样本和664个非违约样本组成的训练集、由6个违约样本和166个非违约样本组成的测试集，并使用MATLAB软件和LIBSVM工具箱并利用工具箱中的网格参数寻优函数SVMcgForClass对惩罚系数c以步长0.5在2-8到28之间进行选择、对高斯径向基核函数参数g以步长0.5在2-8到28之间进行选择，并将交叉验证数设为3折、准确率离散化显示步长设为0.5，将设置好的参数连同选取的训练集在MATLAB中运行程序后得到最优惩罚系数c、最优高斯径向基核函数参数g分别为90.5097、0.0055243。基于最优参数c和g、使用选取好的训练集在MATLAB上建立训练模型以对测试集中样本的信用违约状态进行预测，在MATLAB上运行程序后得到如表7所示的预测结果，判对率为98.84%。

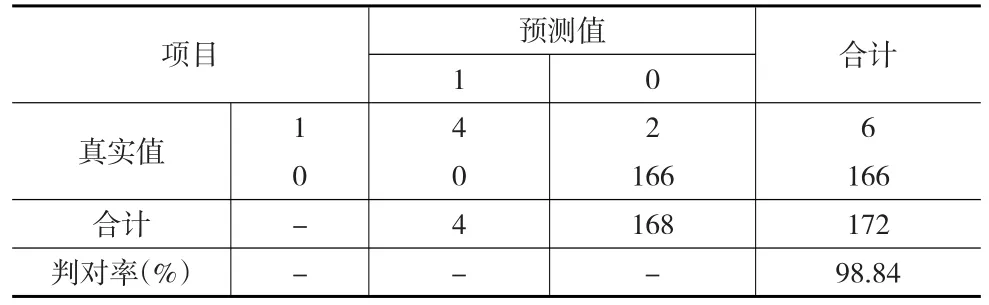
表7 支持向量机法的预测结果

2.6 非参数方法——K最近邻法

本文利用SPSS软件对K最近邻法进行应用。设置最近邻元素k的选择方式为：最大值为5、最小值为3的自动选择，样本点与聚类中心距离采用Euclidean度量方式，将训练集、测试集的分区比例设置为80%、20%，并执行10折的交叉验证，操作SPSS软件后得到样本的信用违约状态预测结果如表8所示，判对率为98.02%。

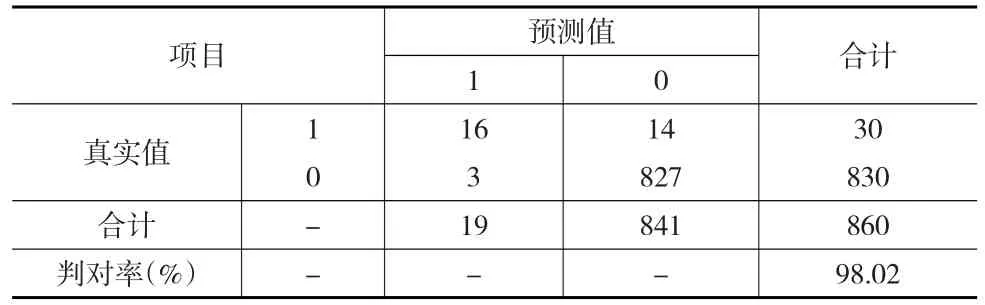
表8 K最近邻方法的预测结果

2.7 数学优化方法——灰色关联法

本文利用EXCEL、DPS软件对灰色关联法进行应用。求聚类中心时使用在建立支持向量机模型时划分好的训练集，在基于灰色关联分析的企业信用类别判别时使用在建立支持向量机模型时划分好的测试集。操作EXCEL软件后可以得到违约、非违约样本的聚类中心如表9列(b)所示。

表9 灰色关联法的聚类中心

将分辨系数设置为0.5，操作DPS软件后得到待判企业样本与违约、非违约样本聚类中心的关联度如表10列(a)、列(b)所示，根据灰色关联信用类别判别规则可以得到待判样本信用违约状态预测结果如表10列(c)所示，进而得到如表11所示的判对准确率为86.63%。

表10 灰色关联度

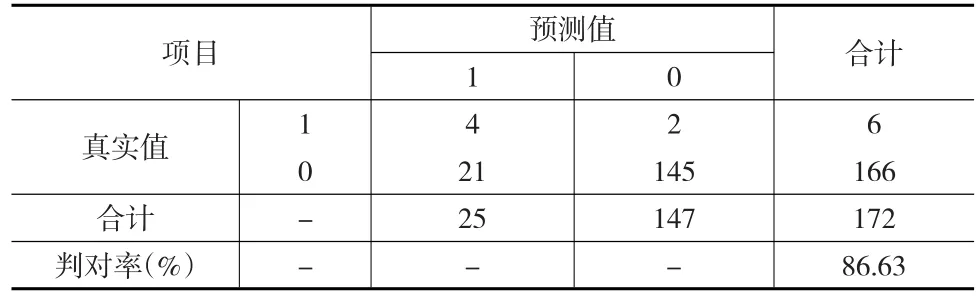
表11 灰色关联法的分类结果

2.8 多维度的最优选择策略

由下页表12得到信用评价方法的最优选择策略为：

（1）在判对率的维度下：本文选取的5种信用评价方法有以下优劣排序：支持向量机法＞K最近邻法＞Logistic回归法＞Fisher判别法＞灰色关联法，即在本文中相比其余4种信用评价方法，支持向量机法在判对率上显示出优势。

（2）在软件操作的维度下：本文选取的5种信用评价方法有以下优劣排序：Fisher判别法＞Logistic回归法＞灰色关联法＞K最近邻法＞支持向量机法，即在本文中相比其余4种信用评价方法，Fisher判别法在软件操作上显示出优势。

（3）在适用范围的维度下：本文选取的5种信用评价方法有以下优劣排序：Logistic回归法＞支持向量机法=K最近邻法=灰色关联法＞Fisher判别法，即在本文中相比其余4种信用评价方法，Logistic回归法在适用范围上显示出优势。

3 结论

（1）本文将现有信用评价方法分为五类，分别为计量经济学方法、多元统计方法、人工智能方法、非参数方法以及数学优化方法，在每一类信用评价方法中选取一种高频研究方法，分别为：Logistic回归方法、Fisher判别方法、支持向量机方法、K最近邻方法以及灰色关联方法。使用这五种信用评价方法从判对率维度、软件操作维度以及适用范围维度进行优劣比较得到每个维度下的最优信用评价方法。

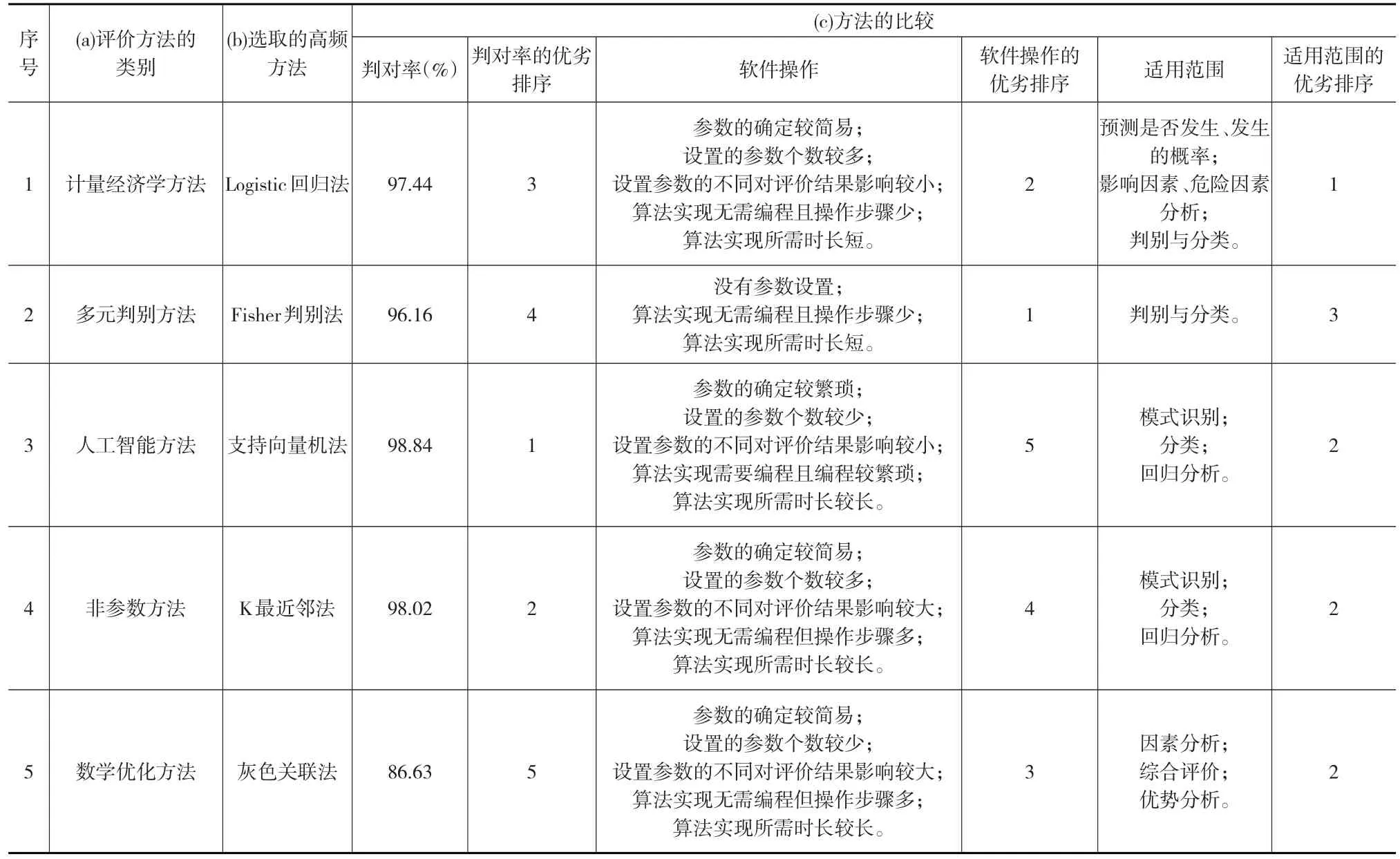
表12 信用评价方法的比较

（2）数据分析结果显示：判对率维度下信用评价方法有以下优劣排序：支持向量机法＞K最近邻法＞Logistic回归法＞Fisher判别法＞灰色关联法；软件操作维度下信用评价方法有以下优劣排序：Fisher判别法＞Logistic回归法＞灰色关联法＞K最近邻法＞支持向量机法；适用范围维度下信用评价方法有以下优劣排序：Logistic回归法＞支持向量机法=K最近邻法=灰色关联法＞Fisher判别法。所以，判对率维度下支持向量机方法最优，软件操作维度下Fisher判别方法最优，适用范围维度下Logistic回归方法最优。