点到直线距离公式的螺旋式推导*
●
(上海南汇中学,上海 201399)
利用代数的方法解决几何问题是解析几何的基本思想.通过对直线与二元一次方程的关系的分析,初步认识直线与方程的关系,从中认识向量知识的应用和坐标法的含义.《上海市中小学数学课程标准》明确提出让学生经历探求点到直线的距离公式的过程,掌握点到直线的距离公式[1].作为解析几何学习中的重要载体,点到直线的距离公式的推导不仅需要向量的“密切配合”,也需要“数形结合”思想的“积极参与”,可是课后经常会听到学生直呼“利用向量推导公式想不到,太难啦”.笔者认为教师平铺直叙的公式推导固然可以解决问题,但是效果可想而知.前苏联教育家维果茨基认为学生的发展有两种水平:一种是学生的现有水平,指独立活动时所能达到的解决问题的水平;另一种是学生可能的发展水平,也就是通过教学所获得的潜力,两者之间的差异就是最近发展区[2].教学应着眼于学生的最近发展区,为学生提供带有难度的内容,调动学生的积极性,发挥其潜能,超越其最近发展区而达到下一发展阶段的水平,然后在此基础上进行下一个发展区的发展.点到直线的距离公式推导中如何找准学生的最近发展区非常重要,利用学生两种水平之间的差异实现学生学习研究的螺旋式上升非常关键.
将“求解点P(1,1)到直线l:2x-y+2=0的距离”这种具体问题作为引入,由于其简单易操作,再加上课时紧张,很多教师会“忍痛割爱”,殊不知就是如此简单的问题就是至关重要的“台阶”,轻松帮助学生“拾级而上”,在熟悉的问题和方法引领下实现螺旋式成长的目标.
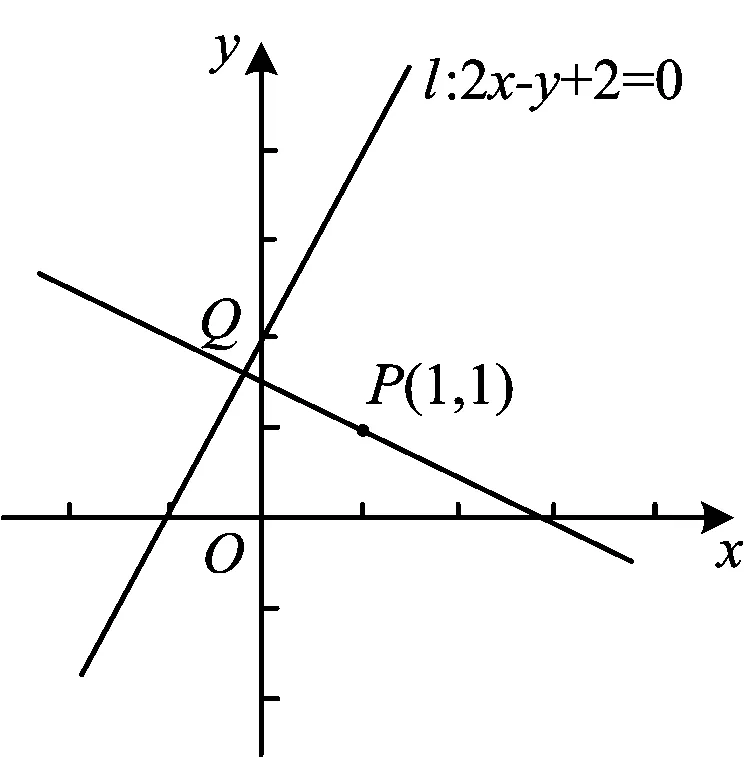
图1
分析1(定义法找垂足)直线外一点到这条直线的垂线段的长度叫点到直线的距离.根据定义学生马上考虑到点P和它在直线l的垂足Q的距离就是点到直线的距离,求垂足就是首选.
解法1如图1,过点P(1,1)与直线l垂直的直线方程为x+2y-3=0,联立方程组
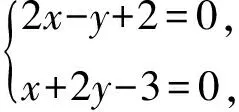
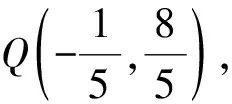
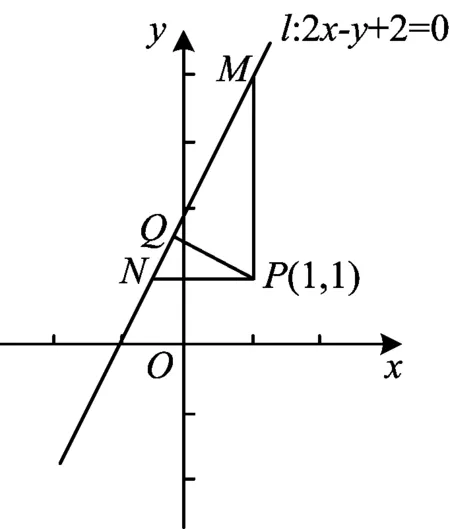
图2
分析2(几何法算面积)考虑到点到直线距离存在垂直关系,学生容易联想到高,既然有高就会考虑面积,那么如何构造三角形求面积呢?构造怎样的三角形比较容易操作?构造直角三角形是首选.
解法2如图2,过点P(1,1)分别作与x轴、y
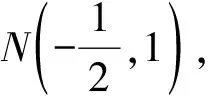
过点P作直线l的垂线,垂足为Q,设d=|PQ|,利用等面积得到
则
故
分析3(函数法求最值)分析点到直线的距离的定义,结合几何特征不难发现:点P到直线l上任意一点的距离的最小值就是点P到直线l的距离,于是将点P到直线l上任意一点的距离表示成某个变量的函数,利用函数求最值即可得到所求距离.
解法3在直线l上任取点M(x,y),满足y=2x+2,从而
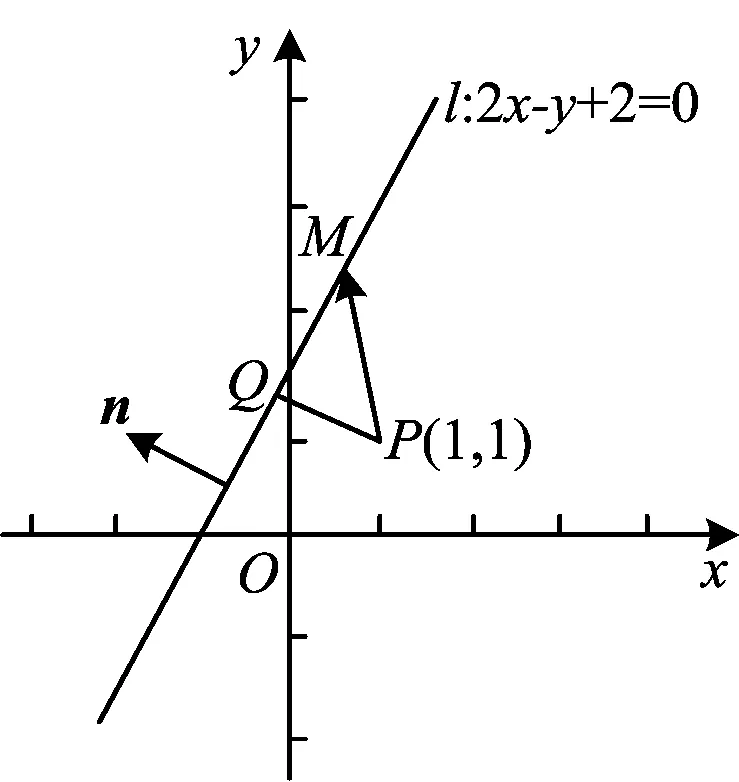
图3
分析4(向量法寻射影)既然可以利用直线l上任意一点M与点P距离的最值使问题得解,不妨大胆假设若点P,M确定,那么点P到直线l的距离也可以确定.
解法4如图3,在直线l上任取点M,过点P引直线l的垂线,垂足为Q.在Rt△PQM中,
d=|PQ|=|PM|·cos∠MPQ,
(1)
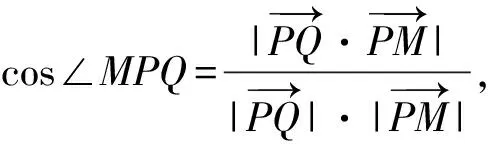
代入式(1),得
不妨取M(1,4),n=(2,-1),代入公式得到
从一个具体问题出发利用几种常见的方法使问题全方位解决,形成问题解决的方法链,经过教师适当总结提炼,此时将问题一般化就显得顺理成章.
研究点P(x0,y0)到直线l:ax+by+c=0(其中a,b不全为0)的距离,按照学生的思维习惯,很多学生会沿用具体问题的方法解决一般化问题.
学生从已有水平出发,将问题进行了从特殊到一般的推广,面对多个字母、繁杂运算等情况的出现,传统方法的使用遇到了困难,有些方法坚持一下还可以解决,有些根本难以继续,那么选择哪种方法解决比较简单、比较容易操作呢?有了前面基础的铺垫,找到学生可持续发展的能力水平,学生经过自我比较斟酌,认为向量法比较合适.虽然在具体问题解决中向量法并不占优势,但是在点到直线的距离公式的推导过程中,该方法不仅具有一般性,而且推导过程非常简便.教师针对学生的具体情况选择不同的教学方式和策略,并花时间让学生体验知识方法形成的完整历程,从短时效益考虑可能会影响一定的教学进度,但是就长远意义而言将会产生巨大的影响.找准学生的最近发展区,让学生体验学习发展的全过程,实现螺旋式发展的目标,为今后发现问题、分析问题、解决问题提供了可操作的途径和方法.

