一道几何题引出的关于辅助线教学的思考*
●
(湖州市第五中学教育集团余家漾校区,浙江 湖州 313000)
1 问题再现
题目如图1,在△ABC中,AD平分∠BAC交BC于点D,BC的中点为M,ME∥AD,交BA的延长线于点E,交AC于点F,
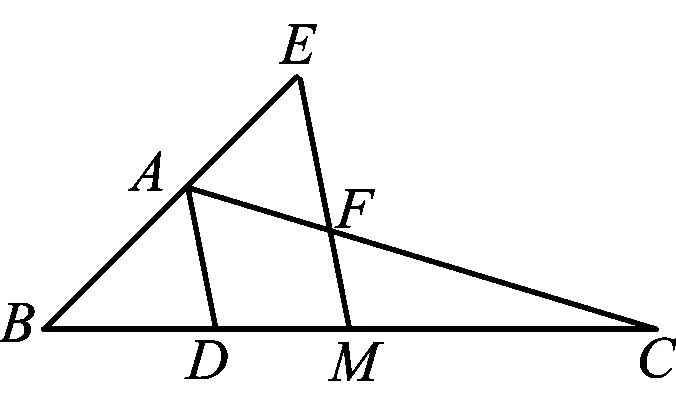
图1
求证:
1)AE=AF;
(2016年山东省淄博市数学中考试题第22题)
2 学生的解题状况及分析
2.1 解题状况
此题为中位线一课专题练习中出现的问题.批阅后笔者对所任教的两个班108位学生的解答情况作了简要统计,结果表明:大多学生能够解决第1)小题,但第2)小题仅有24人做对(其中选择倍长BE至点G,联结CG的有12人;选择作AB的中点G,联结GM的有7人;有2人选择了作CG∥BE,交EM延长线于点G;另外3人想出了其他方法).做错的学生中,过点C作EM平行线的共有22人,不得法的有5人.还有57人空题未作答.
2.2 错因分析
中位线的概念虽然与三角形有关,但教材之所以未将之放入三角形的相关章节,是因为其定理证明涉及平行四边形的性质和判定,于是将之安排到平行四边形一章的章末.
此题出现在中位线专题练习“与中点有关的辅助线作法”中.一方面,由于初学中位线定义,许多学生对于中位线定理的运用尚处于给图才能识别的阶段,主动构造中位线来解题的经验尚浅;另一方面,在三角形全等的相关学习中,学生已经接触过“倍长中线”的方法,但由于学习时间久远,基本功不扎实的学生难免遗忘.这都是造成学生空题的原因.
值得注意的是:有22人选择了过点C作CG∥EM,并直接认为EM是△BCG的中位线.但由于八年级学生并未学习过平行截割定理,因此,本题在目前阶段,利用这样的方式来添加辅助线并进行证明就有解法超前之嫌.事后笔者追问原因后得知:一小部分学生承认是通过课外辅导或查询网络的,其余大部分则是因为主观臆断了“中位线判定定理”(即过一边中点作另一边的平行线段,交第三边于一点,联结此两点的线段就是该三角形的中位线)存在而造成的.下面我们着重分析第2)小题的证法以及它们是怎样被想到的.
3 证法探究
由中点联想中位线,构造中位线,利用中位线定理解决问题是较容易想到的方法.
证法1如图2,延长BE至点G,使BE=EG,联结GC,则EM是△BCG的中位线,从而
EM∥CG.
由第1)小题知
∠AEF=∠AFE,
从而
∠G=∠ACG,
即
AG=AC,

图2 图3
证法2如图3,延长CF至点G,使CF=FG,联结GB,则FM是△BCG的中位线,故EM∥BG,从而
∠G=∠AFE, ∠GBA=∠E.
由第1)小题知
∠E=∠AFE,
即
∠G=∠GBA,
从而
AG=AB,
证法3如图4,取AB的中点G,联结GM,则GM是△BAC的中位线,GM从而
∠GME=∠AFE.
由第1)小题知
∠E=∠GME,
从而
GM=GE,
故
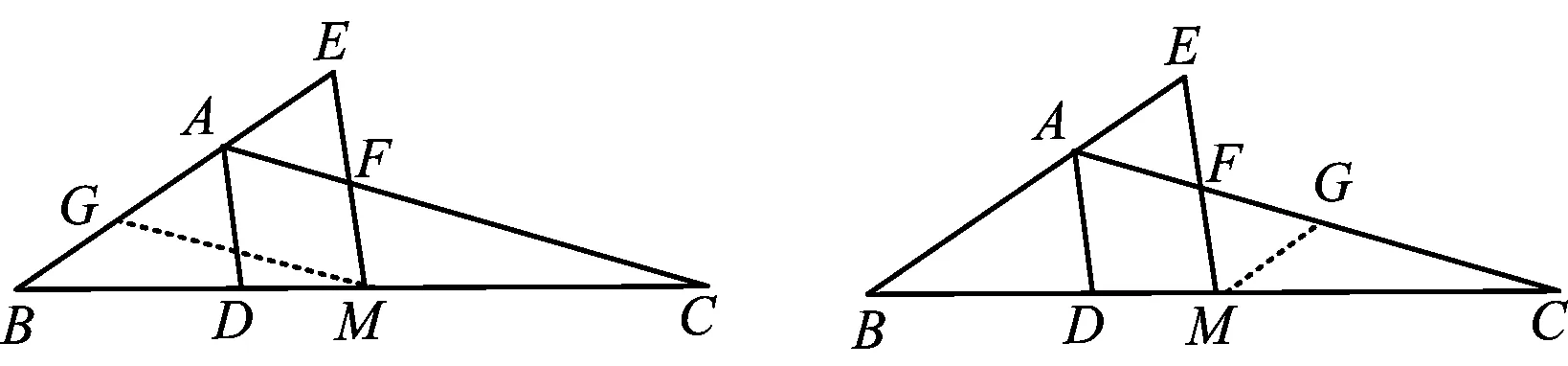
图4 图5
证法4如图5,取AC的中点G,联结MG,则MG是△BAC的中位线,GM从而
∠E=∠GMF.
由第1)小题知
∠GFM=∠GMF,
从而
GM=GF.
设GM=x,AF=y,则
CG=AG=x+y,AB=2GM=2x,AE=x,
于是
BE=AB+AE=2x+y,
AB+AC=2x+x+y+x+y=4x+2y=2(2x+y),
即
由中点不仅可以联想中位线定理,还可以用“倍长中线”法来构造全等三角形.

图6 图7
证法5如图6,倍长EM至点G,联结CG,则
△BME≌△CMG(SAS),
于是
∠E=∠G=∠CFG,
从而
CF=CG,
证法6如图7,倍长FM至点G,联结BG,则
△BMG≌△CMF(SAS),
从而
BGCF,
于是
∠G=∠AFE=∠E,
故
BE=BG,
因此
遗憾的是上述6种证法,大多数学生只想到了证法1和证法3,值得惊喜的是个别学生还想到了以下独到的证法.

图8
证法7如图8,分别取AB,AC的中点G,H,联结MG,MH,则MH,MG都是△ABC的中位线,易证
从而
评注此法充分利用了三角形的中位线定理,较之证法3和证法4,证法7看上去更为直观、易懂.但要想到它就不太容易,必须在平时的练习中做到精练多思.
证法8如图6,延长EM,以C为圆心、CF的长为半径画弧,交EM的延长线于点G,则结合第1)小题不难得知∠G=∠E,从而
△BME≌△CMG(AAS),
因此CG=BE,以下同证法5.
评注此法与证法5同图,但构造辅助线的方式大不相同,究其实质,也是在构造两个全等三角形.经过讨论,课后又有学生发现图6还可以解释为构造BE的平行线CG,同样可同证法5,可谓是“一图多法”了.若用同样的眼光去看待图7,那么证法6亦可衍生出类似于上述的两种方法,本文略.
由上可见,本题证法五花八门,梳理之后,我们发现这些证法之间既有区别又有联系.区别:其一,在于构造辅助线的外在表现形式(不同的辅助线添加方式)的差异;其二,构造辅助线的内在方法(即利用中位线、倍长中线、作平行线、等腰三角形作图等)的差异.但对于学生而言,更重要的是去思考如何发现这些证法之间的联系?不难发现在证法1~4和证法7中,点M是某一三角形中位线的一个端点;在证法5,6,8中,点M是某一对Z字型全等三角形的公共顶点.可见,无论哪种证法都是在围绕BC的中点M去构造辅助线的,可以说,这些辅助线方法的共同特征就是:它们都是由中点M所派生出来的图形.在解题中,学生若能抓住这一共同特性,那么上述各法就有可能接踵而来.
4 教学反思
4.1 在注重基本活动经验积累的同时加强逻辑推理的严密性
从解题的主要错误来看,误用中位线判定定理的学生占到81%.笔者注意到中位线一课的教学是从定义引入到定理证明最后到应用,在此过程中,笔者将主要精力投入到了定理证明的辅助线作法之中,而忽视了对于定义逻辑性基础的强调.与此同时,前期所学内容“定理与逆定理”、等腰三角形三线合一定理中的“知二推一”等的负迁移因素,也是造成学生误用“中位线判定定理”的一大诱因.可见,在平时的几何教学中,应当在注重基本活动经验积累的同时,要强调推理的严密性.对于一些存在逆定理的定理,如“30°角所对直角边等于斜边的一半”和“直角三角形斜边上的中线等于斜边的一半”等,应当在平时的教学中给出详细的逆定理的叙述和证明,切不可为了赶进度而“一语带过”.另一方面,在进行基本图形的教学过程中,亦应同时强调其逻辑性基础与使用前提,否则,学生可能出现张冠李戴的错误.
4.2 辅助线的学习应当呈“螺旋上升”之势
对基本技能的遗忘使更多学生选择了放弃,其中有部分学生未能想到辅助线的添法,但通过生生互动和讲解,大多数学生又恍然大悟,大有“为什么我没想到”之叹,辅助线对于他们来说,好比魔术师帽子里突然冒出的兔子一样不可思议.由此可见,“辅助线作法怎么教”成了几何教学的一大困扰.
在小学阶段,大多数几何定理都无法给出证明,如“三角形内角和定理”只是通过剪、拼、凑的实验方式向学生解释其正确性.这种实验式的操作活动为初中阶段对这个定理的辅助线证明埋下了种子.为此,教师应当在课堂上将学生的思维引导到如何借助小学的实验方法去发现这条辅助线上来,这样,思维的种子就有了发芽的可能性,辅助线的添加就水到渠成,这为学生更好地学习如何添加辅助线提供了一个重要范式.毫不夸张地说,许多学生正是从这一节课开始,对于辅助线添加的方法产生了浓厚且持久的兴趣,踏入到一座真正的几何花园中.
由此可见,对辅助线添法的学习应当是层层深入和螺旋式上升的,要经历一段漫长、深入的过程.初一学生接触线段的中点时就要经历从形到数或从数到形的表征与认识,这时,教师需要注重学生对数量关系(倍半等)的几何表述与理解.当学到角平分线内容时,这种数量关系的表征形式会自动从中点数量关系的表征形式中迁移过来,只不过对象从点变成了射线、线段变成了角,笔者认为这是“由点生形”的第一阶段.到了初二阶段学习了三角形的中线、全等三角形、等腰三角形等内容,开始学习“倍长中线”“三线合一”等技巧,此时,前一阶段关于线段的中点的表征内容又成为现阶段研究对象的常识,这是“由点生形”的第二阶段.学到中位线定理时,大多数学生已经开始明白前一阶段所学到的辅助线作法(倍长中线、见中点连中线等)都是在围绕中点开展的,初步具备了利用已知条件中的中点尝试作出辅助线的能力,这时,过去的倍长中线、见中点连中线等作辅助线的方法自然应成为现阶段学习内容中的常识(遗憾的是,那些空题的学生大多没有形成这一常识),如此学生自然会去思考如“见中点构中位线”的辅助线方法是否可行?这就是“由点生形”的第三阶段了.可以预想,到九年级学习相似三角形时,“由点生形”的点又可以拓展为非中点的情形,此时从第三阶段学来的那些思想方法又成为这一阶段的常识.笔者以为,“由点生形”的辅助线学习就是这样螺旋上升的.
反思学生解答的行为不难发现,空题的学生的主要问题出在“由点生形”的中级阶段.学习层次上出现脱节现象,就不难解释他们的束手无策了.弗赖登塔尔认为:常识要成为数学,必须经过提炼和组织,而凝聚成一定的法则.这些法则在高一层次里又成为常识,再一次被提炼组织凝聚成新法则,如此不断螺旋上升.数学的发展过程就显出层次性,构成许多等级.一个人在数学上达到怎样的层次因人而异,决定于他的先天和后天,但一个为多数人都能达到的层次必然存在.教师的任务就是去帮助多数人达到这一层次,并努力提高[1].

