基于逻辑推理数学核心素养培养模式的尝试*——以“对棱相等四面体的由来”为例

●

(镇海中学,浙江 宁波 315200)

1 教学内容与核心素养分析

1.1 地位和作用

对棱相等四面体是一类特殊的四面体，它可以通过截取长方体得到，也可以将对棱相等的四面体补形成长方体.那么为什么对棱相等的四面体能补形成长方体？对如何补形、为何补形的思考可以促进学生逻辑推理能力的提升.

1.2 核心素养分析

逻辑推理是从一些事实和命题出发，依据逻辑规则推出其他命题的思维过程[1]，从折纸游戏中直观感知对棱相等四面体的4个面都是锐角三角形，进而思考：为什么不能是直角三角形和钝角三角形，是不是任何一个对棱相等的四面体都可以补形成长方体，有没有可能存在一个四面体满足对棱相等的条件但不能补形成长方体，为什么可以借助最小角定理帮助理解对棱相等四面体补形成长方体？

2 教学目标和目标解析

教学目标折纸游戏中直观感知对棱相等四面体的4个面是全等的锐角三角形，在对对棱相等四面体补形原因的思考过程和证明过程中培养了逻辑推理这一数学核心素养.

目标解析在长方体中可以截得对棱相等的四面体，相反对棱相等的四面体可以补形成长方体，从正反两方面对对棱相等四面体进行思考，在思考过程中形成对其全面深入的认识.结合动手操作从折纸游戏中获得直观认识，认识到对棱相等四面体的4个面是全等的锐角三角形，并在借助最小角定理证明对棱相等四面体能补形成长方体的过程中培养学生的逻辑推理能力，即在教学中有意识地培养学生的逻辑推理能力，拓展数学思维，提升数学品质.

3 教学问题诊断分析

长方体可以截得对棱相等的四面体，而对棱相等的四面体为什么能补形成长方体，学生可能只是被动地接受而没有主动地思考过这一问题.让学生对问题进行多角度的认识，进而对对棱相等四面体有更深入的认识，在对对棱相等四面体补形成长方体这一熟悉问题的重新提出、思考、解决的过程中，培养了学生的逻辑推理这一核心素养.

4 教学过程设计

角度1折纸剪纸游戏，直观感知对棱相等四面体的形成过程和图形特征.

游戏1如图1，请分别沿锐角、钝角、直角△ABC的3条中位线DE，EF，DF进行翻折，翻折过程中点A，B，C能重合吗？

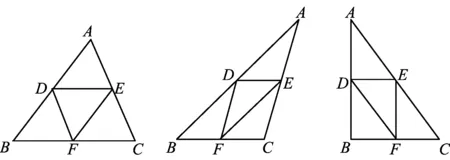
图1

生1：只有翻折锐角△ABC时，点A，B，C才有可能重合.

师：为什么只有在锐角三角形时，才有可能重合呢？请大家思考沿DE翻折△ADE时，点A在底面DEF的投影的运动轨迹是什么？

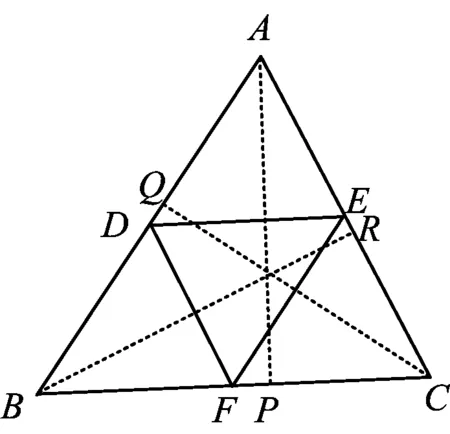
图2

生2：如图2，过点A作DE的垂线，交BC于点P，点A在底面上的投影的运动轨迹为垂线段AP.

师：同理沿DF翻折△BDF时，点B在底面DEF上的投影的运动轨迹为垂线段BR,沿EF翻折△EFC时，点C在底面DEF上的投影的运动轨迹为垂线段CQ.锐角三角形的3条垂线段交于同一点，而钝角三角形的3条垂线段交于三角形外一点，直角三角形的3条垂线段的交点为直角顶点B，因此只有沿锐角三角形的3条中位线进行翻折时，点A，B，C才有可能交于同一点.

师：当点A，B，C重合时，不妨记为点S，如图3，此时四面体S-DEF的对棱长度之间有关系吗？

师：锐角三角形沿3条中位线翻折的过程中可以得到一个对棱相等的四面体.

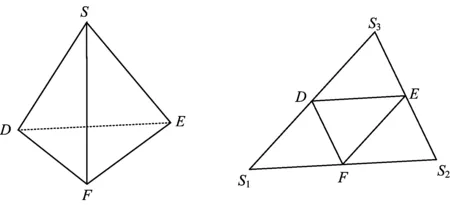
图3 图4

游戏2如图4，将对棱相等的四面体S-DEF分别沿SD,SE,SF剪开展平，使△S1DF，△S2EF，△S3DE与△DEF共面.

师：四面体S-DEF的对棱相等，则

△S1DF≌△S2EF≌△S3DE≌△DEF，

从而

∠EDF=∠S3ED, ∠S1DF=∠DS3E,

于是 ∠S3DE+ ∠EDF+∠S1DF=

∠S3DE+∠S3ED+∠DS3E=π,

即点S3,D,S1共线，同理点S2,E,S3共线，点S1,F,S2共线.也就是说对棱相等的四面体展开后是一个三角形，将这个三角形沿3条中位线进行翻折就还原回了原来对棱相等的四面体，即说明△S1S2S3是锐角三角形.

生4：原来对棱相等四面体的每个面都是锐角三角形.

设计意图学生从折纸游戏中直观感知对棱相等四面体的4个面是全等的锐角三角形，为对棱相等四面体能补形成长方体这一问题的提出和解决作好铺垫.

角度2最小角定理助推解释补形.

生：对棱相等的四面体能不能补形成长方体的关键是看这个长方体能不能找到.假设能找到，设对棱相等四面体S-DEF的对棱长分别为u，v，w，补形后的长方体的棱长分别为a，b，c，则长方体的棱长分别为

只需说明

u2+v2>w2,u2+w2>v2,w2+v2>u2，

进而说明a,b,c是可以取到的.

图5

如图5，作SH⊥平面DEF于点H，由cos∠SDE=cos∠SDH·cos∠EDH，得

∠SDE>∠EDH,

同理可得∠SDF>∠FDH，从而

∠SDE+∠SDF>∠EDH+∠FDH=∠EDF,

于是

∠SDE+∠DSE>∠SED，

同理可得

∠SDE+∠SED>∠DSE,

∠DSE+∠SED>∠SDE，

即△SDE中任意两角之和大于第三个角，亦即△SDE为锐角三角形，也就说明u2+v2>w2，u2+w2>v2，w2+v2>u2是成立的，可以将对棱相等的四面体补形成长方体，进而在长方体中研究解决问题.

设计意图借助最小角定理解释对棱相等四面体的4个面是全等的锐角三角形，说明了补形的原因，同时有助于培养学生的逻辑推理素养.

角度3[2]对棱相等四面体可以补形成长方体，体会在长方体中研究四面体性质的优越性.

师：接下来我们就来研究对棱相等四面体的性质.

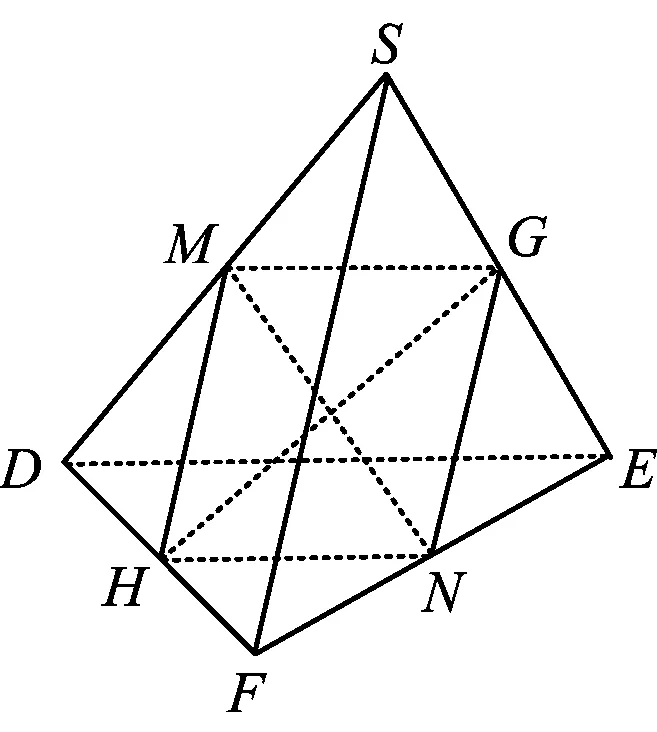
图6

性质1对棱相等四面体的对棱中点连线互相垂直.

如图6，设M,N，G,H分别为SD,EF,SE,DF的中点，可得四边形MHNG为菱形，从而NM⊥GH.

性质2[2]对棱相等四面体的外接球球心与内切球球心重合.

因为对棱相等的四面体可以补形成为长方体，所以它的外接球球心即为补形后的长方体的中心.不妨设为点O，由|OS|=|OD|=|OF|=|OE|,知4个小四面体O-SDE，O-SDF，O-SEF，O-DEF全等，从而点O到平面SDE、平面SDF、平面DEF、平面SEF的距离相等，于是点O也为这个四面体内切球的球心.

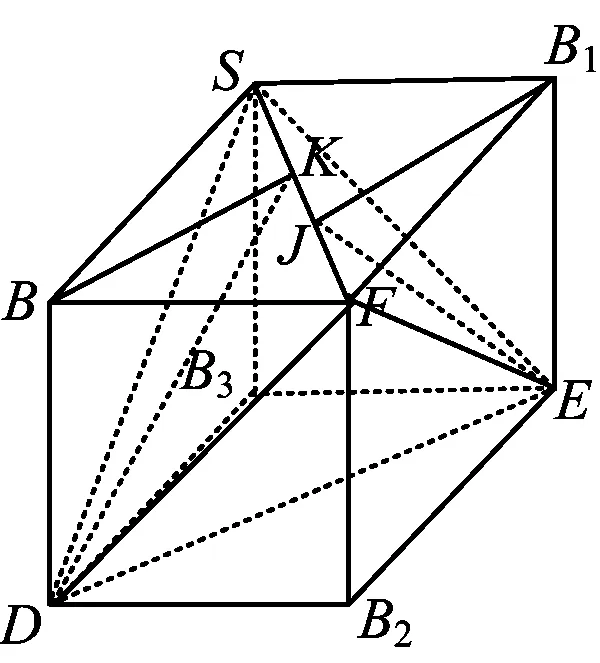
图7

性质3对棱相等四面体的任意3个面与第4个面所成角的余弦值之和为1.

由于对棱相等四面体可以补形成长方体.如图7，作BK⊥SF于点K,B1J⊥SF于点J，联结DK，EJ，则平面DSF与平面SFE所成角α的大小为π-∠BKD-∠B1JE，从而

cosα= cos(π-∠BKD-∠B1JE)=

-cos 2∠BKD=-(2cos2∠BKD-1)=

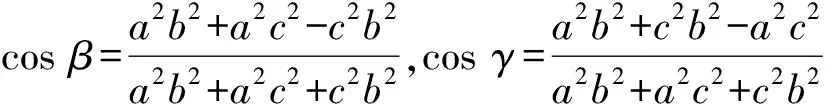
cosα+cosβ+cosγ=1.

波利亚曾说：“一个有责任心的教师与其应付繁琐的教学内容和过量的题目，还不如选择一个有意义但又不复杂的题目去帮助学生深入挖掘题目的各个侧面，在指导学生解题的过程中，提高他们的才智和推理能力.”以学生的疑惑为出发点，对对棱相等四面体的由来有一个更深入的认识，在“为什么补形、怎么补形、如何在补形后的图形中研究性质”等一系列问题的研究中，培养学生的逻辑推理素养.