合理创设问题情境 发展数学核心素养*
——余弦定理的教学案例设计
●
(南京市第二十九中学,江苏 南京 210036)
0 引言
《普通高中数学课程标准(2017年)》(以下简称《新课标》)的最大亮点就是以学科核心素养为主要抓手.数学核心素养包括:数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析等.如何培养和发展学生的数学核心素养成为当今高中数学课堂教学关注的热点.如何让数学核心素养的先进理念从学术领域走向课堂实践,笔者通过余弦定理的教学案例做了部分教学实录,以飨读者.
1 内容解读与目标设置
余弦定理位于苏教版《数学(必修5)》第1.2节,在此之前学生已经学习了三角函数、平面向量、正弦定理等相关知识,这为学习本节内容起到了很好的铺垫作用.本节课的教学重点是余弦定理的发现过程和公式的推导,教学难点是余弦定理的发现及证明.
2 学情分析与教学策略
本课之前,学生已经熟悉了三角函数、平面向量和正弦定理等内容,在此基础上利用几何法、向量法、解析法等探求余弦定理,学生已有一定的基础.由于学生的创造意识不强,分析问题不够深入,使得学生在余弦定理推导方法的探求上有一定的难度.另外,从具体问题中抽象出数学的本质、应用方程思想建构一般化数学模型以及解决数学形式化问题是学生的难点.突破的主要策略是:通过合理创设问题情境,引导学生积极思考,通过师生间交流、学生间相互合作,力求让学生自主探究出余弦定理的公式.学生经历定理产生的过程,认识到新旧知识之间的联系,在探究过程中不断感受解决数学新问题、构建数学新知识的方法,从而切实增强自身的数学核心素养.
3 教学情境设计与思考
3.1 知识回顾,温故知新
师:1)正弦定理是三角形的边与角的等量关系,正弦定理的内容是什么?你能用文字语言、数学语言叙述吗?你能用哪些方法证明呢?
生1:正弦定理:在一个三角形中各边和它的对边的正弦比相等,即
其中2R为三角形外接圆的直径.
师:2)运用正弦定理可以解决哪些解三角形问题呢?
生2:可以解决两类问题:一类是已知两角及其一边解三角形;另一类是已知两边及其一边的对角解三角形.
设计意图问题的呈现基于旧知识的复习,也强化数学定理的应用,具有可操作性.在数学知识的建构中,注重整体认知,在知识的发生过程中,找到新知识的“生长点”,构建起解三角形的整体框架,从而有利于发展学生的数学抽象、逻辑推理和迁移能力等方面的核心素养.
3.2 创设情境,提出问题
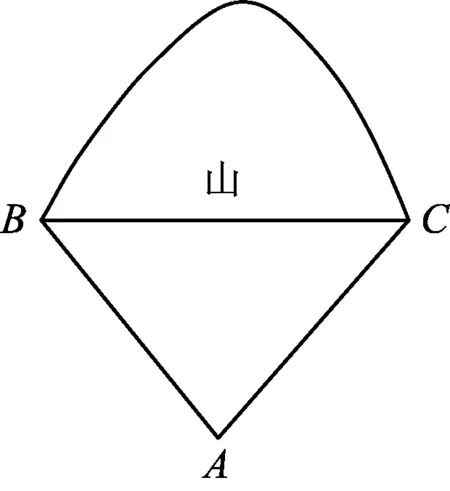
图1
例1某铁路工程队路线规划要经过一座小山丘,就需要挖隧道.挖隧道就涉及到一个问题,就是要测量出山脚的长度.而两山脚之间的距离是没有办法直接测量的,那要怎样才能知道山脚的长度呢?工程技术人员先在地面上选一适当位置A,量出A到山脚B,C的距离,再利用经纬仪测出A对山脚B,C的张角,最后通过计算求出山脚的长度BC.若测得AB=3 km,AC=4 km,张角A=60°,则BC=______.
设计意图数学来源于生活,激发学生应用数学的兴趣,通过背景材料的解读,引入探索性的思考.
师:能否把这个问题抽象成一个数学问题?
生3:问题转化为“在△ABC中,已知AB=3 km,AC=4 km,∠A=60°,求边长BC.”这其实是一个已知三角形的两边与夹角,求第三边的问题.
师:本题能否用最近所学的“正弦定理”求解?
设计意图合理创设问题情境:激活学生的已有经验,自然联系,产生新知,培养逻辑推理、数学抽象等数学核心素养.
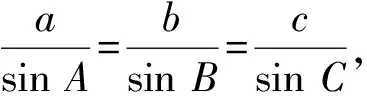
又B+C=120°,可得
即
分析知cosB≠0,从而
进一步可求出
点评本例利用正弦定理及三角函数方程能顺利求解,但此法往往在日常教学中会被师生轻易否定,寻求其他方法,可能是畏难,亦或是不利于推出余弦定理的形式.
《新课标》指出:“高中阶段至少应安排一次较为完善的数学探究、数学建模活动.”课堂教学要突出效率,而科学探究是一个长期的、艰难的、反复的探索过程.如果要在一节课的时间里经历整个过程,反而探而不究,或者探究比较肤浅,流于形式,那么学生能力得不到真正提高.在探究体验过程中,教师要摆正自己的位置,把自身角色定位于学生的合作者、鼓励者、引导者,从特殊到一般,从直观到严谨,有助于学生把所接触的问题逐步上升到理性的过程[1].
师:几何问题可以用几何解法吗?
设计意图合理创设问题情境:用“几何法”解决几何问题天经地义,借助几何直观和空间想象感知事物的形态与变化,利用图形理解和解决数学问题,培养学生直观想象的数学核心素养[2].
生6:可以构造直角三角形,借助“几何法”中的勾股定理求解.
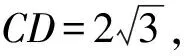
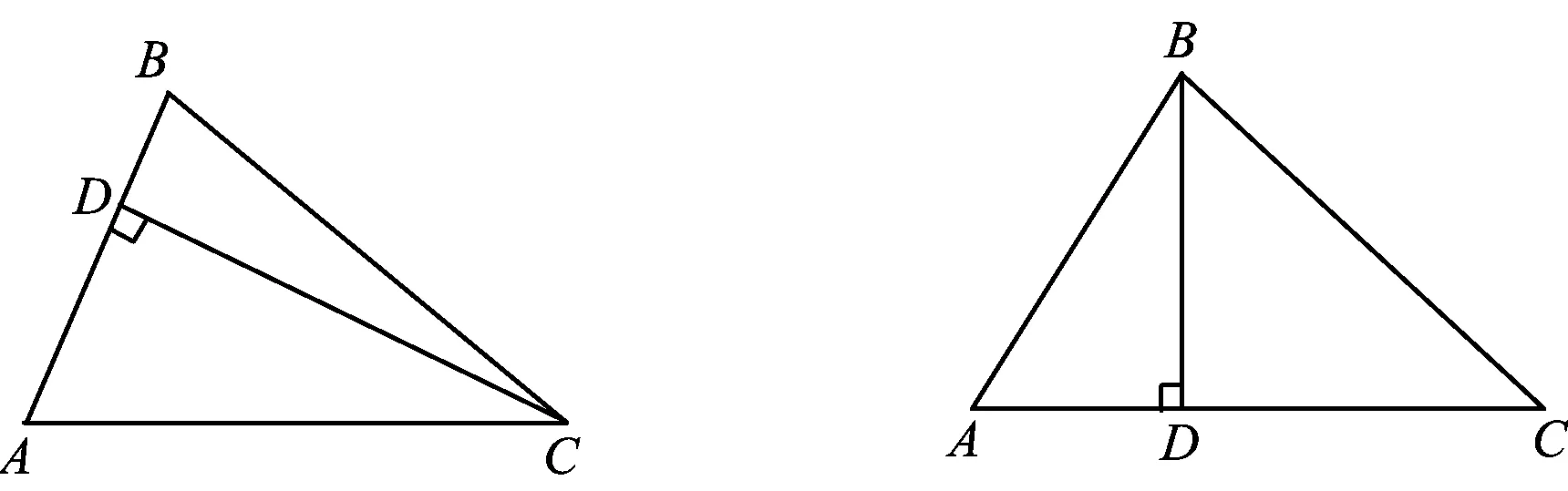
图2 图3
生7:如图3,若作BD⊥AC,D为垂足,则可仿生6同样求解,过程略.

图4
生8:如图4,若作AD⊥BC,D为垂足,虽然会遇到一些麻烦,但是经过一番思考运算仍可求解.为表述方便,不妨令AB=c,AC=b,BC=a,∠BAD=∠1,∠CAD=∠2,则
a2=(BD+CD)2=BD2+CD2+2BD·CD=
c2-AD2+b2-AD2+2bcsin∠1·sin∠2=
b2+c2-2bccos∠1·cos∠2+2bcsin∠1·sin∠2=
b2+c2-2bccos(∠1+∠2)=b2+c2-2bccosA,
代入已知数据即可得到例1的解答.
点评3名学生的解法都很好.生8的解法看似最难求解,但通过一般化的探索能得出整齐优美的数学表达式,即为我们今天要学习的“余弦定理”的一般形式,很是难得.探究活动中有很多教师预想不到的问题出现,课堂的不可控性远大于传统课堂.新课程之所以提倡积极主动的探究学习方式,目的是为了丰富、改进学生的学习方式,发挥学生的主动性.在教师指导下逐步提升逻辑推理、数学运算、数学抽象等核心素养.
师:本题能否用“向量法”求解?
设计意图合理创设问题情境:利用“向量法”解决几何问题.苏教版《数学(必修4)》在三角函数、平面向量等章节已经逐渐渗透运用向量方法来解决几何问题,用向量的符号语言描述几何问题,引入向量的运算来解决几何问题,从实际背景中抽象出一般规律和结构,学生应该有所了解.逻辑推理是从已经总结出来的规律中推出新的规律,这是数学生长和发展的主要途径,借此培养学生的逻辑推理、数学抽象等核心素养.
b2+c2-2bccosA,
代入已知数据很快可得到解答.

即
a2=abcosC-cacos(π-B),
得
a=bcosC+ccosB,
变形为
a-bcosC=ccosB,
两边平方得
a2-2abcosC+b2cos2C=c2cos2B,
即a2-2abcosC+b2(1-sin2C)=c2(1-sin2B),
而由正弦定理得bsinC=csinB,也可得到
a2=b2+c2-2bccosA.
点评殊途同归,生9通过两边平方让向量问题数量化能很快求得结果,而生10的运算也是合理的,理应得到积极评价与尊重,完成了从射影定理“a=bcosC+ccosB”到与余弦定理的跨越,展示了高超的运算水平,也体现了数学的探究过程并非一帆风顺.另外,注意到生8~10得到了同样优美的代数形式,余弦定理的一般化形式呼之欲出.
师:本题能否用“解析法”求解?
设计意图合理创设问题情境:几何问题代数化.在坐标系下用“解析法”处理几何问题是重要而且有效的途径,体现了数学建模的核心素养.数学建模是应用数学解决实际问题的基本手段,也是推动数学发展的动力.通过数学建模对现实问题进行数学抽象,用数学语言表达问题,最终解决实际问题.

图5
生11:建立如图5所示的平面直角坐标系,A(0,0),C(4,0),B(3cos 60°,3sin 60°),D(3cos 60°,0),在Rt△BCD中,由a2=BD2+CD2很快就可以算得结果.
点评以上问题情境的创设,都是贴近学生的认知基础,依托学生的“最近发展区”提出来的.教师做好宏观调控,让学生的探究有明确的目标和方向,探究过程有亲切感和获得感,对于余弦定理公式的推导和发现也是水到渠成、顺理成章.但如果将课堂全部交给学生自由发挥,或者直接由教师代替学生选择某种方案,即很快推出余弦定理,这样的课堂可能会无序或单调,学生有活动无体验,有经历无感悟,达不到探究的效果.通过这样多方位、多角度的探究活动,让学生的认知水平、运算能力得以落实,将所学知识融会贯通,迁移能力不断提高,在探究活动过程中学生也会体验到从数学规律中发现的愉悦和成就,数学核心素养的若干方面自然得以培养和发展.
3.3 建构数学,归纳概括
一般化在△ABC中,已知AB=c,AC=b,求∠A,a(即BC).
师:如何把例1一般化与形式化?
生12:从上面例1的解决方案中,利用几何法、向量法及坐标法均可由特殊到一般地将本问题解决好,立即得到
a2=b2+c2-2bccosA,
此为“余弦定理”的形式之一.其中几何法中要讨论三角形的形状,考虑锐角、直角、钝角在作辅助线垂线时对图形的影响.
点评要让学生在对“引例求解”体验的建构中生成真正属于自己的数学核心素养.数学核心素养的发展不能仅仅通过教师的“教”而获得,它更离不开学生的亲自体验.教师可以引导学生从特殊到一般,不断拓展解题思路,最后得出数学的重要结论.
4 评价与反思
教师的“教”不仅要让学生“学会”,更重要的是要让学生“会学”.在本节课的教学中通过创设合理的问题情境,充分调动学生已有的认知结构,让学生经历从“现实问题转化为数学问题,从已知不断探求新知”的过程,让学生充分参与进来,主动探索,发现新的知识,感悟新知识的形成过程,从而进一步完善自身的数学知识结构.数学教学提倡深度学习,教师通过了解学生、依据学情、创设问题情境,原创性地设计教学,在课堂上引领学生进行更多地思考与探索,提高师生互动、生生互动的质量,促进学生的理解、创新、发现.数学核心素养中数学抽象、逻辑推理、数学建模、直观想象、数学运算等方面在学生深度参与后才能有效构建[3].

