初中数学教学中提问设计的思考
刘 勇
(江苏省南通市实验中学 226001)
一、设计引入环节中的提问
案例1:“近似数与有效数字”的新课导入设计
资料1:李宇春、周笔畅、张靓颖是“超级女声”选秀比赛中胜出的前三名歌手,她们当时获得的支持短信数分别为3528308、3270840、1353906.2012年播出的“中国好声音”火爆整个暑期,但这一节目却因为不公开选手实际得票数受到广大观众与网友的质疑.
资料2:英国妇女夏洛特·凯利4年中生了两次双胞胎,今年7月30日出生的露丝与艾米丽的体重分别约为8.12磅、7.20磅.
问题1:大家以为资料1与资料2在数据的表达上有区别吗?
(引导学生在数据的比较中发现数字的精确性与近似性,为课堂研究内容埋下伏笔)
问题2:大家以为“中国好声音”这一节目为什么会遭到广大观众与网友质疑呢?
问题3:资料2中双胞胎体重的描述为什么会用“约”这个词呢?这个词是否可以通过精确的测量将之省略呢?
(引导学生在两个问题的思考中明白近似数与精确数存在的意义与价值)
进一步提问:大家能否举出有关精确数与近似数的生活实例呢?
从学生感兴趣的话题引入课堂研究的主要内容,使学生积极性高涨并更加快速地进入学习状态.
二、设计探索环节中的提问
案例2:“勾股定理的应用”的探究问题设计
例题如图1,等边三角形ABC的边长为6,则△ABC的面积是多少呢?
作出△ABC一边上的高即可快速求得△ABC的面积.为了帮助学生更加灵活地掌握知识并实现知识的迁移,可以设计以下变式.

变式1:如图2,在△ABC中,AB=AC=17,BC=16,试求△ABC的面积.
问题背景:等边三角形变成等腰三角形是特殊到一般的过渡,这一微小的变化并不会难住学生,学生运用类似的解法很快即可解决这一问题,在此题的小结归纳中可设计以下提问:
问题1:大家认为例题和变式1的解答中存在相通的地方吗?具体的解题中都有哪些知识点被运用了呢?
(解题中都作了三角形一边上的高,等腰三角形的“三线合一”、勾股定理等相关知识在解题中得以运用)
问题2:根据例题可知,知道三角形的边长即能求出等边三角形的面积,那么,我们至少需要知道哪些条件才能求得等腰三角形的面积呢?
问题3:求三角形面积时,你还可以给出哪些条件呢?
问题4:假如把AB=AC=17这一条件换成△ABC周长为50,且AB=AC,再把BC=16换成底边上的高是15,该等腰三角形的面积应该怎么求呢?
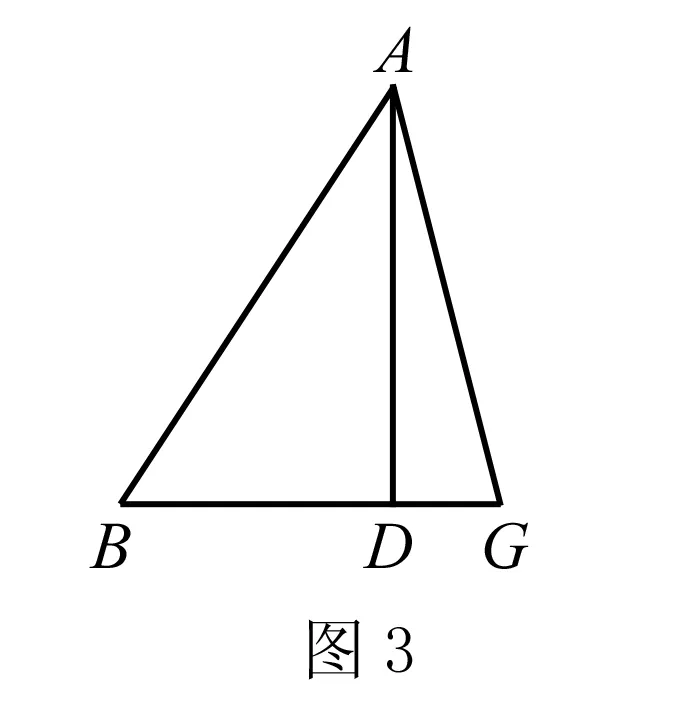
变式2:如图3,在△ABC中,AD⊥BC,AB=15,AD=12,AC=13,求△ABC的面积与周长.
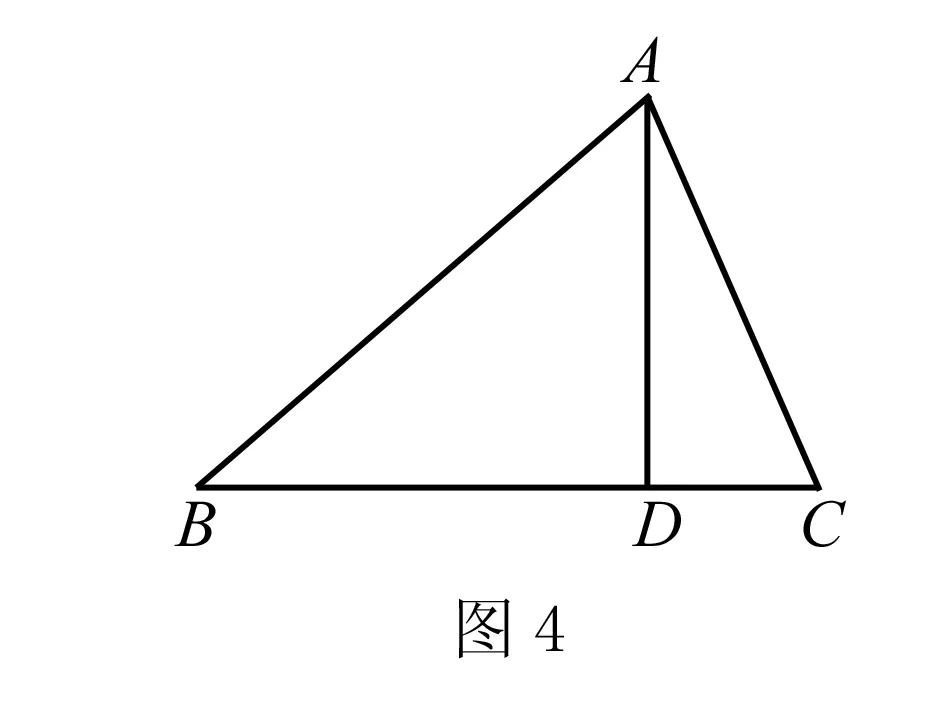
变式3:如图4,在△ABC中,AB=15,AD=12,BD=9,AC=13,试求△ABC的面积与周长.
变式4:已知S1、S2、S3分别是△ABC的边AB、BC、AC为直径的半圆的面积,且S2+S3=S1,请判断△ABC的形状.
上述一系列不断变换条件和结论的变式由浅入深、由特殊到一般,将勾股定理及其逆定理的性质运用进行了充分的融合,教师设计的环环相扣的一系列新问题也更好地锻炼了学生对勾股定理的理解与应用,学生的数学能力在利用“数形结合”与“转化”思想解决问题的过程中也得到了很好的锻炼与发展.
三、设计课堂小结环节中的提问
对数学知识进行概括归纳并使其系统化是归纳整理环节最为主要的任务,课堂教学中对知识点、数学思想与方法进行及时的归纳整理还能使学生的理解、记忆得到升华与发展,因此,教师在课堂教学的整理归纳环节所设计的提问应该是能够促进学生对所学内容的领悟与内化的,由此可见这一环节中提问设计的重要性.
案例3:“勾股定理的应用”的课堂整理
教师在这一内容的归纳整理中可以先提出具体的问题,然后再引导学生在具体问题中抽象出一般性的结论,使学生能够在教师的引导中归纳出本课研究内容中所涉及的数学思想.
问题1:大家知道勾股定理及其逆定理在应用上的区别都有哪些吗?(求解线段的长度、图形的面积与周长往往会运用到勾股定理,判断三角形的形状则会运用到勾股定理的逆定理)
问题2:通过本课的学习,大家能体会出哪些数学思想呢?请大家结合例题并进行举例说明.
(数形结合,转化等)
问题3:大家回顾自己的解题过程与思路,自己在解题中犯错了吗?,犯了哪些错误?有哪些是自己在今后解题中需要特别重视的?
一系列更具实效性的问题有效避免了空洞的说教,学生在逐个问题的思考与回答中也进一步明确了本课学习的重点,完成本课学习内容的归纳与小结之时,学生还在自己的有效回顾中进行了易错点的分析,这能使其对知识形成更好的理解与记忆.
教师在课堂教学的导入、探索以及归纳整理环节中所设计的有效问题能够帮助学生进行更深层次的思考,因此,教师不仅要注意问题设计的质量,还应把握提问的技巧并尽量有艺术性地将问题展现在学生面前.不仅如此,学生在课堂活动中展现出的情绪情感以及和谐民主课堂氛围的营造也是教师需要注意的,这能使师生之间的距离靠得更近,学生会因为教师的亲和力对课堂学习内容表现出更加积极的情绪.

