巧用数学工具 妙解物理问题

曹 华

(江苏省海门市六甲初级中学 226100)

物理问题中的很多问题可以用数学方法和数学工具来解决，而这类物理问题内在有一些共同的特点，以此向对应，这类数学方法或数学工具也有同样的特征，这类特征教师需要潜意识的帮助学生归类、讨论、分析、汇总、总结，那就是方法和思想上的提升.这不仅可以巧妙的达成物理问题的巧妙解决，更能将数学和物理学科的价值充分融合，达成美丽与智慧的共生.笔者借助下文几道经典题，谈谈方法上的变通与剖析，以此抛砖引玉.

一、常规方法温习

例题1 小明从A点出发到B点，前一半时间的速度是v1，后一半时间的速度是v2,求整个过程中的平均速度？

例题2 小明从A点出发到B点，前一半路程的速度是v1，后一半路程的速度是v2,求整个过程中的平均速度？

解决这两道似曾相识的题目，很多教师都遇到过，解决这道题目的难点也在于常规数学方法的应用，是学生应该掌握的一项基本数学技能，也是数学和物理灵活应用的一种要求.我们设第一题的平均速度为Vt，设总时间为2t，设第二题的平均速度为Vs，设总路程是2S具体如下：

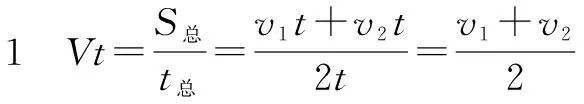
这两种方法将数学的计算和物理的情境相结合，通过计算让学生感受到数学计算方法在本题中的重要性和价值性.而这重要性和价值性也激发了学生对“数学工具解决物理问题”产生了浓厚的学习兴趣，以此促使学生在本环节的进一步深入和研究.

二、变通方法提升

为了进一步提升数学工具在物理问题中的价值，并进一步将物理问题进一步深化，一方面提升学生对物理问题的分析与解剖能力，另一方面借助物理问题的深入，提升数学工具在物理问题中的价值.

例题3 在例题1和2的基础上，请你判断整个过程中Vs和Vt的大小关系？

这一问题情境的解决策略很快转移到数学工具中来，为此，教师要启发学生用两种数学思想来解决.

方法1：特殊值代入法.学生将V1和V2设置成简单易算的特殊值代入Vs和Vt的等式时，Vs和Vt的值也就很快揭晓，而大小关系也就一目了然，特殊值代入法虽然从学术研究角度分析，有失学术研究的严谨性、科学性、严密性，但是从问题解决的角度分析，这未尝不是一种好的思想和方法，值得我们借鉴和应用.

无论学生采用哪种方法得出结论，也无论学生站在哪个角度去解决这个问题，学生在这一变式拓展的训练中再次感受到数学应用技能在物理学习中的重要性和价值性，也深刻体会到数学与物理之间的共融之处.

三、变式训练归类

为了真正促进学生学科关键能力的有效提升，促进学生在学习过程中达成减负高效的学习效果.我们的变式需要在常态变式的基础上锁定变式的方向和目标，方向我们不仅要在知识与技能的广度上进行变式，还要在思想与方法的深度上进行变式，广度是为了普及学生的知识面，达成学以致用的效果，而深度是从多个层面训练学生的学科素养，促进学生对问题解决灵活性、普及性，真正促进学生综合素养的提升.而学科素养和综合素养的提升，将直接全面而深刻的促进学生关键能力的提升.

变式1：密度为ρ1和ρ2的两种物质等体积混合后，密度为ρV，密度为ρ1和ρ2的两种物质等质量混合后，密度为ρm(混合后总体积为两体积之和.)，求出ρV和ρm的大小？试比较ρV和ρm的大小关系？

本题的变式是基于原有例题1、2、3的基础上呈现出来的，主要目的对于类似情境问题的判断和解析，判断，是能站在不同的知识与技能层面判断前后两种不同情境的相似之处，即被求解的物理公式都是比值类的，即V=s/t,ρ=m/v,而密度为ρ1和ρ2的两种物质等质量混合与前一半路程速度是V1，后一半路程速度是V2的数学类型是一样的.密度为ρ1和ρ2的两种物质等体积混合与前一半时间速度是V1，后一半时间速度是V2的数学类型也是一样的.在这种相似的情境下，让学生去判断，就提升了学生对物理情境和数学形式的辨析能力.而解析的过程即将数学的计算和判断再次进行同类训练，强化了学生对相应方法与技能的训练，促进学生相应类型的解析能力，提升了数学工具实用解题能力，也让学生在训练中自发的将这种类型的题目和方法归为一类.

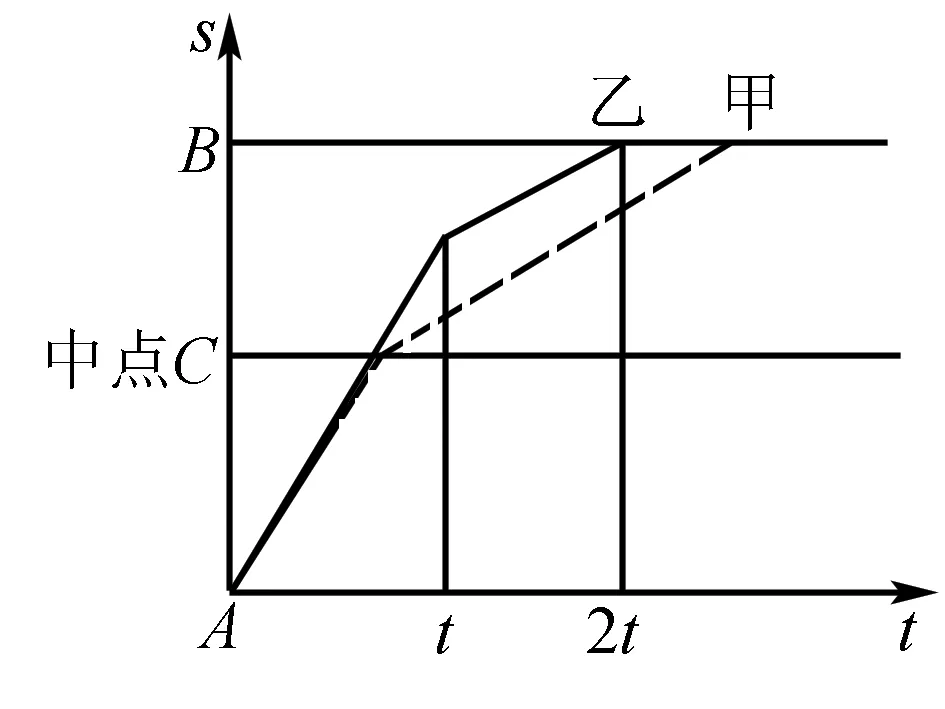
变式2：甲和乙共同从A点出发到B点，甲同学前一半路程的速度是V1，后一半路程的速度是V2,乙同学前一半时间的速度是V1，后一半时间的速度是V2，(V1>V2).请用S-t图像描述甲和乙两同学整个过程中的运动情况.

此处的变式将物理的具体情境用数学图像来描述，此时的难度和广度都上升至很高的层面，具体可以从三个层面达成理解和突破，答案如图所示.

1.大小的比较.学生需要在原有的理解基础上得出Vs

2.共走的判断.学生需要分析甲乙两人在整个运动过程中共同走过的区域，这个区域判断出来也就清楚分开走过的区域.即一开始走过的路程是共同完成的，而除此之外，就是分开运动的，且由于运动相似之处，即运动图像是平行的.

3.拐点的锁定.随着前一半时间和前一半路程的完成，将会出现新的拐点，由于V1>V2，所以前一半时间走完的路程将大于总路程的一半.因此，当甲同学走完一半路程后，将以V2的速度运动时，乙同学讲继续以V1的速度前进.而此时将出现第一个拐点，而等乙同学走完一半时间后，他将以V2的速度前进，此时的运动图像应该与甲的平行，而此时的平行也决定着乙先到达目的地，从而反证出Vs

在物理的学习过程中，数学是一项工具，而这项工具的巧妙使用却是一门艺术，教师要用自己的智慧将数学与物理勾画出美丽的火花，这是人类智慧与学科魅力巧妙碰撞的胜利之花，美且永恒.