基于方波脉冲外场的超冷原子-分子绝热转化∗
秦燕 栗生长
(西安交通大学理学院,西安 710049)
基于受激拉曼绝热通道技术,研究了方波脉冲外场下的超冷原子-双原子分子转化.运用绝热保真度的方法,详细分析了该原子-分子转化系统相干布居俘获态的动力学演化过程.研究发现,相干布居俘获态的最终绝热保真度随脉冲激光强度的变化呈现出大幅度的周期振荡.这表明本文所设计的方波脉冲方案与高斯脉冲方案相比具有明显的优势,可以在较小的脉冲激光强度下达到较高的绝热保真度并实现较高效率的超冷原子-分子转化.
1 引 言
近年来,关于超冷原子-分子转化的研究已经成为物理学界,尤其是低温物理和原子分子物理等领域的热点课题之一.超冷分子因其具有极低的温度和丰富的内部能级而具有非常广泛的应用.超冷极性分子具有永久电偶极矩[1],可以产生可调控的各向异性长程偶极-偶极相互作用,再结合对分子自由度的精确操控,使其在量子计算[2]和量子模拟[3]等方面有重要用途.此外,超冷分子在超冷化学[4]、精密测量[5]、探测基本对称性[6]、量子信息处理[7,8]、分子退相干[9]和分子光学[10]等方面也有重要应用.
由于分子的自由度相对比较复杂,所以制备冷原子的技术无法简单有效地拓展到分子体系.为此,科学家们发展了许多制备超冷分子的实验方法.为了冷却与俘获分子,人们通常采用直接冷却和间接冷却两种方法来产生超冷分子.直接冷却分子的技术包括缓冲气体冷却[11]、斯塔克减速[12]、塞曼减速[13]、速度滤波[14]、协同冷却[15]和偏振梯度冷却[16]等.然而,这些直接冷却方法通常只能将温度降低到毫开尔文量级.间接冷却分子的技术主要通过Feshbach共振(Feshbach resonance,FR)[17,18]和光缔合(photoassociation,PA)[19,20]技术将超冷原子转化成超冷分子.但是,FR技术和PA技术通常都只能将超冷分子制备在不稳定的态上.
实际上,受激拉曼绝热通道(stimulated Raman adiabatic passage,STIRAP)技术[21−24]是一种更加有效的制备超冷分子的方法.该技术的成功依赖于相干布居俘获态(coherent population trapping state,CPT态)[25]的存在.在CPT态上,分布在激发态上的粒子数布居几乎为零,CPT态的绝热演化能有效地抑制激发态上粒子的自发辐射,从而达到从原子到稳定分子的高效转化.目前,已有科研工作者采用FR,PA和Ef i mov共振[26]辅助的STIRAP来获得多体聚合物分子[27].
文献[28]运用STIRAP技术研究了高斯脉冲外场下超冷原子-分子的高效率转化问题,该方案需要较高的脉冲激光强度,实现起来比较困难.为了解决这一问题,本文提出一种新的方案,即利用方波脉冲外场来研究原子-分子转化系统CPT态在STIRAP中的绝热演化过程,以达到用小的脉冲激光强度得到高的原子-分子转化效率的目的.
2 理论模型
本文考虑典型的Λ型三能级超冷原子-双原子分子转化系统,理论模型如图1(a)所示.初态为原子态,记为|1⟩,中间态为分子激发态,记为|2⟩,它们之间用一束抽运激光进行耦合,对应的拉比频率为,失谐为∆.目标态为分子基态,记作|3⟩,它和中间态|2⟩用一束斯托克斯激光进行耦合,对应的拉比频率为失谐为δ.这里假设拉比频率都是正实数.在双光子共振条件下,δ=0,本系统二次量子化的哈密顿量可以写成[29,30]:

其中~=h/(2π)为约化普朗克常数,H.c.表示厄米共轭,Ψ和分别对应态|i⟩(i=1,2,3)的湮灭和产生算符.在平均场近似下,可将湮灭算符和产生算符分别替换成相应的复数Ψi和,这样就可以得到描述系统动力学的平均场方程,即非线性薛定谔方程:

其中˙x表示x对时间t的一阶导数.文献[31,32]给出了超冷原子-分子转化系统本征值为零的CPT本征态为:


图1 (a)由两束激光耦合的三能级超冷原子-分子转化系统能级示意图;(b)激光场的拉比频率随时间的变化关系Fig.1. (a)Schematic diagram of the three-level ultracold atom-molecule conversion system coupled with two laser beams;(b)time dependence of the Rabi frequencies

本文引入两个绝热保真度对超冷原子-分子转化的效率进行描述:1)最终绝热保真度Ff,它是演化结束时绝热保真度的值,这个量越接近于1,表明转化效率就越高;2)最终最大绝热保真度,它是演化结束时保真度所能达到的最大值,表示最终能达到的最高转化效率.下面利用这两个量来详细研究超冷原子-分子转化系统CPT态的绝热演化过程.
3 结果与分析
3.1 绝热保真度随时间的演化
在本文讨论的超冷原子-分子转化方案中,两束脉冲激光场均采用如下的方波形式:
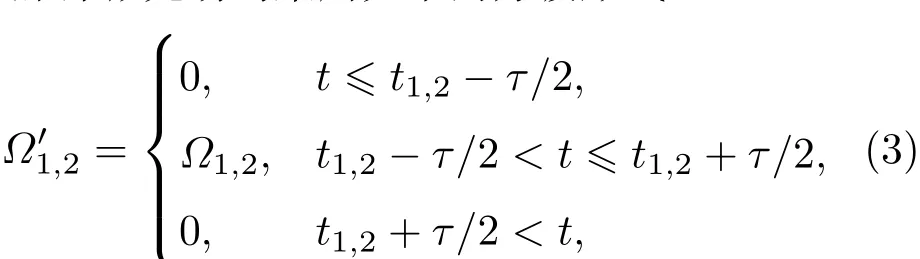
其中Ω1,2分别为斯托克斯激光和抽运激光的强度,t1,2对应脉冲的中心位置,τ为脉冲宽度,∆t=t2−t1描述两束脉冲激光输入的延迟时间,如图1(b)所示.
在本文的讨论中,只考虑∆=0的共振情形,取第一个脉冲的中心位置为t1=5同时固定两脉冲激光的宽度为τ=1.5,这样第二个脉冲的中心位置就可以通过t2=t1+∆t确定.|CPT⟩的表达式要求=0,因此,在数值求解非线性薛定谔方程(2)时,′在t 6 t1,2−τ/2和t1,2+τ/2 为了解CPT态在演化过程中的绝热保真度变化情况,先固定脉冲延迟时间∆t=0.5,然后改变脉冲激光强度并计算F(t),结果如图2(a)—(c)所示.可以看出,当两束脉冲激光强度相同时(图2(a)),脉冲激光强度越大,脉冲结束后的绝热保真度(即最终绝热保真度)越低.当两束脉冲激光强度不同时,第一束脉冲激光的强度越大(即Ω1/Ω2越大),脉冲结束后的绝热保真度越低(图2(b)),第二束脉冲激光的强度越大(即Ω2/Ω1越大),脉冲结束后的绝热保真度也越低(图2(c)).同样,也可以先固定脉冲激光的强度再改变两脉冲激光的延迟时间并计算F(t),结果如图2(d)—(f)所示.不难发现,当两脉冲强度相同时,延迟时间越长,最终绝热保真度越低(图2(d)).当第一束脉冲激光强度大于第二束脉冲激光强度(图2(e))或第一束脉冲激光强度小于第二束脉冲激光强度(图2(f))时,延迟时间越长,最终绝热保真度有可能越高也有可能越低.其实,图2(a)—(c)的相干性相同,但由于图2(a)和图2(c)绝热性好,所以最终绝热保真度高,而图2(b)绝热性差,所以最终绝热保真度低.图2(d)—(f)的相干性不同,由于图2(d)和图2(f)绝热性好,相干性的影响较小,所以最终绝热保真度高,但图2(f)绝热性差,所以最终绝热保真度低. 图2 绝热保真度F随时间t的变化关系 (b),(e)Ω2=10;(c),(f)Ω1=10Fig.2.Time evolution of the adiabatic f i delity F:(b),(e)Ω2=10;(c),(f)Ω1=10. 图2 还显示无论两束脉冲激光的强度如何,在两脉冲重叠的区域,绝热保真度均随时间做周期振荡.为描述绝热保真度在脉冲重叠区域的这种周期振荡特性,这里引入两个物理量:绝热保真度的振荡周期,记为TΩ和T(Ω1/Ω2)(或T(Ω2/Ω1)),分别描述脉冲强度相同和不同的情况;绝热保真度的振荡强度,描述振荡过程中绝热保真度能达到的最大值,记为FΩ 和F(Ω1/Ω2)(或F(Ω2/Ω1)). 计算结果如图3所示,可以看出,当两束脉冲激光的强度相同时,绝热保真度在脉冲重叠区域的振荡周期很短,这意味着F(t)做快速振荡,且振荡周期TΩ随脉冲强度Ω的增大而缓慢减小(图3(a)).值得注意的是此时振荡强度FΩ不随脉冲强度Ω发生任何改变,保持在0.746(如图3(b)所示).当两束脉冲激光的强度不同时, 振荡周期T(Ω1/Ω2)(或T(Ω2/Ω1))较长,说明F(t)做慢速振荡,且振荡周期随脉冲强度比值Ω1/Ω2(或Ω2/Ω1)的增大而快速减小(如图3(c)和图3(e)所示).不同的是在这种情况下,绝热保真度的振荡强度F(Ω1/Ω2)(或F(Ω2/Ω1)) 不再保持恒定,将随脉冲强度比值的增大而迅速增大(如图3(d)和图3(f)所示).当然,绝热保真度在这个过程中所能完成的振荡次数完全取决于两脉冲的重叠时间,脉冲延迟时间∆t越短,脉冲重叠时间就越长,相干性就越好,完成的振荡周期就越多. 图3 脉冲重叠区域绝热保真度的振荡周期和振荡强度随脉冲强度的变化Fig.3.Periods and intensities of the oscillations of F(t)in the pulse-overlap region vs.the intensities of the pulses. 图4 不同脉冲激光强度时原子基态和分子基态的布居几率随时间的变化 (d)—(f)Ω2=10;(g)—(i)Ω1=10Fig.4.Time evolution of the occupation probabilities of the atomic ground state and the molecular ground state for dif f erent intensities of the pulses:(d)–(f) Ω2=10;(g)–(i) Ω1=10. 上面讨论的绝热保真度描述系统演化过程中CPT态与真实态之间的距离,为展示绝热保真度和真实态演化的关系,下面给出系统随时间的真实演化图像.对方波脉冲激光作用下的超冷原子-分子转化系统,这里只关注演化中系统原子基态和分子基态的粒子布居情况,分别用ρa和ρm来表示,且ρa=|Ψ1|2,ρm=|Ψ3|2. 图4给出了系统在方波脉冲外场作用下从原子基态开始演化的情况,可以发现当脉冲延迟时间一定时,即∆t=0.5,系统的原子-分子转化过程和效率与脉冲激光的强度关系密切.总体看来,两束脉冲激光强度相同时(图4(a)—(c))和第二束脉冲激光强度较大时(图4(g)—(i))转化效率较高,而当第一束脉冲激光强度较大时转化效率不理想,甚至转化有可能被抑制(图4(f)).显然,图4中脉冲延迟时间相同,这意味着相干性相同,由于图4(a)—(c)和图4(g)—(i)的绝热性好,因此相干布居转移成功,最终分子基态粒子布居多.然而,图4(d)—(f)绝热性差,所以相干布居转移不好,最终分子基态粒子布居少.作为比较,也可以在脉冲激光强度一定的情况下讨论脉冲延迟时间对分子基态布居几率演化过程的影响,以及对最终原子-分子转化效率的影响,结果如图5所示.图5表明要成功实现相干布居转移,绝热性和相干性都要有保证,如图5(h),由于相干条件和绝热条件都满足,所以最终分子基态粒子布居占绝对优势. 图5 不同脉冲延迟时间时原子基态和分子基态的布居几率随时间的变化 (d)—(f)中Ω2=10;(g)—(i)中Ω1=10Fig.5.Time evolution of the occupation probabilities of the atomic ground state and the molecular ground state for dif f erent pulse-delay time: (d)–(f): Ω2=10;(g)–(i): Ω1=10. 通过前面的分析和讨论,已经明确了绝热保真度和原子-分子转化效率之间的关系.当脉冲激光结束后也就是系统演化结束时,若超冷原子几乎全部转化成超冷分子,转化效率高,对应的最终绝热保真度接近于1;若转化效率低,最终绝热保真度就小.接下来重点探讨脉冲延迟时间和脉冲激光强度对最终绝热保真度的影响,旨在找出使最终绝热保真度最大,即实现高效超冷原子-分子转化的脉冲激光参数. 首先讨论脉冲延迟时间对最终绝热保真度的影响.对不同的脉冲强度分别计算最终绝热保真度随脉冲延迟时间的变化,结果如图6所示.若两脉冲强度相同,最终绝热保真度将随脉冲延迟时间做周期振荡,且脉冲强度越大,振荡频率越高(见图6(a),(d)和(g)).若第一束脉冲激光的强度大于第二束脉冲激光的强度,最终绝热保真度也随脉冲延迟时间做周期振荡,只不过振荡先衰减后稳定,且第一束脉冲激光强度越大,振荡频率越高(见图6(b),(e)和(h)).若第二束脉冲激光的强度大于第一束脉冲激光的强度,最终绝热保真度也随脉冲延迟时间做周期振荡,但第二束脉冲激光强度的增加并不会导致最终绝热保真度的振荡频率明显变大(见图6(c),(f)和(i)).特别需要指出,对于Ω1≫ Ω2的情况(图6(h)),最终绝热保真度Ff随脉冲延迟时间∆t的振荡强度非常小,这意味着最终的原子-分子转化效率很低.其实,图6(a),(d),(g),(c),(f)和(i)绝热性都很好,随着脉冲延迟时间的增加相干性保持得很好,所以最终可以实现高效的原子-分子转化.图6(b),(e)和(h)绝热性差,随着脉冲延迟时间的增加相干性降低,所以振荡衰减且最终原子-分子转化效率低. 图6 最终绝热保真度Ff随脉冲延迟时间∆t的变化 (b),(e),(h)Ω2=10;(c),(f),(i)Ω1=10Fig.6.Final adiabatic f i delity Ffvs.the pulse-delay time∆t:(b),(e),(h)Ω2=10;(c),(f),(i)Ω1=10. 接着讨论脉冲激光强度的变化对最终绝热保真度的影响. 对不同的脉冲延迟时间,分别计算最终绝热保真度Ff随脉冲激光强度Ω,Ω1/Ω2(Ω2=10) 及 Ω2/Ω1(Ω1=10)的变化情况,计算结果如图7所示.若两脉冲强度相同,即Ω1=Ω2=Ω,对一定的脉冲延迟时间,最终绝热保真度随脉冲强度做周期振荡,且振荡周期随脉冲延迟时间的增加而增加,振荡的强度变化很小(见图7(a),(d),(g)).若第一束脉冲激光的强度大于第二束脉冲激光的强度,最终绝热保真度随脉冲强度的比值Ω1/Ω2做周期振荡,且振荡周期随脉冲延迟时间的增加而增加,但振荡的强度随Ω1的增加衰减很快(见图7(b),(e),(h)).若第二束脉冲激光的强度大于第一束脉冲激光的强度,最终绝热保真度随脉冲强度比值Ω2/Ω1的增加先变大后减小,周期振荡行为消失,变化规律较为复杂.当脉冲延迟时间∆t=0.5时(见图7(f)),最终绝热保真度随Ω2的增长很快、衰减很慢,但当脉冲延迟时间∆t=0.4(见图7(c))和1.1(见图7(i))时,最终绝热保真度随Ω2的增长和衰减都很快.值得注意的是,无论脉冲延迟时间长短,最终绝热保真度在随脉冲激光强度变化的过程中,它所能达到的最大值都相差不大,且比较接近1,这说明对固定的脉冲延迟时间,总能找到合适的脉冲激光强度参数从而实现高效的原子-分子转化.图7的结果充分展示了脉冲延迟时间对绝热性的影响,说明绝热性跟相干性密切相关,相互影响. 对于∆t=0.5且Ω2/Ω1>1的情况,本文的结果(见图7(f))与用高斯型脉冲外场得到的结果类似[28].可以认为Ff增大到一定程度后就会基本趋于稳定,稳定值在0.9到1.0之间,这说明随着Ω2的进一步增加,虽然系统的绝热性会下降,但STIRAP过程仍然可以实现高效的原子-分子转化.其物理原因在于原子-分子转化过程中,随着原子基态|1⟩布居几率的减少,它与分子激发态|2⟩之间的有效耦合强度Ω2|Ψ1|就会变弱,但通过增加抽运激光的拉比频率(即脉冲激光强度)Ω2可以及时地弥补有效耦合强度的减小,从而增强双光子过程,最终达到实现高效原子-分子转化的目的[28]. 图7 最终绝热保真度Ff随脉冲激光强度Ω,Ω1/Ω2和Ω2/Ω1的变化 (b),(e),(h)Ω2=10;(c),(f),(i)Ω1=10Fig.7.Final adiabatic f i delity Ffvs.the pulse-laser intensity Ω, Ω1/Ω2,and Ω2/Ω1:(b),(e),(h) Ω2=10;(c),(f),(i)Ω1=10. 从上面的讨论可以看出,当两脉冲激光强度相同时,最终绝热保真度Ff随Ω做周期振荡的行为很明显,只是振荡强度略有起伏(见图7(a),(d),(g)).为进一步分析这种情况,可以对不同脉冲延迟时间∆t下最终绝热保真度的振荡周期进行统计,结果如图8(a)所示.不难发现,最终绝热保真度Ff随脉冲强度Ω做周期振荡所对应的振荡周期T∆t随着脉冲延迟时间的增大而明显增大,当脉冲延迟时间较短时(如∆t<1.2),T∆t增长缓慢,当脉冲延迟时间较长时(如∆t>1.3),T∆t急剧增长.在周期振荡过程中,最终绝热保真度的最大值也就是最终最大绝热保真度max对脉冲延迟时间的依赖关系,如图8(b)所示.显然,最终最大绝热保真度对脉冲延迟时间的变化并不敏感,一直维持在0.95左右,说明原子-分子的转化效率在等脉冲强度的情况可以达到95%左右.当然,要实现这样的高效转化,所使用的两束脉冲激光的延迟时间和脉冲强度之间应该满足如图8(c)所示的关系.如果所采用的脉冲延迟时间较短(如∆t<1.2),需要的脉冲激光强度就很小(Ω<20),若采用的脉冲延迟时间较长(如∆t>1.4),需要的脉冲激光强度就要特别大(可能Ω >100). 图8 (a)最终绝热保真度随脉冲激光强度振荡的周期T∆t与脉冲延迟时间∆t的关系;(b)最终最大绝热保真度 ax与脉冲延迟时间∆t的关系;(c)最终最大绝热保真度所对应的脉冲强度Ω与脉冲延迟时间∆t的关系Fig.8.(a)Period of the oscillations of the fi nal adiabatic fi delity with the pulse-laser intensity,i.e.,T∆tvs the pulse-delay time∆t;(b) fi nal maximum adiabatic fi delity axvs.the pulse-delay time∆t;(c)the pulse intensityΩ (corresponding to the fi nal maximum adiabatic fi delity)vs.the pulse-delay time∆t. 对两脉冲强度不同的情况,同样可以计算并分析最终最大绝热保真度Ffmax随脉冲延迟时间的变化情况.考虑到Ω1/Ω2>0的情况对实现高效的原子-分子转化帮助不大,这里不再讨论.下面重点讨论Ω2>Ω1时最终最大绝热保真度对脉冲强度和延迟时间的依赖关系.如图9(a)所示,Ffmax先随Ω2/Ω1(Ω1=10)的增大而迅速增加,当增加到某一临界值后又随Ω2/Ω1的增大而缓慢减小,且在最后达到一稳定值.与最终最大绝热保真度相对应的脉冲延迟时间∆t和脉冲强度比值Ω2/Ω1之间满足的关系较为复杂,如图9(b)所示.∆t先随Ω2/Ω1的增大而急剧增大,在Ω2/Ω1≃2.09处∆t从0.404跳跃到1.125;之后在Ω2/Ω1达到30.33前,∆t一直缓慢增加,当Ω2/Ω1≃ 3 0.33时,∆t≃ 1 .149;当30.33< Ω2/Ω1<31.37时,∆t在I,II和III处的三个值之间跳跃;当 3 1.37< Ω2/Ω1<35时,∆t在I和III处的两个值之间跳跃,其中I,II,III处分别对应的∆t值约为0.548,1.149和1.183. 接下来对∆t这几次奇怪的跳跃行为进行解释,由图6(c),(f)和(i)知,最终绝热保真度Ff随脉冲延迟时间∆t做周期振荡,但每个周期振荡的强度略有差别,因此最终最大绝热保真度有可能出现在第一个振荡周期,也有可能出现在第二个振荡周期.对∆t发生在Ω2/Ω1≃ 2.09处的第一次跳跃恰好说明最终最大绝热保真度在Ω2/Ω1≃2.09前后分别出现在振荡的第一个周期和第二个周期(见图6(c)和图6(f)),跳跃前后的∆t的差别1.125−0.404=0.721可近似给出Ω2/Ω1≃2.09时最终绝热保真度的振荡周期.发生在Ω2/Ω1≃30.33处的第二次跳跃与第一次跳跃类似,只不过这时最终绝热保真度的最大值可能出现在第一个振荡周期的一处(∆t≃0.548)和第二个振荡周期的两处(∆t≃1.149和∆t≃1.183),具体可参考图6(i).发生在Ω2/Ω1≃31.37处的第三次跳跃与第一次跳跃完全类似,最终绝热保真度的最大值只可能出现在第一个振荡周期的一处(∆t≃0.548)和第二个振荡周期的一处(∆t≃1.183).可以看出,这些现象其实都是由于最终绝热保真度并不严格随脉冲延迟时间做周期振荡造成的. 图9 (a)最终最大绝热保真度 ax随Ω2/Ω1的变化;(b)最大最终绝热保真度所对应的∆t与Ω2/Ω1的关系 ( Ω1=10)Fig.9.(a)Final maximum adiabatic fi delity axvs.Ω2/Ω1;(b)∆t(corresponding to the fi nal maximum adiabatic fi delity)vs.Ω2/Ω1(Ω1=10). 综上,这里做两点讨论:1)作为拓展和补充,本文还探讨了激光脉冲宽度对超冷原子-分子转化效率的影响,如图10所示,最终绝热保真度随脉冲宽度做周期性振荡,这意味着可以用较小的脉冲宽度实现高效的原子-分子转化;2)为讨论连续光的可行性,本文以典型的正弦型激光为例进行计算,结果表明采用连续光在一定的条件下也可以实现原子-分子的高效转化. 图10 最终绝热保真度Ff随脉冲宽度τ的变化(Ω1=10)Fig.10.Final adiabatic f i delity Ffvs.the width of pulses τ(Ω1=10). 本文基于受激拉曼绝热通道技术详细研究了方波型脉冲激光外场作用下的超冷原子-分子转化情况,通过对最终绝热保真度和最终最大绝热保真度的计算分析得到了实现高效原子-分子转化时脉冲激光强度和脉冲延迟时间之间应该满足的条件以及最优的脉冲宽度.研究表明,本文提出的方案可以通过小的脉冲激光强度实现高效的超冷原子-分子转化,这与高斯型脉冲激光相比优势非常明显.这里给出两组数据对方波脉冲和高斯脉冲两种方案进行比较:对激光脉冲强度相同的情况,取t1=5,τ=1.5,系统演化时间为20,要使最终绝热保真度达到0.97,方波脉冲需要的激光强度为20.06,高斯脉冲需要的激光强度为327.04;要使最终绝热保真度达到0.95,方波脉冲需要的激光强度为14.54,高斯脉冲需要的激光强度为176.5.
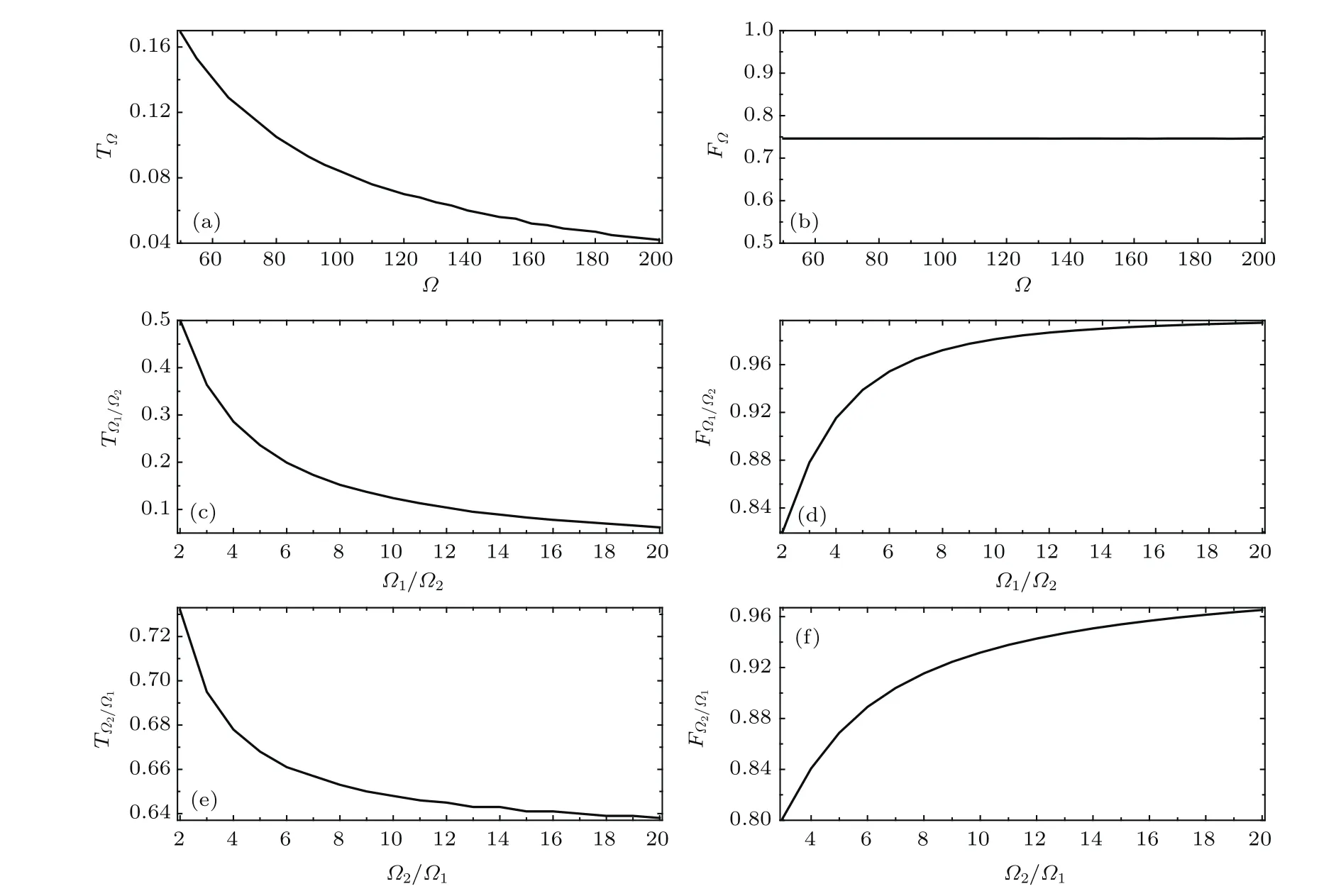


3.2 最终绝热保真度与脉冲延迟时间和脉冲强度的关系
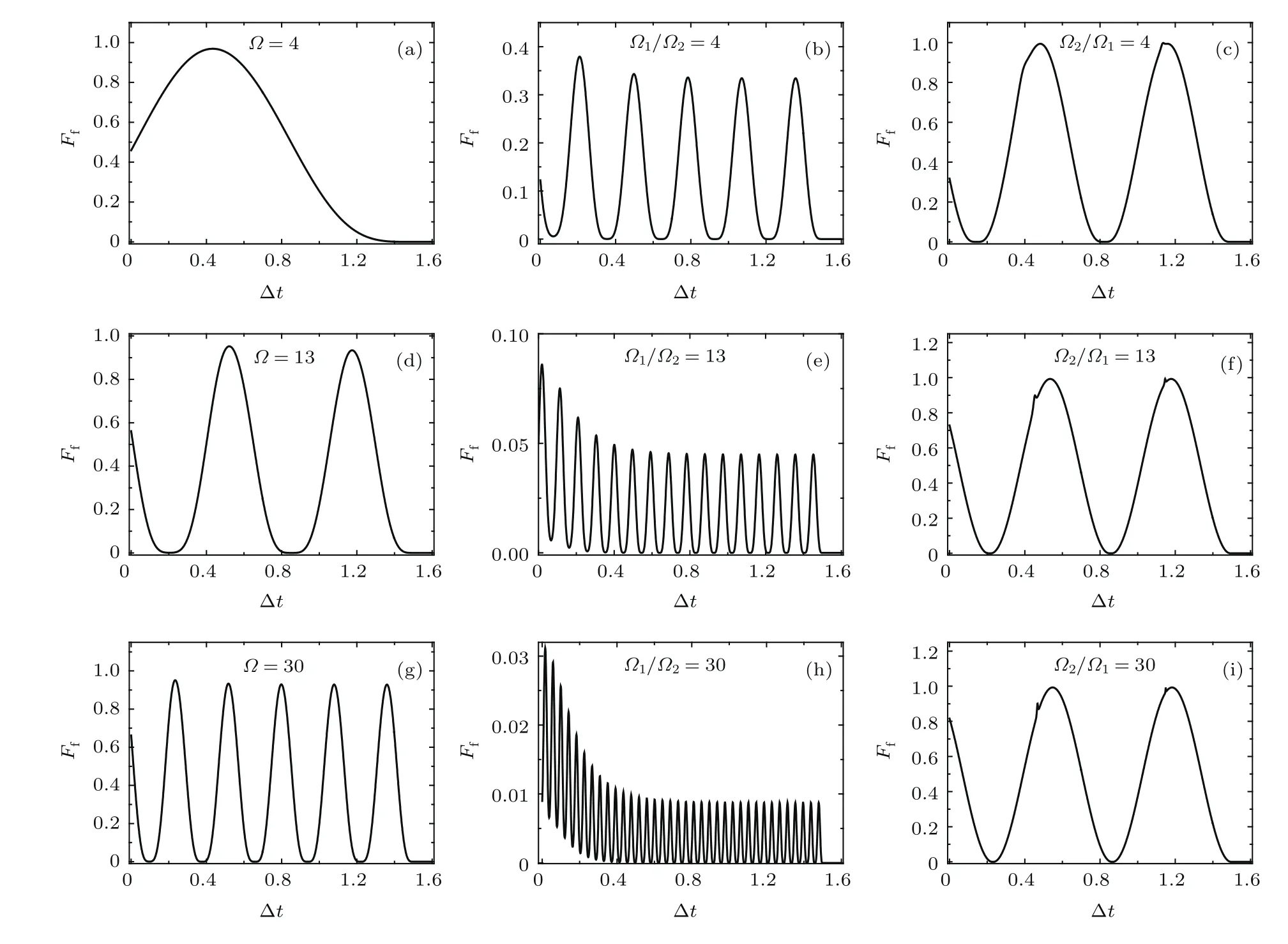

3.3 最终最大绝热保真度与脉冲延迟时间和脉冲强度的关系


4 讨论与总结


