一级磁结构相变材料Mn0.6Fe0.4NiSi0.5Ge0.5和Ni50Mn34Co2Sn14的磁热效应与磁场的线性相关性∗

张虎 邢成芬 龙克文 肖亚宁 陶坤 王利晨 龙毅

1)(北京科技大学材料科学与工程学院,北京 100083)

2)(佛山市程显科技有限公司,佛山 528513)

3)(佛山市川东磁电股份有限公司,佛山 528513)

4)(首都师范大学物理系,北京 100048)

磁熵变(∆SM)与磁场(µ0H)的相关性已在很多二级相变材料中被研究并报道,但一级相变材料的磁热效应与磁场相关性还少有报道.本文在具有一级磁结构相变的Mn0.6Fe0.4NiSi0.5Ge0.5材料中研究发现∆SM与µ0H存在线性相关性,并通过麦克斯韦关系式的数值分析详细讨论了这一线性相关性的来源.同时,进一步发现在低磁场时,∆SM近似正比于µ0H的平方.该线性相关性同样在一级磁结构相变Ni50Mn34Co2Sn14材料中得到了印证.但由于一级磁弹相变LaFe11.7Si1.3材料相变温度具有更强的磁场依赖性,不具有∆SM的线性相关性,因此,本研究表明,当磁结构相变材料的相变温度具有弱磁场依赖性时,∆SM与µ0H具有线性相关性.进而,在磁场未达到相变饱和磁场以下,利用∆SM与µ0H的线性相关性可以有效推测更高磁场下的∆SM.

1 引 言

与传统的气体压缩制冷技术相比,基于磁热效应(magnetocaloric ef f ect,MCE)的磁制冷技术具有环境友好和节能高效等优点,因此受到广泛的关注[1−4].磁热效应可以由等温磁熵变(∆SM)和绝热温变(∆Tad)两种参数来表征[5].通常,磁制冷材料可以分为一级磁相变材料和二级磁相变材料[6].许多一级磁相变材料表现出大的磁热效应[7−11],但其磁热效应的工作温区往往很窄,且常伴有大的磁滞和热滞,这会大幅降低材料的制冷效率[12,13].相反,二级磁相变材料虽然磁热效应相对低,但其工作温区大且没有磁滞和热滞,使其在宽温区内具有大的磁制冷能力[14,15].因此,两种磁相变材料各有优缺点,近年来都被进行了广泛的研究[1,16].

无论从基础研究还是实际应用的角度,磁热效应与磁场的相关性都具有非常重要的意义,因为它不仅能够指导我们更好地理解和优化磁热效应,还能够帮助我们估测更高磁场下的磁热效应[6,17].利用平均场模型,Oesterreicher和Parker[18]推导出二级磁相变材料居里温度TC附近∆SM与磁场的相关性可以表达为|∆|∝ Hn,其中n=2/3.但后来发现,一些二级磁相变材料中n值明显偏离了2/3[19−21].Franco等[19,22]进一步证明二级磁相变材料中n=1+(1/δ)[1− (1/β)],其中δ和β是临界指数.并且,他们提出了一个唯象的“通用曲线”,可以用来有效地预测磁热效应和判断相变性质[15,23].但另一方面,由于一级磁相变的复杂性和多样性,针对一级磁相变材料磁热效应和磁场的相关性研究还相对较少[17,24].

MM′X(M,M′为过渡族元素,X为主族元素)合金是一种新型磁制冷材料,因发生顺磁Ni2In型六角相到铁磁TiNiSi型正交相的一级磁结构相变,表现出大磁热效应,故受到越来越多的关注.近期,研究发现MM′X合金存在∆SM和磁场µ0H的线性相关性[25,26],然而这一线性相关性的内在原因尚不清楚.本工作以具有一级磁结构相变的MM′X合金为基础,详细研究了一级磁结构相变材料的∆SM和µ0H的相关性,分析了产生线性相关性的内在机制,并对比了该线性相关性对其他一级磁结构/磁弹相变材料的适用性.

2 实 验

将纯度大于99.9 wt.%的组成元素按Mn0.6Fe0.4NiSi0.5Ge0.5,Ni50Mn34Co2Sn14,LaFe11.7Si1.3的化学成分进行配比,在氩气保护气氛下进行电弧熔炼.将熔炼好的铸锭密封在充有高纯氩气的石英管中进行退火处理,其中Mn0.6Fe0.4NiSi0.5Ge0.5铸锭在1123 K退火5 d并炉冷至室温,Ni50Mn34Co2Sn14在1173 K退火4 d并冰水淬火,LaFe11.7Si1.3在1373 K退火40 d并冰水淬火.室温X射线衍射(X-ray dif f raction,XRD)实验确认,除LaFe11.7Si1.3存在少量α-Fe第二相外(约4.4 wt.%),所有样品均形成了单相.采用MPMS SQUID VSM磁性测量设备对材料的热磁曲线和等温磁化曲线进行了测试,为了避免出现“伪巨磁熵变∆SM”[27,28],M-µ0H测量采用loop模式,即每条M-µ0H曲线测试前,先将样品加热至完全顺磁态,然后降温至目标测试温度[29,30].此外,M-µ0H曲线还进行了退磁校正,即Hint=Hext−NdM.

3 结果与讨论

图1(a)所示为Mn0.6Fe0.4NiSi0.5Ge0.5在不同磁场变化下的等温磁熵变−∆SM随温度变化的关系.由图1(a)可以看出,Mn0.6Fe0.4NiSi0.5Ge0.5表现出巨磁热效应,5 T磁场下在315 K的最大磁熵变−∆SM为38.0 J/(kg·K).这一巨磁热效应归因于从顺磁Ni2In型六角相到铁磁TiNiSi型正交相的一级磁结构相变[25].为进一步研究−∆SM的磁场相关性,图1(b)绘出了−∆SM峰值与磁场µ0H的依赖关系.可以看出当µ0H>1 T时,−∆SM与磁场存在线性依赖关系:

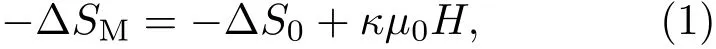
其中−∆S0为零磁场时的截距,κ是描述−∆SM对磁场依赖性的斜率.线性拟合的校正R方因子为0.99834,表明∆SM-µ0H曲线具有很好的线性依赖关系.但同时发现,在低场下出现了一定的偏差(图1(b)插图).下面将通过数值分析详细讨论高场下的线性相关性和低场下偏差出现的原因.

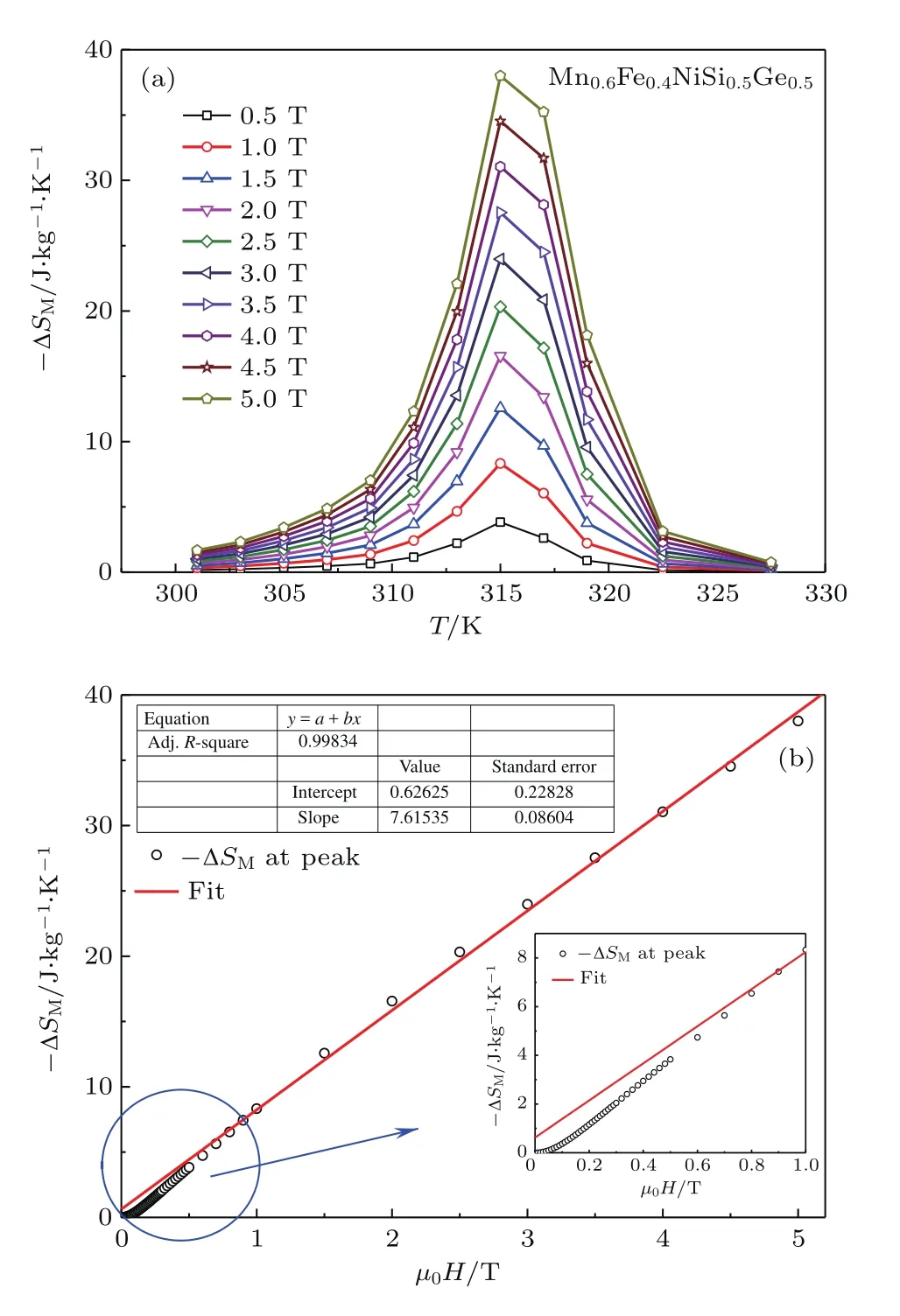
图1 (a)不同磁场变化下Mn0.6Fe0.4NiSi0.5Ge0.5的等温磁熵变−∆SM随温度的变化关系;(b)−∆SM峰值与磁场µ0H的依赖关系及线性拟合,插图为低场部分的线性拟合偏差Fig.1.(a)Temperature dependence of−∆SMfor Mn0.6 Fe0.4NiSi0.5Ge0.5compound under dif f erent magnetic f i eld changes;(b)−∆SMvalue at peak as a function ofµ0H,and the f i tting line to −∆SM-∆µ0H curve(the inset shows the−∆SM-∆µ0H curve and the f i tting line at low f i elds).

图2(a)所示为Mn0.6Fe0.4NiSi0.5Ge0.5的等温磁化曲线.在居里温度TC=312 K附近,磁化曲线在低场时随磁场迅速增加并趋于饱和,然后当µ0H>1 T时出现大的上升,表明发生了磁场诱导的从顺磁Ni2In型六角相到铁磁TiNiSi型正交相的变磁转变.同时,大的磁滞说明该相变性质为一级相变.根据等温磁化曲线,可以利用麦克斯韦关系式计算等温磁熵变∆6

,31]:

近些年,由于采用麦克斯韦关系式计算一级磁相变材料的磁熵变常常出现“伪巨磁熵变∆SM”,因此,其是否适用于一级相变磁熵变的计算存在很多争论[28,32−34].近期,Amaral等[35,36]发现麦克斯韦关系式产生“伪巨磁熵变∆SM”不是一级磁相变性质造成的,而是由于没有考虑两相共存的非平衡态以及测试过程对不同磁性的影响.进而,Caron等[1,29]指出,通过采用loop模式测试等温磁化曲线能够避免“伪巨磁熵变∆SM”的出现,因此,麦克斯韦关系式仍适用于一级磁相变.因为等温磁化曲线是在不连续的温度点下测得,所以麦克斯韦关系式可以近似为[12,31]

其中∆M为磁场Hi下降场磁化曲线M316K和M314K之间的差值.图2(b)所示为∆M/2与磁场的变化关系.根据(3)式,315 K时的磁熵变∆SM应为∆M/2-µ0H曲线的面积积分.由图2(b)可知,低场时由于铁磁相的磁化强度迅速增大导致∆M/2快速上升,随后在到达一个峰值后∆M/2开始缓慢下降.以该峰值∆Mmax/2为界可将∆SM分为两部分,第一部分∆SM1可以近似看为三角形,特别是在0.2 T以下斜率接近为常数.因此,∆SM1可以近似用如下表达式计算:

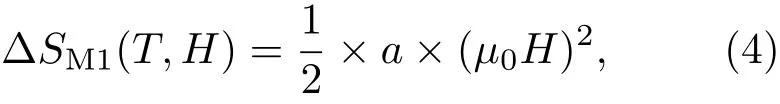
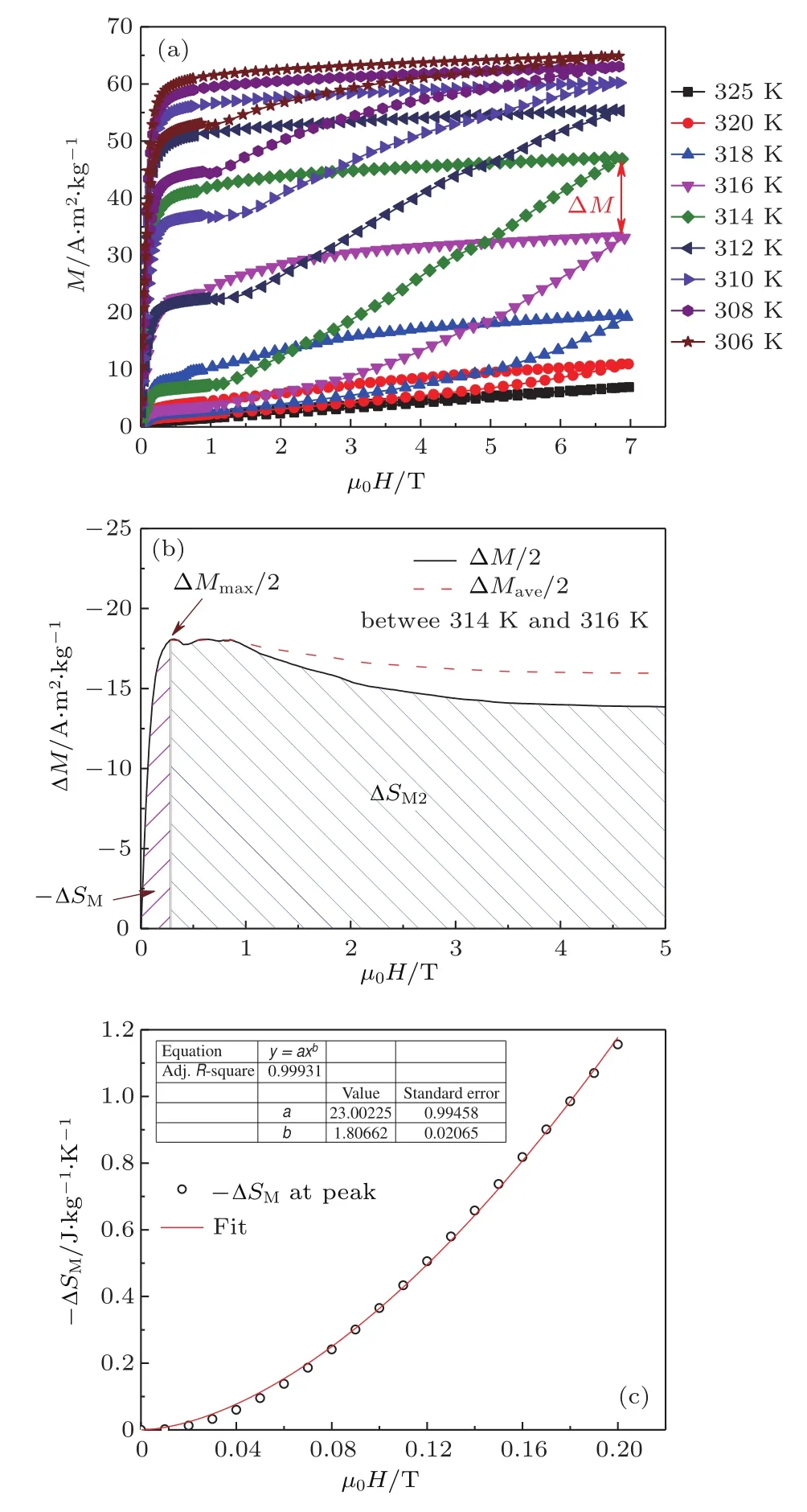
图2 (a)不同温度下Mn0.6Fe0.4NiSi0.5Ge0.5的等温磁化曲线;(b)314 K和316 K之间∆M/2与磁场µ0H的变化关系;(c)0.2 T磁场以下磁熵变−∆SM峰值与磁场的依赖关系及指数拟合Fig.2.(a)Magnetization isotherms of Mn0.6Fe0.4NiSi0.5 Ge0.5compound in loop process;(b)∆M/2 between 314 K and 316 K as a function of magnetic fi eldµ0H;(c)magnetic if eld dependence of−∆SMvalue at peak and the fi tting line at fi elds below 0.2 T.

其中a是该三角形的斜率.由(4)式可以看出,当a是常数时,|∆SM1|∝ H2.图2(c)为0.2 T磁场以下磁熵变−∆SM峰值与磁场的依赖关系及指数拟合.该曲线符合非线性指数拟合条件,磁场µ0H的指数拟合为1.81,接近2,证明了以上数值分析的合理性.

当磁场大于峰值∆Mmax/2的临界场µ0H∆Mmax/2时,∆SM= ∆SM1max+∆SM2,其中∆SM1max是∆Mmax/2以下的面积,为一个定值;而∆SM2是µ0H∆Mmax/2和最终磁场µ0H之间的积分面积.由图2(b)可见,∆SM2可近似看为梯形,因此,可用如下表达式计算:

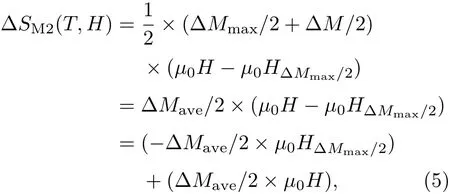
其中∆Mave/2是(∆Mmax/2+∆M/2)的平均值.根据(5)式,当磁场大于µ0H∆Mmax/2时,总的磁熵变∆SM为

从图2(b)可以看出,当µ0H>1 T时∆Mave/2近似为恒定值.通过对比(1)式和(6)式,(6)式中的第一个括号可看成(1)式中的−∆S0,(6)式中的第二个括号相当于(1)式中的κµ0H.因此,当µ0H>1 T时,−∆SM与磁场存在线性相关性.

通过以上数值分析和讨论,阐明了具有一级磁结构相变的Mn0.6Fe0.4NiSi0.5Ge0.5的∆SM-µ0H曲线在高场下的线性相关性和低场下偏差出现的原因.进一步,利用类似的数值分析,我们发现除了∆SM峰值外,其他温度的∆SM值与磁场也存在线性相关性,如图3所示.

因此,可以通过线性拟合的方式推测高场下的∆SM值.例如,通过插图中的线性拟合可以获得7 T磁场下不同温度的∆SM值.图3所示为7 T磁场变化下Mn0.6Fe0.4NiSi0.5Ge0.5的实验∆SM及拟合∆SM曲线.由图3可见,拟合∆SM曲线与实验曲线完全重叠,这一结果证实,可以利用∆SM值与磁场的线性相关性来预测更高磁场下的磁熵变值.需要指出的是,磁熵变来自于磁场诱导的相变,当磁场达到一定值后,相变完全,则磁熵变达到饱和,不再随磁场增加,线性相关性将不再存在.因此,该∆SM值与磁场的线性相关性只在磁场未达到相变饱和磁场以下成立.

∆SM与磁场µ0H的线性相关性在其他具有一级磁结构相变的MM′X合金中也被发现报道[25],本文工作进一步验证了该线性相关性在一级磁结构相变的MM′X合金中具有普适性.为了进一步验证∆SM值与磁场的线性相关性是否也适用于其他一级磁相变体系,我们进一步研究了Ni50Mn34Co2Sn14和LaFe11.7Si1.3的∆SM值与磁场µ0H的依赖关系(图4).需要指出的是,Ni50Mn34Co2Sn14经历的是一级马氏体磁结构相变,而LaFe11.7Si1.3则为一级磁弹相变.由图4可知,Ni50Mn34Co2Sn14的∆SM值与磁场µ0H具有很好的线性相关性,但LaFe11.7Si1.3的∆SM-µ0H曲线不符合线性相关性,这表明∆SM值与磁场µ0H的线性相关性不适用于非磁结构相变体系.

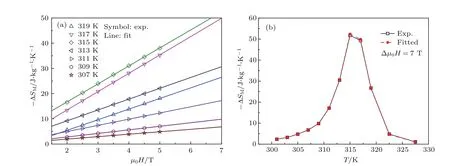
图3 (a)Mn0.6Fe0.4NiSi0.5Ge0.5在不同温度下−∆SM与磁场µ0H的依赖关系及线性拟合;(b)7 T磁场变化下Mn0.6Fe0.4NiSi0.5Ge0.5的实验∆SM及拟合∆SM曲线Fig.3.(a)−∆SMvalues at dif f erent temperatures around TCas a function ofµ0H and the f i tting lines to−∆SM-∆µ0H curves for Mn0.6Fe0.4NiSi0.5Ge0.5compound;(b)temperature dependences of experimental and f i tted∆SM for under magnetic f i eld change of 7 T for Mn0.6Fe0.4NiSi0.5Ge0.5compound.

由(6)式可知,只有当∆M随磁场变化近似为恒定值时才会出现∆SM值与磁场µ0H的线性相关性.图5(a)和图5(b)对比给出了LaFe11.7Si1.3和Mn0.6Fe0.4NiSi0.5Ge0.5在不同磁场下的热磁曲线.可以看出,两个样品都在居里温度TC附近发生了铁磁-顺磁相变.

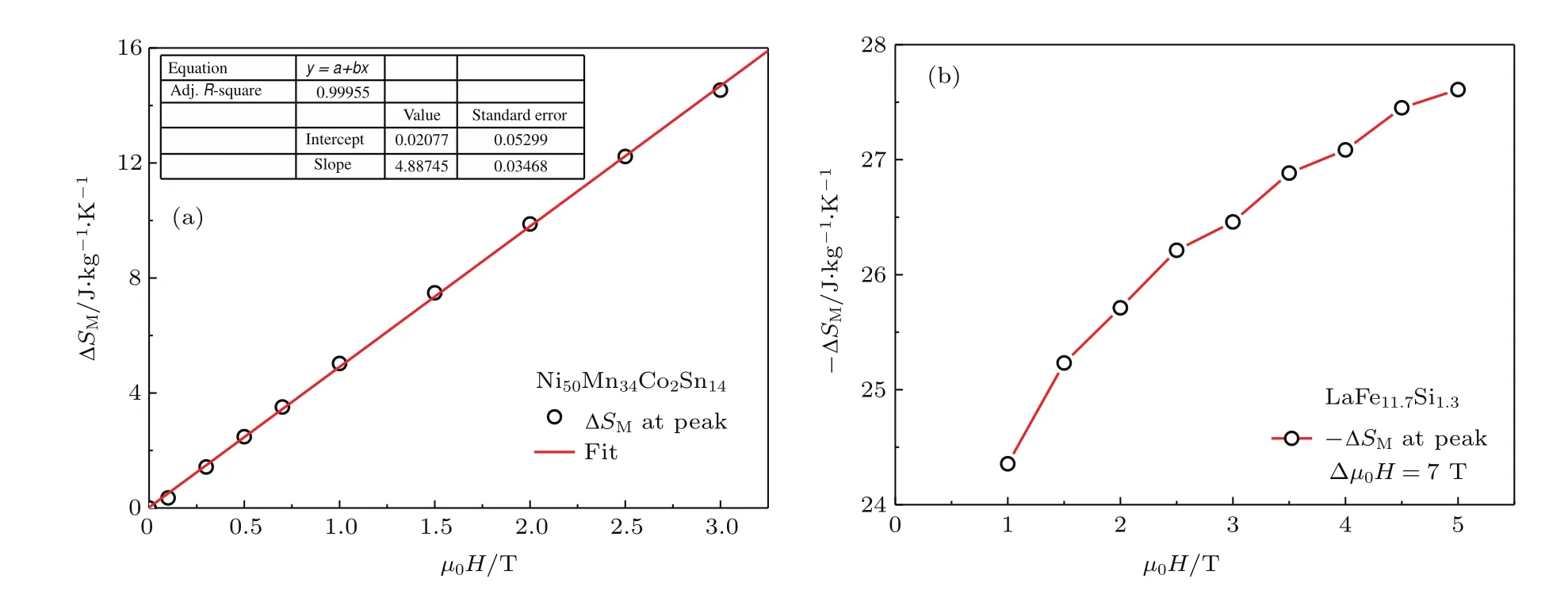
图4 (a)Ni50Mn34Co2Sn14和(b)LaFe11.7Si1.3的∆SM值与磁场µ0H的依赖关系Fig.4.The magnetic f i eld dependences of∆SMat peak for(a)Ni50Mn34Co2Sn14and(b)LaFe11.7Si1.3compounds,respectively.

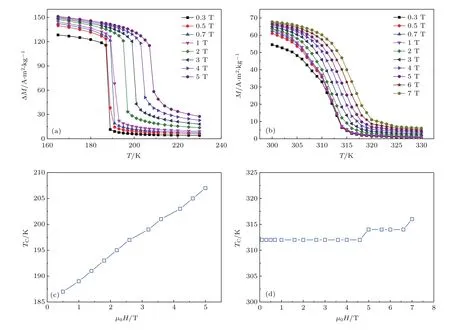
图5 (a)LaFe11.7Si1.3和(b)Mn0.6Fe0.4NiSi0.5Ge0.5在不同磁场下的热磁曲线;(c)LaFe11.7Si1.3和(d)Mn0.6Fe0.4 NiSi0.5Ge0.5的TC随磁场的变化关系Fig.5. Temperature dependences of magnetization in various magnetic f i elds for(a)LaFe11.7Si1.3and(b)Mn0.6Fe0.4NiSi0.5Ge0.5;magnetic f i eld dependence of TCfor(c)LaFe11.7Si1.3and(d)Mn0.6Fe0.4NiSi0.5Ge0.5,respectively.

居里温度TC是由dM/dT-T曲线的极小值所确定.图5(c)和图5(d)对比给出了LaFe11.7Si1.3和Mn0.6Fe0.4NiSi0.5Ge0.5的TC随磁场的变化关系.可以看出二者的区别在于,LaFe11.7Si1.3的TC随磁场增加显著向高温移动,导致T1和T2间的∆M随磁场变化而大幅变化,从而不具备线性相关性.相反,Mn0.6Fe0.4NiSi0.5Ge0.5的TC很难被磁场驱动,从而∆M不随磁场明显变化,因此满足(6)式的条件,出现∆SM值与磁场µ0H的线性相关性.类似地,Ni50Mn34Co2Sn14也同样具有TC难以被磁场驱动的情况.基于以上分析,表明当磁结构相变的转变温度具有弱磁场依赖性时,∆SM值与磁场µ0H表现出线性相关性.

4 结 论

我们发现一级磁结构相变Mn0.6Fe0.4NiSi0.5Ge0.5材料的∆SM值与磁场µ0H在高磁场时具有线性相关性,而在低场下出现偏差.通过麦克斯韦关系式的数值分析详细讨论了这一线性相关性以及低场偏差的来源,并发现低磁场时,∆SM近似正比于µ0H的平方.进一步在一级磁结构相变Ni50Mn34Co2Sn14材料中也印证了∆SM与µ0H的线性相关性,但一级磁弹相变LaFe11.7Si1.3材料不具有该线性相关性.深入分析发现,当磁结构相变的转变温度具有弱磁场依赖性时,∆SM值与磁场µ0H表现出线性相关性.在磁场未达到相变饱和磁场以下时,利用∆SM与µ0H的线性相关性能够帮助我们有效地预测高磁场下的∆SM值,可以作为很好的实验预测手段.

感谢西班牙塞利维亚大学物理系的Victorino Franco教授的讨论.