等离子环境中带电体能量的Collin变分
谭康伯 路宏敏 苏涛
(西安电子科技大学,天线与微波国家重点实验室,西安 710071)
基于系统性电磁兼容的考虑,对等离子环境中在轨航天器导体充放电现象中的能量特征进行了变分研究.通过电磁Collin原理,对等离子环境中导体系统几何尺度与所带电能的变分联系进行了理论分析.在此基础上,推广了更具一般性的数值估值分析方法,并对复杂导体系统电磁参数、等离子环境特征与系统能量间的关系进行了实例分析.研究结果对于等离子环境中复杂带电体的能量控制及相关的电磁环境效应与防护等研究具有积极意义.
1 引 言
等离子是物质存在的一种特殊形态[1−7],对处于其中的导体系统形成影响.在等离子环境工程中,导体充放电现象将导致在轨故障,对在轨航天器的有效运行以及功能发挥构成严重威胁[8−16].等离子环境中航天器的带电分析是系统性电磁兼容领域中需要持续研究的重点问题.
近年来,针对空间系统的静电防护,电磁结合统计的等离子环境的物理模拟为相关研究的不断深入提供了重要的基础支撑.从动力学角度来看,等离子环境中的导体系统会受到来自周围大量粒子的轰击,进而在系统表面形成电荷积累[10−15].这就构成了由导体与其周围等离子环境相关联的特殊动力学共同体,并呈现特定的能量规律.
对于动力学系统能量特征的探讨,变分方法原理简洁[17−21],在分析力学中有着重要的物理意义,可以深入刻画相关动力学的本质规律.在电磁研究中,变分方法对于系统特征的评估具有应用价值.因此,等离子环境中带电体能量的变分研究成为相关系统性电磁兼容理论研究中必须进一步深入探讨的问题.
本文基于变分原理,通过电磁Collin分析对等离子环境中与导体目标相关的能量估计问题进行讨论.
2 等离子中导体系统的Collin变分原理
在轨航天器与其周围等离子环境构成了特殊的动力学系统,其导体系统能量受两方面共同影响.一方面,由于等离子环境中具有一定能量的电子与离子随机运动[8−15],在导体表面上将产生带电粒子的聚集作用.在高温环境中,电子和离子有近似相同的热力学温度,即Te≈Ti.电子质量me远小于离子质量mi,处于平衡态时电子速度远大于离子速度,即ve≫vi.由统计理论可知,到达导体目标表面的电子数目将大于离子数目.于是,导体表面形成大量负电荷聚集,构成负电能积累.另一方面,由电磁理论可知[22,23],导体的静电能量为Ee=Q2/(2C),其中C是导体结构的电容,为导体系统自身属性,导体电位U及电量Q的变化受其约束.当导体处于电位稳定状态后,其静电特征满足关系:Q=CU.将该关系与导体系统能量关系共同考虑,可以得到

从(1)式可以看出,当导体电位确定时,孤立导体电容的变化与系统静电能量的变化间形成约束联系.
为了确定导体电位,需要借助于对电子和离子的聚集作用的分析.当导体系统处于等离子环境中时,由于导体表面负场阻碍作用的影响,电子只有沿表面法向具有大到足够克服相应负势能的能量时,才能到达导体表面.于是有能量关系:−eU=me⊥min/2,其中e为电子电量,ve⊥min为电子到达导体所具有的最小速率.在此基础上,依据等离子体中粒子的运动特性,从统计分析及麦克斯韦分布出发,可得电子流密度Γe为

其中k为玻尔兹曼常数,ne和ni为电子和离子密度.在粒子流作用下,等离子环境中孤立导体的电位平衡特征可由理论确定[13−15].负场的增强对电子向导体表面聚集形成阻碍作用,进而使流向导体表面的电子流密度逐渐减少,其中二次电子效应对表面电子数目也将产生影响.当到达孤立导体表面的电子流、离子流以及二次电子流作用平衡时,表面电位将达到稳定状态.此时有流平衡关系:Γe= Γi+Γse,其中,Γse为二次电子流密度.Γse= δeΓe+ δiΓi,其中δe为目标表面材料由电子引起的二次电子系数,δi则为由离子引起的二次电子系数.结合(2)式、(3)式,将其代入流平衡关系,可得(1)式中所需的平衡电位U.
由上面分析可知,在等离子环境中的带电导体系统呈现一定的能量特征,对其进行研究需要考虑电容的实际情况.Collin原理是变分在电磁研究中的重要延拓,可以对导体系统电容进行实用分析[24,25].为了探讨问题的内在联系,本文引入变分方法进行研究.由该原理可知,较大的孤立导体有着较大的电容.
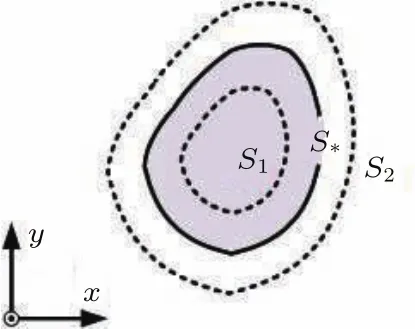
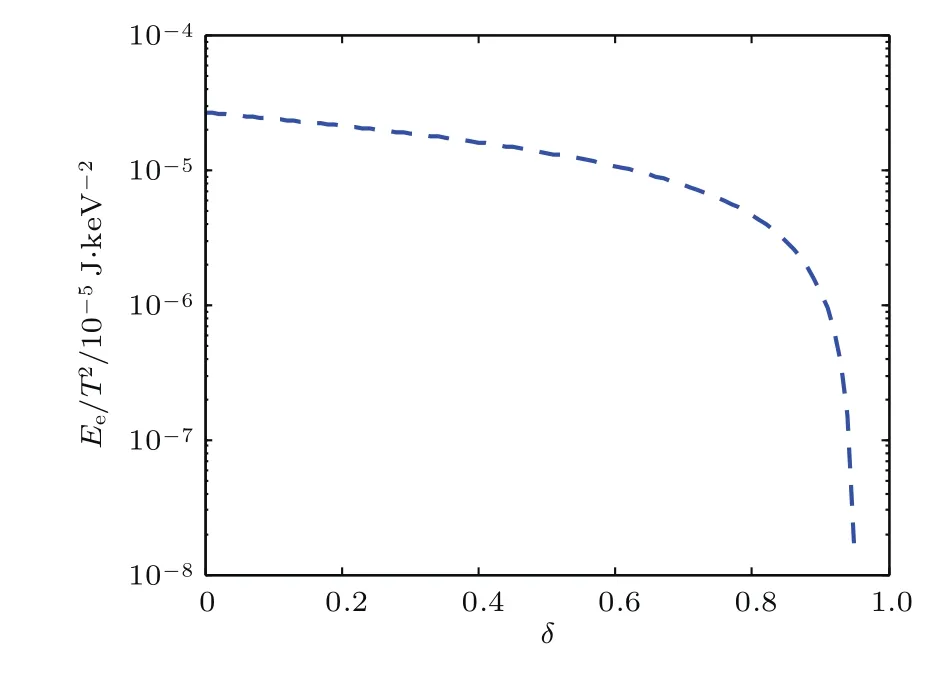
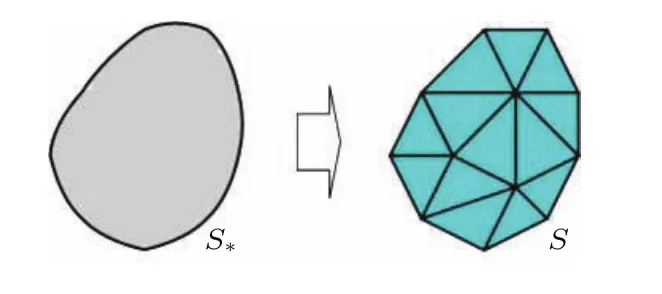
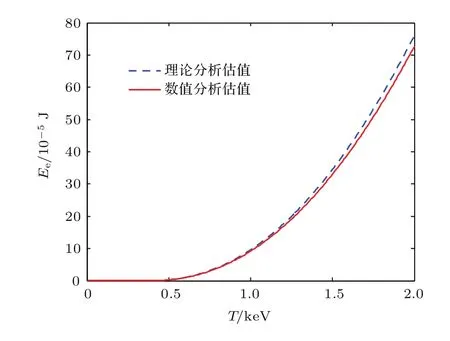
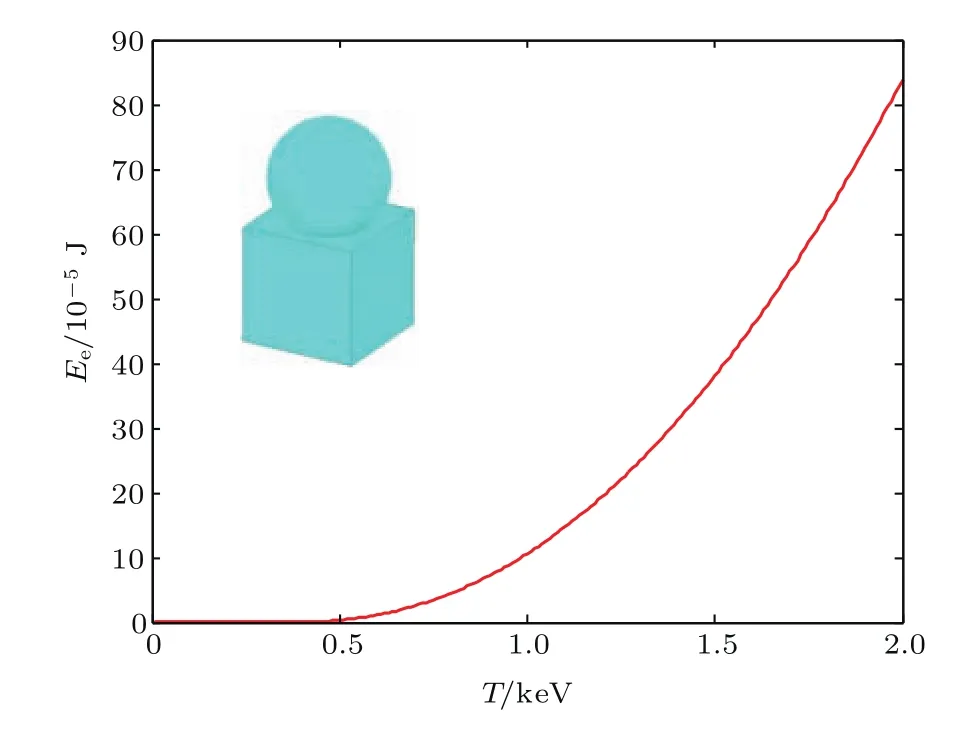
图1中所示的导体结构S1⊂S∗⊂S2,C1 在相同电位和相同平均电荷密度条件下,该形式表明相同的表面积有相同的总电荷,于是对应相同的电容.在此理论原理基础上,当电位得到一致性的确定后,由几何尺度所确定的电容将形成对于平衡态等离子系统中静电能的直接变分估计: 图1 Collin原理图Fig.1.Collin’s principle. 首先通过简单实例,对Collin变分分析的应用进行探讨.考虑空间尺度为a×a×a的方形导体目标.根据上一节中的变分条件,对该目标做相同表面积估值,所对应的等效半径为则可得到其相应的电容估值为 将(6)式代入(1)式,并结合所得平衡电位,可得平衡态下孤立方形导体电能的理论估值√为 从上面的结果可以看到,对于方形目标,电能与几何尺度在变分条件下成线性比例关系.该结果和文献[15]所得的电能与面积关系在物理上保持一致.对于电子所引起的二次效应,类似于[14,15,26,27],取δ= δi≈ δe且ni≈ ne,可得到二次电子效应对于带电体能量的影响,其结果如图2所示.显然,上面方法在对一些相对简单结构的电能特征的分析应用方面具有理论优势. 作为一种较好的实用分析方法,Collin变分原理为处理等离子环境中更复杂的导体系统提供了理论工具.为了有利于更普遍的应用,以面对复杂结构所提出的一般性分析要求,下面将基于变分原理(5)式,同时考虑等离子平衡态分析理论中的统计平均性,引入数值离散技术,对分析理论方法做进一步的推广. 图2 二次电子效应对等离子环境中带电立方体的影响Fig.2.Ef f ect of secondary electron emission on cube in plasma environment. 在等离子环境中,电子和离子流作用于导体系统表面的法向方向,形成电荷及能量积累.考虑到叠加特性,可将目标表面的待求区域进行N次离散剖分,以离散面片近似积分微元.通过离散,使得原有导体目标的几何构型S∗近似为离散剖分几何构型S,其过程如图3所示.平衡态时,设ρ表示目标上的电荷密度函数,则由空间电位关系可得如下积分算子方程: 其中L表示静场积分算子,R=|r−r′|,待求的未知函数是产生目标电位的电荷密度ρ. 图3 导体构型的空间离散Fig.3.Spatial discreteness of conductor con fi guration. 电子和离子流作用于各导体面片法向.根据几何构型进行离散,采用基函数fn将待求电荷密度函数展开,有从该式可以看出,只要求得系数an,就可进一步得到电荷密∫ 度 的分布情况.定义该问题的内积为将前面电荷密度的展开式代入内积表达式中,并且依据典型的矩阵向量形式[28],取检验采样函数为wm(r−rm),其中rm为每个离散面片的中点,以此标定法向流作用的空间特征.至此,(8)式转化为相应的矩阵代数方程: 其中lm,n= ⟨wm,Lfn⟩,bm⟨wm,U⟩. 通过求解上面矩阵代数方程,得到平衡态电荷密度分布函数的系数[an]=[lm,n]−1[bm],进而得到电荷密度函数.于是,在前面数值离散分析的基础上,即可得到等离子环境中相应导体目标的平衡态系统的能量估值: 通过理论分析可以看到,(10)式是(1)式在Collin原理下的离散近似,其结果与实际目标的离散度相关. 下面将基于Collin变分的离散方法应用于具体的等离子环境中导体目标的静电能量分析中,并进行讨论.分析中计及电子所引起的二次效应,并取T=Te≈Ti.首先,考虑处于等离子环境中a=0.5 m的立方导体,通过(7)式和(10)式,可以分别得到其静电能量理论分析和数值分析估值(图4). 图4 等离子环境中方形导体能量特征的估值对比Fig.4.Comparison for estimated energy of cube in plasma environment. 由上面结果可以看到,对于该方形导体目标,理论与数值分析具有一定的符合度.在等离子环境中,较高的等离子体温度对应于更为激烈的粒子运动,于是在粒子流作用下,导体结构上积累了更多能量.其次,考虑到数值途径为研究更复杂的导体系统提供了便利,下面给出具体实例分析.考虑半径为0.25 m球体子部分和边长为0.5 m立方体子部分的组合结构,其中两个子部分的体心间距为0.43 m,通过分析可以得到该带电系统在等离子环境中的能量特性(图5).由结果可知,在相同的等离子温度时,该组合系统较之单一立方体的几何形体更大,自身的能量更高.由于该组合结构较之方形于几何构型上的变化,在等离子温度为2 keV时,系统所带能量提升了约15.3%.通过分析可以看到,数值估值能够较为普遍地处理等离子环境中的复杂导体系统,在应用方面具有一定的一般性.值得注意的是,对于复杂系统,在研究其能量特性时,需具体考虑其整体几何构型特征. 图5 等离子环境中复杂系统的数值估值Fig.5.Numerical estimation of the composited system in plasma environment. 本文基于变分原理,探讨了导体目标几何构型与电能间的电磁Collin联系,对等离子环境中导体的电能进行了较为简洁的变分估值分析.出于Collin原理在处理复杂导体系统时实用性的考虑,在理论研究的基础上,本文结合数值分析技术,为等离子环境中导体系统电能的估值提供了更具实用价值的一般性分析方法.本文研究有利于等离子环境中复杂带电体的能量控制及相关的电磁环境效应与防护技术的深入.

3 实例分析和一般性数值推广
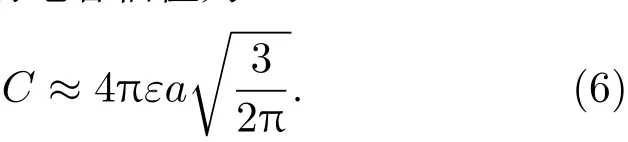
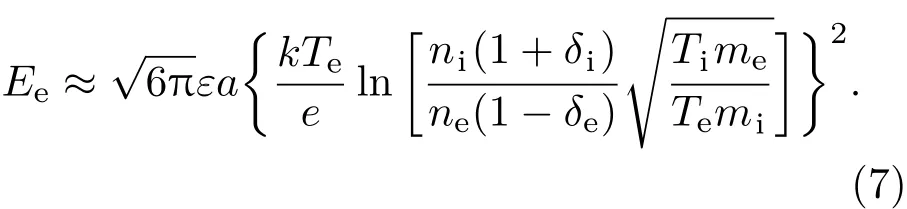
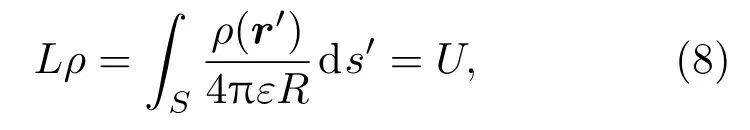
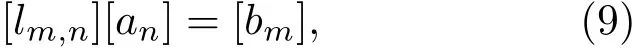
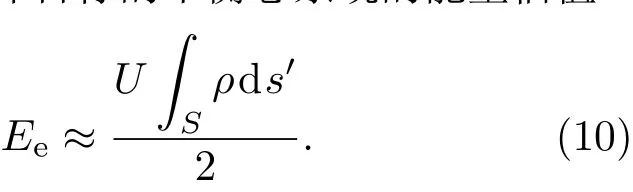
4 结 论

