《反比例的意义》教学设计与思考

浙江温州市仰义第一小学 林志辉 许建云

教学内容：人教版六年级下册第47页内容。

教材分析：

《反比例》是人教版六年级下册“比例”单元第五课时内容。通过对正比例与反比例知识的学习，可以加深学生对比例的理解及对数量关系的认识，初步渗透函数思想，为今后学习中学数学打下基础。

新课程标准的要求是通过具体情境，与学生的生活结合起来，淡化脱离现实背景判断比例关系。认识成反比例的量，能找出在生活中成反比例的实例，并进行交流。显然，理解反比例的意义，判断两个量是否成反比例是本课的教学目标，也是本课的重难点。

教学目标：

1.在具体情境中，理解反比例的意义，并能判断两种量是否成反比例关系。

2.经历对比归纳、抽象模型的学习过程，积累数学活动经验，初步渗透函数思想。

3.在自主探索与合作交流中获得积极的数学学习情感体验。

教学过程：

一、复习引入，揭示课题

1．对比分类

师出示“前测学习单”中的4张表格：

A.用60元购买笔记本，笔记本的单价和数量如下表:

单价（元/本）数量（本）1.5 40 2 3 4 5 6 30 20 15 12 10… …

B.用60元购买笔记本，已花的钱和剩下的钱情况如下表:

已花的钱剩下的钱10 50 15 45 20 40 30 30 40 20… …

C.一辆车以同样的速度前行，行驶的路程和时间如下表：

时间（时）路程（千米）1 2 3 4 5 90 180 270 360 450… …

D.小明读完一本书，平均每天看的页数和看完全书所需天数情况如下表：

平均每天看书的页数看完全书所需的天数10 12 15 8 20 6 30 4 40 3… …

教师出示分类结果（C和A、B、D），提问：谁看明白了它是根据怎样的变化规律来分类的？

学生根据分类结果反推分类标准。

（设计意图：（1）观察表格中的两个量，发现其变化规律，渗透函数思想。（2）给表格分分类，在分类中倒逼学生思考分类的标准，从中解读出增减变化趋势。（3）学习单里的素材贯穿本节课始终，更好体现了结合学生熟悉的具体情境这一教学目标）

2．复习正比例

教师提问：表格C中的两个量之间成什么关系呢？怎样的两个量成正比例关系？

追问：你能想象出它的图像是什么形状吗？教师运用几何画板演示正比例的图像。

（设计意图：结合具体情境，组织学生复习正比例的意义和判断方法。通过学生对原有正比例知识的唤醒，加强解读不变的量、变化趋势、函数图像。通过结合几何画板演示正比例的函数图像，再次感受一增一减的变化趋势）

3．出示课题

师：表C中的两个量成正比例关系，一个量增加，另一个也增加；而表格A、B、D中的两个量，一个量增加，另一个量反而减少，那它们之间成什么关系呢？

学生猜测，教师出示课题：反比例。

二、构建概念理解模型

1．自学反比例

本报讯近日，晋煤金石化工投资集团有限公司成立扭亏脱困项目部，重点推进“系统提取LNG、节能升级改造”等多个项目。

学生带着“如何判断两个量是否成反比例关系”这个核心问题进行自学。

2．对比判断

教师组织学生汇报自学情况，判断表A、B、D三张表格中的两个量是否成反比例关系。

（1）立。师：表A中的两个量是否成反比例关系？学生先独立思考，再同桌交流。

师小结：像这样单价增加，数量减少，总价一定，这两个量就成反比例关系。

（2）破。师：表B中，总价也是一定的，都是60元，教师判断这两个量是否成反比例关系，同意的请举手。

预设此时大部分学生先会举手赞同，慢慢地学生存在质疑，然后在辨析中明理。

师小结：已花的钱+剩下的钱=总价（一定），和一定，不是乘积一定，所以不成反比例。

（3）立。师：那我们来观察表D，表中的两个量到底成不成反比例关系呢？

学生回答，落实反比例的判断方法。

小结：每天看的页数×所需天数=总页数（一定），成反比例关系。

（设计意图：在“立—破—立”的过程中，学生构建反比例概念理解模型。在破与立的思维碰撞中激发学生的兴趣，多角度、立体式的感知、触摸反比例的本质）

3．对比归纳

师：通过刚才的学习，你能用自己的话来说说，怎样的两个量成反比例关系？

学生通过对A、B、D三张表格进行对比，用自己的语言概括归纳反比例的意义。

小结：一个量增加，另一个量反而减少，它们的乘积一定，这两个量成反比例关系。用字母表示：xy=k（一定）。

（设计意图：对比三个表格中两个量的变化规律，用自己的话来说一说怎样的两个量成反比例关系。不同的学生有不同的表达形式，可以是具体直观的数据说明，可以是半抽象的增减趋势，还可以是抽象的表达形式，引导学生从直观到抽象，构建反比例的意义）

三、构建函数图像模型

1．出示图1

师：谁能快速地判断表中的两个量成反比例关系？

追问：那成反比例的两个量的图像是什么形状呢？（教师利用几何画板动态演示反比例的图像）

师：当时间是1小时，速度是？

生：240米/小时。

师：当时间是2小时，速度是？

生：120米/小时。

师：当时间是3小时，速度是？

生：80米/小时。

师：时间越来越大，速度？

生：越来越慢。

师：感受到了吗？在变化的过程中有一个量始终保持不变，是哪个量？

生：路程。

师：那你在图像上能找到吗？

生：反比例图像上黄色部分的面积始终是240，保持不变。

师生小结：像这样一个量增加，另一个量减少，而它们的乘积始终保持不变，我们就说这两个量成反比例关系。

图1

（设计意图：反比例的教学都是从具体问题情境入手的，也就是从特殊到一般学习反比例问题，但问题情境千差万别，容易干扰学生的注意力，而反比例的图像表征却始终保持了一致性，对学生理解反比例的本质起着“直击要害”的作用）

2．对比辨析

师：同样都是速度、时间、路程，为什么左边的两个量成反比例关系，而右边的两个量成正比例关系呢？（图2）

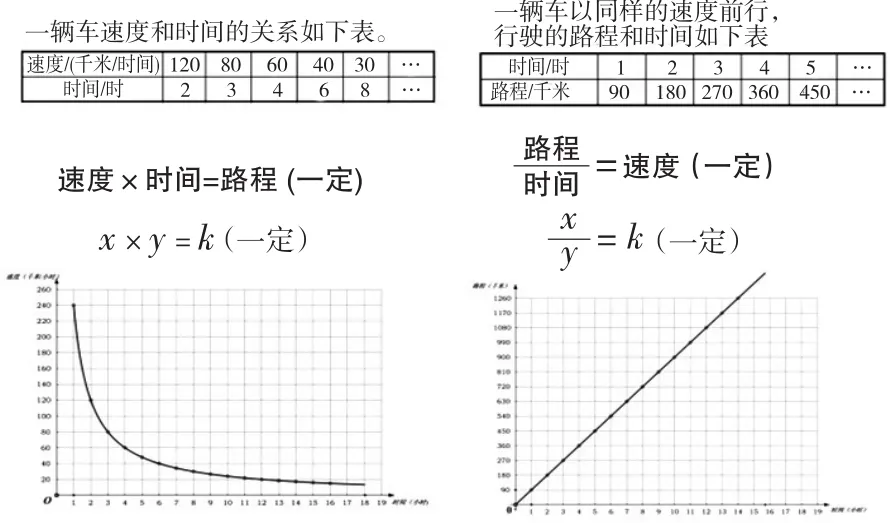
图2

追问 ：那如果时间一定，路程和速度之间成什么比例？

（设计意图：结合正反比例的表格、图像、数量关系式等，在速度、时间、路程这个具体情境中更深入地去思考正反比例的异同点。在辨析的过程中加深对反比例的意义的理解，掌握判断反比例的方法）

四、构建练习推进模型

1．生活的例子

预设学生举例：大米的总重量一定，每袋大米的重量和袋数成反比例；长方形的面积一定，长和宽成反比例等。

2．拓展提升

判断：下面两个量是否成反比例关系？并说明理由。

A.一个数和它的倒数。（成反比例关系）

B.圆的周长一定，圆的半径和圆周率。（不成比例）

C.房间的面积一定，正方形地砖边长和块数。（不成比例）

学生先手势判断，再说明理由。

师：房间的面积一定，正方形地砖边长和块数，成反比例关系吗？手势判断。

师请判断认为成反比例关系的学生说明理由。

生1：地砖的边长增加，地砖的块数就会减少，房间的面积始终不变，所以地砖的边长和块数成反比例关系。

师：谁不赞成他的观点？

生2：房间的面积一定，应该是地砖的面积×块数=房间的面积，而不是地砖的边长乘块数，所以不成反比例。

生1：假如房间的面积是64平方米，地砖的边长扩大2倍，那么块数就要缩小1/2。

师：刚才这位同学借助表格来说明，那老师就把这个表格拿出来。（师出示表格）

房间的面积一定，正方形地砖边长和块数。

地砖边长/cm所需的块数/块20 400 40 100 50 64 80 25… …

生1：它们不成反比例关系。地砖的边长和块数的乘积不一定。

师：请问哪个量是一定的？

生：房间的面积。

师：房间的面积不变，直接相关联的是哪两个量？

生：地砖的面积和块数。

（师出示表格）

房间的面积一定，正方形地砖面积和块数。

地砖面积/cm2所需的块数/块400 400 1600 100 2500 64 6400 25… …

生：实际上地砖的面积和块数成反比例关系。

小结：成反比例关系的两个量，一个量增加，另一个量减少，而这两个量的乘积是一定的。

（设计意图：抛出问题，不局限学生的思维，通过思维的逐层推进，借助抽象的表格再现学生的思维路径，从而提升思维水平，构建练习推进模型）

五、构建课堂教学模型

回顾：今天这节课我们是怎么学习的？

学生静静感受这节课中渗透的数学方法。（对比分类，对比判断，对比归纳，对比辨析）

（设计意图：最后在课堂回顾时，我们着重突出对学习方法的渗透。让学生感受到在整堂课的学习中，始终贯穿着对比分析的研究方法。这样同中求异、异中求同，将对比分析的学习方法从这一课的学习推向一类课的学习，它既是数学课堂教学的一种模型，也是学生学习的一种模型）♪