惯性导航与卫星导航组合定位精度分析及仿真

周 俊，王 琳，徐永强，黄 海，李枭楠

(1.陆军航空兵学院 陆军航空兵研究所，北京 101121；2.中国电子科技集团公司第五十四研究所，河北 石家庄 050081)

0 引言

惯性导航系统(INS)是依据牛顿惯性原理，利用陀螺、加速度计等惯性敏感元件及初始信息来计算载体的姿态、速度和位置[1-2]。惯性导航完全依靠载体自身设备独立自主地进行导航，是一种保密性好且不易受干扰的导航系统[3-4]。但由于惯性器件存在测量误差，这种误差进入导航解算时会随时间累积，导致导航结果的误差随时间发散[5]。

全球卫星导航系统(GNSS)是一种星基无线电导航系统，能为全球陆、海、空、天的各类军民载体提供全天候、全天时和高精度的三维位置、速度和精密时间信息[6-8]。但由于用户接收机在接收其导航定位信号时容易受到遮挡、折射和高动态等因素的干扰，导致信号质量不稳定，进而影响定位精度，甚至失锁[9-10]。而INS与GNSS的组合能够有效地解决惯导误差随时间发散的问题，同时可以增强GNSS接收机对信号的捕获与跟踪性能，提高导航系统的稳定性[11-13]。二者的组合综合了INS稳定性好及GNSS精度高等优点，可以提供高精度且稳定可靠的导航信息，是目前导航领域应用非常广泛的导航模式[14-15]。

本文讨论了应用GNSS信息对INS进行校正的情况，并采用INS与GNSS位置、速度松组合模式，对二者组合导航及GNSS失效后INS单独导航的定位精度进行分析与仿真。

1 INS的误差分析

INS的导航误差是由器件测量误差、初始信息误差和算法精度误差等产生的。其中，惯性器件是INS的核心，其测量精度直接决定着INS的导航性能。惯性器件的测量误差又可以分为确定性误差和随机误差。确定性误差是惯性器件误差的主要部分，包括零偏、安装误差、标度系数非线性误差、温度补偿误差、电压补偿误差、轴向交叉敏感误差、与比力相关误差等。随机误差指由不确定因素引起的随机漂移，一般包括有量化噪声、白噪声、偏差不稳定性、速率斜坡和随机游走等。

惯性器件的确定误差可以通过前期的测试进行标定和补偿，而随机误差只能通过建立适当的误差模型，同时利用外部参考信息进行滤波来估计[16]。

1.1 INS定位误差传播方程

INS的比力方程为：

(1)

选地理系作导航坐标系，当不考虑任何误差时，速度的理想值由式(2)确定[17]：

(2)

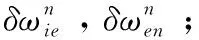
(3)

因重力加速度常作为已知量处理，所以gn′≅gn。

(4)

写成矩阵表达式为：

(5)

式中，RM为卯酉圈曲率半径；RN为子午圈曲率半径；L为纬度；δL为纬度误差；δh为高度误差。

由式(5)可知，INS的测速精度取决于加速度计测量精度、初始位置和速度精度、姿态角精度、解算及模型精度。而姿态角精度又取决于陀螺测量精度、初始信息精度、解算及模型精度。所以，如果初始信息误差为0，解算及模型误差可以忽略，INS的测速精度是由陀螺和加速度计测量精度共同决定的。

由于INS的位置是由速度积分得到的，可以得到定位误差方程：

(6)

所以，忽略初始信息误差、解算及模型误差，INS的定位精度取决于测速精度，而测速精度取决于陀螺和加速度计的测量精度。

1.2 INS的误差特性仿真

通过以上分析，排除初始信息误差、算法误差及一些可以补偿掉的干扰量后，INS的测速和定位精度是由陀螺和加速度计的测量精度共同决定的。如果忽略坐标转换矩阵误差及有害加速度对加速度测量的影响，且加速度计的测量误差为一固定常值，则定位误差等于加速度计测量误差随时间的二次积分。但实际中，加速度计的测量误差为一统计数值，只能通过仿真的方法对惯性器件误差与定位精度的关系进行观测。

仿真状态为静态。初始位置：东经116°，北纬40°，椭球高100 m；初始速度：三轴都为0 m/s；初始姿态角：三轴都为0°。

首先，为观测加速度计漂移对定位的影响，模拟一组陀螺和加速度计的数据，将陀螺漂移及噪声都置为0，加速度计零偏三轴都是0.001 g，随机噪声三轴都是0.002 g(1σ)，解算频率100 Hz，仿真时间120 s，结果如图1所示。

图1 加速度计测量误差引入的定位误差

在初始信息误差及陀螺测量误差为0的情况下，1 mg的加速度计零偏，在2 min时产生的定位误差为：经度72.2 m，纬度72.2 m，高度72.8 m，三维位置误差125.4 m。

然后，观测陀螺与加速度计都存在测量误差时INS的定位精度。初始信息不变，加速度计读数沿用上面数据，向陀螺数据加入观测误差。其中，加入零偏0.05°/s，随机噪声为(1σ)0.07°/s，解算频率100 Hz，仿真时间120 s，结果如图2所示。

图2 加速度计和陀螺观测误差引入的定位误差

在初始信息误差为0的条件下，应用上述精度的陀螺和加速度计数据进行导航解算，2 min时的定位误差为：经度-2 347.8 m，纬度误差2 513.5 m，高度误差193 m，三维位置误差3 445 m。由此可见，陀螺和加速度计的测量误差都会反映到定位误差上，导致定位误差随时间发散。

2 INS与GNSS组合导航的误差分析与仿真

这里采用的是INS与GNSS位置、速度松组合模式。首先建立INS位置、速度及姿态误差模型，并应用GNSS的位置和速度作为校验信息，对INS的误差进行Kalman滤波。然后将滤波结果作为反馈信息对INS的惯性器件误差及定位解算结果进行校正[18-19]。

应用的Kalman滤波模型如图3所示。

图3 Kalman滤波离散滤波方程计算流程

P为系统均方误差阵，

初始值

P0= diag[0.120.120.120.120.120.12102102

1020.0720.0720.0720.00220.00220.0022]。

Z为量测矩阵：

即INS与BDS的速度和位置之差。

H为量测噪声矩阵，Φk，k-1为k-1时刻到k时刻的系统状态转移矩阵：

Q为系统噪声矩阵，

Q= diag[0.0320.0320.0320.0320.0320.032

0 0 0]。

引入GNSS定位结果作为校正信息，其经纬高精度分别为：4 m，6 m，8 m，三维精度10.8 m。

同时将上述带陀螺和加速度计测量误差的数据引入仿真模型进行仿真测试，时间120 s，INS解算频率100 Hz，组合滤波频率1 Hz，INS的定位误差如图4所示。

滤波后定位精度为(1σ)：经度3.6 m，纬度5.5 m，高度7.8 m，三维位置精度为10.2 m。由此可见，导航定位2 min时，组合滤波的定位精度比单INS的定位精度有大幅提高，且定位误差不随时间发散。

图4 INS与GNSS组合滤波定位误差

3 结束语

通过以上分析与测试，INS的定位精度取决于惯性器件测量精度、初始信息精度及解算的精度。陀螺和加速度计等惯性器件的误差反应在INS的定位误差上是随时间发散的。INS与GNSS组合导航的松组合模式，是依靠GNSS信息来校正INS的误差。组合系统的定位精度主要取决于GNSS提供的校正信息的精度、INS误差模型建立的准确性及Kalman滤波器参数的设置。一般情况下，组合导航的定位精度优于单系统的定位精度。

通过大量工程性试验，结果表明利用我国自主的北斗导航卫星和以往传统挠性惯导组合取得了良好效果：解决了惯导的自动对准和时间校正问题，无需人员干涉，缩短了飞行作业准备过程，提高了战斗力；利用卫星定位精度高，时间准确，和惯导进行实时组合，大大提高了惯导的定位精度，克服了惯导随工作时间加长精度变差的弊端，大大提高了装备的性价比，实现低价格、高性能；卫星导航和惯导组合提高了定位测速的平滑性，在飞机应用有重大意义。