杂波背景下基于LFMCW雷达的无人机检测性能分析
余 启,饶 彬,罗鹏飞
(国防科技大学 电子信息系统复杂电磁环境效应国家重点实验室,湖南 长沙 410073)
0 引言
近年来无人机蓬勃发展,给经济社会和军事应用带来便利的同时,也带来一系列威胁。无人机本身作为超低空飞行的小型飞行器,具有速度慢、高度低、RCS小等典型的“低小慢”特征[1],目前仍无很好的探测方法。虽然国内外提出了用红外、声学和激光等传感器对无人机进行探测[2-4],但使用条件多受气象和距离等条件限制。
目前主流的无人机探测雷达主要采用调频连续波体制,其中以线性调频连续波(LFMCW)最为常见。这种体制的典型优点是:近似全天候工作能力、近距离高分辨率多目标探测、峰值功率低、距离分辨率高、收发分离不存在近距盲区、具有较宽的多普勒频带、信号处理简单从而使得整个系统非常简洁、体积小和重量轻[5-8],非常便于关键区域布防。例如英国的AUDS系统[9]集成了布莱特A400系列Ku波段电子扫描防空雷达,采用LFMCW波形和多普勒处理技术,能够对8 km范围内RCS为0.01的无人机进行探测和跟踪。
但无人机作为典型的“低小慢”目标,加之无人机使用一般处于复杂的城郊结合地带,具有较强的地物杂波背景(建筑、车辆等),因此使用雷达检测无人机还面临一系列问题:
① 无人机RCS非常小,而FMCW雷达通过FFT处理从差频信号获取距离信息[10],在强地物杂波背景下对距离维检测的影响机理有待分析;
② 无人机的飞行速度不快(尤其是旋翼无人机的飞行速度更慢,一般在30 m/s范围内),探测雷达由于关注空域过低,地物强杂波不可避免地对速度检测产生影响,一方面需要滤除静态地物杂波,另一方面需要分辨和鉴别车辆等类似慢速移动目标。因此,对速度维检测的影响机理有待分析。
本文以LFMCW雷达为研究对象,重点关注地物块状分布杂波(如建筑)对无人机检测的影响机理。
1 LFMCW雷达测量精度理论分析
常规LFMCW雷达的信号处理流程如下:
① 雷达发射高频射频信号;
② 目标回波信号(可能有多个)在传播过程中叠加杂波信号和噪声信号;
③ 在接收机进行限幅、低噪声放大、滤波、近程增益控制、混频等处理,得到中频信号;
④ 对中频信号进行数字采样;
⑤ 在信号处理机进行动目标指示(MTI)、距离维FFT、速度维FFT、CFAR检测和点迹凝聚(测量)等处理;
⑥ 处理结果送往数据处理器进行进一步的跟踪、识别和显示。
发射信号有多种调制方式,主要分为相位调制和频率调制2类。调制的共同目的是将目标的距离和速度信息转化为频移或相移,为后续的信号处理做准备。其中,多普勒处理(如MTI[11]、速度维FFT[12])等处理并不是必须的,依赖于特定应用目的,主要用于抑制地面杂波。例如,高度计、汽车防撞雷达等一般只进行距离维检测。但对于无人机探测而言,由于目标RCS较小,在速度维进行检测是非常必要的。
1.1 差频信号分析
本文选取线性调频连续波(LFMCW)作为雷达发射信号:
st(t)=cos[2π(f0t+Kt2/2)+φ0],0≤t≤T,
(1)
式中,f0,K,φ0,T分别为中心频率、调频斜率、发射初相和扫频周期,调频斜率K=B/T,B为调频带宽。
先考虑单个目标回波的情况,则雷达接收信号为:
sr(t)=Acos{2π[f0(t-τ)+K(t-τ)2/2]+φ0+φ+φr},
(2)
式中,A,τ,φ分别为接收信号幅度、目标延迟时间和目标相位;φr为接收机相移。
式(3)中目标幅度与雷达的发射功率,天线增益、目标RCS和目标距离都有关,即
(3)
在接收机中,将发射信号和接收信号直接混频并滤除2f0分量,得到差频信号为:
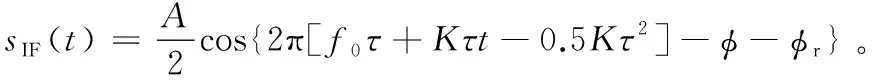
(4)
这里暂不考虑加速度的影响,假定目标是匀速运动的,则目标距离为:
R(t)=R0-vt,
(5)
式中,v,R0分别为目标速度和起始距离。目标时延
(6)
式中,c为光速。将式(6)带入式(4)并整理有:
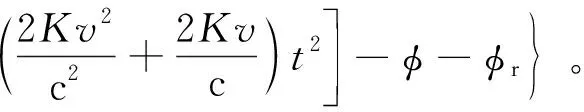
(7)
令
(8)
(9)
(10)
则差频信号化简为:
能源管理平台负责对节能项目进行全过程管理,定期针对项目实施情况进行监督和检查,并对影响该项目节能效果的原因开展分析。
(11)
假设在径向上有L个目标,第i个目标的初始距离为Ri0,初始速度为vi,RCS为σi,相位为φi,目标接收幅度为Ai,多项式系数为ai0,ai1,ai2,则根据线性时不变系统的相关性质,多目标情况下的差频信号为:
(12)
由式(11)可以看出,差频信号本质上是多分量的LFM信号,第i个目标对应的瞬时频率为:
fi(t)=ai1+2ai2t。
(13)
目标距离、速度信息均蕴含于各系数当中(实际上加速度信号也蕴含于其中,阶数更高)。
1.2 测距精度分析
由差频信号公式可知,目标检测问题本质上是多分量LFM信号的参数估计问题,通常是用时频分析的方法来进行参数估计。工程中,由于计算量太大,一般采取简化策略。
注意到目标速度远远小于光速,因此差频信号中c2项在某些情况下可以忽略。单目标情况下差频信号的时频公式为:
(14)
通过整理得到目标距离计算公式为:
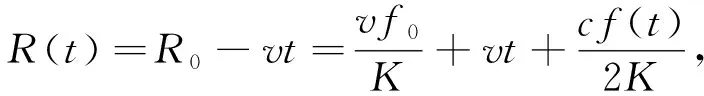
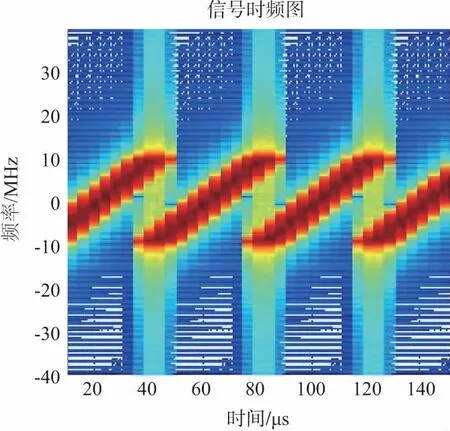
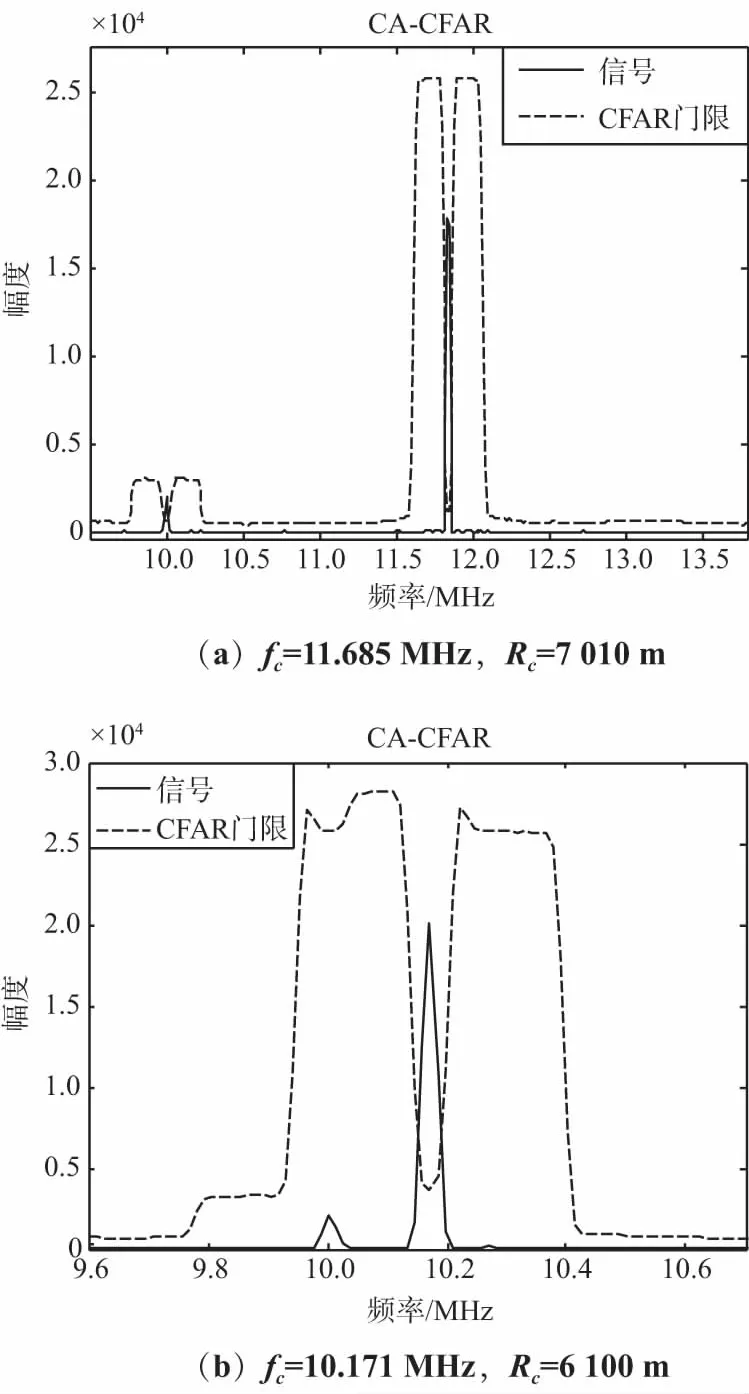
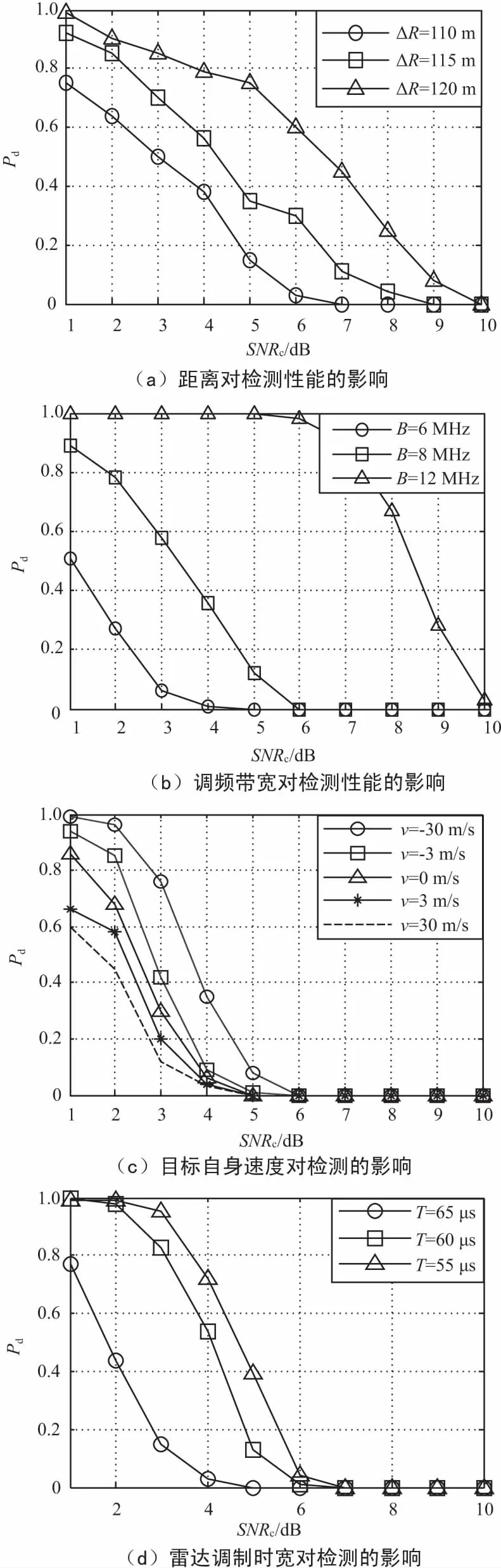
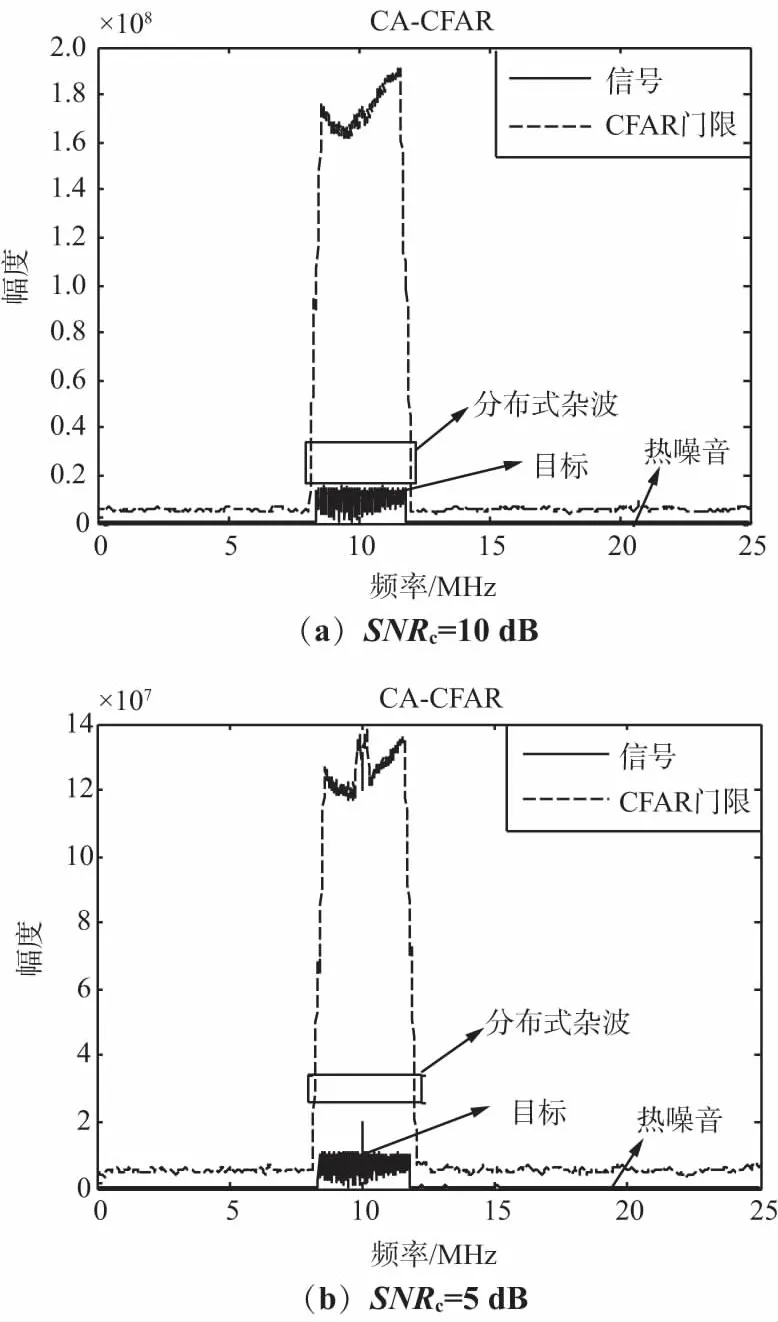
0 (15) 由式(15)可知,目标准确的距离信息实际上是关于目标速度v、载频f0、调频斜率K以及差频频点f(t)的函数,这是动态变化的过程。在实际中,目标测距过程一般在单个调频周期T(ms级之内)内即可完成。在此期间,由于目标速度信息未知,可暂不考虑速度的影响。因此单目标的差频信号近似为单频信号,目标测距公式化简为: (16) 对差频信号SIF的频谱以采样率fs采样M点,得距离计算公式: (17) (18) 下面分析测距精度的影响因素。由式(15)可知距离估计值为: (19) 由于目标速度未知,因此按式(16)测量时速度项带来的实际上是系统误差,频率项是随机误差,因此根据误差传递公式,距离测量误差为: (20) 由式(20)可知,测距精度与目标真实速度值v和测频误差Δf都有关系。理论上,目标速度越小,雷达调频斜率越大,雷达采样频率越高,则测距精度越高。由于无人机本身为慢速目标,因此速度对测距的影响非常小。假设旋翼无人机的速度在0~30 m/s之间,雷达为X波段,带宽为100 MHz,脉宽为10 μs,则速度项带来的误差仅为0.03 m。 下面对差频信号进行频谱分析,同时结合CFAR处理[13],分析邻近块状强杂波对关注目标检测概率的影响机理。 对式(11)进行傅里叶变换: (21) 整理得 (22) (23) 式中,C(u),S(u)为菲舍尔(Fresnel)积分公式, (24) 菲舍尔公式有很好的性质,信号能量主要集中在-a2T/2 (25) 将式(3)和式(9)带入式(25),略去速度项,整理得 a1-a2T/2 (26) 由式(26)可知,目标幅度谱的宽度约为a2T,由于a2项非常小,因此通常近似认为差频信号为单频信号,但实际上是宽度极窄的线性调频信号。幅度谱与目标的RCS(σ)和目标距离R以及雷达参数都是有关系的。 杂波类型有很多种,为简化分析,假定杂波幅度为瑞利分布,速度上有一定的谱宽[15]。这里主要考虑分布式的块状建筑杂波,速度近似为0,但RCS远远强于所关注的无人机,且假设杂波占据连续几个距离分辨单元。 从本质上讲,单个距离单元的杂波可当成单个静止目标来分析。设杂波占据L个单元,第i个单元的初始距离为Ri0,初始速度为vi,RCS为σi,σi为瑞利分布,多项式系数为ai0,ai1,ai2,则根据式(26),杂波的频谱近似为: (27) 根据式(27)可知块状杂波的差频频谱将占距连续几个距离单元,各个频点的峰值与该单元的杂波幅度是呈正比关系的。 下面分析杂波背景下关注目标在距离维的检测概率。与常规脉冲雷达不同,LFMCW雷达的CFAR检测是在频域对幅度检测,差频信号的频谱为目标、杂波和噪声信号频谱叠加,即 |S(f)|=|ST(f)+SC(f)+SN(f)|, (28) 为了进一步降低邻近噪声的影响,工程中一般用恒虚警检测(CA-CFAR)方法[16]来进行检测。当2个目标距离上较近时,频率也会较近,大目标(例如杂波)会影响小目标的距离检测。在这种情况下需要从理论上分析关注目标的检测概率。 以CA-CFAR为例[17],采用平方律检测,假设有N个参考单元,检测单元记为Y,噪声功率水平记为: (29) (30) (31) 设定基本的仿真参数为:雷达调频带宽B=20 MHz,脉宽T=80 μs,综合损耗L=10 dB,中心频率f0=10 GHz,CFAR检测单元N=32,恒虚警概率Pfa=10-6,雷达的脉宽和带宽可设;目标参数为v0=25 m/s,SNR0=10 dB,R0=6 km;杂波参数为vc=0 m/s,SNRc=10 dB,杂波的距离和幅度可设。 根据上面的仿真参数进行仿真实验,产生的LFMCW信号时频图如图1所示,可以看到明显的锯齿调频特征。 图1 差频信号时频图 目标加杂波情况下得到的差频信号频谱图如图2所示。图2(a)、图2(b)具有相同条件f0=10 MHz,R0=6 000 m,A0=1,A1=5。其中图2(a)是两目标相距较远时的差频频谱及CFAR检测结果,由于距离较远(ΔR=1 010 m),频谱能较好地分开,CFAR能成功检测2个目标。图2(b)是两目标相距较近时的差频频谱及CFAR检测结果,由于距离较近(ΔR=100 m),频谱不能较好地分开,CFAR不能成功检测两个目标。由此说明,距离较近时,邻近目标会降低关注目标的检测概率。 图2 对多目标距离维的检测 下面进行100次蒙特卡洛仿真,分析影响检测性能的关键因素。不同参数下检测概率变化曲线如图3所示。 图3 不同参数下检测概率变化曲线 图3(a)为固定其他参数,改变相对距离,得到检测概率随杂波信噪比的变化曲线。由图可知,杂波的信噪比越高,离关注目标越近,则关注目标的检测概率越低。图3(b) 为固定其他参数,改变调频带宽,得到检测概率随杂波信噪比的变化曲线。由图可知,雷达调频带宽越小,关注目标的检测概率越低。实际上,带宽决定分辨率,由式(20)可知,带宽越小,调频斜率越小,距离分辨率下降,测距精度变差。2个目标的差频频点更容易合并,不利于检测。图3(c)为固定其他参数,改变目标速度,得到检测概率随信噪比的变化曲线。由图可知,目标速度的正负值对检测有较大影响。速度的影响表现在差频频点的轻微频移,频移方向与速度正负有关,当朝向邻近强杂波点飞近时,会导致自身检测概率的下降,而当远离杂波点时,自身检测概率又有所提高。 总体而言,由于关注的为旋翼无人机,自身速度的影响并不是太大,在30 m/s的条件下对检测概率大概有20%的影响范围。 图3(d)为固定其他条件,改变扫频周期,得到检测概率随杂波信噪比的变化曲线。分析同前面一致,扫频周期越长,对应调频斜率的下降,反而会造成无人机检测性能的下降。为了便于比较,上面的分析只考虑了单个目标和单个杂波的情况下。实际中,强杂波一般占据连续多个单元,且幅度远远强于热噪声,甚至大于目标的幅度。如果考虑地面车辆、天气等因素的影响,杂波还将具有一定的谱宽。如果目标确实和杂波在距离上重叠,此时的距离测量和距离检测是不准的。分布式强杂波情况下目标的检测情况如图4所示。 图4(a)、图4(b)在相同条件:SNRc=10 dB,R0=6 000 m,Rc在[5 000~7 000]m范围内,图4(a)为目标和杂波的信噪比均为10 dB时,目标在6 000 m处,分布式杂波在[5 000~7 000]m范围内,杂波占据100个单元,杂波谱宽333 Hz,可以看到此时目标已经淹没在杂波中,很难检测出来;图4(b)为目标的信噪比为10 dB、杂波的信噪比为5 dB时,目标在6 000 m处,可以看到此时由于目标的幅度略大于杂波,差频信号上看虽然目标有频谱峰值,但受杂波抬高参考门限的影响,目标仍然无法检测。对于图4的情况,更符合实际场景,此时需要利用速度维的长时间积累,并在速度维进行检测才可以区分无人机和杂波,并进一步进行跟踪和识别。 图4 分布式强杂波情况下目标的检测情况 综合上面的分析,从有利于无人机检测的角度看,在相同情况下,两目标的相对距离越大,检测概率越高;调频带宽越宽,检测概率越高;目标朝远离杂波的方向飞,检测概率越高;扫频周期越小,检测概率越高。因此,为了实现无人机距离维的有效检测,要求雷达的设计采用大的调频斜率和较高的采样率。 无人机检测本身具有“发现难”、“跟踪难”和“识别难”等诸多问题。本文在距离维进行了分析,得出了一些有意义的结论。仿真时主要依据信噪比进行分析。下一步将结合无人机电磁计算或暗室测量结果,并结合杂波具体测量数据具体进行分析。实际上,仅在距离维检测无人机是不够的,地面无人机的飞行速度不快,探测雷达由于关注空域过低,地物强杂波不可避免地也会对速度检测产生影响,一方面需要滤除静态地物杂波,另外一方面需要分辨和鉴别车辆等类似慢速移动目标,下一步还需进行深入研究。
2 LFMCW雷达对无人机检测概率理论分析
2.1 目标差频信号频域分析

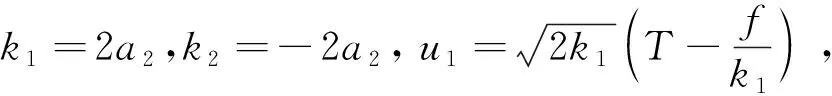
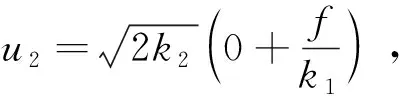
2.2 杂波差频信号频域分析
2.3 目标CFAR检测概率分析
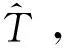
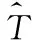
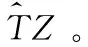
3 仿真实验
3.1 场景描述
3.2 仿真结果
4 结束语

