应用分布目标的极化SAR定标技术研究进展

贺雨露，代大海，赵艳丽，吴 昊，廖 斌

(1.国防科技大学 电子信息系统复杂电磁环境效应国家重点实验室，湖南 长沙 410073；2.国防科技大学 电子科学学院，湖南 长沙 410073；3.中国洛阳电子装备试验中心，河南 洛阳 471003)

0 引言

目标极化信息对揭示目标电磁散射机理、提升极化SAR对目标的分类识别能力以及改善极化SAR对杂波和干扰的抑制能力具有显著作用。G.Sinclair[1]提出将目标的极化散射特性用一个二阶复矩阵来描述，即极化散射矩阵(Polarization Scattering Matrix，PSM)。PSM能够直观且全面地描述目标电磁散射特性，但是由于收发天线、传播环境和噪声等引入的误差，PSM的测量会出现失真。要想应用正确的目标极化信息，定标是一个必要的预处理步骤[2，3]。极化定标求解误差模型和参数，将已失真的测量PSM尽可能地还原成真实的PSM，保障极化SAR测量的可重复性。

在利用分布目标进行极化定标之前，点目标极化定标技术被大量研究，其通过布置已知PSM的人造点目标并对比实际测量的PSM求解误差参数。然而由于误差参数是目标与雷达视角的函数，为了定标一幅SAR图像，需在测绘带内布置大量人造点目标，成本过大，并不实用，本文仅研究应用分布目标的极化定标技术。

本文按SAR载体不同分为机载和星载分开阐述，将定标算法中对雷达系统和目标统计散射特性等做的假设条件作为文章推进的线索，梳理了极化SAR定标从开始基于分布式目标进行定标以来的学术成果，并分析了主流极化定标算法的区别与本质联系，并对极化SAR未来可研究方向进行预测。

1 机载SAR定标

机载SAR比星载SAR受限制条件少，更容易实现，更具灵活性，容易采用、试验新技术，并能得到及时维护；星载SAR所采用的技术，一般先在机载SAR上验证。因此，本文着重讨论分析机载SAR定标技术。

1.1 机载SAR定标误差模型

对于机载SAR，PSM的误差模型为：

M=RST+N，

(1)

(2)

(3)

f1和f2表示极化通道增益不平衡；δ1，δ2，δ3，δ4表示交叉极化方向上的串扰。极化定标只关心矩阵元素间的相对值，忽略复数比例因子，极化定标算法需估计误差参数f1，f2，δ1，δ2，δ3，δ4的值，通过计算

S=R-1(M-N)T-1，

(4)

实现极化定标。

1.2 机载SAR极化定标算法发展历程

学者们从研究点目标定标技术转向研究分布式目标，可以认为是Boregeaud于1987年发表的文献[4]后开始的。Boregeaud的研究表明，当散射体在方位向呈现各项同性分布且地面坡度为零时，交叉极化项和共极化项散射不相关，这一结论简化了分布目标的极化协方差矩阵的形式，成为后来很多学者为进行极化定标而对分布目标做的假设，也称分布目标的方位对称性假设[5]。极化协方差矩阵是目标的二阶极化散射统计特性，下面给出定义：

首先将PSM表示成向量的形式，将下标HH，HV，VH，VV分别用数字1，2，3，4表示，忽略噪声，可得

(5)

(6)

式中，Cs表示真实极化协方差矩阵，上标“H”表示矩阵的共轭转置。

基于分布式目标的定标算法从目标的极化协方差矩阵出发，求解误差参数。

按照论文刊登的时间顺序，最早应用分布目标对机载SAR定标的是美国麻省理工学院林肯实验室的Barnes[6]，在Barnes的定标算法中对分布目标和雷达系统做了如下假设：

① 目标散射具有互易性质，即S2=S3；

③ 雷达系统交叉极化方向上的串扰为0，即δ1=δ2=δ3=δ4=0。

其中，“*”表示复数的共轭。Barnes用分布目标的雷达回波加上三面角反射器的回波完成对通道不平衡参数f1和f2的估计，这种分布目标加角反的组合模式是之后大多数机载SAR定标采用的模式。相比于通过在测绘带内布置大量定标体的点目标定标技术，Barnes的算法绝对是个创新，但是串扰的估计是极化SAR定标的一个重要环节，直接将串扰假设为0限制了这个算法的使用。Barnes的算法不知名也没有太多的实际应用。

美国喷气推进实验室的Van Zyl[7]提出的算法较为知名，之后很多学者对Van Zyl的算法进行研究和改进，Van Zyl保留了Barnes算法的前2个假设，并做如下假设：

④ 雷达系统是互易的，也就是说误差矩阵R是T的转置，结合假设①，测量PSM即M必须是对称阵，所以定标前需对M进行对称化处理；

⑤ 极化串扰足够小，可以忽略其二次项，使误差参数的求解线性化。

VanZyl将自己的算法应用于某沙漠熔岩流区域，通过区域内三角面反射器在定标前后的极化特征图与理想情况下做对比来验证算法的有效性，证明L波段和C波段都有着很好的一致性。对比Barnes算法，Van Zyl对极化串扰做了估计，但是雷达系统互易性的假设显然过于严格，大多数时候是不成立的。

Freeman[8]在分析Van Zyl算法缺陷的基础上，提出了改进的定标算法，将交叉极化数据的加权平均引入到对测量PSM的对称化操作中，拓宽了Van Zyl算法的适用范围。

Klein[9]和Quegan[10]去掉了Van Zyl算法中较为严格的雷达系统互易性假设，Klein采用的是迭代算法，定标结果较为准确，但存在收敛速度慢等问题，而Quegan则是非迭代算法，简单易操作，但非迭代算法也意味着它的误差参数求解不是最优的。

由于分布目标方位对称性的假设有些情况下并不成立，如果极化交叉极化项非常小，以上算法都会失败。Anisworth[11]提出的算法则去掉了方位对称性的假设。然而邢世其[12]提出Anisworth算法存在严重缺陷，该方法得到的误差参数之间存在确定性的关系，Anisworth算法对误差参数的估计不可信。

以上应用分布目标的定标技术的整体思想都差不多，对分布目标极化散射特性做出假设，利用分布目标加上角反射器的回波数据，求解误差参数。但是有很多地形地貌不允许布置角反射器，也有学者试图完全用分布目标进行定标。这类算法的主要特征是定标区域均匀同质，可直接测量或通过其他方式获取其真实极化散射特性。

Sarabandi[13]使用极化散射仪直接测量均匀同质区域的真实极化协方差矩阵，然后对比该区域的测量极化协方差矩阵求解误差参数。此方法的极化散射仪测量时间需和雷达照射时间相近，而且只适合于均匀同质或者近似均匀同质的区域，实用性不足。

Xiong[14]和Sarabandi的条件相同，不同的是Sarabandi在解方程时使用的是代数算法，Xiong则是应用遗传算法来寻求误差参数的最优解。

Mura[15]仅假设散射互异性，利用的是SAR成像前的多视处理子图像和观测协方差矩阵，通过迭代估计全部误差参数，不需要额外布置定标体，但是多视处理方法现在已很少使用。

1.3 机载SAR极化定标算法分析

以Van Zyl[7]，Klein[9]，Quegan[10]，Anisworth[11]等人为代表，通过挖掘分布式目标的极化散射统计特性，建立约束方程求解误差参数，这是研究的主流，且已广泛应用于机载SAR系统的极化定标中，对Van Zyl 等人定标算法的分析很有必要。

算法均假设目标散射互易，即S2=S3。整理式(6)具体到极化协方差矩阵每个元素，

(7)

测量极化协方差矩阵是Hermite矩阵，有10个独立的测量值可组成10个方程。定义一组新的参数：u=δ1，w=δ2/f1，z=δ3，v=δ4/f2，k=1/f1，α=f1/f2，D矩阵可分解为：

(8)

可以看出KCsK和Cs矩阵元素形式相同，所以对真实极化协方差矩阵Cs的形式做假设来设计极化定标算法无法估计k的值，需在测绘带内额外布置定标体。

此类方程试图用10个测量值(C11，C12，C13，C14，C22，C23，C24，C33，C34，C44)形成方程组解5个SAR系统误差参数(u，w，z，v，α)和6个分布目标参数(S11，S12，S14，S22，S24，S44)。Van Zyl，Klein，Quegan假设方位对称性：

S12=S24=0。

(9)

VanZyl另外还假设雷达系统互易，对测量PSM做对称化处理后，有以下假设条件：

(10)

实际上是用6个方程组解2个误差参数和4个未知数，方程的解可求且唯一。

Klein和Quegan则是用10个方程解5个误差参数和4个目标参数，通过列出方程组发现α的求解是超定的。Klein应用了矩阵的瑞利熵性质，用极化协方差矩阵的特征向量元素的值估计出α的值。Quegan则是加入了另一未知数噪声N22=N33来解方程组，Kimura[16]认为N22和N33的值并不一定相等，改进成用m=N22/N33来解方程组，m的值可由对目标RCS较低的区域测量获得。

Anisworth不做方位对称性的假设，没有减少未知数个数，需用10个等式解5个误差参数和6个未知数，理论上是不可行的。邢世其提出其每一次迭代，参数之间存在确定性关系，例如第i次迭代，

ui=-αizi，

(11)

vi=-wiαi。

(12)

方位对称性的假设也可以应用于Anisworth的算法，只需每次迭代时，将对C12和C13取平均值改成等于0即可，C24和C34也是如此，这个时候参数没有式(11)和式(12)的约束关系。

这类定标算法通过增加假设来减少求解误差参数的值，原理较简单易理解。如果假设条件过少，定标算法便会出现问题。在分布目标不满足方位对称性假设的情况下，如何对目标极化测量数据进行定标仍然是需要解决的问题。

2 星载SAR定标

星载SAR的PSM误差模型可以表示为：

M=RFSFT+N。

(13)

对比机载SAR定标模型，矩阵F为：

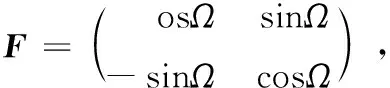
(14)

是由法拉第旋转引入的误差矩阵：从轨道飞行器发射的雷达电磁波穿过电离层照射到地表，经地表散射又穿过电离层回到雷达，此时线极化电磁波将会发生极化旋转，称为法拉第旋转。Ω为旋转角度，其值与电磁波频率的平方成反比，频率较低的雷达受到的影响较大，其值还与地球磁场的方向有关[17]。

如果Ω小到可以忽略不计时，如对靠近赤道区域的定标，机载SAR的定标算法也可以直接应用到星载SAR定标中。2009年Touzi[18]对PALSAR在亚马逊地区的极化测量数据进行定标，由于亚马逊地区位于赤道附近，法拉第旋转角度忽略不计，采用的是Freeman对Van Zyl的改进算法[8]。2015年Moriyama[19]对PALSAR2在亚马逊地区的极化测量数据进行定标，采用Quegan[10]算法。Touzi和Moriyama均证明了亚马逊地区适合星载SAR对雷达接收和发射系统的定标，而高纬度的极化定标会受到Ω的影响。

由于法拉第效应包含了线极化的旋转，其主要的影响就是在PSM的共极化和交叉极化项之间额外增加了相关性。如果Ω无法忽略不计，但是仍采用机载SAR定标算法，法拉第旋转效应会被估计成天线中的串扰项加以消除，定标结果则会存在较大误差[20]。

考虑法拉第旋转效应的星载SAR定标研究主要分为2类：一类是认为雷达发射和接收系统无需校准且噪声不存在的理想条件下，或者是系统已经经过定标的情况下，总之是只考虑法拉第旋转的效应，则定标模型(13)可简化为：

M=FSF。

(15)

定标模型的参数较少，比较简单，文献[21-24]分别给出Ω值的估计，文献[25]对这几种估计进行了总结和比较。由于收发系统误差是重要的定标部分，自然不能忽略，此类对Ω的估计器实用性不够。

另一类则是考虑系统失真的定标，Freeman[26]假设串扰忽略不计(<-30 dB)，通道不平衡参数可以通过预先的测量求解，通过上一类中的估计器估计Ω。显然，此算法没有估计串扰值，不平衡参数也不能立即求解。

Freeman[27]又尝试对星载SAR的极化串扰进行定标，假设Ω较小(cosΩ=1，sinΩ=Ω)，分为2种讨论如下：

① 极化串扰值忽略不计，Freeman证明这种情况下的星载SAR极化定标与Quegan[10]算法没有区别；

② 增加假设：串扰互易(δ1=δ3，δ2=δ4)，可估计所有误差参数且无须布置定标体。

研究表明现代天线阵列的串扰不能认为是互易的，且在太阳活跃期，75%的L波段卫星轨道的Ω角度大于5°，所以此方法在实际应用方面还是有所限制。

文献[28]基于统计最优协方差匹配的数值方法，利用分布式目标和角反射器的测量数据共同估计系统误差和法拉第旋转。同样是数值优化器，文献[29]应用的是遗传算法，但是相对于文献[28]，其不需要方位对称性的假设。

NASA JPL实验室已成功使用Quegan[10]算法在机载和星载SAR系统极化定标测量中进行了实测验证。实际上忽略法拉第旋转效应，星载SAR系统硬件性能良好，现如今很多极化测量数据直接应用而并不进行定标工作，更多时候关注机载SAR极化定标的研究结果。

3 结束语

极化定标已经有近30年的历史，但仍存在不少问题。首先学者们在提出算法时会用实验或仿真验证自己的算法，多是用已知点目标的PSM来进行验证，实际上存在偶然性，整个图像定标效果较差，但场景中用于验证的角反射器或其他点目标的定标效果较好的情况是存在的。

大多数定标算法都没有考虑到噪声的影响。为了得到更精确的极化信息，研究雷达的噪声来源、类型和在不同波段、环境下对极化信息获取的影响，然后对此进行针对型定标是个值得研究的问题。

极化SAR定标技术是伴随着极化SAR的发展而发展的，新型极化SAR的发展则会衍生出定标的需求。一般来说，极化SAR系统包含双极化和全极化2种模式，除这2种之外，最近紧缩型极化以更简单的系统、更低的数据率和更宽的带宽得到了不少的关注，特点是仅发送一种极化方式的电磁波，以2种正交极化方式接收，是双极化和全极化的折中。文献[30]中应用分布目标对3种紧缩型极化方式的定标做了分析，学者可以试图对其算法进行改进。

随着技术的发展，除了传统的机载、星载平台，弹载、地基SAR、无人机SAR、临近空间平台SAR和手持式设备等多种形式平台搭载的SAR等也正广泛用于军事、民用领域，如果需要获取精确极化散射信息，如何对它们进行极化定标也是需要解决的问题。