基于KPCA的图像压缩方法

蔡 楠，李 萍

(宁夏大学 物理与电子电气工程学院，宁夏 银川 750021)

0 引言

图像压缩是图像存储、处理和传输的基础，可以减轻图像存储和传输的负担，使图像在网络上实现快速传输和实时处理。图像具有庞大的数据量，在面对高维数据的处理中往往使得图像所包含的有用信息得不到有效的挖掘、提取和利用，因此有必要对图像数据进行压缩。

在图像压缩领域中存在大量的算法，其中文献[1]在介绍了基于DCT的图像压缩编码基础上对一种新的DCT系数分层传输的方法进行研究，通过分层压缩达到了较好的峰值信噪比；文献[2]提出了JPEG-HVS算法通过CSF生成了新的量化表，达到了高压缩比并且解码质量更好；文献[3]采用多级小波变换提高了图像压缩的时间；文献[4]采用主成分分析算法(Principal Component Analysis，PCA)通过提取图像的线性特征达到较好的压缩效果，但是在非线性特征提取上仍有很大的缺陷。为此，本文采用基于核的非线性特征提取算法——核主成分分析算法(Kernel Principal Component Analysis，KPCA)[5-6]。Scholkopf 等人最早将核方法思想应用于特征提取中，于1999年借鉴SVM 的核方法思想，将PCA拓展到非线性情形，提出了核主成分分析[7-8]。KPCA是PCA的改进算法，能够提取非线性特征，可以将原输入空间下线性不可分的数据映射至高维特征空间使其线性可分，从而实现了对非线性特征的提取[9]。通过实验仿真，表明KPCA在继承传统PCA优点的基础上弥补了PCA对非线性特征提取能力差的缺点。

1 KPCA原理

KPCA的基本原理是通过非线性映射φ将输入空间变换到高维特征空间使其线性可分，在高维特征空间下使用PCA完成特征提取[10]。

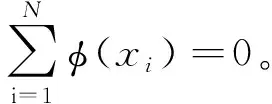
(1)

求协方差矩阵的特征值λ和特征向量α：

λα=Cα。

(2)

K=φ(x)Tφ(x)。

(3)

求出核矩阵的特征值和特征向量：

λkαk=Kαk=φ(x)Tφ(x)αk。

(4)

将式(4)两边同时左乘φ(x)，再将式(1)代入式(4)，令C的特征向量v=φ(x)αk，得

(5)

将v单位化，并将式(3)代入式(5)，得

(6)

将特征空间的样本点φ(x)投影至特征向量v即可得到在主成分上的投影令其为βk，

(7)

2 基于KPCA的图像压缩原理

2.1 KPCA的图像特征降维

基于上述KPCA的原理，将图像中的非线性特征映射至高维特征空间使其线性可分，从而可以将图像中的噪声与主要特征更好地分离达到冗余的去除[15]。具体方法如下：

① 将一幅m×n的图像转为灰度图像后按列分为m×1的n个列向量作为输入样本X；

② 选取核函数，根据式(3)计算核矩阵K，为了防止非线性映射后样本φ(x)不能均值化，需要对核矩阵K归一化后替代原来的核矩阵K[16-17]，再根据式(4)求出特征值λk和特征向量αk；

③ 将λk按从大到小的顺序排列并计算每个特征值占特征值总和的比例和，作为累计贡献率[18]；

④ 根据所设置的累计贡献率大小选取前k个主成分，根据式(7)计算样本在特征空间中主成分上的投影βi(i=1，2，3…k)，即为原图像经KPCA降维后的特征。

2.2 KPCA特征空间原像重构

如何从特征空间中把降维后的特征还原至输入空间，就是KPCA特征空间原像重构。

由于无法确定具体的非线性映射，所以只能近似地求解出特征空间中所对应输入空间的原像，为此期望找到一个向量z∈RN，z=(z1，z2，…zn)T所对应在特征空间下的形式为φ(z)T，使其在重构误差ρ(z)=‖φ(z)T-Pnφ(x)‖2下为最小[19-20]。将ρ(z)展开并把展开后与z无关的表达式均用Ο来代替，并代入式(6)、式(7)得：

(8)

为了重构原输入空间X即需要求出式(8)最小值所对应的z即可，

(9)

3 仿真结果与分析

3.1 实验仿真一

在Windows7环境下使用Python语言调用sklearn中自带的数据集，生成2类半月形分布的点集如图1所示，分别经PCA与KPCA对其进行处理，如图2和图3所示。

通过图2和图3可以看出，对非线性分布的数据经PCA处理后都存在着重叠无法进行有效分离的问题，而经KPCA处理后不存在重叠的问题，可以将非线性数据更好地分离。

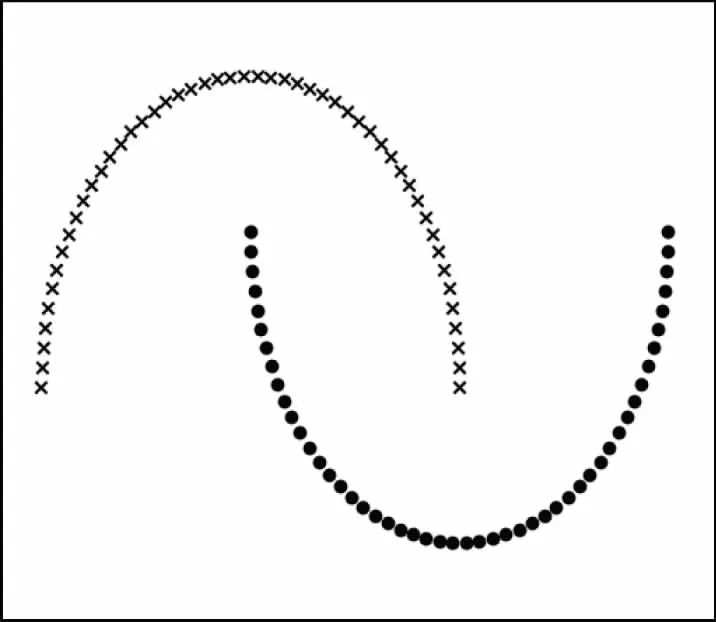
图1 2类半月形分布点集

图2 PCA处理

图3 KPCA处理

3.2 实验仿真二

采用了ORL人脸数据库，从中随机选取312幅图像、取多项式核函数、累计贡献率均设为97%作为特征提取的阈值[21]。通过压缩比(CR)和峰值信噪比(PSNR)分别比较PCA与KPCA对图像的压缩程度和压缩质量，计算公式为：

(10)

(11)

式中，n为原图像的主成分数；k为压缩后图像的主成分数[22]；

式中，I，J分别为原图像与压缩后的图像。仿真结果如表1、图5和图6所示。

表1 PCA与KPCA图像压缩数据

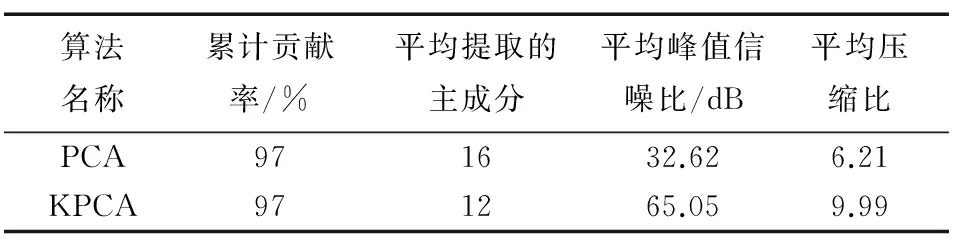
算法名称累计贡献率/%平均提取的主成分平均峰值信噪比/dB平均压缩比PCA971632.626.21KPCA971265.059.99

由表1可以看出累计贡献率均设为97%，KPCA在数据集上平均提取的主成分约为12个，包含了图像97%的特征，相对PCA有着较好的提取能力。在图像压缩质量和压缩程度方面KPCA的平均峰值信噪比比PCA高出了约2倍，压缩比高出了约1.6倍。说明KPCA在压缩质量和压缩程度均优于PCA。

图4为ORL人脸数据库中的3幅原图像；图5为将累计贡献率设为97%作为阈值提取主成分经PCA压缩后的3幅图像，分别提取了11，17，12个主成分；图6为将累计贡献率设为97%作为阈值提取主成分经KPCA压缩后的3幅图像，分别提取了9，15，11个主成分。

图4 ORL人脸数据库原图像

图5 PCA压缩后的图像

图6 KPCA压缩后的图像

由图5和图6可以看出，经KPCA压缩的视觉效果要优于PCA，KPCA在主成分的提取上也少于PCA并有着较高的清晰度。

3.3 实验仿真三

继续采用仿真二中的数据，仍然将累计贡献率设为97%作为KPCA特征提取的阈值，并以CR和PSNR作为参数指标比较JPEG与KPCA对图像压缩的程度和质量，如表2和图7所示。

表2 JPEG与KPCA图像压缩数据

算法名称平均压缩比平均峰值信噪比/dBJPEG9.66732.083KPCA10.03163.962

图7 JPEG压缩后的图像

通过表2可以看出，KPCA在压缩程度上不仅高于JPEG，而且在平均峰值信噪比上也比JPEG高出了2倍，说明KPCA有着更好的压缩性能。

通过图6与图7可以看出，在视觉效果上KPCA也要优于JPEG，说明KPCA压缩的质量更高。

4 结束语

本文研究利用KPCA算法对图像进行压缩过程中提取非线性特征，通过实验仿真一，由于在图像中存在着大量的非线性特征和噪声干扰，KPCA能够将其更好地分开从而降低了图像中的信息冗余达到更好的压缩效果；通过实验仿真二，对比了PCA与KPCA在图像压缩中的性能，结果表明KPCA有着良好的非线性特征提取能力，并且在压缩性能上均优于PCA；实验仿真三比较了KPCA与传统JPEG压缩算法，KPCA不仅在压缩比高于JPEG，而且在压缩质量上也优于JPEG。因此KPCA算法适用于图像压缩，并有着较好的非线性特征提取能力，可以作为图像的预处理器。