三参数隔振系统归一化模型及参数优化

焦小磊， 赵 阳， 马文来, 李思梁

(1. 哈尔滨工业大学 航天学院， 哈尔滨 150001； 2. 中科院 沈阳自动化研究所， 沈阳 110016)

航天器上的执行机构由于制造过程中不可避免的存在一些加工误差，当执行机构正常工作时，会产生一系列幅值小、频率高的微振动，严重影响星上有效载荷的正常工作。国外曾有研究表明，这类执行机构微振动会使卫星上成像设备所拍摄的图像变得模糊。现代航天器正向高精度、高分辨率方向发展，因此，必须对这类微幅振动进行有效隔离。被动型隔振器由于具有较高的可靠性，因此在航天器上的应用比较广泛。

三参数隔振系统由主刚度、附加刚度、阻尼元件组成，相较与传统的两参数模型来说，阻尼元件上串联了一个弹簧，相当于和基础弹性连接，通过合理设计，其在高频段的隔振性能要比传统两参数模型更加优异。

三参数隔振系统又称为弹性连接隔振系统，由并联弹簧，阻尼元件，串联于阻尼元件上的弹簧组成。最早由Ruzicka等[1-2]提出，并对其进行了比较详细的研究。 Yamakawa[3]研究了三参数隔振系统在瞬态激励下的响应，表明其具有较好的缓冲作用。Brennan等[4]研究了刚度以及阻尼对三参数隔振系统性能的影响，他指出，对于简谐激励来说，具有较好的隔振效果。Davis等[5-7]公司研制了一系列基于三参数模型的隔振器，该系列隔振器成功应用于哈勃太空望远镜，经在轨数据表明，其隔振效果非常好，并且具有较高的可靠性。但由于政策原因，该类型隔振器的减阻机理并未公开。国内也有学者对三参数隔振系统作了系统的研究。王杰等[8-9]对基于三参数模型的流体阻尼器进行了研究，给出了三参数隔振器等效参数测试方法。王超新等[10]给出了三参数隔振器最优阻尼设计方法。廖蕾[11]研究了基于三参数模型的波纹管式流体阻尼隔振器的隔振性能。杨庆俊等[12-13]测定了三参数隔振器的线性阻尼系数和平方阻尼系数。何玲等[14-16]研究了摩擦力、流体质量、非线性阻尼力等因素对基于三参数模型的流体阻尼器隔振性能的影响。Liu等[17]研究了基于三参数模型的隔振器对整形隔振性能的影响。

上述研究多集中于物理参数的改变对隔振性能的影响，鲜有对三参数隔振系统进行性能优化设计，而三参数隔振器属于被动型隔振器，共振峰和高频衰减率存在冲突，在实际设计时，必须注意两者的权衡。本文提出基于归一化模型的三参数隔振优化设计方法，针对共振峰和高频衰减率进行多目标优化设计，并给出阶跃激励下，系统性能参数的近似估算方法，仿真算例验证了方法的可行性。

1 三参数隔振器动力学模型

三参数隔振系统由主刚度、附加刚度、阻尼元件组成，主刚度一般由弹性元件来提供，也即系统的静刚度。附加刚度一般由流体压缩时的体积刚度来提供。系统可以用弹簧-质量块模型来描述。模型如图1和图2所示。

图1 三参数隔振系统模型Fig.1 Three parameter isolation system图2 机械阻抗模型Fig.2 Mechanical impedance model

(1)

对式(1)拉氏变换，得到复方程组

(2)

根据复方程组可以较为方便的对三参数隔振系统的时域和频域特性进行分析。

2 模型的归一化

为了便于讨论，将模型转换到复域下，并对模型进行归一化处理。

根据图3可以写出机械阻抗的传递函数

(3)

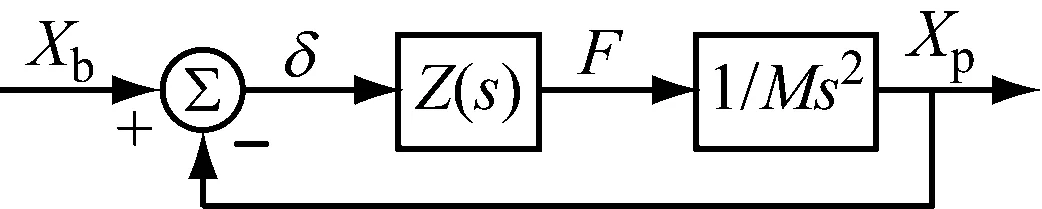
图3 传递函数框图Fig.3 Transfer function block

可以写成下面形式

(4)

图4是系统开环传递函数的Bode图。

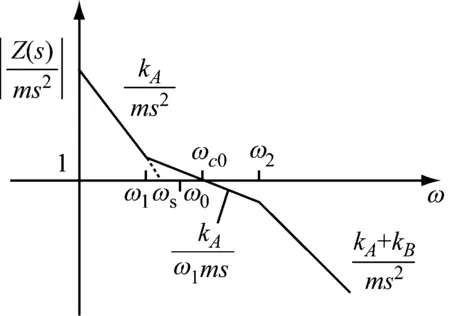
图4 Bode图Fig.4 Bode plot

ω1，ω2是Bode图中转折频率，这里

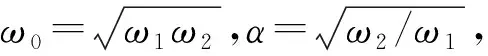
(5)

(6)

可求得

(7)

由KA，KB，CA转换到KA，α，ω0的变换关系为

(8)

由KA，α，ω0转换到KA，KB，CA的变换关系为

(9)

由于临界阻尼可以表示为

定义刚度比N=KB/KA，阻尼比ζ=CA/C0，则N，ζ与α，β的转换关系为

N=α2-1

(10)

(11)

图5是系统阻尼比与无量纲参数α，β的包络面。根据式(8)可以知道，参数α和系统刚度比有关，对于三参数系统来说，刚度比大于零，因此有α>1。当α取值固定时，随着β的增加，系统阻尼比也会增加。同时，若β取值固定，随着α取值增加，系统阻尼比也会增加。图6是系统刚度比与无量纲参数α的关系，刚度比随参数α取值增大而增大。ζ<1时，系统处于欠阻尼状态，ζ>1时，系统处于过阻尼状态，ζ=1时，系统处于临界阻尼状态。

图5 ζ与α，β的关系Fig.5 Relationship for ζ，α，β

固有频率的换算关系为

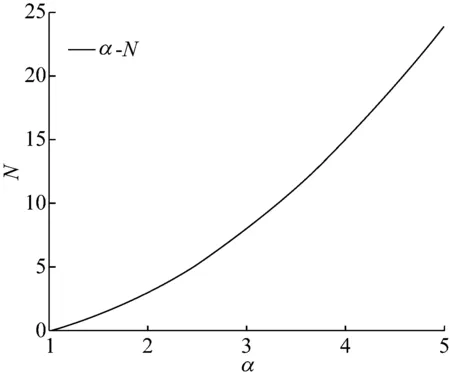
图6 N与α的关系Fig.6 Relationship between N and α

(12)

而当附加刚度为零时，系统固有频率为

可以得到两个固有圆频率之间的关系

(13)

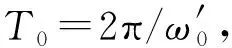
(14)

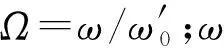
3 隔振系统时域响应分析

这里以单位阶跃激励和正弦激励为例，对隔振系统时域响应进行分析，其中，单位阶跃激励的性能指标可以选择调节时间、峰值时间、超调量。正弦激励的性能指标为共振放大倍数和高频衰减率。

3.1 单位阶跃激励

当外界输入为单位阶跃激励时，系统的传递函数可以写成下面的形式

(15)

式中:S=s/ω0;S1，S2，S3为三个特征根，可以写成下面的形式

S1=c，S2=a+bi，S3=a-bi

通过Laplace逆变换可以得到时域响应

2Veatsinbt)

(16)

p1=ma+1，p2=mb，p3=-4ab2+2cb2

表1给出归一化参数α，β与刚度比N、阻尼比ζ的对应关系。

图7是α=1.2时系统对于单位阶跃激励的时域响应。β取值分别为0.16，1，6.25。可以看到，β=1时，三参数隔振系统对于单位阶跃激励的调节时间要明显小于β=0.16和β=6.25的情形。同时，超调量较其他两种情形也要小一些，时域响应曲线的震荡程度也要明显小于其他两种情形。图8是α=1.5时系统对于单位阶跃激励的时域响应。β取值分别为0.16，1，6.25。同α=1.2时的情形相似，β=1时的调节时间也要明显小于β=0.16和β=6.25的情形。时域响应曲线的震荡程度也要明显小于其他两种情形。α=1.5时的调节时间和超调量也要小于α=2的情形。图9是α=2时系统对于单位阶跃激励的时域响应。β取值分别为0.16，1，6.25。三参数隔振系统对于单位阶跃激励的调节时间要明显小于β=0.16和β=6.25的情形。同时，超调量较其他两种情形也要小一些，时域响应曲线的震荡程度也要明显小于其他两种情形。图9是α=3时系统对于单位阶跃激励的时域响应。β取值分别为0.16，1，6.25。可以看到，β=1时，三参数隔振系统对于单位阶跃激励的调节时间要明显小于β=0.16和β=6.25的情形。同时，超调量较其他两种情形也要小一些，时域响应曲线的震荡程度也要明显小于其他两种情形。α=3时，系统对于单位阶跃激励的调节时间要明显小于α=1.2，α=1.5，α=2时的调节时间。

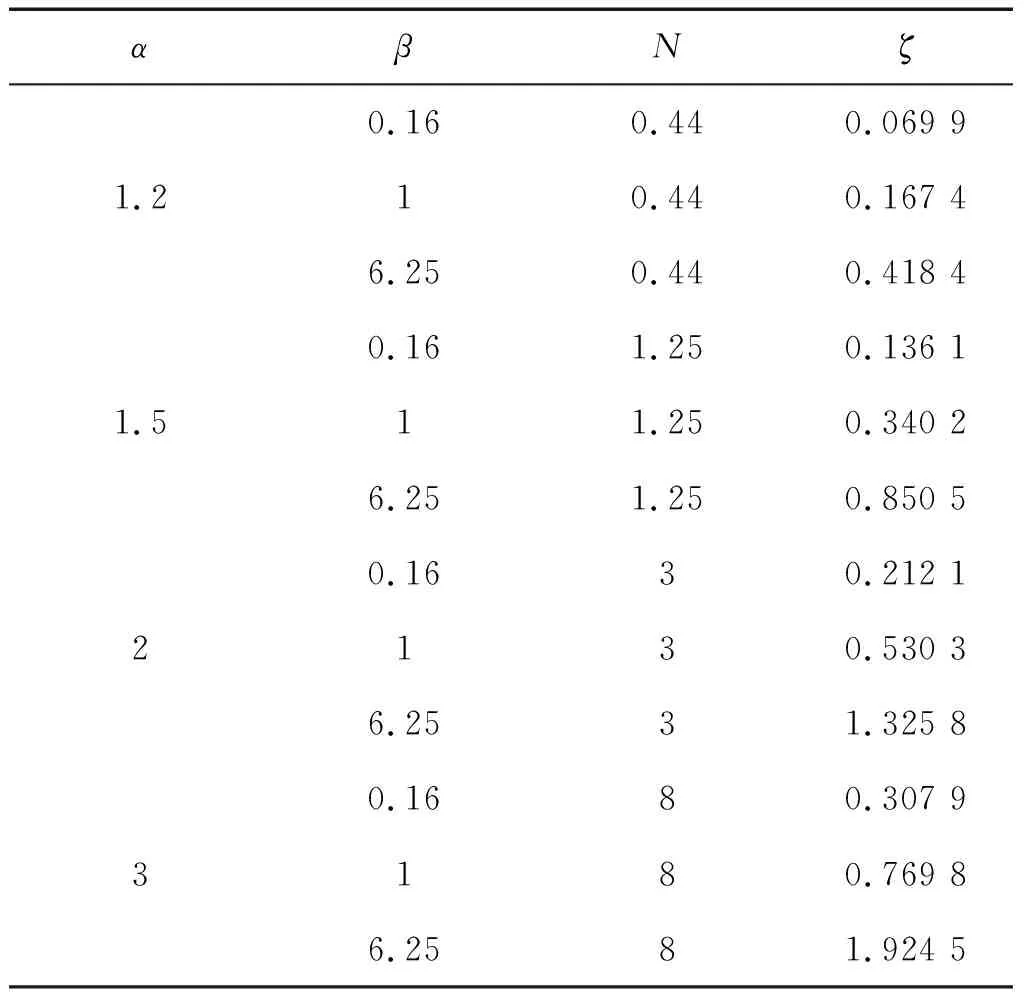
表1 归一化参数和物理参数Tab.1 Normalized parameter and physical parameter

图7 α=1.2时的时域响应Fig.7 Response in the time domain (α=1.2)

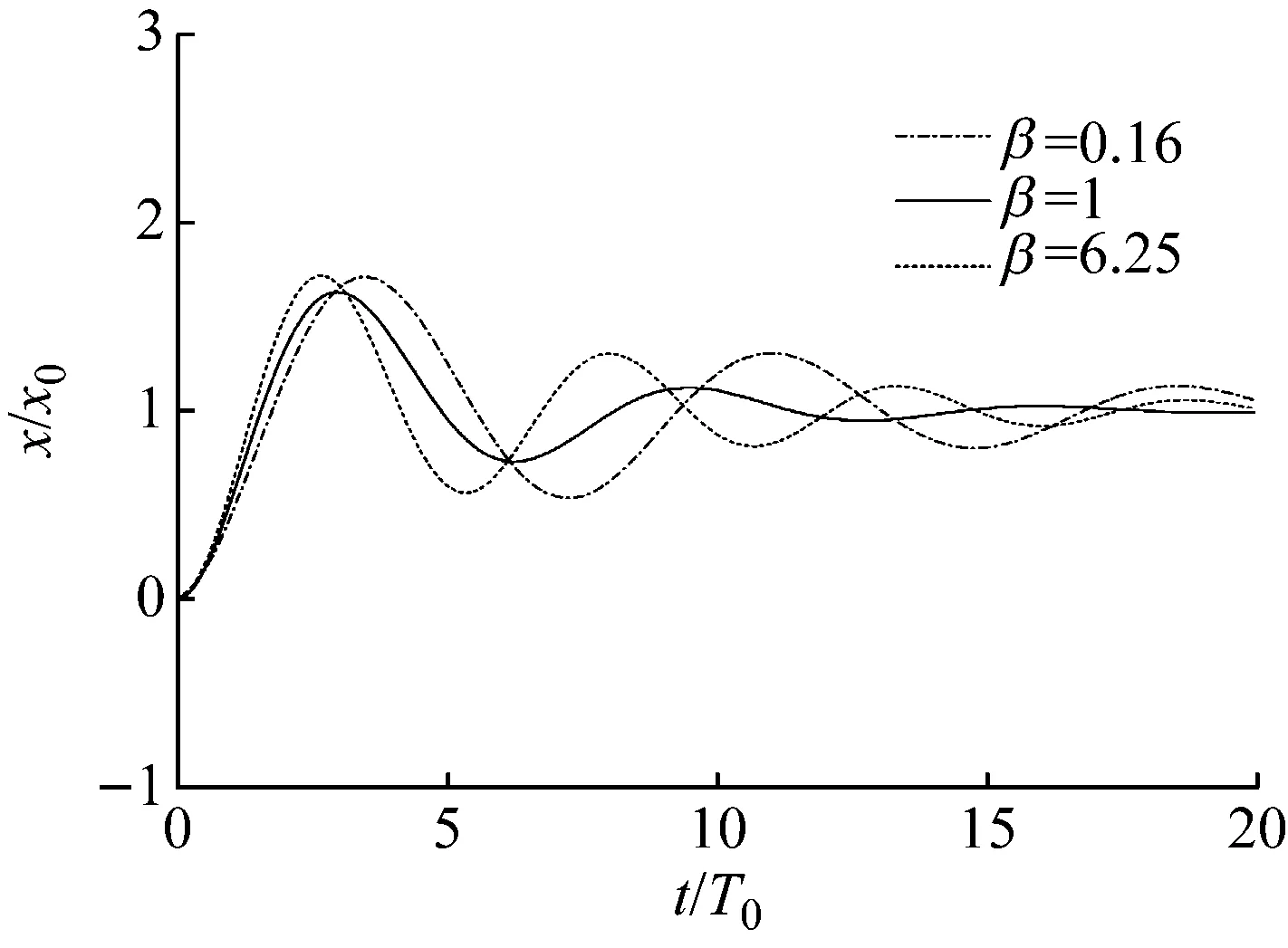
图8 α=1.5时的时域响应Fig.8 Response in the time domain (α=1.5)

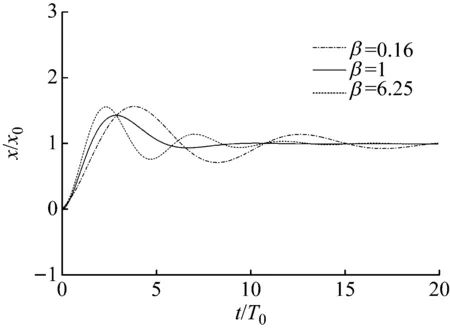
图9 α=2时的时域响应Fig.9 Response in the time domain (α=2)

图10 α=3,β=0.16,1,6.25Fig.10 α=3,β=0.16,1,6.25

表1是归一化参数与物理参数的对应关系。分成4种工况，对应前面的单位阶跃激励的4种工况。α取值分别为1.2，1.5，2，3。每种工况下，β取值分别为0.16，1，6.25。当α取为1.2时，刚度比为0.44，阻尼比均小于1。说明此时系统处于欠阻尼状态，对照图7来看，振荡较为明显。当α取值为1.5时，刚度比为1.25，阻尼比也均小于1，但同α=1.2的情形相比，此时阻尼比明显偏大一些，对照图8可以看到，时域响应曲线振荡要弱一些。当α取值为2时，刚度比为3，β=6.25时，阻尼比大于1，系统此时处于过阻尼状态。当α取值为3时，刚度比为8，相比于前面3种情形，此时时域响应曲线振荡最为平缓，β=6.25时，系统处于过阻尼状态。

3.2 正弦激励

当外界激励为正弦激励时，激励描述为

x=Asinωt

系统的传递函数可以表示为

(17)

式中：S=s/ω0；S1，S2，S3为三个特征根，可以写成下面的形式

S1=c，S2=a+bi，S3=a-bi

通过Laplace逆变换可以得到时域响应

(18)

p1=ma+1，p2=mb，p3=-2b2(a2-b2+ω2)

p4=-4ab3+2b(a-c)(a2-b2+ω2)，p5=1

p6=-mω，p7=-2ω2(a2+b2-ω2)-4acω2

图11～图13是参数根轨迹，β取值分别为0.5，1，1.5， 的取值任意，从图中可以看出，根轨迹有3个分支，分别对应于3个特征根。图11是β取0.5时的根轨迹，此时第1个分支位于实轴上，表示此时系统存在实数特征根，第2个分支有一部分位于实轴的上半平面，表示虚部为正数，还有一部分位于实轴上。第3个分支有一部分位于实轴的下半平面，表示虚部为负数，还有一部分位于实轴上。此外有部分分支位于实轴右侧正数部分，此时系统是不稳定的。图12是当β=1时，第1个分支重合于(-1,0)，第2个分支有部分位于实轴上半平面，表示虚部为正数，还有一部分位于实轴上，第3个分支有一部分位于实轴的下半平面，表示虚部为负数，还有一部分位于实轴上。图13是β取1.5时的根轨迹，此时，第1个分支位于实轴上，表明此时系统存在实数特征根，第2个分支有部分位于实轴上半平面部分，表明虚部为正数，还有一部分位于实轴上，第3个分支有一部分位于实轴下半平面部分，表明虚部为负数，还有一部分位于实轴上。对于3种情形来说，所有位于实轴右侧的根轨迹部分不稳定，同时可以判断右侧部分α<1，对于三参数系统来说刚度比是大于1的，因此右侧部分不符合要求，在设计时应予以舍弃。随着根轨迹向实轴的靠近，阻尼比逐渐增大，位于实轴上的根轨迹达到临界阻尼比。

图11 β=0.5时的根轨迹Fig.11 Root locus for β=0.5

图12 β=1时的根轨迹Fig.12 Root locus for β=1

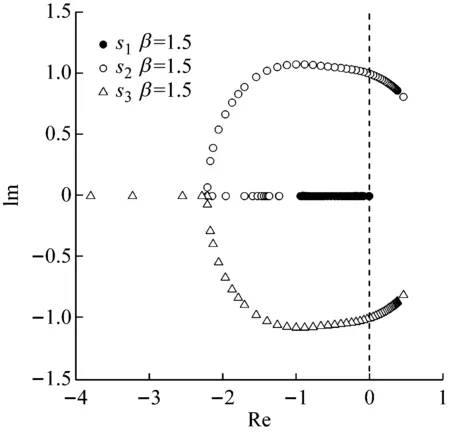
图13 β=1.5时的根轨迹Fig.13 Root locus for β=1.5

4 参数优化

4.1 正弦激励下的参数优化

针对正弦激励来说，由于被动型隔振系统的共振峰和高频衰减率存在一定的冲突性，为了同时满足两种指标的要求，需要进行多目标优化。 优化方法采用带精英策略的快速非支配排序遗传算法(NSGA-Ⅱ)。

NSGA-II(带精英策略的非支配排序遗传算法)运行效率高，解集具有良好的分布性，特别对于低维优化问题具有较好的表现，是应用最为广泛也是最成功的多目标优化算法之一。程序流程如图14所示。图15是优化流程图。

图14 NSGA-Ⅱ算法流程图Fig.14 Program flow chart for NSGA-Ⅱ

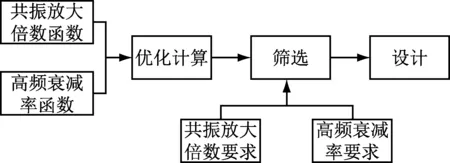
图15 优化流程图Fig.15 Flowchart for optimization

(1) 确定目标函数

根据三参数隔振系统的力学模型，推导目标函数，目标函数为共振放大系数和高频衰减率。由于目标函数的形式较为复杂，文中未给出具体的表达式；

(2) 优化计算

采用带精英策略的非支配排序遗传算法进行优化计算，设置种群数量以及其他参数，经过计算，会得到Pareto最优解，这些最优解可以作为设计参数进行备选；

(3) 筛选

根据指标要求，在Pareto最优解中筛选出满足指标要求的解，经过筛选，确定最终待采用的设计参数；

(4) 优化设计

根据筛选出来的满足指标要求的解，可以得到刚度比以及阻尼比等参数，从而为下一步设计提供依据进行优化计算时需要先得到目标函数。这里的目标函数定义为共振峰以及高频衰减率，可以表示为

(19)

式中：f1，f2分别为共振峰值函数与高频衰减率函数；α，β是决策变量，可以对α，β的取值范围加以限制，这里需要注意的是，α是刚度比的函数，而刚度比大于等于零，因此，α≥1

(20)

式中：αu，αl为α取值的上下限；βu，βl为β取值的上下限。

考虑到α是刚度比的函数，而一般情况下，刚度比不能过大， 对于正弦激励来说，其传递率可以表示为

(21)

共振时的频率比为Ω0，则共振峰值函数可以写成

(22)

为了得到共振频率，需要将传递率求极值，即

(23)

显然Ω0=Ω0(α,β)，将其代回式(22)即可得到共振峰值函数关于α，β的函数，对于高频处的衰减率可以表示为

(24)

式中：Ωh为高频处的频率比。由于表达式较为复杂，文中未给出具体形式。可以借助Matlab符号计算功能来进行推导。

优化计算之后会产生一系列最优解，需要在这些最优解中筛选出符合指标要求的解，这些解对应的α，β即可用来进行进一步设计。

4.2 单位阶跃激励下的参数设计

对于单位阶跃激励来说，由于函数形式较为复杂，无法给出目标函数的显式表达式，这里采用估算法对其动态性能进行估算，然后得出目标函数的近似表达式。以含有一对共轭极点和实数极点的情况为例。

三参数系统的闭环传递函数为

(25)

以一对共轭复根为例，S2，S3共轭闭环主导极点，S1是实数极点。

S1=c，S2,3=a±bj

根据闭环主导极点可以得到系统在单位阶跃输入作用下，输出的拉氏变换时近似表达式为

(26)

式中：M(S)，D(S)分别为(式子)的分子和分母，通过拉氏反变换，系统阶跃响应的近似表达式为

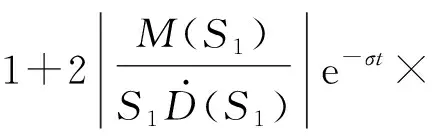
(27)

通过对上式求导数可以，并令其等于0，可以得到峰值时间

(28)

式中：ψ1=arctan(|b/(z0-a)|)；θ3=arctan(|b/(c-a)|)

根据阶跃响应表达式，对于调节时间的估计有

(误差带选择5%)

式中：Z0为零点；S1，S3为极点。

首先根据指标需求确定调节时间的取值，误差带选择为，由于

σ=|a|

故

(29)

(30)

首先可以确定调节时间，调节时间确定以后，即可以确定 的值，然后可以通过根轨迹来选择满足要求的特征根，特征根选定以后，即可以写出传递函数的具体表达式，进而可以通过Laplace逆变换来求出时域响应。

三参数系统的闭环传递函数为

(31)

由于特征根的形式为S1=c，S2=a+bi，S3=a-bi代入到(31)中有

Φ(S)=

(32)

可以得到

(33)

(34)

通过上式可知，只要知道了特征根的分布即可以写出传递函数表达式，进而求出α，β的值，得到时域响应历程。

5 算例仿真

(1) 设计某基于三参数模型的隔振系统，要求共振放大倍数小于3，高频衰减率小于0.01。

表2中是优化后筛选出来的满足共振放大倍数小于3，高频衰减率小于0.01的设计参数值。通过设定优化参数，可以获得不同数量的满足设计指标要求的设计参数。根据设计参数中α和β值，按照前面式(10)和式(11)就可以求出刚度比N和阻尼比ζ，从而指导进行下一步设计。由于表1中满足条件的设计参数较多，选取前5组出来进行分析，可以求得前5组参数的共振频率点，如表3所示。

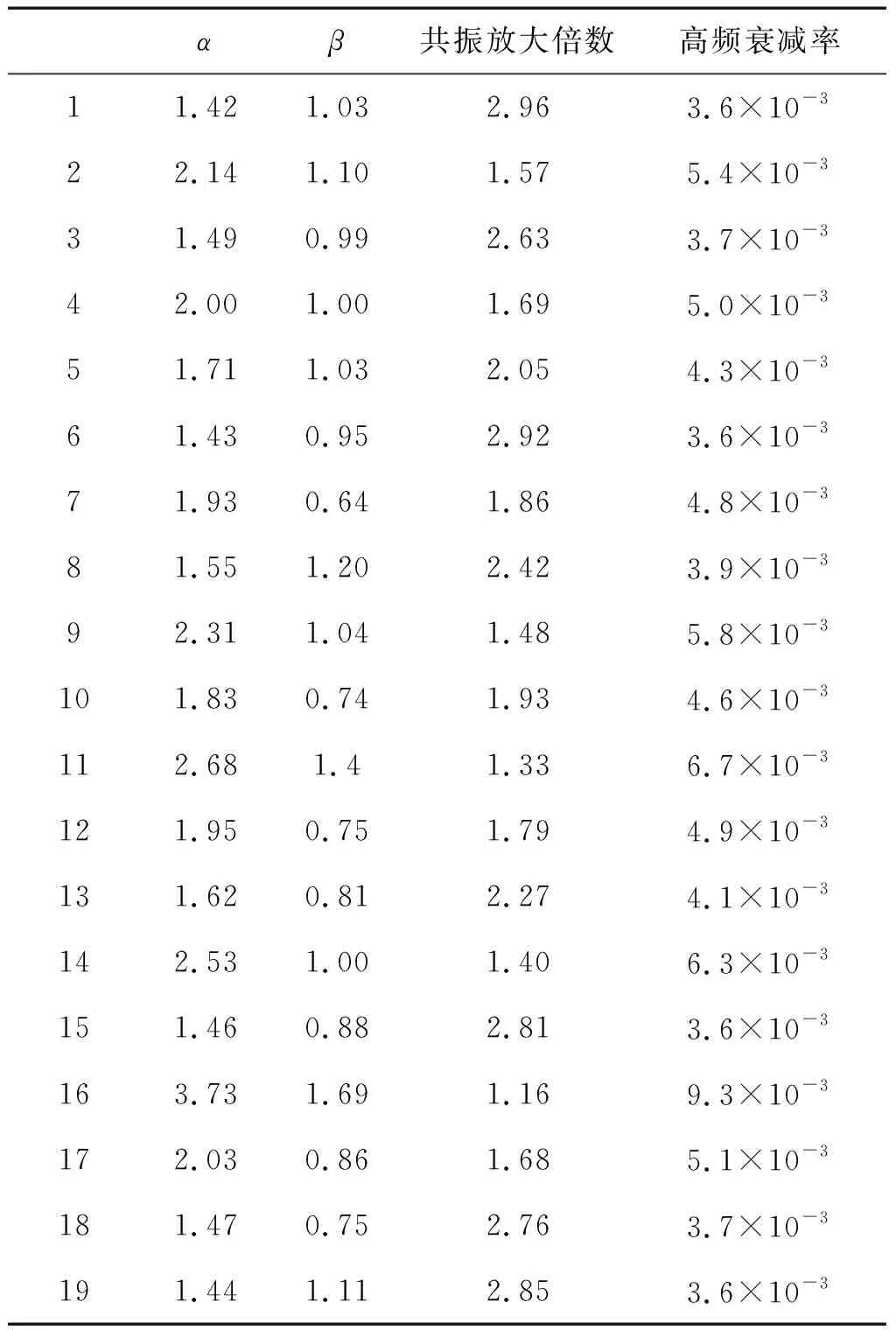
表2 满足指标要求的设计参数Tab.2 Design parameters for requirements

表3 前5组参数的共振频率点Tab.3 Frequency of resonance peak

给出这5组数据的图，即传递率曲线图16是通过NSGA-II算法得到的Pareto前沿，横轴为共振放大倍数，纵轴为高频衰减率。注意衰减率单位一般用dB来表示，这里直接用的是小数，将其取对数乘以20就可以得到以dB表示的衰减率。可以从得到的Pareto前沿数据中挑选出共振放大倍数和高频衰减率均满足要求的参数。图17是通过NSGA-II算法计算得到的Pareto集。横轴为参数α，纵轴为参数β。图16中Pareto前沿和图18中Pareto集相对应。即给定的一组共振放大倍数和高频衰减率对应一组参数α和参数β。筛选图16中满足条件的参数，对应的可以得到相应的α和β的值。图18是这5组参数的传递率曲线。可以看到5组参数得到的传递率曲线，其共振放大倍数均小于3，频率比为20处，衰减率均小于0.01也即-40 dB。不同设计参数时，高频段的传递率也不同。

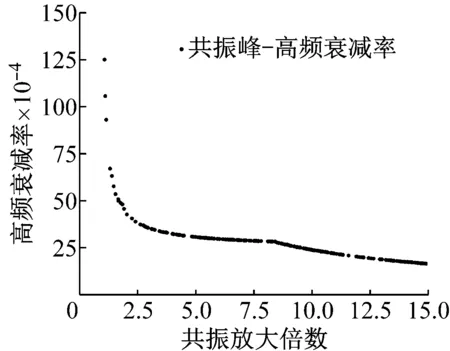
图16 Pareto前沿Fig.16 Pareto front

图17 Pareto集Fig.17 Pareto solution

图18 传递率曲线Fig.18 Transmissibility curve

图19是在共振频率时，系统的时域响应，依然对应的是这5组参数。黑色实线对应的是输入曲线。从图中可以看到，第1组参数对应的时域响应稳态振幅具有最大值，这和图18中的第1组参数的共振放大倍数相对应。第2组参数对应的时域响应稳态振幅具有最小值，这也和图18中第2组参数的共振放大倍数相对应。以此类推，图19中每组参数的时域响应稳态振幅均和图18中共振放大倍数相对应。图19是高频处的时域响应图，也对应了5组参数。可以看到初始时曲线震荡较为明显。图21是高频时域响应的放大图，第1组参数对应的稳态振幅最小，这和图18中的传递第1组参数具有最大的衰减率相对应，其他每组参数的时域稳态振幅均和图18中的相对应。

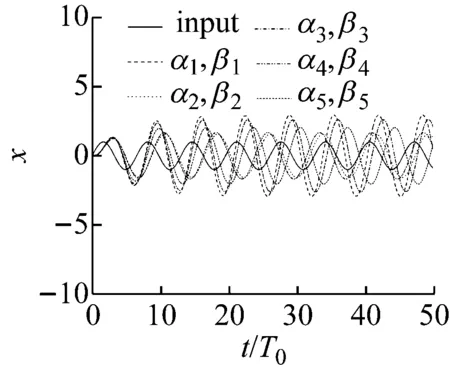
图19 共振峰处的响应Fig.19 Response at resonance peak

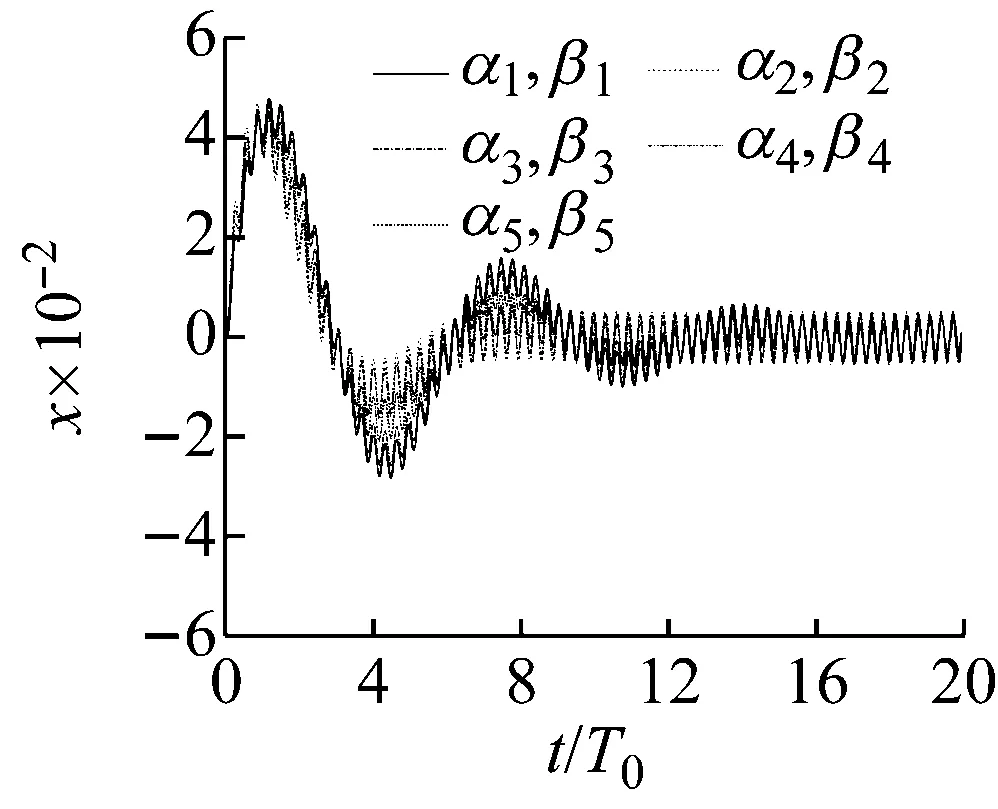
图20 高频处的响应Fig.20 Response in the high frequency domain

图21 高频处的响应(放大图)Fig.21 Response in the high frequency domain (larger version)

(2)要求系统在单位阶跃激励作用下，调节时间为20以内。

根据指标要求可以确定

因此要在特征根里面筛选出满足a<-0.2的根，由于要满足主导极点的要求，可进行进一步的筛选，筛选出来满足条件的参数。

图22是峰值时间的估算值和解析值的比较。需要注意的是，这里的峰值时间指的是归一化的时间。可以看到，两者吻合良好，说明估算值是可信的。图23时调节时间的比较，依然是归一化的时间。当β较小时，两者吻合非常好，而当β增大时，部分值误差加大，但也在7%以内，并且调节时间满足指标要求的控制在20以内。图24是超调量的比较，当β取值较小时，两者吻合良好，当β增大时，误差增大，但控制在7%以内。

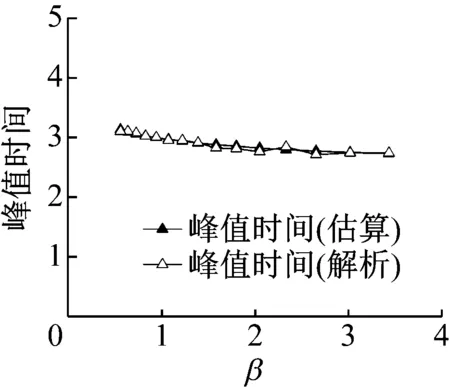
图22 峰值时间对比Fig.22 Comparison of peak time

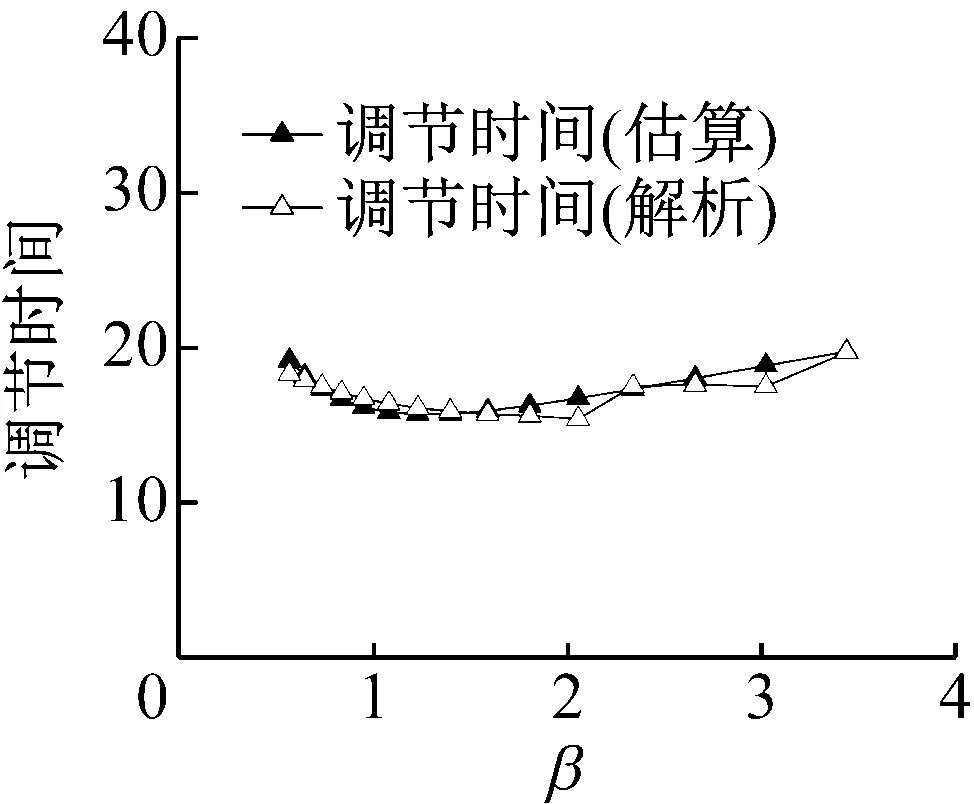
图23 调节时间对比Fig.23 Comparison of settling time

图24 超调量对比Fig.24 Comparison of overshoot

6 结 论

采用归一化参数模型对三参数隔振系统的动力学特性进行了分析，建立了归一化参数与物理参数刚度比以及阻尼比的对应关系，针对正弦激励以及单位阶跃激励下三参数隔振系统，采用归一化模型对其时域响应进行分析，给出了其时域响应的解析表达式，最后对三参数隔振系统进行了参数优化，主要结论如下：

(1) 归一化的参数模型可以从时域和频域两个角度对三参数隔振系统进行分析，且形式简单，易于分析。

(2) 采用多目标优化方法对正弦激励下三参数隔振系统的进行参数优化，经参数优化后，可以同时保证共振峰以及高频衰减率满足指标要求。

(3) 利用估算方法对单位阶跃激励下的三参数隔振系统进行参数设计，相比于解析方法来说可以大幅减少运算量，并且误差小于7%，仿真算例验证了方法的可行性。