基于水击防护的球阀关闭规律研究
彭利坤, 屈 铎, 许文奇, 陈 佳
(海军工程大学 动力工程学院,武汉 430033)
大型舰船、潜艇上常设有纵倾均衡调水系统以调节舰船首尾平衡,其管系中的电液球阀启闭规律无法进行精确控制,而输水过程中球阀突然关闭时会产生剧烈的水击现象[1],不仅导致管系的振动噪声,甚至可能造成管路破裂、阀门等设备损坏。
针对突然关阀、停泵等引起的流体管路水击问题,王福军等采用基于特征线法的热流体仿真平台Flowmaster对某泵站进行水力过渡过程计算,并对泵后阀门关闭规律和空气阀布置方案进行优化[2];由于特征线法难以考虑管道空间效应等局限性[3],CFD(Computational Fluid Dynamics)逐渐被应用于水击压强计算[4-5]。Nikpour等[6]采用标准k-ε湍流模型模拟水击现象,得到了与实验数据基本一致的结果。张飞等[7]采用短时傅里叶变换方法,研究了水泵水轮发电机组球阀动水关闭前、后及过程中机组及球阀的主要频率成分变化情况。对于典型的球阀控制流体管路系统,因舰船空间狭小,单相调压水箱、蓄能器等传统的水击防护措施不易在舰船上实施,蔡标华[8]采用AMEsim对舰船首尾移水系统进行仿真与实验分析,认为延长球阀关闭时长能有效抑制水击;郭兰兰等[9-10]采用FLUENT滑移网格技术对球阀关闭水击压强进行计算,认为相比匀速、匀加速关阀方式,无阀腔球阀模型的匀减速关阀方式对水击现象的抑制效果较好。在液压泵站过渡过程中常采用两阶段关闭液压阀进行水击防护,并取得了较好的效果[11]。然而,对于球阀控制流体管路的水击防护,仅有“快开(阀)慢关(阀)”、“先快后慢关阀”[12]等定性分析,尤其是两阶段线性关阀具体控制规律的水击防护研究尚未见报道。因此,以舰船均衡调水系统为原型,搭建了具有双向调水功能的实验系统,通过CFD数值模拟与实验研究相结合的方法,重点分析了先快后慢的两阶段线性关阀的水击防护效果,对球阀关闭规律进行优化,以期为球阀关闭时低噪声控制提供指导。
1 CFD水击压强计算
1.1 实验系统简介
实验系统原理如图1所示,通过控制空气瓶内压缩空气的压力来控制调水的速度;通过控制空气瓶内空气的输送方向实现双向调水;其中管路1、管路2分别安装数字步进球阀Va(最快启闭时间3 s,即启闭最大速度30 °/s)、电液球阀Vb(启闭时间约0.5 s)。根据相似性原理和实验室具体情况搭建的实验系统台架如图2所示。

图1 实验系统原理示意图Fig.1 Schematic of experimental system

图2 实验系统整体实物图Fig.2 Physical map of experimental system
实验系统中的数字球阀和电液球阀仅驱动装置不同,与流场接触的内部结构基本相同,如图3所示,阀芯外壁与阀体内壁构成了阀腔。
1.2 数值模拟方法
由球阀阀芯球体、阀腔、阀芯通道的几何关系,构建球阀一定开度下时的剖面与阀口投影示意图如图4所示,推导得到球阀流通面积A与开度θ的关系
(1)
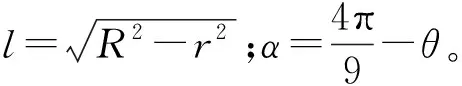
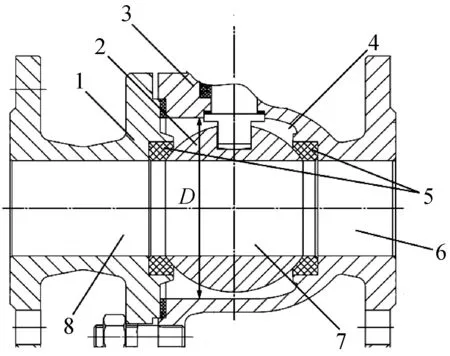
1-左阀体;2-阀芯;3-右阀体;4-阀腔;5-密封圈;6-进口管道;7-阀芯通道;8-出口管道

(a)
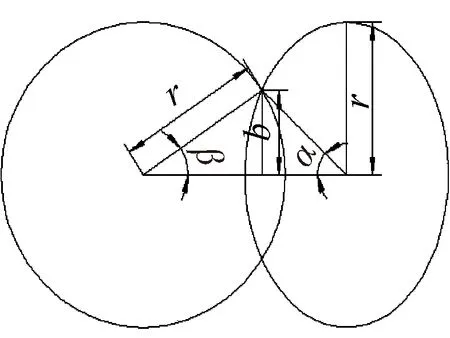
(b)图4 球阀剖面与阀口投影示意图Fig.4 Cutaway view and projection drawing of valve
根据实验系统实际管长,取阀前管长l1、阀后管长l2建立球阀全开时的流场几何模型,同时针对球阀结构与运动特点,将整个流域分为进口管路、阀芯通道、阀腔和出口管路四部分建模。采用结构化网格对模型进行网格划分。
首先对网格模型进行了网格无关性模拟。针对0.5 s时长单线性匀速关阀工况,在20万网格的基础上,每次增加2万网格对其进行仿真,结果发现,当网格增加到约28万时,其最大水击压强的计算结果与网格约为26.2万的计算结果相差仅为0.3%,所以采用约26.2万的网格模型。该模型网格质量在0.3以上,并对运动边界进行了适当加密,其网格如图5所示。
根据调水系统的工况,调水时两端水箱的压差为4 bar,其中一端与空气瓶连通,而另一端连通大气,因此,设置参考压力为1 bar,进口设置为总压4 bar的压力进口;出口设置为0 bar的压力出口。采用FLUENT滑移网格技术和标准k-ε湍流模型模拟球阀关闭瞬态过程,同时定义交界面以便各流域进行数据交换,并通过UDF(User Defined Function)实现对阀芯运动规律的精确控制。
(a)阀芯通道及进出口管路

(b)阀腔图5 几何模型网格Fig.5 Mesh of geometrical model
球阀由全开到完全闭合是一个动态过程,管道中流体为非稳态湍流流动,其连续性方程和动量方程为
(2)
(3)
CFD计算时采用标准k-ε湍流模型来使上述方程封闭。
1.3 数值计算结果与实验数据对比
根据实验系统特性对模型各参数选取如表1所示。
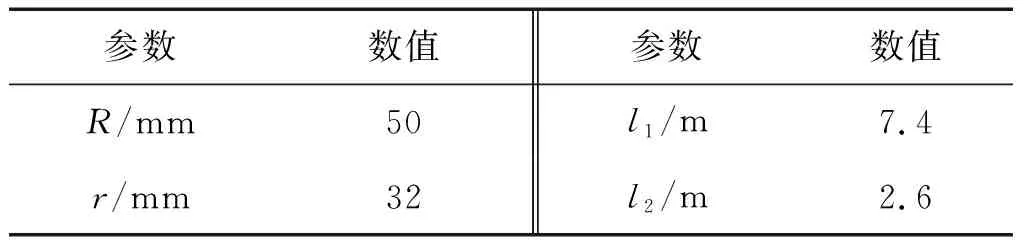
表1 模型参数Tab.1 Parameters of model
对球阀关闭过程进行瞬态数值模拟,监测阀前截面的平均压力,也即水击压强。研究水击问题需考虑水的可压缩性,根据流体体积模量表达式(4)[13]、流体密度ρ的表达式(5)及水击波波速c的表达式(6),在Fluent中采用UDF定义三者之间的联系以考虑水的可压缩性。
(4)
(5)
(6)
式中:K为水的体积模量;V为水的体积;p为压强。
以0.5 s时长匀速关闭电液球阀工况的水击压强数值计算结果与实验结果对比如图6所示。
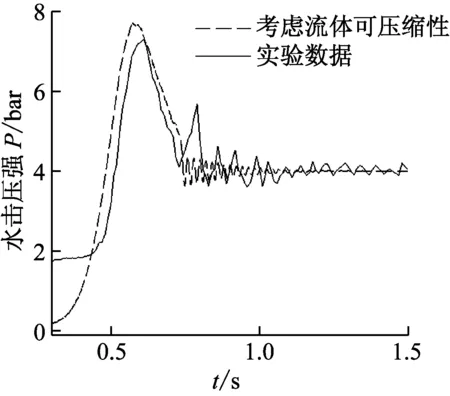
图6 水击压强计算值与电液球阀实验值对比Fig.6 Water hammer pressure of experiment and simulation
从图6中可知,实验得到的最大水击压强为7.31 bar,计算所得的最大水击压强为7.722 bar,就最大水击压强而言,计算值与实验值误差为5.64%。仿真采用单线性匀速关阀;实验中电液球阀动作是电磁阀打开、液压推动阀芯旋转关闭的,加速阶段很短,可近似看作匀速关阀。实验和数值模拟中关阀规律上存在的这点不同是造成误差的主要原因之一。数值模拟的水击压强在阀门完全关闭后先上下波动,最后稳定在4 bar,这与实验结果吻合较好,说明考虑水的可压缩性进行关阀水击现象的数值模拟是可行的。
1.4 CFD计算结果分析
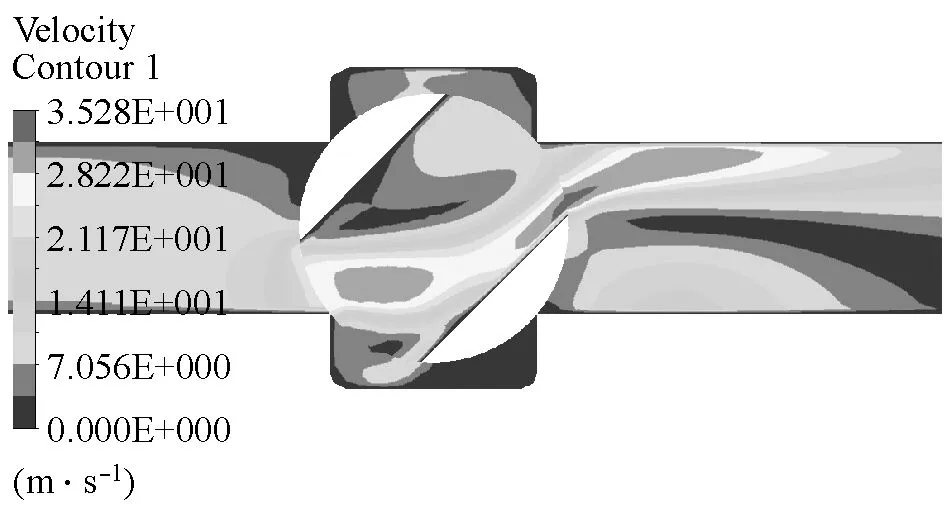
对于实验系统中的球阀,由式(1)可知,当阀芯由全开旋转80°时,球阀恰好完全关闭。对实验系统球阀管路模型在有效关阀时长内采用先快后慢的两阶段线性关阀进行CFD数值仿真,且本节中数值模拟的所有工况中整个关阀(球阀阀芯从全开旋转90°)时长均采用0.5 s。其中,“以270 °/s速度快关43.75%”工况的球阀模型纵截面各时刻的压力云图和速度云图分别如图7、图8所示。从图7和图8中可以看出,球阀阀芯在由全开到关闭的过程中,由于阀芯的节流作用,流速发生了剧烈的变化,造成了严重的压力损失,而且进口管道和出口管道的压差会随着球阀的关闭而增大。

(a)0.4 s
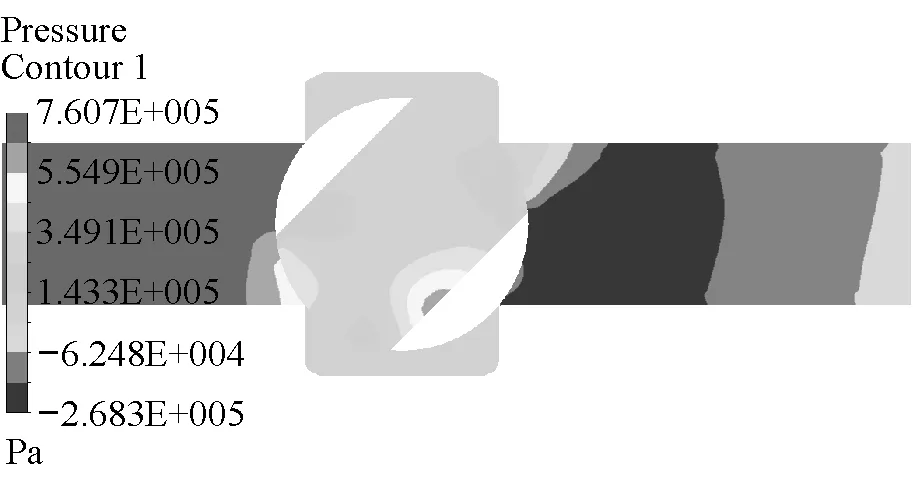
(b)0.5 s

(c)0.6 s

(d)0.7 s图7 各时刻压力云图Fig.7 Pressure contour at different time
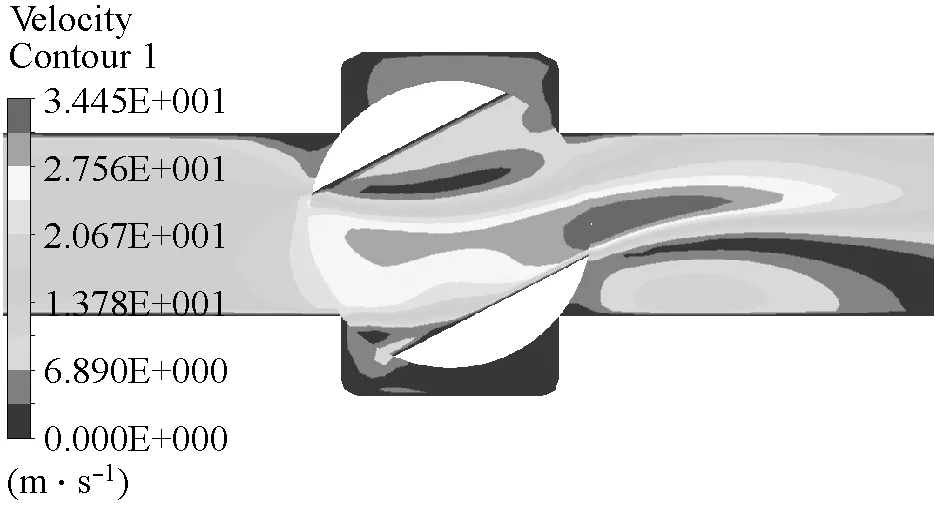
(a)0.4 s
(b)0.5 s

(c)0.6 s
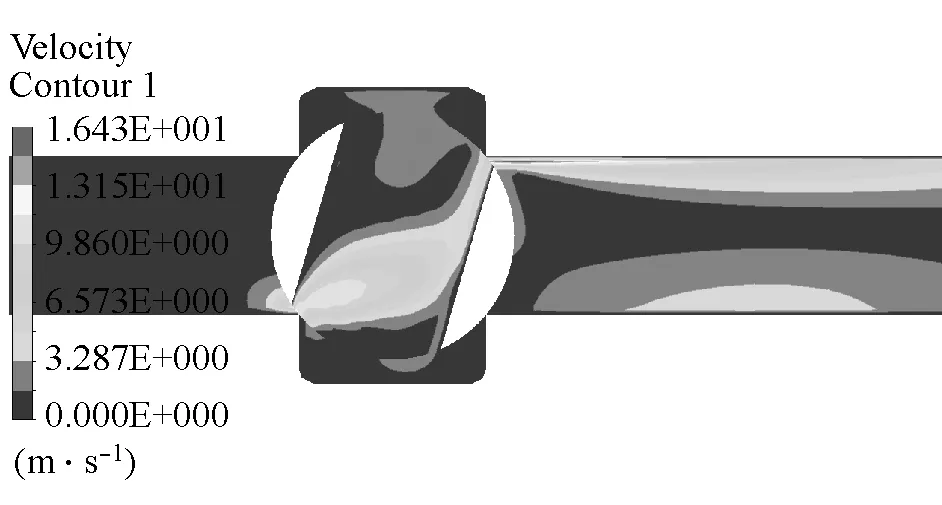
(d)0.7 s图8 各时刻速度云图Fig.8 Velocity contour at different time
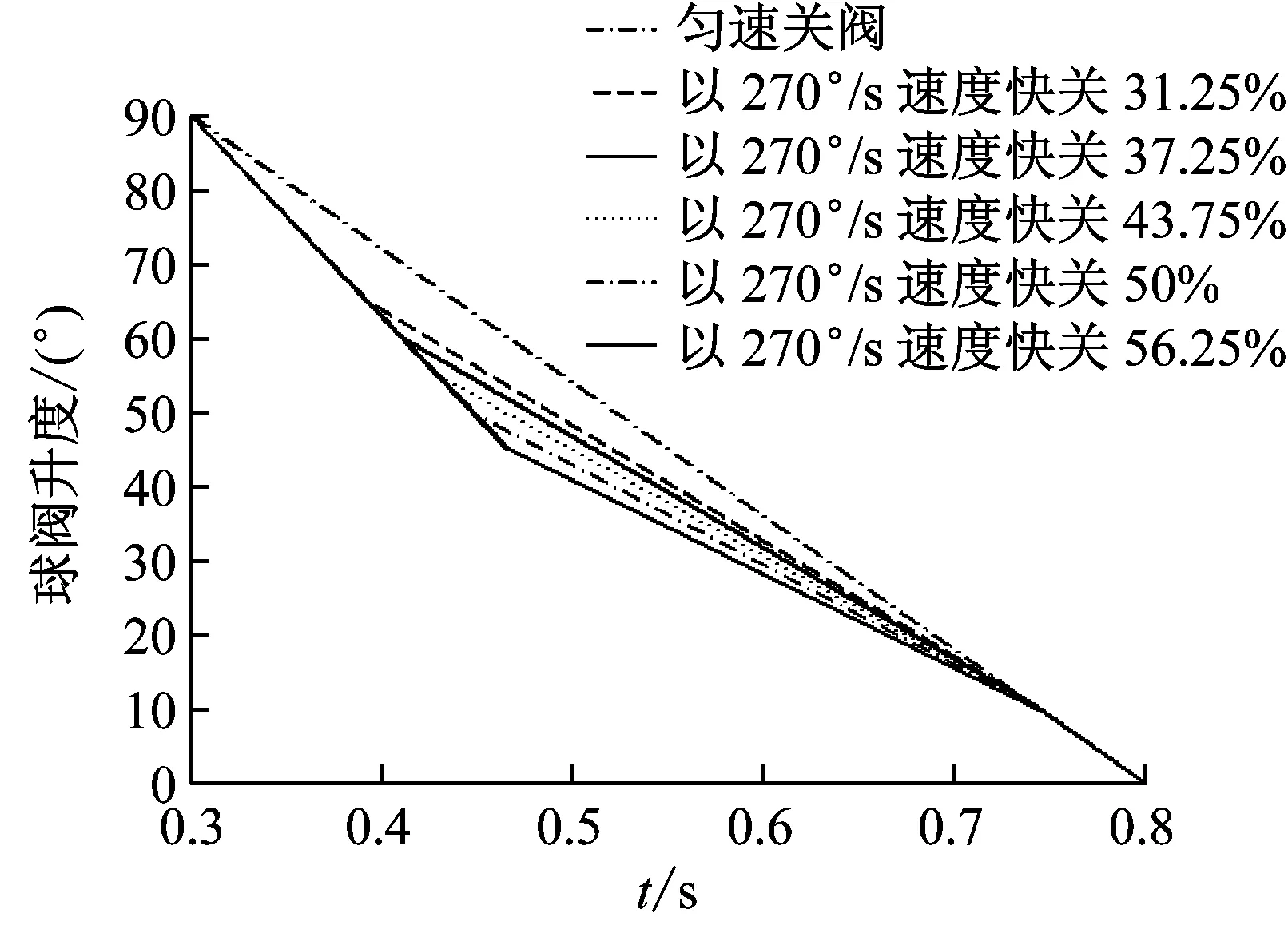
图9 快关阶段角度不同的关阀规律Fig.9 Closing law with different angle at quick-closing stage
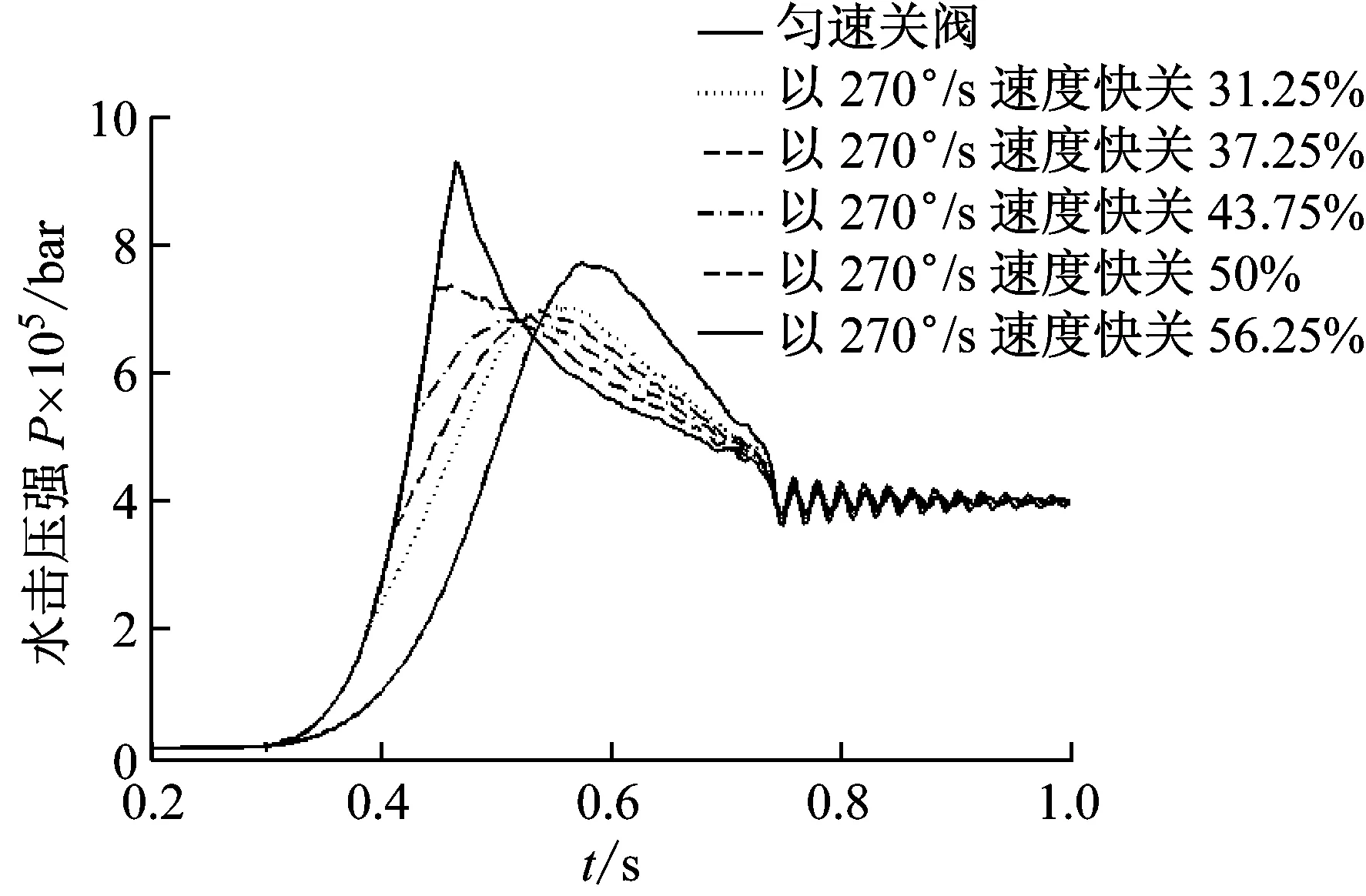
图10 快关阶段角度不同时水击压强曲线Fig.10 Water hammer pressure of different closing law with different angle at quick-closing stage
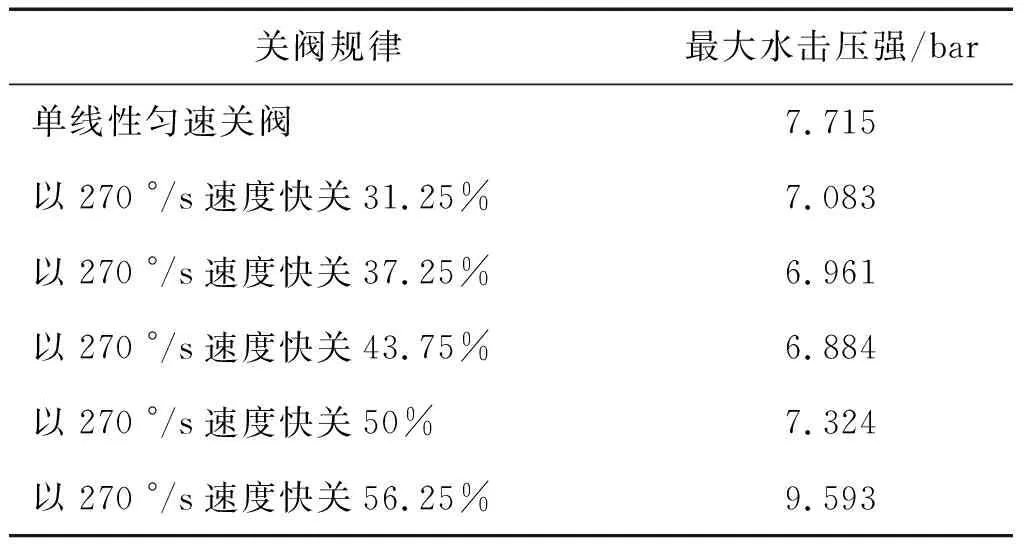
表2 快关阶段角度不同时的最大水击压强Tab.2 Maximum pressure of different closing law with different angle at quick-closing stage
快关阶段速度均为270 °/s、快关阶段角度不同的关阀规律如图9所示,其对应的水击压强曲线如图10所示,其最大水击压强如表2所示。从图10和表2可知:
(1)采用先快后慢的两阶段线性关阀时,阀门完全关闭后的压力振荡较匀速关阀时有了明显改善;
(2)较线性关阀而言,采用先快后慢的两阶段线性规律进行关阀时,水击压强峰值将提前出现,当快关阶段角度太大时,反而导致水击压强变大,其中“以270 °/s速度快关全角度56.25%”的最大水击压强达到9.593 bar;当快关阶段角度较小时,则对水击的抑制效果不佳,其中“以270 °/s速度快关31.25%”的最大水击压强为7.083 bar;
(3)就本模型而言,关阀时长均为0.5 s时采用“以270 °/s速度快关43.75%”的关阀方式的水击防护效果较好,其最大水击压强仅为6.884 bar。
在上述结果(3)的基础上研究快关角度均为43.75%时快关阶段速度不同工况下的水击压强,具体关阀规律如图11所示,其对应的关阀水击压强如图12所示,不同关阀规律下的最大水击压强如表3所示。
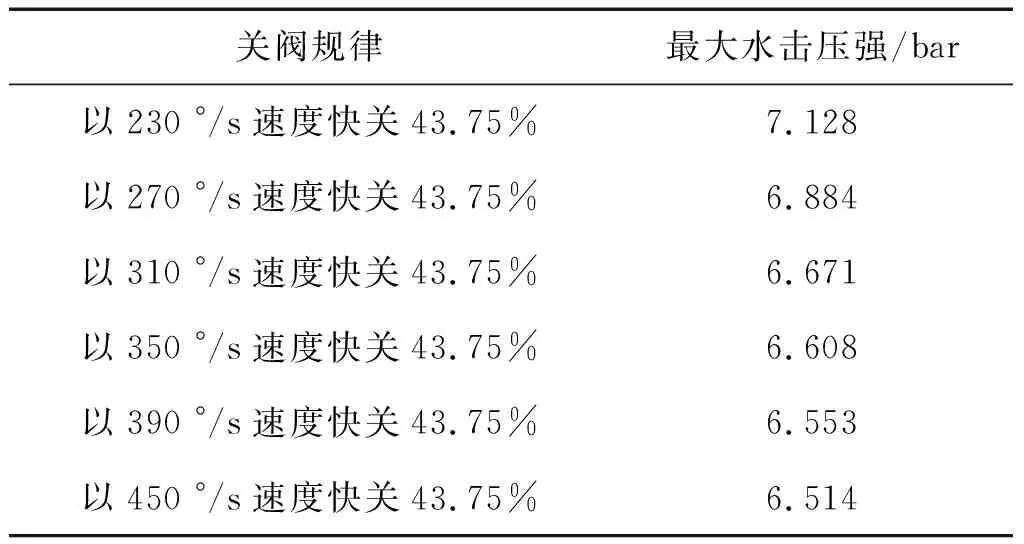
表3 快关阶段速度不同时的最大水击压强Tab.3 Maximum pressure of different closing law with different velocity at quick-closing stage
从图11、图12和表3中可知:快关阶段速度越快,水击压强最大值出现时刻越早;当快关角度均为全行程的43.75%时,最大水击压强随快关阶段速度增加而减小,且其衰减程度变缓。实际应用中关阀速度不可能无限增大。
2 实验结果分析
软件设置了多种两阶段关阀控制规律,其中关阀时长均为4 s的两阶段关阀规律如图13所示,CFD仿真计算的关阀水击压强曲线如图14所示,实验值曲线如图15所示。
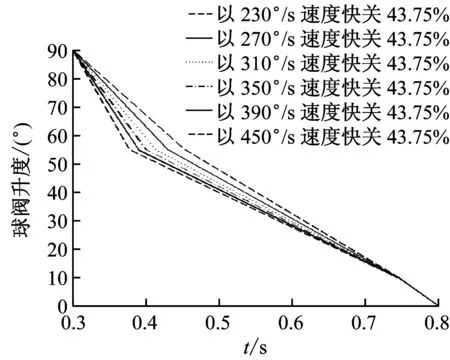
图11 快关阶段速度不同的关阀规律Fig.11 Closing law with different velocity at quick-closing stage

图12 快关速度不同时水击压强曲线Fig.12 Water hammer pressure of different closing law with different velocity at quick-closing stage

图13 两阶段关阀规律Fig.13 Valve-closing law of two stage

图14 不同关阀规律水击压强仿真值Fig.14 Water hammer pressure of different valve-closing law of simulation
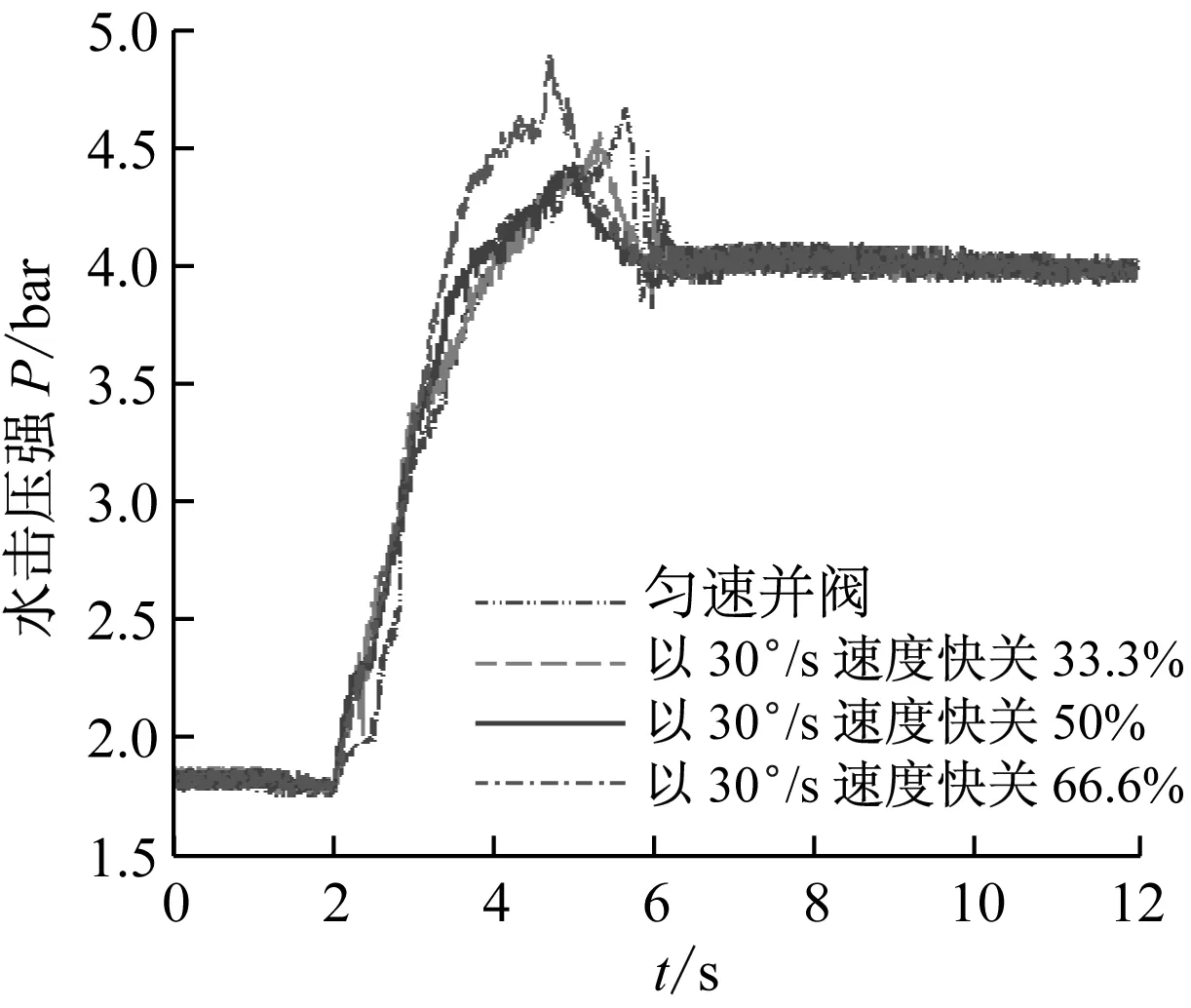
图15 不同两阶段关阀规律的水击压强实验值Fig.15 Water hammer pressure of different valve-closing law of experiment
从图14、图15中可看出,采用先快后慢的两阶段线性关阀规律时,水击压强的峰值出现的时间提前,且阀门完全关闭后的压力振荡明显减小;但如果快关阶段角度太大反而会导致最大水击压强增加,而快关阶段角度太小则造成水击压强抑制效果不佳,以上四种关阀规律中以快慢速比1.33且快关50%时的水击抑制效果最好,这与CFD仿真结论基本一致。
同时将不同关阀规律最大水击压强的实测数据与仿真值对比如表4所示。从中可看出,就最大水击压强而言,仿真值与实验值误差均在6%以内,考虑到调水压力难以精确控制等因素,误差在允许范围内。
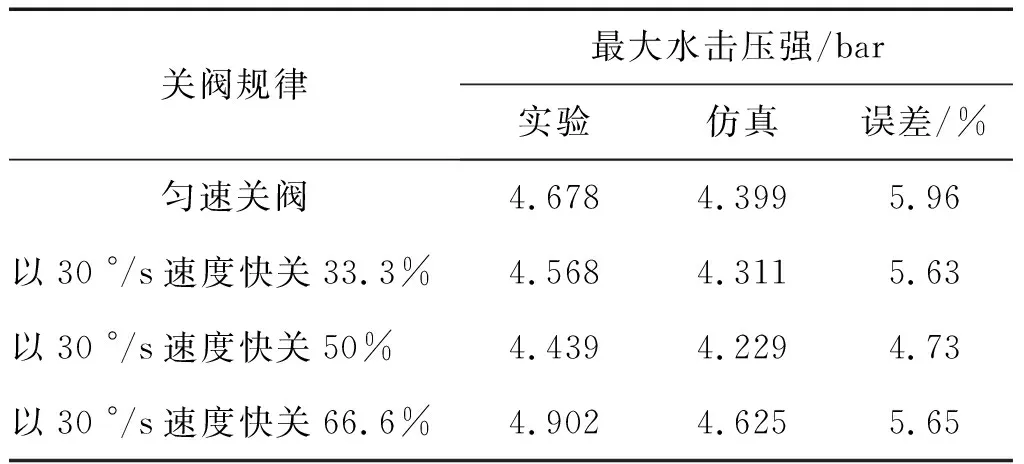
表4 最大水击压强仿真与实验值对比Tab.4 Maximum pressure of experiment and simulation
3 结 论
(1)本文针对舰船纵倾均衡系统中球阀控制流体管路在突然关阀时产生剧烈水击问题,设计搭建了包含开关规律可精确控制数字球阀的实验系统,通过对比实验数据验证了CFD应用于水击计算的可行性。
(2)通过分析CFD计算结果与实验数据可知:当关阀时长一定时,采用先快后慢的两阶段线性关阀能有效抑制球阀关闭后的压力振荡情况,且水击压强峰值出现时刻提前,但是快关阶段角度太大时,反而会增大关阀过程水击压强;而当快关阶段角度较小时,则造成水击压强抑制效果不佳,就本研究而言,以快慢速比1.6左右且快关角度在45%附近时水击防护效果较好。

