任意光滑截面桥墩地震动水压力分析

王丕光， 赵 密， 杜修力

(1.北京工业大学 城市与工程安全减灾教育部重点实验室，北京 100124；2.清华大学 土木工程系，北京 100084)

随着世界经济的发展，各国均投入巨资兴建跨越江海的大跨度深水桥梁工程，我国已经修建的大规模的跨江跨海工程长大桥梁中许多桥梁处于深水之中[1]。这些桥梁工程多数位于地震区，在地震作用下桥墩与周围水体的动力相互作用会对桥墩产生动水压力，研究表明该动水压力会对深水墩柱结构和桥梁结构的动力反应产生较大影响[2-6]。桥梁作为生命线工程，一旦遭受地震破坏将会产生无法估量的后果。因此充分认识地震作用下桥墩与周围水体的动力相互作用，对于新建深水高墩桥梁抗震设计和已建桥梁抗震安全评估具有重要的意义。

实际工程中，存在各种截面形式的墩柱结构，如圆形、矩形、椭圆形和圆端形等。针对圆形桥墩，Tanaka等[7]利用解析法分析了水平地震作用下齐水面弹性圆柱体单位长度上动水压力的附加质量系数和阻尼系数；赖伟等[8]提出了一种圆形桥墩上地震动水压力的半解析半数值方法；Li等[9]提出了圆形空心桥墩上地震动水压力的简化计算公式；黄信等[10-11]讨论了自由表面波、水体压缩性和水底吸收边界对圆形桥墩地震动水压力的影响；杜修力等[12-13]提出了可压缩水体条件下圆形桥墩地震动水压力的时域算法和时域简化公式。另外，刘振宇等[14-15]提出了矩形空心桥墩地震动水压力的计算公式。上述情况表明，目前对于地震作用下圆形和矩形桥墩地震与周围水体的动力相互作用问题已经取得了可供实际应用的研究成果，但还缺乏对椭圆形和圆端形等光滑截面形式桥墩地震动水压力的研究。

本文针对地震作用任意光滑截面形式桥墩与周围水体的动力相互作用问题，基于辐射波浪理论，根据水体控制方程和边界条件，通过分离变量和傅里叶级数展开的方法，推导了任意光滑截面桥墩地震动水压力的解析解。

1 控制方程及边界条件

地震作用下任意光滑截面桥墩与水体动力相互作用的分析模型如图1所示。假定地基为刚性，水体为无旋、无黏、可压缩的小扰动流体。柱坐标系原点设于墩底并以x轴正方向为θ=0°方向，桥墩表面方程为r=a(θ)，桥墩高度为H，水深为h。地面运动沿x方向的位移为ug，桥墩的弹性位移为us，桥墩的绝对位移为u=ug+us。柱坐标系下，以动水压力p作为未知量的水体控制方程为

(1)

式中:c为声波在水中的传播速度，不可压缩水体条件下1/c=0。初始时刻，水体静止。

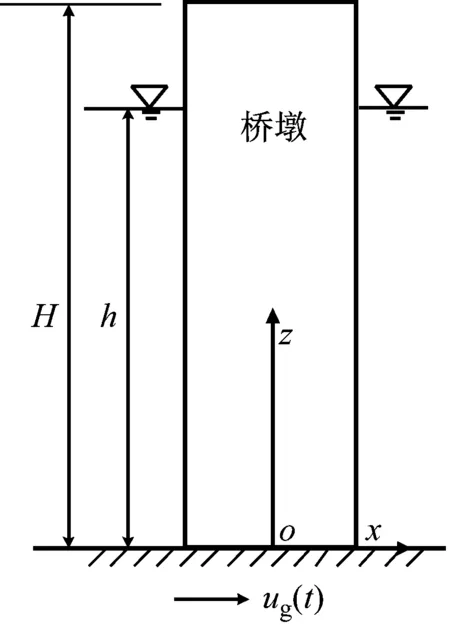
图1 水中任意光滑截面桥墩分析模型Fig.1 Definition of the problem

水体底部、静水表面、无穷远以及水体与结构交界面边界条件为

(2)

p=0z=h

(3)

p=0r→∞

(4)

(5)

式中:n为柱体表面任意点的单位外法线向量;α为n与x轴方向的夹角，则

(6)

2 动水压力的频域解

地面简谐运动时水体的动水压力和桥墩的绝对位移可以表示为

p(r,θ,z,t)=P(r,θ,z)eiωt

(7)

u(z,t)=Ueiωt=(Us+Ug)eiωt

(8)

式中:ω为结构的振动频率;Us和Ug分别为频域下结构的弹性位移和刚体位移。柱坐标系下，P(r,θ,z)可分离变量为

P=R(r)Θ(θ)Z(z)

(9)

将式(7)代入控制方程式(1)，可得到三个解耦的方程

Θ″+n2Θ=0

(10)

Z″+λ2Z=0

(11)

(12)

式中:n和λ为待定系数。根据边界条件式(2)～式(4)，可得到桥墩动水压力P的表达式为

(13)

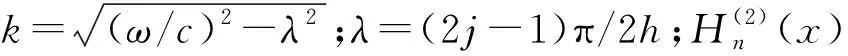
将式(13)代入边界条件式(5)并整理得

(14)

其中,

(15)

(16)

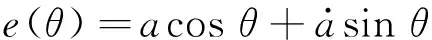
(17)

将式(14)等式两边同时乘以cosλz，并在区间[0,h]积分，利用特征函数cosλz的正交性可得

(18)

其中,

(19)

基于本文桥墩表面连续光滑的假定，可将函数e(θ),qjn(θ)和gjn(θ)展开成傅里叶级数的形式。e(θ),qjn(θ)和gjn(θ)傅里叶级数展开式分别为

(20)

(21)

(22)

将式(20)～式(22)代入式(18)整理得

⋮

(23)

式(23)可重写为如下矩阵的形式

NC=J

(24)

其中,

J={a0,b0,a1,b1,…}T

(25)

(26)

(27)

C=N-1J

(28)

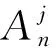
3 动水力及运动方程

地震作用下桥墩表面沿单位高度上的水平动水力为

(29)

将式(13)代入式(29)整理得

F(z)=Fg+Fs

(30)

(31)

(32)

(33)

式中:Fg和Fs分别为地震作用下桥墩刚体运动和弹性运动引起的动水力。

假定桥墩为弯曲悬臂梁，将桥墩的弹性位移Us按无水振型展开为

(34)

式中:Xi(z)为桥墩的第i阶振型；Yi(ω)为第i阶振型坐标，地震作用下可按如下方程求解

-ω2MiYi(ω)+iωCiYi(ω)+KiYi(ω)=ω2UgDi+Fi

(35)

其中,

(36)

(37)

Ci=2ζiωiMi

(38)

(39)

(40)

式中:A为截面面积;ρs为桥墩质量密度；ωi为第i振型对应的自振频率;ζi为相应的阻尼比。

将式(31)和式(32)代入式(40)整理得

(41)

(42)

(43)

将式(37)、式(38)和式(41)代入式(35)整理得

(44)

将式(44)代入式(34)，通过傅里叶反变换可得到时域下桥墩的弹性位移为

(45)

4 数值算例

算例1旨在通过对刚性桥墩动水压力的分析以验证本文提出的任意光滑截面桥墩动水压力计算方法的精度。分别通过本文方法和ABAQUS声固耦合方法计算单位脉冲运动作用下刚性椭圆形和圆端形桥墩的动水力；对式(31)进行傅里叶反变换可得到刚性桥墩动水力的时域解。图2是结构刚体运动位移，脉冲持时0.2 s，频谱覆盖了地震作用频段；图3为算例中桥墩的截面尺寸，图中L1和L2的值分别取为20 m和30 m；水深取为80 m，水体声速和密度分别为1 438 m/s2和1 000 kg/m3。

(a)时程

(b)傅里叶谱幅值图2 刚性桥墩位移时程和傅氏谱Fig.2 The time history of displacement of rigid pier and its Fourier spectrum

图3 桥墩模型截面尺寸Fig.3 Cross-section of the piers

图4为桥墩截面函数e(θ)的傅里叶级数展开解与精确解的比较；由图中可以看出，精确解与傅里叶展开解吻合很好。可见，桥墩表面连续光滑函数的傅里叶级数展开具有很高的精度。图5为沿桥墩高度积分的总动水力的本文方法与ABAQUS声固耦合方法的比较；由图中可以看出，两种方法计算得到的结果一致；可见，本文方法具有很高的精度，并且避免了求解复杂的流体动力问题。

(a)模型1

(b)模型2

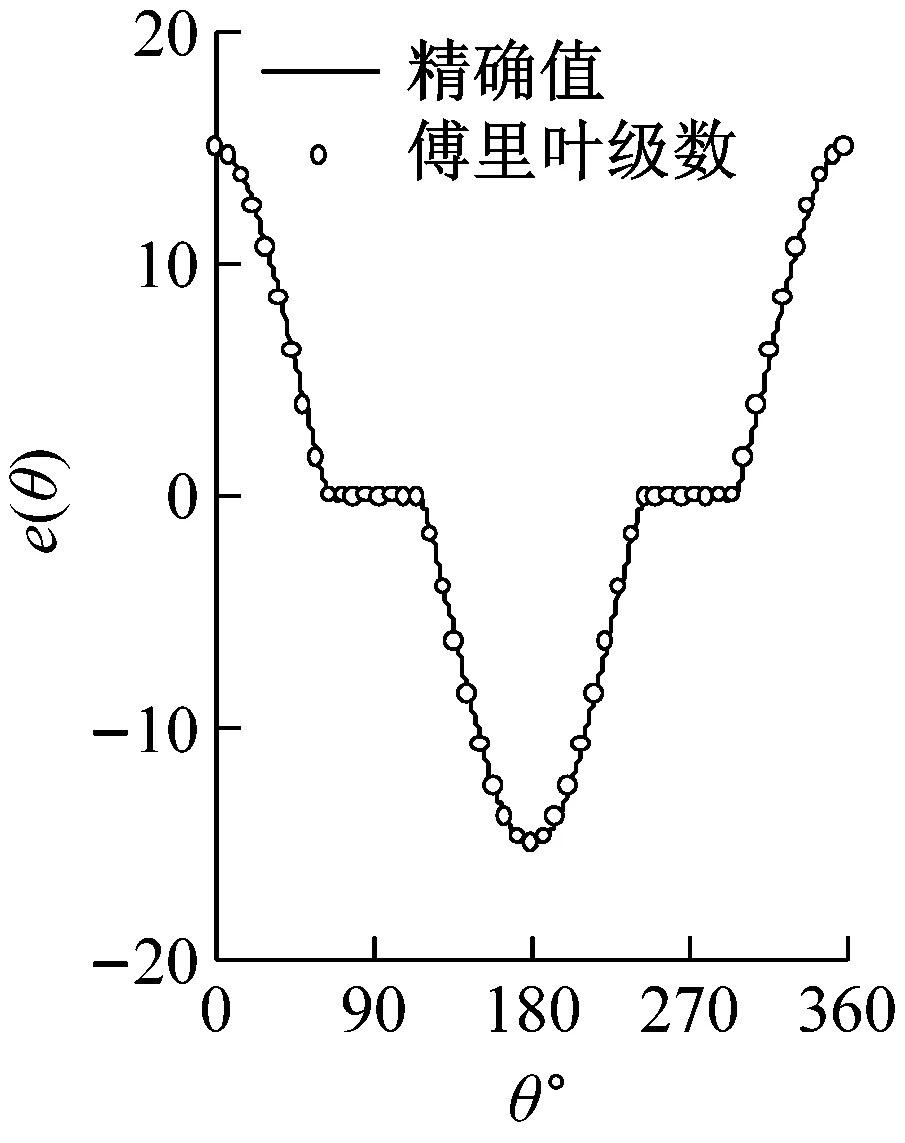
(c)模型3

(d)模型4图4 函数e(θ)的傅里叶级数展开Fig.4 Fourier expansion of the function e(θ)

(a)模型1

(b)模型2

(c)模型3

(d)模型4图5 桥墩总动水力时程Fig.5 The time history of total hydrodynamic force on piers

(a)

(b)图6 El-Centro地震波加速度时程和傅氏谱Fig.6 The time history of acceleration of El-Centro wave and its Fourier spectrum

(b) 模型4图7 动水力振型系数和Fig.7 The mode correlation coefficients and for the hydrodynamic force on the pier

5 结 论

本文基于流体辐射波浪理论，通过分离变量和将光滑连续函数展开成傅里叶级数的方法，推导了一种任意光滑截面桥墩地震动水压力的解析公式，并基于弯曲悬臂梁模型给出了任意光滑截面桥墩动力反应的求解方法。刚性桥墩的结果表明，采用本文解析公式计算的桥墩地震动水压力与声固耦合数值方法的计算结果吻合很好，证明了任意光滑截面桥墩地震动水压力解析公式的正确性。弹性桥墩的结果表明，地震动水压力增大了桥墩的动力反应，并且水深与桥墩高度的比值是决定动水压力影响大小的一个主要因素；当比值较大时动水压力对桥墩地震反应影响较大，不可忽略，这一点在深水桥梁的设计中必须注意。

(a) 模型2

(b) 模型4图8 墩顶位移时程Fig.8 The time history of displacement on top of the pier

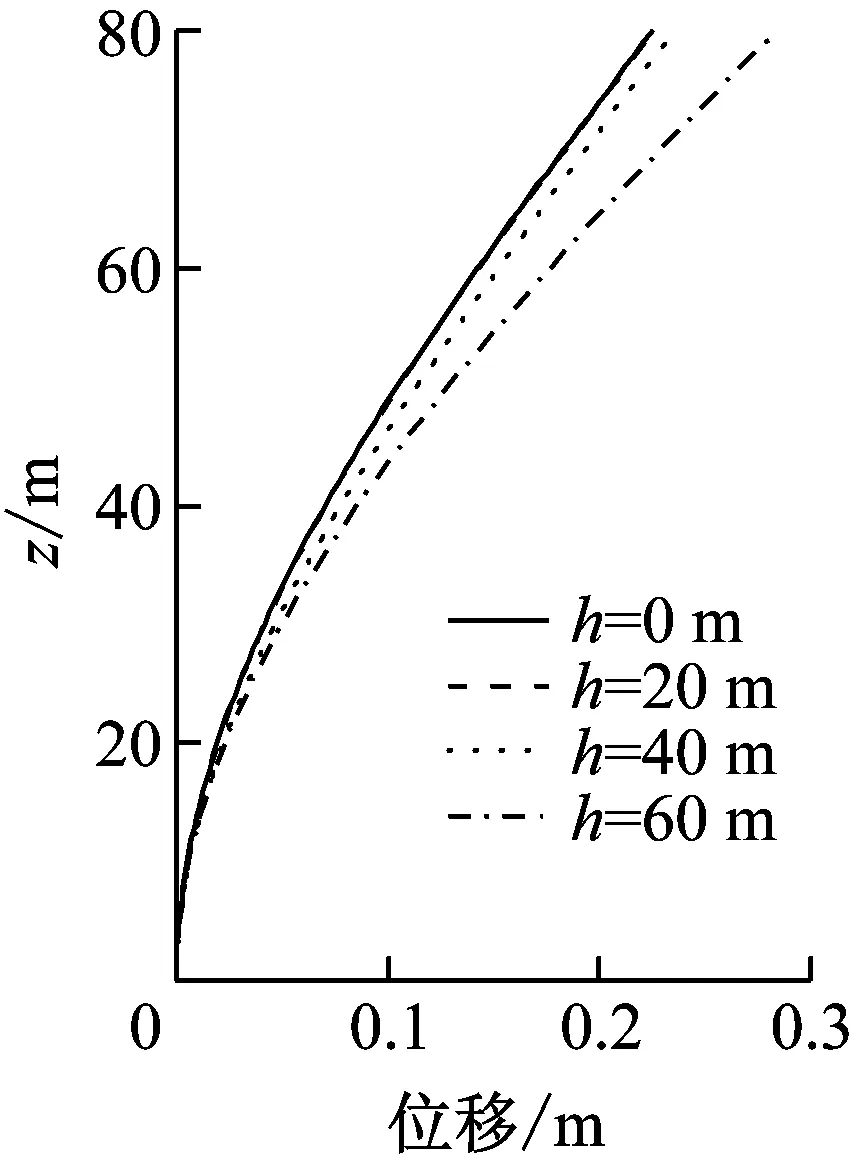
(a) 模型2

(b) 模型4图9 墩身峰值位移Fig.9 Peak displacement along the vertical direction